Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ

Методические указания

 по выполнению контрольных работ для студентов заочной формы обучения, обучающихся  по направлению 380301 Экономика

 

 

Санкт-Петербург

2017

УДК

 

Рассмотрено и рекомендовано к изданию Методическим советом

Института экономики, менеджмента и информационных технологий

(протокол № _____ от «___» __________ 2017 г.)

 

Составители:

кандидат технических наук С.Е. Пономарев

Рецензент

доцент кафедры Информационных технологий и математики СПбУТУиЭ

кандидат технических наук Е.Е. Майоров

0-64  Методы оптимальных решений: методические указания по выполнению контрольных работ для студентов заочной формы обучения / сост. В.В. Курлов, ун-т технол. упр. и экон. — СПб.: Изд-во Санкт-Петербургского университета технологий управления и экономики, 2017. — 26 с.

 

Методические указания по выполнению контрольных работ для студентов заочной формы обучения представлены для студентов высших учебных заведений (бакалавров), обучающихся по направлению 380301 Экономика.

 

                                                                                 УДК                                                                                                    ББК

   

 

©Пономарев С.Е.

© СПбУТУиЭ, 2017

СОДЕРЖАНИЕ

1. Общие положения. 4

Тема 1. Постановка задач линейного программирования. 6

Тема 2. Симплексный метод решения канонической задачи линейного программирования. 8

Тема 3. Симплексный метод решения общей задачи линейного программирования. 9

Тема 4. Параметрическое программирование. 10

Тема 5. Транспортная задача. 11

Тема 6. Целочисленные задачи линейного программирования. 13

Тема 7. Сетевые методы в планировании и управлении. 16

Тема 8. Применение теории графов для решения задач оптимизации. 20

ЛИТЕРАТУРА.. 26

 

 

Общие положения

1.1. Цель изучения дисциплины

Цель изучения дисциплины «Методы оптимальных решений» - освоение математических методов решения задач, возникающих в экономике, финансах, менеджменте, маркетинге.

Задачи дисциплины - изучение методов исследования операций и их программных реализаций и обучение применению математических методов для обоснования управленческих решений.

1.2. Место дисциплины в учебном процессе, требования к знаниям и умениям студентов

Дисциплина «Методы оптимальных решений» относится к циклу обще профессиональных дисциплин, входящих в состав федерального компонента ГОС ВПО.

Предшествующими циклами дисциплины являются циклы общих гуманитарных и социально-экономических, общих математических и естественнонаучных дисциплин.

Место дисциплины в учебном процессе определяется дидактическими единицами, предшествующих в учебном плане базовых дисциплин: «Математика», «Теория вероятностей и математическая статистика», «Основы бизнеса».

Студент должен:

· знать математическое моделирование процессов оптимизации материальных и денежных потоков, вычислительные методы решения оптимизационных задач, применение MS Excel для поиска решений оптимизационных задач;

· уметь формулировать целевую функцию оптимизационных задач и записывать ограничения оптимизационных задач, представлять математическую модель оптимизационных процессов в виде электронной таблицы, программировать интерфейс пользователя оптимизационных задач;

· иметь навыки использования методов решения оптимизационных задач.

Содержание практических занятий

 

Тема 1. Постановка задач линейного программирования.

Оптимизация производственной программы. Приведение задач линейного программирования к каноническому виду. Графическая интерпретация задач линейного программирования.

Тема 2. Симплексный метод решения канонической задачи линейного программирования.

Алгоритм симплекс метода. Пересчет симплекс-таблицы. Условия сходимости симплекс-метода.

Тема 5. Транспортная задача

Решение закрытой транспортной задачи методом потенциалов. Приведение открытых транспортных задач к канонической задаче.

Тема 5. Транспортная задача

Изучаем тему на примере решения следующей задачи:

Задача 1.

Заданы поставщики и производители. Транспортная задача является открытой (возможности поставщиков меньше потребностей). Построить оптимальный план доставки, так, чтобы в пункт B₂  было  завезено не менее 25 единиц.

Ai	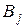15	36	40	42
50	4	14	2	5
20	5	11	3	10
30	3	8	11	1

РЕШЕНИЕ

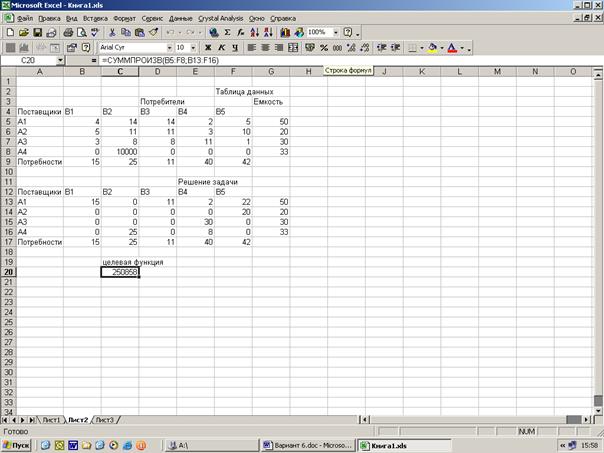
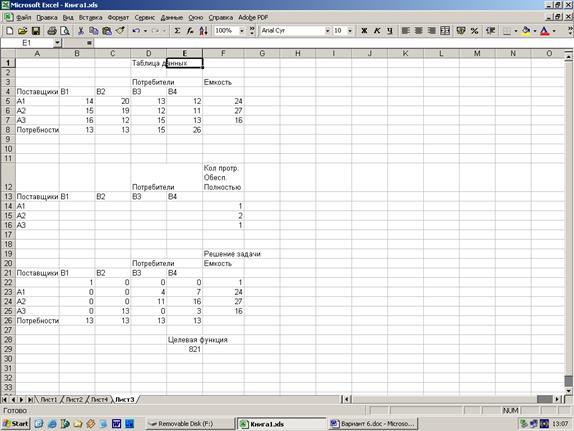
Закрываем транспортную задачу, вводя фиктивного поставщика с емкостью 33 единицы. Согласно методике решения транспортных задач, сокращаем потребность пункта B₂ до 25 единиц и задаем фиктивного потребителя с потребностью 11 единиц. Цену доставки от фиктивного поставщика в пункт B₂ задаем равной 10000. Цену доставки от фиктивного поставщика в остальные пункты задаем равной нулю. Вводим в таблицу данных исходные данные. В таблицу Решение задачи вводим неизвестные, ограничения и целевую функцию.

Ограничения:

=СУММ(B13:F13)

=СУММ(B14:F14)

=СУММ(B15:F15)

=СУММ(B16:F16)

=СУММ(B13:B16)

=СУММ(C13:B16)

=СУММ(D13:B16)

=СУММ(E13:B16)

=СУММ(F13:B16)

Целевая функция:

=СУММПРОИЗВ(B5:F8;B13:F16)

Запускаем Поиск решения, устанавливаем знаки ограничений и получаем ответ.

 

Задача 2

Заданы поставщики и потребители. Нужно построить оптимальный план поставки, при котором первый поставщик обеспечивает максимально возможное число потребителей.

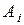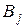
	11	10	17	29
27	14	20	13	12
27	15	19	12	11
16	16	12	15	13

РЕШЕНИЕ

Вначале определяем наибольшее количество потребителей, которых первый поставщик может обеспечить полностью. Для этого сортируем потребности p_i по возрастанию и находим такое число n, что сумма р₁+p₂+….+p_n меньше или равна емкости первого склада а сумма р₁+p₂+….+p_n +p_n+1 больше емкости первого склада. Найденное значение равно наибольшему количеству потребителей, обеспеченных полностью первым поставщиком. Для автоматизации данного процесса нужно составить программу на VBA

Вводим в таблицу данных исходные данные

В таблицу Решение задачи вводим неизвестные, ограничения и целевую функцию. В ячейках B22:E22 записываем значения переменных x1i, равных 1, если 1-ый поставщик обеспечивает полностью i-ого потребителя, и 0 в противном случае. В остальных ячейках таблицы решения задачи записываем вывоз груза. Сумма x1i равна числу потребителей, которых полностью обеспечил первый поставщик.

Вводим следующие ограничения:

=СУММ(B23:E23)+СУММПРОИЗВ(B22:E22;B8:E8)

=СУММ(B24:E24)

=СУММ(B25:E25)

=B8*B22+СУММ(B23:B25)

=C8*C22+СУММ(C23:C25)

=C8*C22+СУММ(C23:C25)

=C8*C22+СУММ(C23:C25)

Целевая функция:

=СУММПРОИЗВ(B5:E7;B23:E25)+СУММПРОИЗВ(B5:E5;B22:E22;B8:E8)

Запускаем Поиск решения, устанавливаем знаки ограничений и получаем ответ.

Тема 7. Сетевые методы в планировании и управлении

Задача о последовательной обработке.

Разработка системы нормативно-справочного обеспечения задач оптимизации производства

В связи с изменением технологии производства изменяются состав и нормы выработки технологических операций, состав, количество и производительность исполнителей при выполнении технологических операций. Состав выполняемых работ и количество исполнителей изменяется также при проведении планово-предупредительного и капитального ремонта. Поэтому актуальной задачей АСУ является обеспечение процессов оптимизации производства нормативно-справочной информацией.

Нет смысла копировать вручную данные из тарификационных справочников в таблицу поиска решений. Работа эта трудоемкая, и к моменту ее окончания данные становятся неактуальными.

Для решения задач нормативно-справочного обеспечения оптимизации производства нужна информационная система, заполняющая таблицу поиска решений данными, выбираемыми пользователем в тарификационном справочнике.

Процесс разработки данной системы изучаем на примере задачи об оптимальном распределении исполнителей по независимым работам. Рассмотрим ситуацию, когда на производственном участке выполняются n технологических операций и для их выполнения используются k исполнителей, имеющих разные производительности при выполнении конкретной технологической операции. Нужно распределить исполнителей по технологическим операциям так, чтобы к концу смены достичь максимального объема выпуска продукции в натуральном выражении. То есть, для конкретного исполнителя следует определить время выполнения той или иной технологической операции таким образом, чтобы к концу смены на производственном участке объем выпуска готовой продукции был наибольшим.

Сформулируем поставленную задачу как задачу оптимального программирования. Введем переменные x_ij- время выполнения i-ой операции j-ым исполнителем, (1 ≤ i ≤n, 1 ≤ j ≤k). Переменные x_ij удовлетворяют следующим ограничениям:

0 ≤ x_ij; 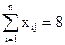, (1 ≤ j ≤k)        (1)

Обозначим p_ij производительность исполнителя j при выполнении технологической операции i, V_i- объем выполнения работы i. Объем выполнения работы i V_i равен

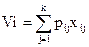, (1 ≤ i ≤n)

Между объемами выполнения технологических операций существуют линейные зависимости:

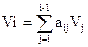, (2 ≤ i ≤n)                 (2)

Из (2) следует, что объемы V_i , (2 ≤ i ≤n), Выражаются через V₁. Таким образом, нужно найти наибольшее значение 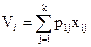, изменяя значения переменных x_ij, удовлетворяющих ограничениям (1), (2).

Задачу представляют в табличной форме. В расчетной таблице задают диапазон ячеек для записи значений переменных, формулу целевой функции и формулы ограничений. Для получения оптимальных значений переменных x_ij используется поиск решений, настроенный по формату таблицы оптимизационной задачи.

Для решения задачи используются справочник работ, тарификационный справочник и таблица связей между объемами выполнения технологических операций. Из справочника работ в автоматическом режиме в расчетную таблицу записываются наименования работ, выбираемых пользователем. Из тарификационного справочника в автоматическом режиме в расчетную таблицу записываются наименования исполнителей, выбираемых пользователем, из таблицы связей между объемами выполнения технологических операций в автоматическом режиме в расчетную таблицу записываются коэффициенты, выбираемые из строк, соответствующих работам, выполняемым на участке.

Для решения оптимизационной задачи нужно разработать информационные объекты, технологию работы пользователя и программное обеспечение.

Информационные объекты - это справочник работ, тарификационный справочник, таблица связей между объемами выполнения технологических операций и расчетная таблица. В справочнике работ заданы коды работ, наименования, единицы измерения и нормы выработки в единицу времени. В справочнике исполнителей заданы наименования рабочих профессий, разряды и производительность исполнителей при выполнении различных технологических операций. В таблице связей между объемами выполнения технологических операций заданы коэффициенты линейных зависимостей.

В справочнике работ пользователь отмечает работы, выполняемые за смену, в тарификационном справочнике пользователь указывает количество конкретных исполнителей, работающих по графику. Эти данные записываются в расчетную таблицу.

Программа заполнения расчетной таблицы состоит из трех процедур:

1. Процедура заполнения списка выбранных работ

2. Процедура заполнения списка выбранных профессий

3. Процедура вычисления производительности исполнителей выбранных работ

Первые две процедуры – стандартные программы работы со справочной информацией. Третья программа вычисляет с помощью стандартной операции поиска образца в документе номера строк, соответствующих выбранным пользователем наименованиям работ, номера граф, соответствующих выбранным пользователем наименованиям исполнителей, и записывает их в массивы. По найденным массивам определяются ячейки расчетной таблицы, в которые записываются данные, необходимые для решения оптимизационной задачи. Ниже приводятся тексты процедур.

 

Процедура заполнения списка выбранных работ

n=3: k=5

while worksheets(«Справочник»).cells(n,2)<>””

worksheets(«Оптимизация»).cells(k,1)= worksheets(«Справочник»).cells(n,1)

k=k+1: n=n+1: wend

 

Процедура заполнения списка выбранных профессий

 

n=3: k=5

while worksheets(«Справочник»).cells(n,5)<>””

worksheets(«Оптимизация»).cells(3,k)= worksheets(«Справочник»).cells(n,4)

worksheets(«Оптимизация»).cells(4,k)= worksheets(«Справочник»).cells(n,5)

k=k+1: n=n+1: wend

 

Процедура вычисления производительности исполнителей выбранных работ

 

n=3:dim a(100) as integer: dim b(100) as integer

while worksheets(«Оптимизация»).cells(n,1)<>””

c= worksheets(«Оптимизация»).cells(n,1)

k=2: while worksheets(«Справочник»).cells(k,1)<>c and Worksheets(«Справочник»).cells(k,1)<>””

k=k+1: wend: a(n)=k

n=n+1: wend

n=5

while worksheets(«Оптимизация»).cells(3,n)<>””

c= worksheets(«Оптимизация»).cells(3,n)

k=2: while worksheets(«Справочник»).cells(k,4)<>c and Worksheets(«Справочник»).cells(k,4)<>””

k=k+1: wend: b(n)=k

n=n+1: wend

n=3

while worksheets(«Оптимизация»).cells(n,1)<>””

r=a(n)

k=5: while worksheets(«Оптимизация»).cells(3,k)<>””

e=b(k)

worksheets(«Оптимизация»).cells(n,k)= worksheets(«Оптимизация»).cells(4,k)* Worksheets(«Справочник»).cells(r,e)

n=n+1: wend

ЛИТЕРАТУРА

а) основная литература:

1. Черноруцкий И. Методы оптимизации. Компьютерные технологии [Электронный ресурс].- СПб. : БХВ-Петербург, 2011.-384 с.- Электронное издание. - Гриф УМО.- ISBN 978-5-9775-0784-4

2. Аттетков, А.В. Введение в методы оптимизации [Электронный ресурс].- Электронное издание.- М.: Финансы и статистика, 2011.- 272 с

б) дополнительная литература:

3. Т.В.Ростовцева, В.И. Фомин, С.Е.Пономарев. Применение алгоритмов теории графов для оптимизации в строительстве и производстве. Санкт-Петербург, 2012, Ó СПбГИЭУ, 2012.

4. С.Е.Пономарев. Теория графов и параллельные вычисления в нефтегазовом комплексе, 2014, Ó LAMBERT Akademic publishing.

МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ

Методические указания

 по выполнению контрольных работ для студентов заочной формы обучения, обучающихся  по направлению 380301 Экономика

 

 

Санкт-Петербург

2017

УДК

 

Рассмотрено и рекомендовано к изданию Методическим советом

Института экономики, менеджмента и информационных технологий

(протокол № _____ от «___» __________ 2017 г.)

 

Составители:

кандидат технических наук С.Е. Пономарев

Рецензент

доцент кафедры Информационных технологий и математики СПбУТУиЭ

кандидат технических наук Е.Е. Майоров

0-64  Методы оптимальных решений: методические указания по выполнению контрольных работ для студентов заочной формы обучения / сост. В.В. Курлов, ун-т технол. упр. и экон. — СПб.: Изд-во Санкт-Петербургского университета технологий управления и экономики, 2017. — 26 с.

 

Методические указания по выполнению контрольных работ для студентов заочной формы обучения представлены для студентов высших учебных заведений (бакалавров), обучающихся по направлению 380301 Экономика.

 

                                                                                 УДК                                                                                                    ББК

   

 

©Пономарев С.Е.

© СПбУТУиЭ, 2017

СОДЕРЖАНИЕ

1. Общие положения. 4

Тема 1. Постановка задач линейного программирования. 6

Тема 2. Симплексный метод решения канонической задачи линейного программирования. 8

Тема 3. Симплексный метод решения общей задачи линейного программирования. 9

Тема 4. Параметрическое программирование. 10

Тема 5. Транспортная задача. 11

Тема 6. Целочисленные задачи линейного программирования. 13

Тема 7. Сетевые методы в планировании и управлении. 16

Тема 8. Применение теории графов для решения задач оптимизации. 20

ЛИТЕРАТУРА.. 26

 

 

Общие положения

1.1. Цель изучения дисциплины

Цель изучения дисциплины «Методы оптимальных решений» - освоение математических методов решения задач, возникающих в экономике, финансах, менеджменте, маркетинге.

Задачи дисциплины - изучение методов исследования операций и их программных реализаций и обучение применению математических методов для обоснования управленческих решений.

1.2. Место дисциплины в учебном процессе, требования к знаниям и умениям студентов

Дисциплина «Методы оптимальных решений» относится к циклу обще профессиональных дисциплин, входящих в состав федерального компонента ГОС ВПО.

Предшествующими циклами дисциплины являются циклы общих гуманитарных и социально-экономических, общих математических и естественнонаучных дисциплин.

Место дисциплины в учебном процессе определяется дидактическими единицами, предшествующих в учебном плане базовых дисциплин: «Математика», «Теория вероятностей и математическая статистика», «Основы бизнеса».

Студент должен:

· знать математическое моделирование процессов оптимизации материальных и денежных потоков, вычислительные методы решения оптимизационных задач, применение MS Excel для поиска решений оптимизационных задач;

· уметь формулировать целевую функцию оптимизационных задач и записывать ограничения оптимизационных задач, представлять математическую модель оптимизационных процессов в виде электронной таблицы, программировать интерфейс пользователя оптимизационных задач;

· иметь навыки использования методов решения оптимизационных задач.

Содержание практических занятий

 

Тема 1. Постановка задач линейного программирования.

Оптимизация производственной программы. Приведение задач линейного программирования к каноническому виду. Графическая интерпретация задач линейного программирования.