Nu = α*l/λ,
где l – характерный геометрический размер твёрдой стенки, определяемый по своей зависимости в каждом рассматриваемом процессе теплоотдачи.
В задачах о теплоотдаче число Нуссельта является искомой величиной, т.к. в него входит необходимый для расчёта теплообменного аппарата коэффициент теплоотдачи.
Безразмерный комплекс (Re)
Re = w*l/ν = w*l*ρ/µ
Называют числом Рейнольдса.
В это соотношение входят:
w – скорость текучей среды;
ν и µ - коэффициенты кинематической и динамической вязкости жидкости (газа) соответственно.
Число Рейнольдса представляет собой отношение сил инерции, действующих в жидкости (газе), к силам вязкости. Это число достаточно полно характеризует режим течения жидкости.
Безразмерную величину
Pr = µ*cp/λ,
в которой сp – удельная массовая теплоёмкость текучей среды, называют числом Прандтля. Это число состоит только лишь из физических параметров жидкости (газа) и потому и само число Прандтля представляет собой физическую характеристику вещества.
5.3.2.2. Пример использования теории подобия.
Следует иметь в виду, что весьма сложная математическая модель описания конвективной теплоотдачи в общем случае не позволяет выполнить точное моделирование всех процессов. Поэтому в курсовой работе используются упрощенные приёмы теории подобия.
Пусть необходимо вычислить коэффициент теплоотдачи при течении воды в трубках водяного подогревателя. Массовый расход воды равен G = 16670кг/час, её плотность – ρ = 1000кг/м3 , температура воды t = 110°С. Площадь сечения всех трубок теплообменника равна f = 0,00507м2, а внутренний диаметр одной трубки – d = 13,2мм.
Определяем число Рейнольдса при течении воды в трубках (для идентификации режима течения жидкости и установления динамического условия однозначности).
Re = w*d/ν,
где w = G/(ρ*f) = 16670/(3600*1000*0,00507) = 0,913м/с – скорость течения воды в трубках.
По таблице №1 приложения методического пособия определяем кинематический коэффициент вязкости воды при температуре t = 110°С – ν = 0,27210-6м2/c и число Прандтля воды – Pr = 1,6.
Тогда, число Рейнольдса
Re = 0,913*0.0132/0,27210-6м2 = 44300
При таком числе Рейнольдса наблюдается развитое турбулентное течение воды и потому влиянием естественной конвекции на теплоотдачу можно пренебречь. Такой физической модели течения воды соответствует критериальная зависимость для определения теплоотдачи [4]
Nu = 0,021*Re0,8*Pr0,43
В этой зависимости использовано среднее по длине трубы значение числа Нуссельта и, следовательно, в результате будет получено среднеинтегральное значение коэффициента теплоотдачи. Кроме того, эта зависимость не учитывает переменность свойств капельной жидкости в зависимости от температуры. Это следует иметь в виду, т.к. эти факторы различают реальную физическую модель и условия эксперимента.
Итак, Nu = 0,021*443000.8*1,60.43 = 134
и коэффициент теплоотдачи
α = Nu*λ/d = 134*0,685/0,0132 = 6950Вт/(м2*°С)
В этой зависимости λ = 0,685Вт/(м*°С) – коэффициент теплопроводности воды (таблица №1, Приложение).
Итак, приведен пример, который наглядно показывает, насколько существенно теория подобия упрощает расчёты конвективной теплоотдачи.
5.4. Основные положения теплового и компоновочного расчётов теплообменных аппаратов.
5.4.1. Основные понятия и определения, формулировка задачи.
В предлагаемых курсовых работах расчёту подлежат теплообменные аппараты (или теплообменники), называемые рекуператорами. Рекуператоры – это теплообменники, в которых две текучие среды, имеющие разные температуры, обмениваются теплотой через разделяющую их стенку. Эти среды - теплоносители - могут быть как жидкими, так и газообразными веществами. В процессе переноса теплоты они могут сохранять, но могут и изменять своё фазовое состояние – в теплообменном аппарате может происходить процесс кипения жидкости или процесс конденсации газа.
Процессы в теплообменных аппаратах могут происходить как стационарные, так и нестационарные – неустановившиеся. В предлагаемых курсовых работах рассматриваются стационарные рекуператоры.
В рекуперативных теплообменниках процесс распространения теплоты в пространстве осуществляется теплопередачей. Каждый из двух текучих теплоносителей при движении в теплообменнике обменивается теплотой с его стенкой в результате конвективной теплоотдачи, а через стенку теплота распространяется теплопроводностью. Таким образом, одно из уравнений, описывающих процесс распространения теплоты в рекуператоре – это уравнение теплопередачи.
Понятно также, что при распространении теплоты в рекуператоре один из теплоносителей отдаёт тепло, а второй именно это количество тепла воспринимает. Отсюда следует, что вторым уравнением для расчёта теплообменного аппарата должно служить уравнение теплового баланса.
Таким образом, тепловой расчёт рекуператора сводится к совместному решению уравнений теплового баланса и теплопередачи.
5.4.2. Уравнение теплового баланса
В теплообменных аппаратах, как правило, изменение давления по ходу движения теплоносителя невелико. Так проектируют теплообменники из-за стремления уменьшить расходы энергии на их эксплуатацию. В то же время, из курса “Термодинамики” известно, что в изобарном процессе (давление теплоносителя неизменно) подведенная (отведенная) теплота изменяет энтальпию теплоносителя
dQ = G*di
В этом уравнении
Q – тепловой поток (Дж/c);
G – массовый расход теплоносителя (кг/с);
i – удельная энтальпия теплоносителя (Дж/кг).
Интегрируя это уравнение, получим для всего процесса теплопередачи
Q = G*(i'' - i').
Здесь и далее обозначения параметров со штрихом относятся к параметрам теплоносителя перед теплообменником (на входе), а с двумя штрихами – после теплообменника (на выходе).
Так как в теплообменном аппарате теплота от горячего теплоносителя воспринимается холодным теплоносителем, то уравнение теплового баланса запишется так:
Q = G1*(i'1 – i''1) = G2*(i''2 - i'2).
Здесь и далее подстрочный индекс 1 относится к параметрам горячего теплоносителя, а индекс 2 – к параметрам холодного теплоносителя.
Полагая, что удельная массовая теплоёмкость теплоносителя величина неизменная и используя известное из “Термодинамики” соотношение
i = cp*t,
получим
C1/C2 = (t''2 - t'2)/(t'1 - t''1)
В этом уравнении С1 = G1*сp1 и С2 = G2*сp2 – полная теплоёмкость массового расхода теплоносителя или его водяной эквивалент.
Последнее уравнение показывает, что отношение изменений температур однофазных теплоносителей в теплообменнике обратно пропорционально отношению водяных эквивалентов теплоносителей. Для случая однофазных теплоносителей уравнение теплового баланса используется в приведенном виде.
Для случая, когда один из теплоносителей претерпевает в теплообменнике фазовый переход от степени сухости 1 до степени сухости пара 0 (при полной конденсации насыщенного влажного пара), уравнение теплового баланса принимает следующий вид:
Q = G1*r = G2*cp2*(t''2 - t'2),
где r – скрытая теплота парообразования теплоносителя.
5.4.3. Уравнение теплопередачи
Из самого определения процесса теплопередачи ясно, что уравнение теплопередачи должно быть получено совместным решением двух уравнений конвективной теплоотдачи и уравнения распространения тепла через плоскую стенку. В некоторых курсовых работах следует использовать уравнение теплопроводности многослойной стенки (для учета загрязнений и других отложений на поверхностях стенки).
Решение этой системы уравнений в дифференциальной форме имеет вид [4]
dQ = k*Δt*dF
В этом уравнении:
Q – тепловой поток (Вт);
k –коэффициент теплопередачи (Вт/(м2*К));
Δt – локальный температурный напор на элементарном участке поверхности теплообмена dF.
Коэффициент теплопередачи определяется по зависимости
k = 1/(1/α1 + R + 1/α2),
где α1 и α2 – коэффициенты теплоотдачи горячего и холодного теплоносителей,
R – термическое сопротивление многослойной (однослойной) стенки.
Понятно, что для определения общего теплового потока (теплопроизводительности теплообменника) необходимо проинтегрировать это уравнение. Коэффициент теплопередачи изменяется в теплообменных аппаратах, как правило, незначительно и, поэтому, при интегрировании уравнения теплопередачи его принимают постоянным. А вот локальный температурный напор изменяется вдоль теплопередающей поверхности значительно. Поэтому, уравнение теплопередачи в расчётах используется в несколько изменённом виде, путём применения среднеинтегрального температурного напора. Понятно, для того, чтобы проинтегрировать температурный напор по площади поверхности теплообмена, необходимо предварительно определить закон изменения напора вдоль по поверхности. Изменение температурного напора вдоль по поверхности теплообмена рекуператора зависит от схемы движения теплоносителей и от соотношения водяных эквивалентов теплоносителей. Схемы движения теплоносителей прямоточного и противоточного теплообменников, а также схема для расчёта среднеинтегрального по поверхности теплообмена температурного напора приведены на рисунках.
|
|
|



|
|
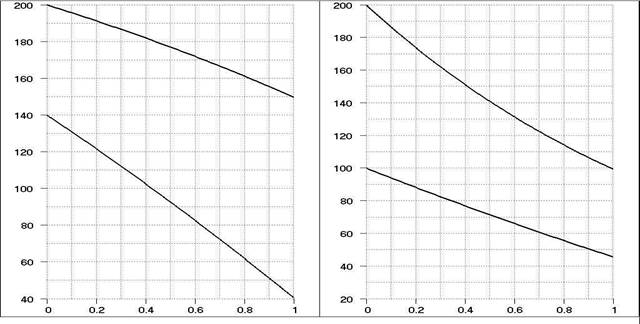
Изменение температуры теплоносителей в противоточном рекуператоре
|
|
|
|
|



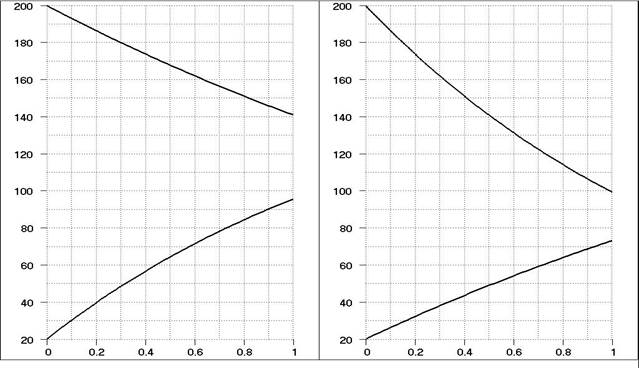
Изменение температуры теплоносителей в прямоточном рекуператоре
| |

| |

| |
|
|

|
|
|
|





|
|
|
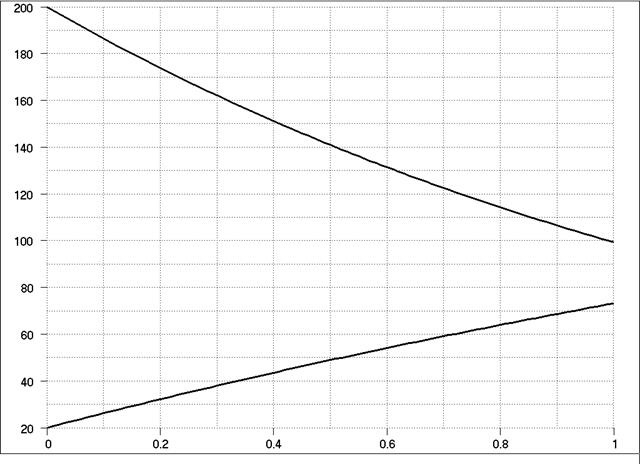
Схема расчёта среднеинтегрального (среднелогарифмического) температурного напора рекуператора
В [4] получена зависимость для определения среднеинтегрального (обычно его называют среднелогарифмическим) температурного напора;
Δtс = (Δtб – Δtм)/ln(Δtб/ Δtм),
где Δtб и Δtм – больший и меньший температурный напоры из двух напоров - на входе и выходе теплоносителей из теплообменника.
С учётом сделанных замечаний уравнение полной теплопередачи (теплопроизводительности) теплообменника принимает вид;
Q = k*Δtс*F
Заключение
Приведенные выше зависимости, понятия и определения достаточны для проведения как проектных тепловых и компоновочных расчётов рекуператоров, так и для проверочных расчётов, в которых по типу теплопередающей поверхности, величине её площади и по параметрам теплоносителей на входе в теплообменник определяют температуры теплоносителей на выходе.
Однако, практические расчёты зачастую изобилуют необходимостью использования разнообразных приёмов для рационального проведения расчётов. Например, в случаях проведения расчётов методом последовательных приближений. Поэтому в приложении к методическому пособию приведены примеры тепловых и компоновочных расчётов четырёх разных типов рекуператоров. Эти рекуператоры отличаются своими конструкциями и процессами теплоотдачи – в одних теплоносители изменяют своё агрегатное состояние, а в других – не изменяют. Такой подход обеспечивает более широкое знакомство студентов и с конструкцией теплообменных аппаратов и с тепловыми процессами, протекающими в рекуператорах.
Приложения
Примеры тепловых и компоновочных расчётов теплообменных аппаратов
Курсовая работа №1
Произвести тепловой расчет пароводяного подогревателя горизонтального типа.
Производительность подогревателя Q = 1,1636МВт = 106ккал/час.
Температура нагреваемой воды на входе в подогреватель t21 = 700C, а на выходе –t211 = 950С.
Абсолютное давление сухого насыщенного пара Р = 4ат; температура конденсата на выходе равна температуре насыщения (tн); число ходов теплообменника по нагреваемой воде z = 2; поверхность нагрева – латунные трубы (коэффициент теплопроводности λ ≈ 105Вт/мК ≈ 90ккал/м*час*К) диаметром dвн./dн = 14/16мм. Загрязнение поверхности учесть дополнительным тепловым сопротивлением δ3/λ3 = 0,00015м2*час*К/ккал ≈ 0,00013м2К/Вт
На основе расчетов выбрать аппарат, выпускаемый серийно.
Дата: 2018-12-28, просмотров: 557.