Путем последовательного соединения ФВЧ и ФНЧ получают полосовой фильтр. Его выходное напряжение равно 0 на высоких и низких частотах.

Выходное напряжение полосового RC-фильтра

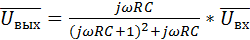                  .                          (9.42)

  Рис.9.14. Пассивный полосовой RC-фильтр (а) и его АЧХ (б)

Коэффициент усиления

                        .             (9.43)

Отсюда модуль коэффициента усиления и фазовый сдвиг

            ,    .          (9.44)

Выходное напряжение максимально при ω RC = 1, следовательно, резонансная частота

                                ;                                           (9.45)

 - нормированная частота.

Фазовый сдвиг на резонансной частоте равен 0. Коэффициент усиления K_р = 1/3.

Если в схеме рис.9.14 заменить сопротивления на индуктивность, то получим схему пассивного полосового LC-фильтра (рис.9.15).

Рис.9.15. Схема пассивного полосового LC-фильтра (а) и его АЧХ (б)

При совпадении частот, на которых наблюдается резонанс напряжений в последовательном контуре L₁C₁ и резонанс токов в параллельном колебательном контуре L₂C₂, сопротивление продольного плеча L₁C₁ оказывается минимальным, а поперечного L₂C₂ – максимальным. Коэффициент передачи ПФ при этом имеет наибольшее значение. При отклонении частоты входных колебаний от резонансной частоты ƒ₀ коэффициент передачи ПФ уменьшается (рис. 9.15,б).

Заграждающие полосовые фильтры

АЧХ заграждающего фильтра может быть получена из частотной характеристики ФНЧ путем замены переменной Р выражением ΔΩ/(P+1/P). Здесь ΔΩ = 1/Q нормированная полоса частот. Q = f_р/(f _max – f _min ) = f_р/Δf, где Δf – полоса частот, на краях которой коэффициент передачи падает на 3 дБ (Q – добротность подавления сигнала).

Как и в случае полосовых фильтров при преобразовании порядок фильтра удваивается. Так при преобразовании передаточной функции ФНЧ первого порядка получим заграждающий фильтр второго порядка с передаточной функцией

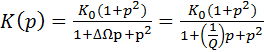                  .                       (9.46)

Отсюда получим выражения для АЧХ и ФЧХ фильтра

   .         (9.47)

Пассивный заграждающий RLC -фильтр

Пример пассивного заграждающего фильтра приведен на рис. 9.16. Передаточная функция такого фильтра имеет вид

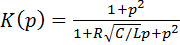                       .                                  (9.48)

Рис.9.16. Схема заграждающего RLC-фильтра

Резонансная частота и добротность подавления находятся как

                            .                         (9.49)

Примерами пассивных заграждающих фильтров являются также мост Вина – Робинсона (рис. 9.17) и двойной Т-образный мост (рис. 9.18).

Мост Вина-Робинсона

Рис.9.17. Схема фильтра Мост Вина-Робинсона

Омический делитель напряжения обеспе­чивает частотно-независимое напряжение, равное 1/3U _вх.

При этом на резонансной частоте выходное напряжение равно 0. В отличие от полосового фильтра АЧХ коэффициента усиления на резонансной частоте имеет минимум. Схема применима для подавления сигналов в определенной частотной области.

Коэффициент передачи

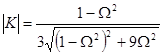                        ;                         (9.50)

Фазовый сдвиг

                    .                               (9.51)

Двойной Т-образный фильтр

Двойной Т-образный фильтр обладает частотной характеристикой, идентичной характеристике моста Вина-Робинсона.

     Рис.9.18. Двойной Т-образный фильтр (а) и его АЧХ (б)

В отличие от моста Вина-Робинсона выходное напряжение снимается относительно общей точки.

Для высоких и низких частот U _вых = U _вх.

Сигналы высоких частот будут полностью передаваться через два конденсатора С, а низких через резистор R.

Коэффициент передачи и фазовый сдвиг:

                   ,  .               (9.52)

Добротность данных фильтров мала. Она может быть повышена, если включить их в цепь обратной связи усилителя.