Фильтры нижних частот
Фильтр нижних частот является схемой, которая без изменений передает сигналы нижних частот, а на высоких частотах обеспечивает затухание сигналов и запаздывание их по фазе относительно входных сигналов.
Активные фильтры нижних частот первого порядка
Простой фильтр, изображенный на рис.9.1, обладает недостатком: свойства фильтра зависят от нагрузки. Для устранения этого недостатка фильтр необходимо дополнить преобразователем полного
Рис.9.3. Активный ФНЧ первого порядка с
преобразователем полного сопротивления
сопротивления. Схема фильтра с преобразователем полного сопротивления показана на рис.9.3. Коэффициент передачи постоянного сигнала может быть задан выбором значений резисторов R2 и R3:
. (9.19)
Для упрощения схемы ФНЧ можно использовать RC-цепь для обратной связи операционного усилителя. Подобный фильтр показан на рис.9.4.
Рис.9.4. Активный ФНЧ первого порядка
Передаточная функция фильтра (рис.9.4) имеет вид
. (9.20)
Для расчета фильтра необходимо задать частоту среза fср (ωср), коэффициент передачи постоянного сигнала К0 (для схемы на рис.9.4 он должен быть задан со знаком минус) и емкость конденсатора С1. Приравняв коэффициенты полученной передаточной функции коэффициентам выражения 9.18 для фильтра первого порядка, получим
. (9.21)
Пассивный фильтр нижних частот второго порядка
На основании выражения (9.18) запишем в общем виде передаточную функцию ФНЧ второго порядка
. (9.22)
Такая передаточная функция не может быть реализована с помощью пассивных RC-цепей. Подобный фильтр может быть реализован с применением индуктивностей. На рис.9.5 показана схема пассивного ФНЧ второго порядка.
Рис.9.5. Пассивный ФНЧ второго порядка
Передаточная функция фильтра имеет вид
. (9.23)
Рассчитать фильтр можно, воспользовавшись формулами
. (9.24)
Например, для ФНЧ второго порядка типа Баттерворта с коэффициентами а1 = 1,414 и b 1 = 1,000, задав частоту среза f ср= 10 Гц и емкость С = 10мкФ, из (9.24) получим R = 2,25 кОм и L = 25,3 Гн.
Подобные фильтры неудобны для реализации из-за слишком большой индуктивности. Заданную передаточную функцию можно реализовать с помощью операционного усилителя с соответствующими RC – цепями, что позволяет исключить индуктивности.
Фильтры верхних частот
Используя логарифмическое представление, можно перейти от нижних частот к верхним, зеркально отобразив АЧХ коэффициента передачи относительно частоты среза, т.е. заменив Ω на 1/Ω или P на 1/P. При этом частота среза остается неизменной, а К0 переходит К∞. При этом получим
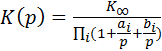. (9.29)
Полосовые фильтры
Путем замены переменной Р в передаточной функции ФНЧ на переменную (1/ΔΩ)(P+1/P) можно получить АЧХ полосового фильтра. В результате этого преобразования АЧХ фильтра нижних частот в диапазоне 0 ≤ Ω ≤ 1 переходит в правую часть полосы пропускания полосового фильтра (1 ≤ Ω ≤ Ωmax). Левая часть полосы пропускания является зеркальным отображением в логарифмическом масштабе правой части относительно средней частоты полосового фильтра Ω = 1 (рис. 9.13). При этом Ω min = 1/ Ω max. Вычисление нормированных частот среза полосового фильтра, на которых его коэффициент передачи уменьшается на 3 дБ, может быть осуществлено из
(9.41)
формулы, которая получается при
.
Рис.9.13. АЧХ полосового фильтра
Мост Вина-Робинсона
Рис.9.17. Схема фильтра Мост Вина-Робинсона
Омический делитель напряжения обеспечивает частотно-независимое напряжение, равное 1/3U вх.
При этом на резонансной частоте выходное напряжение равно 0. В отличие от полосового фильтра АЧХ коэффициента усиления на резонансной частоте имеет минимум. Схема применима для подавления сигналов в определенной частотной области.
Коэффициент передачи
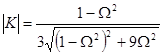; (9.50)
Фазовый сдвиг
. (9.51)
Двойной Т-образный фильтр
Двойной Т-образный фильтр обладает частотной характеристикой, идентичной характеристике моста Вина-Робинсона.
Рис.9.18. Двойной Т-образный фильтр (а) и его АЧХ (б)
В отличие от моста Вина-Робинсона выходное напряжение снимается относительно общей точки.
Для высоких и низких частот U вых = U вх.
Сигналы высоких частот будут полностью передаваться через два конденсатора С, а низких через резистор R.
Коэффициент передачи и фазовый сдвиг:
, 
. (9.52)
Добротность данных фильтров мала. Она может быть повышена, если включить их в цепь обратной связи усилителя.
Фильтры нижних частот
Фильтр нижних частот является схемой, которая без изменений передает сигналы нижних частот, а на высоких частотах обеспечивает затухание сигналов и запаздывание их по фазе относительно входных сигналов.
Пассивные фильтры нижних частот первого порядка
Рис.9.1. Пассивный ФНЧ первого порядка
На рис.9.1. изображена схема простого RС-фильтра нижних частот первого порядка. Коэффициент передачи в комплексном виде может быть выражен формулой:
. (9.7)
Отсюда получим формулы для АЧХ и ФЧХ:
. (9.8)
Положив 
, получим выражение для частоты среза ωср :
. (9.9)
| К | = 1 = 0 дБ на нижних частотах f << f ср.
На высоких частотах f >> f ср согласно формуле (9.8) |К| ≈ 1/ (ωRC), т.е. коэффициент передачи обратно пропорционален частоте. При увеличении частоты в 10 раз коэффициент усиления уменьшается в 10 раз, т. е. он уменьшается на 20 дБ на декаду или на 6 дБ на октаву. 
при f = f ср.
Пример расчета пассивного ФНЧ первого порядка.
Произведем расчет коэффициента передачи по формуле 9.8. Для этого примем, что R = 1 кОм и С = 1 мкФ. Будем принимать частоту от 0,001 Гц до 100 кГц с шагом 10. Получаем следующие расчеты коэффициента передачи фильтра:
Рис.9.2. Зависимость коэффициента передачи фильтра ФНЧ от частоты
Построим график зависимости коэффициента передачи от частоты (рис.9.2).
Таким образом, видим, что ФНЧ обеспечивает нормальное прохождение низких частот и задерживает верхние частоты.
Для более быстрого уменьшения коэффициента передачи можно включить n фильтров нижних частот последовательно. При последовательном соединении нескольких фильтров нижних частот частота среза приближенно определяется как
. (9.10)
Для случая n фильтров с равными частотами среза
. (9.11)
При частоте входного сигнала f вх >> f ср для схемы (рис.9.1) получим
. (9.12)
Из (9.12) видно, что ФНЧ может выступать как интегрирующее звено.
Для переменного напряжения, содержащего постоянную составляющую, выходное напряжение можно представить в виде
, (9.13)
где 
- среднее значение.
Фильтр нижних частот может выступать в качестве детектора средних значений.
Для реализации общего подхода к описанию фильтров необходимо нормировать комплексную переменную р:
. (9.14)
Для фильтра рис.9.1 получим Р = рRC и
. (9.15)
Используя передаточную функцию для оценки амплитуды выходного сигнала от частоты, получим
. (9.16)
Передаточная функция ФНЧ в общем виде может быть записана в виде 
, (9.17)
где с1, с2 ,…, сn– положительные действительные коэффициенты.
Порядок фильтра определяется максимальной степенью переменной Р. Для реализации фильтра необходимо разложить полином знаменателя на множители. Если среди корней полинома есть комплексные, в этом случае следует записать полином в виде произведения сомножителей второго порядка
, (9.18)
где а i и bi– положительные действительные коэффициенты. Для нечетных порядков полинома коэффициент b 1 равен нулю.
Дата: 2018-12-28, просмотров: 1270.
