Примером активного ФНЧ второго порядка является фильтр со сложной отрицательной обратной связью, схема которого показана на рис. 9.6. Передаточная функция данного фильтра имеет вид
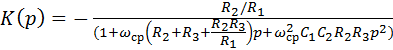 . (9.25)
. (9.25)

Рис.9.6. Активный ФНЧ второго порядка
Для расчета фильтра можно записать 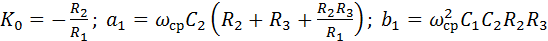 . (9.26) При расчете схемы лучше задавать значения емкостей конденсаторов и вычислять необходимые значения сопротивлений:
. (9.26) При расчете схемы лучше задавать значения емкостей конденсаторов и вычислять необходимые значения сопротивлений:
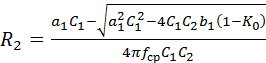 ;
;
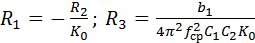 . (9.27)
. (9.27)
Для того, чтобы значение сопротивления R2 было действительным, должно выполняться условие
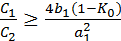 . (9.28)
. (9.28)
Фильтры с отрицательной ОС имеют с высокую добротность.
Активный ФНЧ второго порядка может быть построен на основе ОУ с омической отрицательной обратной связью и на основе ОУ с положительной обратной связью. Примеры подобных фильтров показаны на рис.9.7 и рис.9.8.
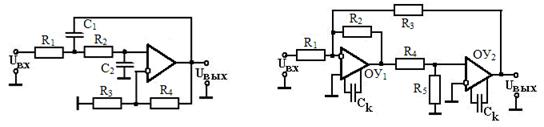
| Рис.9.7 Активный ФНЧ второго порядка с омической отрицатель- ной ОС | Рис.9.8 Активный ФНЧ второго порядка с положительной ОС |
Фильтры верхних частот
Используя логарифмическое представление, можно перейти от нижних частот к верхним, зеркально отобразив АЧХ коэффициента передачи относительно частоты среза, т.е. заменив Ω на 1/Ω или P на 1/P. При этом частота среза остается неизменной, а К0 переходит К∞. При этом получим
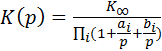 . (9.29)
. (9.29)
Пассивные ФВЧ первого порядка
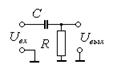
Рис.9.9. Пассивный ФВЧ первого порядка
Схема простого пассивного ФВЧ первого порядка приведена на рис. 9.9. ФВЧ передает без изменения сигналы высоких частот, а на низких частотах обеспечивает затухание сигналов и опережение их по фазе относительно входных сигналов. Коэффициент передачи в комплексной форме может быть записан в виде
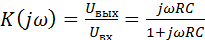 . (9.30)
. (9.30)
Отсюда находим выражения для АЧХ, ФЧХ и частоты среза
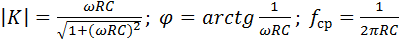 . (9.31)
. (9.31)
При f = fср, как и для фильтра нижних частот,
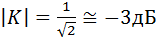 .
.
Если приложено входное напряжение с частотой f<<fср, то 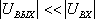 , и из уравнения
, и из уравнения
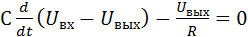 (9.32)
(9.32)
получим
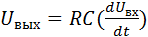 . (9.33)
. (9.33)
Таким образом, входные напряжения низкой частоты дифференцируются, т.е. ФВЧ может выступать как дифференцирующий преобразователь.
При последовательном соединении нескольких ФВЧ результирующая частота среза
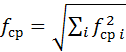 . (9.34)
. (9.34)
Если все фильтры имеют равные частоты среза, то
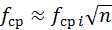 . (9.35)
. (9.35)
Пример расчета пассивного ФВЧ первого порядка.
Произведем расчет коэффициента передачи по формуле 9.31. Для этого примем, что R = 1 кОм и С = 10 мкФ. Будем принимать частоту от 0,001 Гц до 100 кГц с шагом 10. Получаем следующие расчеты коэффициента передачи фильтра:
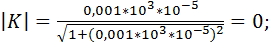
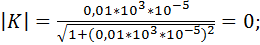
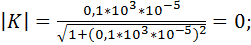
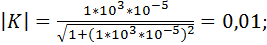
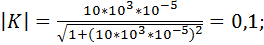
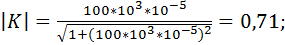
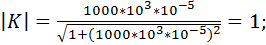
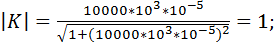
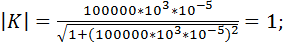
Построим график зависимости коэффициента передачи от частоты (рис.9.10):
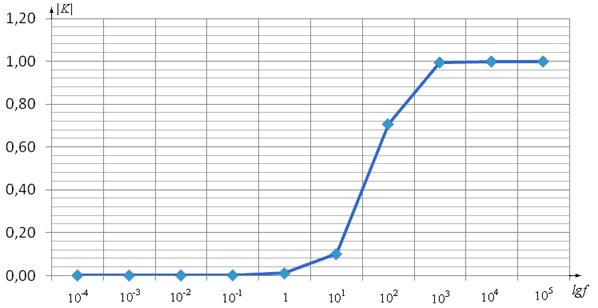
Рис.9.10. Зависимость коэффициента передачи фильтра от частоты
Таким образом, видим, что ФВЧ обеспечивает нормальное прохождение высоких частот и задерживает низкие частоты.
Дата: 2018-12-28, просмотров: 1126.