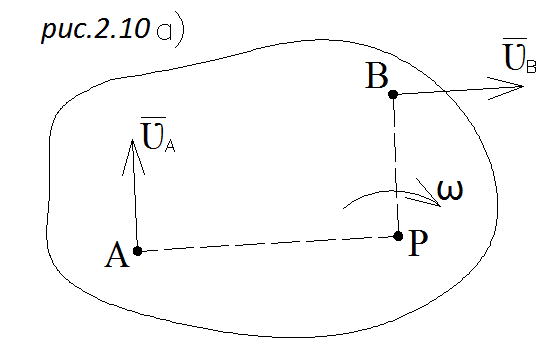
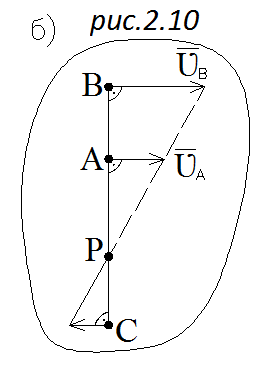
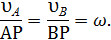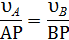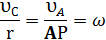Пусть известны направления скоростей двух точек плоской фигуры 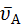 и
и 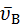 .
.
|
| Проведем из точек А и В перпендикуляры к скоростям. Точка их пересечения Р является м.ц.с (рис. 2.10). Скорости точек А и В пропорциональны расстояниям до м.ц.с.
| |||
|
Пусть точка А и В лежат на одном перпендикуляре (рис. 2.10, б). Расстояние АР до м.ц.с. можно найти из свойства пропорциональности скоростей расстояниям до м.ц.с.
|
| |||
|
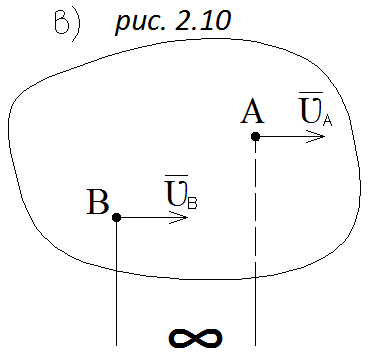
Пусть скорость точек А и В параллельны (рис. 2.10, в) в этом случае м.ц.с. находится в бесконечности, скорости всех точек геометрически равна, угловая скорость
| |||
|
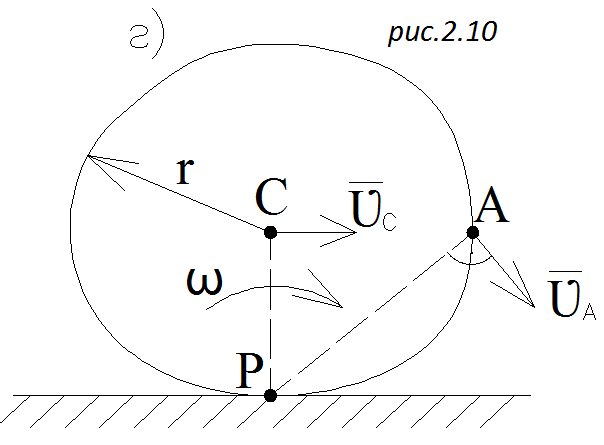
При качении колеса без проскальзывания м.ц.с. находится в точке соприкосновения колеса и дороги (рис. 2.10, г)
| 
| |||
Во вращательном движении центр вращения неподвижен, в плоском движении м.ц.с. меняет свое положение. Возьмем лист (подвижную плоскость) и в каждый момент времени будем прокалывать его и отмечать м.ц.с., на неподвижной и подвижной плоскости.
Геометрическое место м.ц.с. на неподвижной плоскости, называется неподвижной центроидой, на подвижной плоскости – подвижной центроидой.
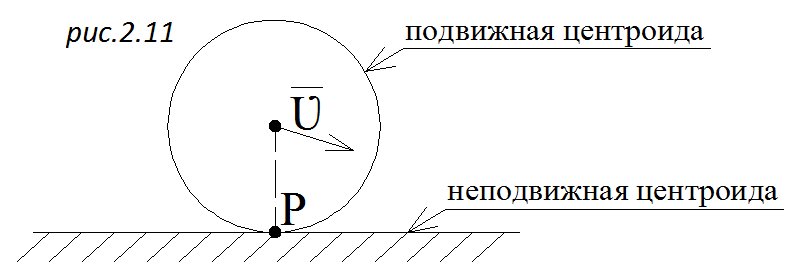
Пример. Круг катится по горизонтальной плоскости без проскальзывания. Свяжем с кругом подвижную плоскость; неподвижная плоскость это плоскость листа. Будем отмечать на них м.ц.с. Получим центроиды (рис 2.11). Плоское движение можно представить как качение подвижной центроиды по неподвижной.
Ускорение точек тела при плоском движении.
Воспользуемся формулой (2.12)
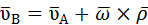
Продифференцируем ее по времени
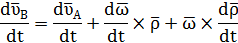
получим
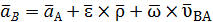
Пусть точка А закреплена, тогда аА=0;
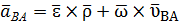
это ускорение точки В во вращательном движении плоской фигуры вокруг полюса А.
Обозначим 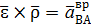 и назовем этот вектор вращательным ускорение точки вокруг полюса А;
и назовем этот вектор вращательным ускорение точки вокруг полюса А; 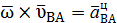 назовем центростремительным ускорение точки В вокруг точки А.
назовем центростремительным ускорение точки В вокруг точки А.
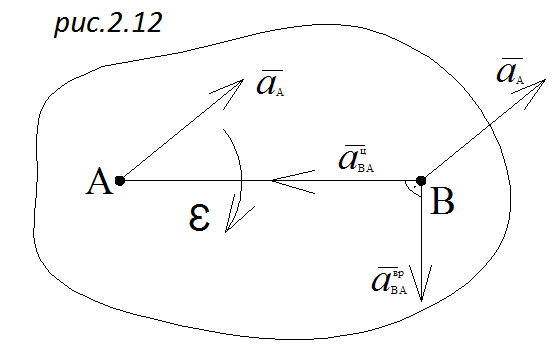
Окончательно получим
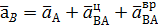 (2.13)
(2.13)
Вектор 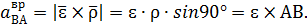 Он направлен перпендикулярно АВ (рис.2.12). Вектор
Он направлен перпендикулярно АВ (рис.2.12). Вектор 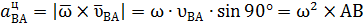 и направлен от В к А.
и направлен от В к А.
Таким образом, ускорение любой точки В плоской фигуры геометрически складывается из ускорения полюса точки А и центростремительного и вращательного ускорений точки В во вращательном движении плоской фигуры относительно полюса А.
Мгновенный центр ускорений
Мгновенным центром ускорений называется точка плоской фигуры, ускорение которой равно нулю.
Пусть известны ускорение точки А – 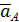 , угловая скорость ω и угловое ускорение ε. Отложим из точки А под углом
, угловая скорость ω и угловое ускорение ε. Отложим из точки А под углом 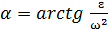 отрезок AQ (рис. 2.13), где
отрезок AQ (рис. 2.13), где
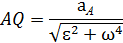
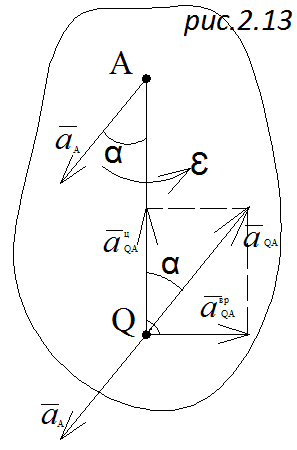
| Определим ускорение точки Q
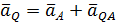
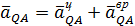 где
где 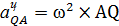 , , 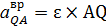 .
Следовательно .
Следовательно
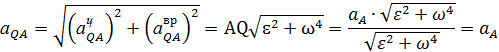
|
Угол между 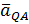 и отрезком
и отрезком 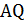
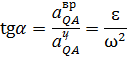
Следовательно, 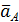 параллельно
параллельно 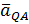 . В точке Q два вектора равны и противоположно направлены,
. В точке Q два вектора равны и противоположно направлены, 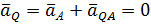
и точка Q – мгновенный центр ускорений. Ускорения всех точек тела пропорциональны расстояниям до мгновенного центра ускорений.
Глава III. Сложное движение точки.
3.1 Основные определения.
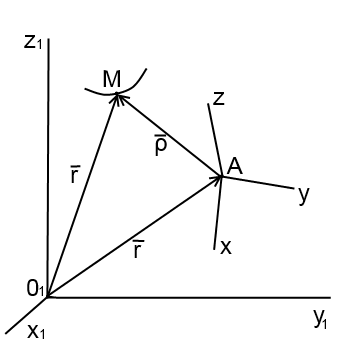
Пусть О1x1y1z1 – неподвижная, основная система координат, Аxyz – подвижная система координат. Точка М движется относительно подвижной системы, а подвижная система координат движется относительно неподвижной системы О1x1y1z1.
Будем называть сложным или абсолютным движением точки ее движение по отношению к системе координат, выбранной за основную.
Движение точки в подвижной системе координат будем называть относительным.
Движение подвижной системы координат относительно неподвижной будем называть переносным движением.
Пусть вектор а задан в подвижной системе координат.
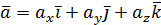
Так как подвижная система движется относительно неподвижной, то 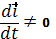
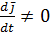
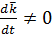
Продифференцируем 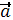 по времени.
по времени.
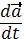 =
= 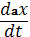
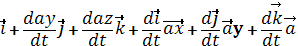 z
z
Обозначим
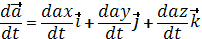 и назовем это выражение локальной производной вектором
и назовем это выражение локальной производной вектором 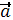 , или производный вектор
, или производный вектор 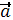 в подвижной системе координат.
в подвижной системе координат.
Так как векторы 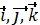 имеют постоянную длину и проведены из начала подвижной системы координат, то по формуле Эйлера (2.6):
имеют постоянную длину и проведены из начала подвижной системы координат, то по формуле Эйлера (2.6):
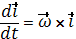
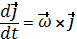
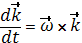
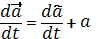 x
x 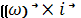 )+ay
)+ay 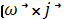 )+ az(
)+ az( 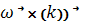 =
= 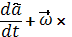 (
( 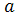 x
x 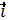 +ay
+ay 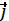 + az
+ az 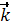 ) =
) = 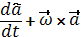
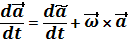 (2.14)
(2.14)
Формула (2.14) называется формулой Бура или производной вектора, заданного в подвижной системе координат.
§ 17. Теорема о сложении скоростей.
Скорость точки M по отношению к основной системе координат назовем абсолютной скоростью, ее обозначения 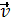 M;
M; 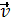 a. ,
a. , 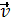
Скорость точки М по отношению подвижной системе назовем относительной скоростью 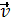 r.
r.
Переносной скоростью называют скорость той точки подвижной системы координат, с которой в данный момент совпадает движущаяся точка М, обозначается 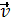 е.
е.
Проведем радиус-векторы 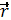 ,
, 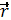 A,
A, 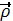 ;
;
где 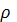 задан в подвижной системе. Продифференцируем
задан в подвижной системе. Продифференцируем 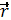 по времени
по времени
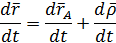
Так как 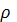 задан в подвижной системе координат, то его производную найдем по формуле Бура.
задан в подвижной системе координат, то его производную найдем по формуле Бура.
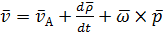 (2.15)
(2.15)
Пусть точка М не движется в подвижной системе. Тогда 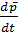 =0 ;
=0 ;
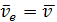 - переносная скорость.
- переносная скорость.
Из формулы (2.15) получим: 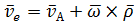
Пусть точка М не движется в подвижной системе координат, тогда 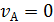 ;
; 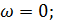
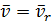 – относительная скорость.
– относительная скорость.
Из формулы (2.15) получим: 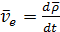
Формула (2.15) принимает вид: 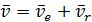 (2.16)
(2.16)
Получили теорему о сложении скоростей точки в сложном движении точки: абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей.
§18. Теорема о сложении ускорений.
Заменим в формуле (2.15) 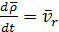
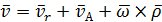 Продифференцируем
Продифференцируем 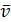 по времени:
по времени:
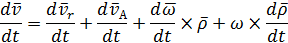
Векторы 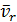 и
и 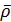 заданы в подвижной системе координат, следовательно, их производную найдём по формуле Бура:
заданы в подвижной системе координат, следовательно, их производную найдём по формуле Бура:
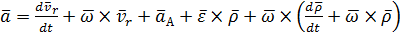 (2.17)
(2.17)
Пусть точка М не движется в подвижной системе, тогда 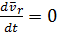 ;
; 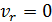 . Т.е. относительное движение отсутствует, остается переносное движение.
. Т.е. относительное движение отсутствует, остается переносное движение.
Получим переносное ускорение, в которое войдут три слагаемых из формулы (2.17).
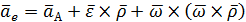
Пусть подвижная система не движется относительно неподвижной, тогда 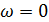 ;
; 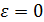 ;
; 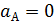 остается относительное движение точки.
остается относительное движение точки.
Из формулы (2.17) получим: 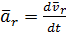
В формуле (2.17) остались два слагаемых, которые не вошли в 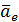 и
и 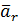
назовём их ускорением Кориолиса: 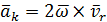
Формула (2.17) принимает вид: 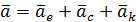 (2/18)
(2/18)
Получена теорема Кориолиса: абсолютное ускорение точки равно геометрической сумме переносного, относительного и ускорения Кориолиса.
Направление ускорения Кориолиса можно определить по правилу векторного произведения или по правилу Жуковского.
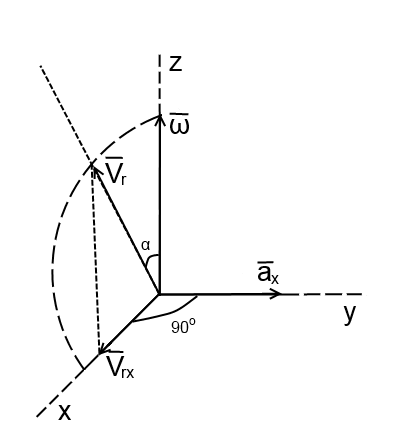 Правило Жуковского: спроецируем
Правило Жуковского: спроецируем 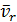 в плоскость перпендикулярную оси переносного вращения и повернём проекцию на 90˚ в сторону
в плоскость перпендикулярную оси переносного вращения и повернём проекцию на 90˚ в сторону 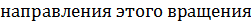 (рис.2.15)
(рис.2.15)
Величина (модуль) ускорения Кориолиса равна 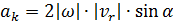
где 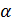 – угол между векторами
– угол между векторами 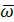 и
и 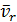
Ускорение 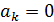 если:
если:
1. 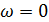 , например, переносное движение - поступательное
, например, переносное движение - поступательное
2. 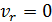
3. 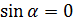 , то есть
, то есть 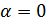 или π, векторы
или π, векторы 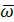 и
и 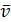 коллинеарны.
коллинеарны.
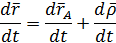
Дата: 2018-12-28, просмотров: 552.