Глава 1. Кинематика точки.
Основные понятия кинематики.
В этом разделе будем изучать движение материальных точек и тел. Под движением тела подразумевают, изменение его положения в пространстве с течением времени. С телом, по отношению к которому изучается движение, связывают систему координатных осей. Время непрерывно, одинаково во всех точках и не зависит от движения тел. Если тело не перемещается по отношению к выбранной системе координат, то говорят, что оно находится в покое. Непрерывную кривую, которую описывает точка в пространстве, называют траекторией точки. Если траектория прямая линия, то движение прямолинейное, кривая линия – криволинейное.
Задачи кинематики: найти способы задания движения точек и тел и для каждого способа определить скорости и ускорения.
1.2. Способы задания движения точки.
Движение точки по отношению к избранной системе координат считается заданным, если известен способ, при помощи которого можно определить положение точки в любой момент времени.
Векторный способ задания движения (рис.1.1)
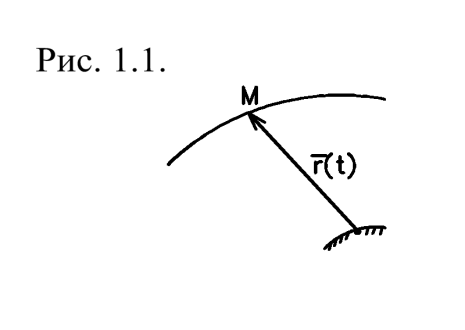
| Положение точки в пространстве будет вполне определено, если задан ее радиус-вектор  (t), проведенный из неподвижного центра. (t), проведенный из неподвижного центра.
 = =  (t) – векторное уравнение движения точки.
Например, (t) – векторное уравнение движения точки.
Например, 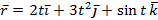
|
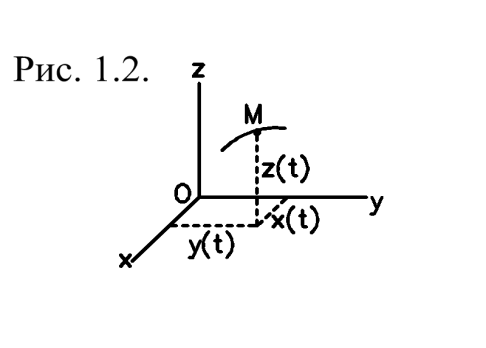
Координатный способ задания движения (рис.1.2)
|
| Положение точки полностью определено заданием координат точки, как функций времени. Например, в декартовой системе координат задаются x = x (t), y = y (t), z = z (t). | ||
|
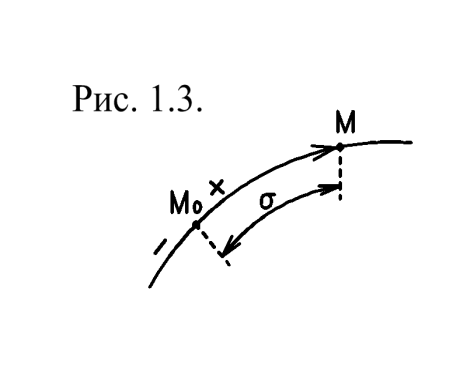
| Естественный способ задания движения (рис.1.3.). В этом случае задаются: траектория точки, начало отсчета Мо, положительное направление отсчета и закон движения по траектории σ = МоМ, т.е. σ = σ (t). Этим способом удобно пользоваться, когда траектория точки заранее известна. | ||
Скорость точки.
Скорость при векторном способе задания движения.
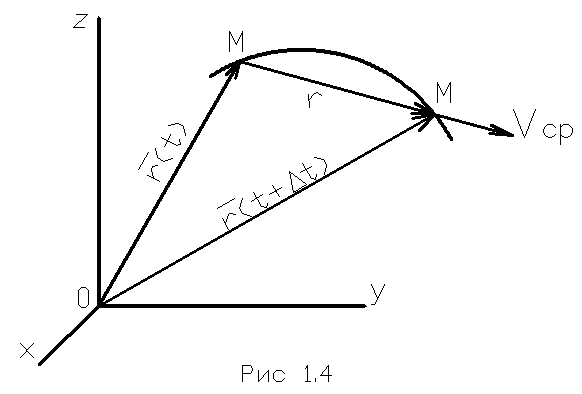
| Пусть в момент t положение точки определяется радиусом – вектором  (t), а в момент t + ∆t радиусом – вектором (t), а в момент t + ∆t радиусом – вектором  (t + ∆t).
Назовем ∆ (t + ∆t).
Назовем ∆  = =  (t + ∆t) – (t + ∆t) –  (t) –вектор перемещения точки за время ∆t. (t) –вектор перемещения точки за время ∆t.
|
Средней скоростью за промежуток времени ∆ t называется вектор 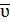 ср=
ср= 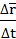 .
.
Скоростью точки в данный момент времени называется предел отношения вектора перемещения точки к промежутку времени, за которое это перемещение произошло, когда этот промежуток времени стремится к нулю.
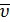 =
= 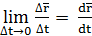 =
=  (1.1)
(1.1)
В системе СИ единица измерения скорости м/с.
Вектор скорости направлен по касательной к траектории в сторону движения.
Скорость при координатном способе задания движения.
Пусть движение точки задано в декартовой системе координат принятой за неподвижную, следовательно, известны x = x(t); y = y(t); z = z(t).
Вектор  можно записать через проекции
можно записать через проекции
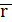 = x·
= x·  + y·
+ y· 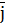 +z·
+z· 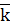
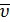 =
= 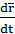 =
= 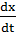 ∙
∙ 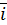 +
+ 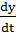 ∙
∙ 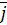 +
+ 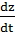 ∙
∙ 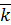 , т.к.
, т.к. 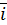 ,
, 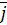 ,
, 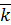 –
– 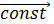 . (1.2)
. (1.2)
Вектор можно записать через проекции
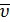 = υx·
= υx· 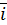 + υy·
+ υy· 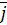 +υz·
+υz· 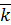 (1.3)
(1.3)
Сравнивая формулы (1.2) и (1.3) получим υx= 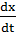 ; υy=
; υy= 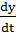 ; υz=
; υz= 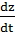 , т.е. проекции скорости на оси равны первой производной от координаты.
, т.е. проекции скорости на оси равны первой производной от координаты.
Модуль скорости υ = 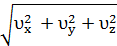
Направляющие косинусы вектора скорости
cos ( 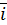 ;
; 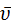 ) =
) = 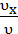
cos ( 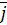 ;
; 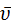 ) =
) = 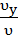
cos ( 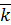 ;
; 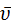 ) =
) = 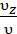
Скорость при естественном способе задания движения.
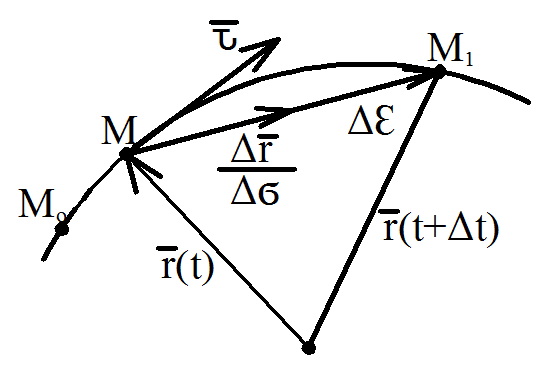 Рис 1.5
Рис 1.5
| Пусть точка М движется по кривой и за время ∆t переместилась из точки М в точку М1 (Рис 1.5). Воспользуемся формулой 1.1 |
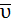 =
= 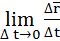 =
= 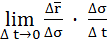 =
= 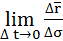 ·
· 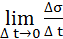 ,
,
где вектор 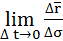 =
= 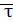 – единичный, направленный по касательной к траектории в точке М в сторону возрастания дуговой координаты..
– единичный, направленный по касательной к траектории в точке М в сторону возрастания дуговой координаты..
По определению производной 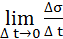 =
= 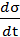 =
= 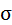 , получим
, получим
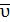 =
= 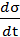 ·
· 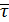 (1.4)
(1.4)
Обозначим 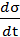 =
= 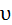 τ – проекция вектора скорости на касательную, тогда
τ – проекция вектора скорости на касательную, тогда
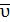 =
= 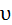 τ ·
τ · 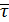 (1.5)
(1.5)
Модуль 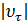 =
= 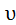 .
.
Ускорение точки.
Ускорение при векторном способе задания движения.
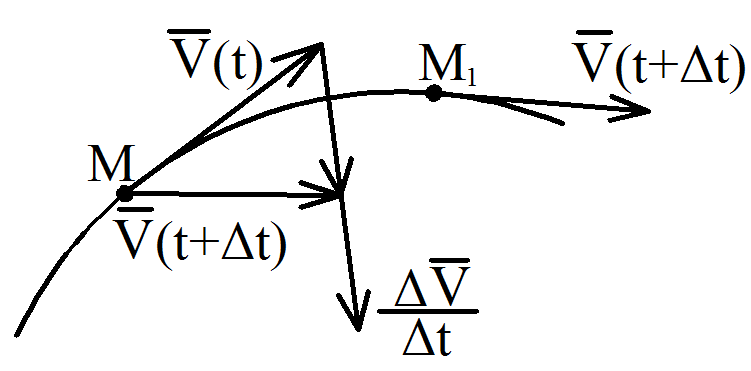 Рис 1.6
Рис 1.6
| Пусть в момент времени t скорость точки М 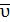 (t) (Рис 1.6), а в момент времени t+∆t скорость (t) (Рис 1.6), а в момент времени t+∆t скорость 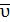 (t+∆t). Изменение вектора скорости за промежуток ∆ t : ∆ (t+∆t). Изменение вектора скорости за промежуток ∆ t : ∆ 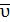 = = 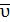 (t+∆t) - (t+∆t) - 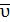 (t) (t)
|
Средним ускорением точки за время ∆t называется вектор 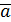 ср= ∆
ср= ∆ 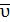 /∆t.
/∆t.
Ускорением точки в данный момент времени называется предел отношения приращения скорости ∆ 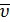 к приращению времени ∆ t при условии ∆ t →0, т.е. производной скорости по времени.
к приращению времени ∆ t при условии ∆ t →0, т.е. производной скорости по времени.
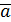 =
= 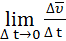 =
= 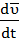 =
= 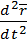 (1.6)
(1.6)
Ускорение при координатном способе задания движения.
Пусть движение точки задано в прямоугольной декартовой системе координат:
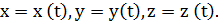
По определению ускорения (1.6)
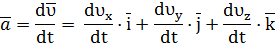
Вектор ускорения можно записать через проекции на оси x, y, z:
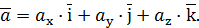
Сравнивая последние формулы , получим:
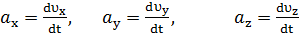 (1.7)
(1.7)
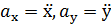 ,
, 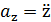 (1.8)
(1.8)
Модуль ускорения 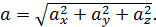
Направляющие косинусы вектора 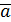 :
:
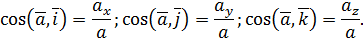
Ускорение при естественном способе задания движения.
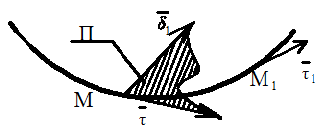 Рис. 1.7
Рис. 1.7 
| Рассмотрим пространственную кривую. Пусть 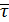 единственный вектор касательной в точке М.
Возьмем близкую точку М1, в ней единственный вектор касательной в точке М.
Возьмем близкую точку М1, в ней 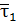 . Перенесем . Перенесем 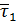 в точку М и проведем плоскость П через в точку М и проведем плоскость П через 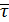 и и 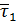 ( Рис.1.7). ( Рис.1.7).
|
Устремим М1 к М.Плоскость П будет поворачиваться вокруг 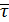 и в пределе займет некоторое положение Ι (Рис. 1.8).
и в пределе займет некоторое положение Ι (Рис. 1.8).
Полученную таким образом плоскость Ι называют соприкасающейся плоскостью к кривой в точке М. Если кривая плоская,то она вся лежит в соприкасающейся плоскости.
Плоскость II,проведенная в точке М перепендикулярно касательной называется нормальной плоскостью (Рис.1.8).
Линия пересечения соприкасающейся и нормальной плоскостей определяет главную нормаль к кривой в точке М, по которой направлен единичный вектор главной нормали 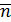 .
.
Плоскость III, проведенную в точке М перпендикулярно главной нормали называют спрямляющей плоскостью (Рис 1.8).
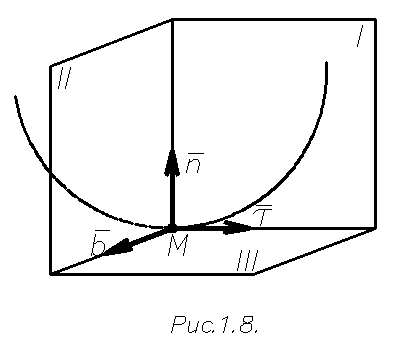
| Линия пересечения спрямляющей и нормальной плоскостей бинормаль к кривой в точке М. Единичный вектор бинормали
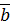 = = 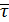 · · 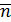 .
Векторы .
Векторы 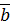 , , 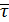 , , 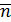 образуют правую тройку векторов. образуют правую тройку векторов.
|
Трехгранник из плоскостей: соприкасающейся, нормальной и спрямляющей, называют естественным трехгранником, а векторы 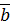 ,
, 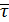 ,
, 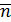 единичными векторами осей естественного трехгранника.
единичными векторами осей естественного трехгранника.
Продифференцируем скорость (1.5) по времени
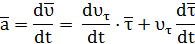
Назовем касательным ускорением вектор:
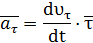
Вектор 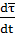 преобразуем
преобразуем
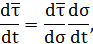
Из математики
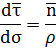
Тогда 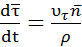
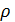 – радиус кривизны траектории в точке М.
– радиус кривизны траектории в точке М.
Назовем нормальным ускорением вектор
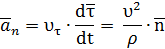
Тогда
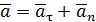 (1.9)
(1.9)
где
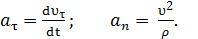 (1.10)
(1.10)
Модуль ускорения
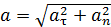 .
.
Если 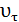 ,
, 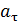 одного знака, то движение называется ускоренным, разно – замедленным.
одного знака, то движение называется ускоренным, разно – замедленным.
Если 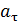 =0, то
=0, то 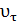 =const – движение называется равномерным.
=const – движение называется равномерным.
Для вычисления касательного ускорения можно использовать равенство
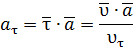
В декартовых координатах
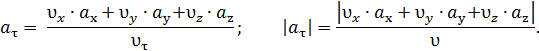
Если 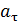 = const, то движение называется равноускоренным или равнозамедленным .
= const, то движение называется равноускоренным или равнозамедленным .
Тогда скорость 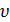 и путь S равны
и путь S равны
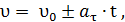
S = 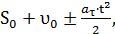
где 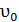 ,
, 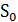 начальные скорости и путь.
начальные скорости и путь.
Задание движения твердого тела.
Основные задачи кинематики твердого тела:
- установление способа задания движения тела;
- изучение кинематических характеристик присущих всему телу;
- определение траекторий, скоростей и ускорений всех точек тела.
Движение тела задано, если есть способ, позволяющий определить положение любой его точки в любой момент времени.
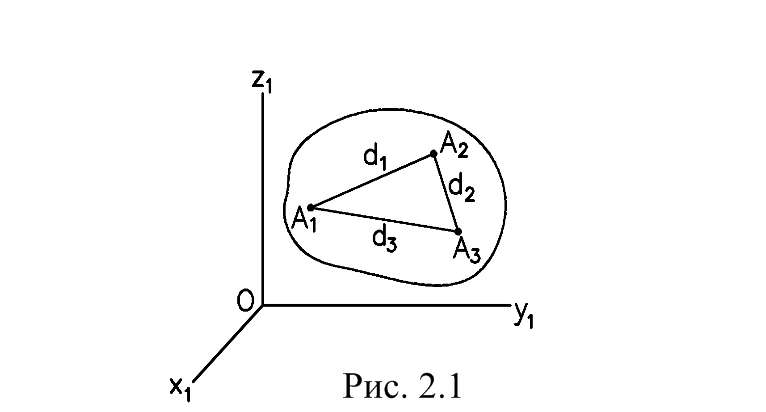
| Положение тела в пространстве полностью определено заданием трех точек А1, А2, А3 с координатами х1, y1, z1;х2, y2, z2;х3, y3, z3. Координаты точек должны удовлетворять трем уравнениям связи (рис. 2.1): |
d21 = (х2 – х1)2 + (у2 – у1)2 + (z2 – z1)2,
d22 = (х3 – х2)2 + (у3 – у2)2 + (z3 – z2)2,
d23 = (х1 – х3)2 + (у1 – у3)2 + (z1 – z3)2.
Следовательно, из девяти координат независимых только шесть.
Число независимых параметров, задание которых однозначно определяет положение твердого тела в пространстве, называется числом степеней свободы твердого тела.
Мгновенный центр ускорений
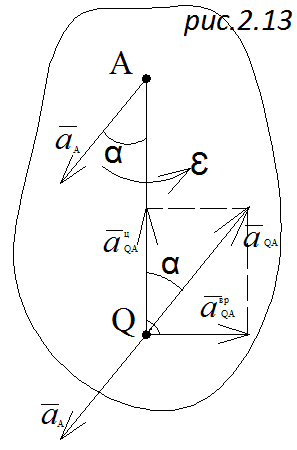
Мгновенным центром ускорений называется точка плоской фигуры, ускорение которой равно нулю.
Пусть известны ускорение точки А – 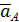 , угловая скорость ω и угловое ускорение ε. Отложим из точки А под углом
, угловая скорость ω и угловое ускорение ε. Отложим из точки А под углом 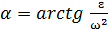 отрезок AQ (рис. 2.13), где
отрезок AQ (рис. 2.13), где
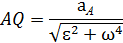
| Определим ускорение точки Q
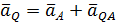
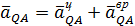 где
где 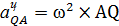 , , 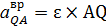 .
Следовательно .
Следовательно
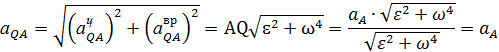
|
Угол между 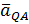 и отрезком
и отрезком 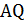
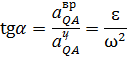
Следовательно, 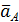 параллельно
параллельно 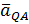 . В точке Q два вектора равны и противоположно направлены,
. В точке Q два вектора равны и противоположно направлены, 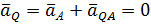
и точка Q – мгновенный центр ускорений. Ускорения всех точек тела пропорциональны расстояниям до мгновенного центра ускорений.
Глава III. Сложное движение точки.
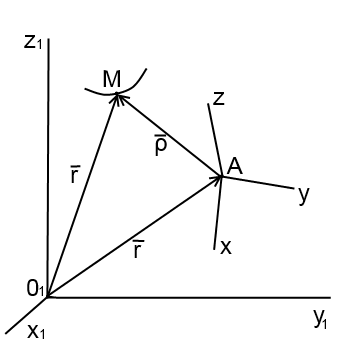
3.1 Основные определения.
Пусть О1x1y1z1 – неподвижная, основная система координат, Аxyz – подвижная система координат. Точка М движется относительно подвижной системы, а подвижная система координат движется относительно неподвижной системы О1x1y1z1.
Будем называть сложным или абсолютным движением точки ее движение по отношению к системе координат, выбранной за основную.
Движение точки в подвижной системе координат будем называть относительным.
Движение подвижной системы координат относительно неподвижной будем называть переносным движением.
Пусть вектор а задан в подвижной системе координат.
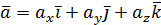
Так как подвижная система движется относительно неподвижной, то 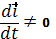
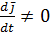
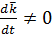
Продифференцируем 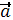 по времени.
по времени.
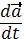 =
= 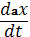
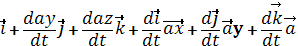 z
z
Обозначим
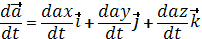 и назовем это выражение локальной производной вектором
и назовем это выражение локальной производной вектором 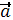 , или производный вектор
, или производный вектор 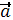 в подвижной системе координат.
в подвижной системе координат.
Так как векторы 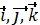 имеют постоянную длину и проведены из начала подвижной системы координат, то по формуле Эйлера (2.6):
имеют постоянную длину и проведены из начала подвижной системы координат, то по формуле Эйлера (2.6):
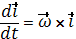
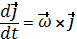
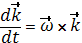
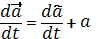 x
x 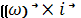 )+ay
)+ay 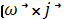 )+ az(
)+ az( 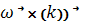 =
= 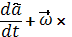 (
( 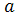 x
x 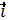 +ay
+ay 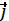 + az
+ az 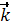 ) =
) = 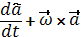
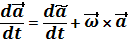 (2.14)
(2.14)
Формула (2.14) называется формулой Бура или производной вектора, заданного в подвижной системе координат.
§ 17. Теорема о сложении скоростей.
Скорость точки M по отношению к основной системе координат назовем абсолютной скоростью, ее обозначения 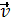 M;
M; 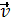 a. ,
a. , 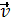
Скорость точки М по отношению подвижной системе назовем относительной скоростью 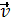 r.
r.
Переносной скоростью называют скорость той точки подвижной системы координат, с которой в данный момент совпадает движущаяся точка М, обозначается 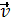 е.
е.
Проведем радиус-векторы 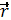 ,
, 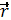 A,
A, 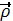 ;
;
где 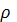 задан в подвижной системе. Продифференцируем
задан в подвижной системе. Продифференцируем 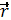 по времени
по времени
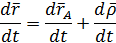
Так как 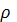 задан в подвижной системе координат, то его производную найдем по формуле Бура.
задан в подвижной системе координат, то его производную найдем по формуле Бура.
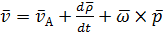 (2.15)
(2.15)
Пусть точка М не движется в подвижной системе. Тогда 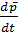 =0 ;
=0 ;
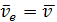 - переносная скорость.
- переносная скорость.
Из формулы (2.15) получим: 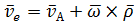
Пусть точка М не движется в подвижной системе координат, тогда 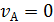 ;
; 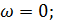
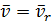 – относительная скорость.
– относительная скорость.
Из формулы (2.15) получим: 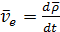
Формула (2.15) принимает вид: 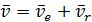 (2.16)
(2.16)
Получили теорему о сложении скоростей точки в сложном движении точки: абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей.
§18. Теорема о сложении ускорений.
Заменим в формуле (2.15) 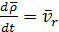
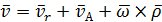 Продифференцируем
Продифференцируем 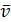 по времени:
по времени:
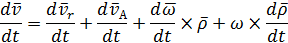
Векторы 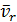 и
и 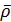 заданы в подвижной системе координат, следовательно, их производную найдём по формуле Бура:
заданы в подвижной системе координат, следовательно, их производную найдём по формуле Бура:
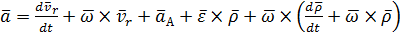 (2.17)
(2.17)
Пусть точка М не движется в подвижной системе, тогда 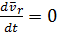 ;
; 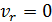 . Т.е. относительное движение отсутствует, остается переносное движение.
. Т.е. относительное движение отсутствует, остается переносное движение.
Получим переносное ускорение, в которое войдут три слагаемых из формулы (2.17).
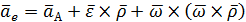
Пусть подвижная система не движется относительно неподвижной, тогда 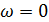 ;
; 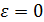 ;
; 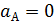 остается относительное движение точки.
остается относительное движение точки.
Из формулы (2.17) получим: 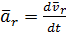
В формуле (2.17) остались два слагаемых, которые не вошли в 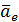 и
и 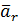
назовём их ускорением Кориолиса: 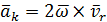
Формула (2.17) принимает вид: 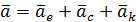 (2/18)
(2/18)
Получена теорема Кориолиса: абсолютное ускорение точки равно геометрической сумме переносного, относительного и ускорения Кориолиса.
Направление ускорения Кориолиса можно определить по правилу векторного произведения или по правилу Жуковского.
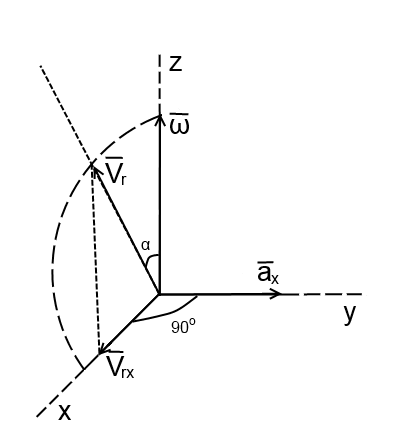 Правило Жуковского: спроецируем
Правило Жуковского: спроецируем 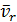 в плоскость перпендикулярную оси переносного вращения и повернём проекцию на 90˚ в сторону
в плоскость перпендикулярную оси переносного вращения и повернём проекцию на 90˚ в сторону 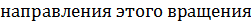 (рис.2.15)
(рис.2.15)
Величина (модуль) ускорения Кориолиса равна 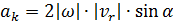
где 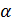 – угол между векторами
– угол между векторами 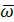 и
и 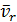
Ускорение 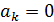 если:
если:
1. 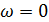 , например, переносное движение - поступательное
, например, переносное движение - поступательное
2. 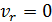
3. 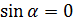 , то есть
, то есть 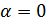 или π, векторы
или π, векторы 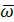 и
и 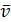 коллинеарны.
коллинеарны.
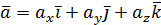
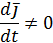
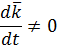
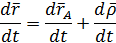
Глава 1. Кинематика точки.
Основные понятия кинематики.
В этом разделе будем изучать движение материальных точек и тел. Под движением тела подразумевают, изменение его положения в пространстве с течением времени. С телом, по отношению к которому изучается движение, связывают систему координатных осей. Время непрерывно, одинаково во всех точках и не зависит от движения тел. Если тело не перемещается по отношению к выбранной системе координат, то говорят, что оно находится в покое. Непрерывную кривую, которую описывает точка в пространстве, называют траекторией точки. Если траектория прямая линия, то движение прямолинейное, кривая линия – криволинейное.
Задачи кинематики: найти способы задания движения точек и тел и для каждого способа определить скорости и ускорения.
1.2. Способы задания движения точки.
Движение точки по отношению к избранной системе координат считается заданным, если известен способ, при помощи которого можно определить положение точки в любой момент времени.
Векторный способ задания движения (рис.1.1)

| Положение точки в пространстве будет вполне определено, если задан ее радиус-вектор  (t), проведенный из неподвижного центра. (t), проведенный из неподвижного центра.
 = =  (t) – векторное уравнение движения точки.
Например, (t) – векторное уравнение движения точки.
Например, 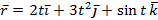
|
Координатный способ задания движения (рис.1.2)
|
| Положение точки полностью определено заданием координат точки, как функций времени. Например, в декартовой системе координат задаются x = x (t), y = y (t), z = z (t). | ||
|
| Естественный способ задания движения (рис.1.3.). В этом случае задаются: траектория точки, начало отсчета Мо, положительное направление отсчета и закон движения по траектории σ = МоМ, т.е. σ = σ (t). Этим способом удобно пользоваться, когда траектория точки заранее известна. | ||
Скорость точки.
Скорость при векторном способе задания движения.

| Пусть в момент t положение точки определяется радиусом – вектором  (t), а в момент t + ∆t радиусом – вектором (t), а в момент t + ∆t радиусом – вектором  (t + ∆t).
Назовем ∆ (t + ∆t).
Назовем ∆  = =  (t + ∆t) – (t + ∆t) –  (t) –вектор перемещения точки за время ∆t. (t) –вектор перемещения точки за время ∆t.
|
Средней скоростью за промежуток времени ∆ t называется вектор 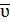 ср=
ср= 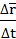 .
.
Скоростью точки в данный момент времени называется предел отношения вектора перемещения точки к промежутку времени, за которое это перемещение произошло, когда этот промежуток времени стремится к нулю.
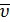 =
= 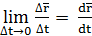 =
=  (1.1)
(1.1)
В системе СИ единица измерения скорости м/с.
Вектор скорости направлен по касательной к траектории в сторону движения.
Скорость при координатном способе задания движения.
Пусть движение точки задано в декартовой системе координат принятой за неподвижную, следовательно, известны x = x(t); y = y(t); z = z(t).
Вектор  можно записать через проекции
можно записать через проекции
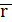 = x·
= x·  + y·
+ y· 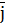 +z·
+z· 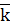
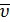 =
= 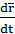 =
= 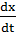 ∙
∙ 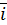 +
+ 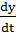 ∙
∙ 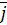 +
+ 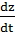 ∙
∙ 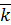 , т.к.
, т.к. 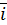 ,
, 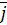 ,
, 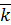 –
– 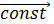 . (1.2)
. (1.2)
Вектор можно записать через проекции
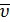 = υx·
= υx· 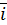 + υy·
+ υy· 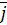 +υz·
+υz· 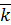 (1.3)
(1.3)
Сравнивая формулы (1.2) и (1.3) получим υx= 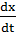 ; υy=
; υy= 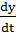 ; υz=
; υz= 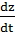 , т.е. проекции скорости на оси равны первой производной от координаты.
, т.е. проекции скорости на оси равны первой производной от координаты.
Модуль скорости υ = 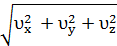
Направляющие косинусы вектора скорости
cos ( 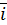 ;
; 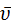 ) =
) = 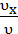
cos ( 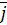 ;
; 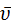 ) =
) = 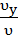
cos ( 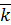 ;
; 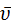 ) =
) = 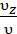
Скорость при естественном способе задания движения.
 Рис 1.5
Рис 1.5
| Пусть точка М движется по кривой и за время ∆t переместилась из точки М в точку М1 (Рис 1.5). Воспользуемся формулой 1.1 |
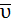 =
= 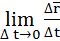 =
= 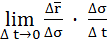 =
= 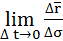 ·
· 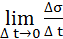 ,
,
где вектор 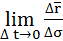 =
= 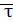 – единичный, направленный по касательной к траектории в точке М в сторону возрастания дуговой координаты..
– единичный, направленный по касательной к траектории в точке М в сторону возрастания дуговой координаты..
По определению производной 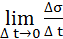 =
= 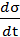 =
= 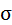 , получим
, получим
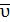 =
= 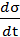 ·
· 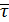 (1.4)
(1.4)
Обозначим 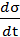 =
= 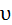 τ – проекция вектора скорости на касательную, тогда
τ – проекция вектора скорости на касательную, тогда
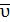 =
= 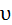 τ ·
τ · 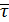 (1.5)
(1.5)
Модуль 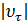 =
= 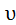 .
.
Ускорение точки.
Ускорение при векторном способе задания движения.
 Рис 1.6
Рис 1.6
| Пусть в момент времени t скорость точки М 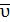 (t) (Рис 1.6), а в момент времени t+∆t скорость (t) (Рис 1.6), а в момент времени t+∆t скорость 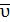 (t+∆t). Изменение вектора скорости за промежуток ∆ t : ∆ (t+∆t). Изменение вектора скорости за промежуток ∆ t : ∆ 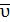 = = 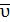 (t+∆t) - (t+∆t) - 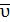 (t) (t)
|
Средним ускорением точки за время ∆t называется вектор 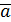 ср= ∆
ср= ∆ 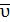 /∆t.
/∆t.
Ускорением точки в данный момент времени называется предел отношения приращения скорости ∆ 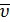 к приращению времени ∆ t при условии ∆ t →0, т.е. производной скорости по времени.
к приращению времени ∆ t при условии ∆ t →0, т.е. производной скорости по времени.
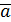 =
= 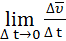 =
= 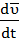 =
= 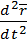 (1.6)
(1.6)
Ускорение при координатном способе задания движения.
Пусть движение точки задано в прямоугольной декартовой системе координат:
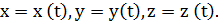
По определению ускорения (1.6)
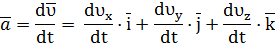
Вектор ускорения можно записать через проекции на оси x, y, z:
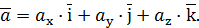
Сравнивая последние формулы , получим:
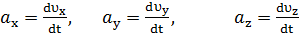 (1.7)
(1.7)
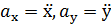 ,
, 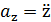 (1.8)
(1.8)
Модуль ускорения 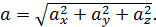
Направляющие косинусы вектора 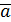 :
:
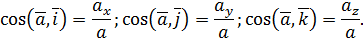
Ускорение при естественном способе задания движения.
 Рис. 1.7
Рис. 1.7 
| Рассмотрим пространственную кривую. Пусть 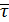 единственный вектор касательной в точке М.
Возьмем близкую точку М1, в ней единственный вектор касательной в точке М.
Возьмем близкую точку М1, в ней 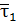 . Перенесем . Перенесем 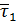 в точку М и проведем плоскость П через в точку М и проведем плоскость П через 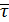 и и 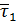 ( Рис.1.7). ( Рис.1.7).
|
Устремим М1 к М.Плоскость П будет поворачиваться вокруг 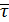 и в пределе займет некоторое положение Ι (Рис. 1.8).
и в пределе займет некоторое положение Ι (Рис. 1.8).
Полученную таким образом плоскость Ι называют соприкасающейся плоскостью к кривой в точке М. Если кривая плоская,то она вся лежит в соприкасающейся плоскости.
Плоскость II,проведенная в точке М перепендикулярно касательной называется нормальной плоскостью (Рис.1.8).
Линия пересечения соприкасающейся и нормальной плоскостей определяет главную нормаль к кривой в точке М, по которой направлен единичный вектор главной нормали 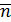 .
.
Плоскость III, проведенную в точке М перпендикулярно главной нормали называют спрямляющей плоскостью (Рис 1.8).

| Линия пересечения спрямляющей и нормальной плоскостей бинормаль к кривой в точке М. Единичный вектор бинормали
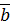 = = 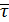 · · 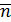 .
Векторы .
Векторы 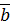 , , 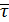 , , 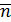 образуют правую тройку векторов. образуют правую тройку векторов.
|
Трехгранник из плоскостей: соприкасающейся, нормальной и спрямляющей, называют естественным трехгранником, а векторы 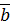 ,
, 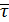 ,
, 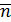 единичными векторами осей естественного трехгранника.
единичными векторами осей естественного трехгранника.
Продифференцируем скорость (1.5) по времени
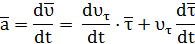
Назовем касательным ускорением вектор:
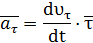
Вектор 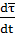 преобразуем
преобразуем
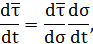
Из математики
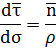
Тогда 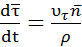
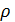 – радиус кривизны траектории в точке М.
– радиус кривизны траектории в точке М.
Назовем нормальным ускорением вектор
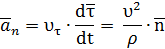
Тогда
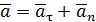 (1.9)
(1.9)
где
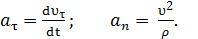 (1.10)
(1.10)
Модуль ускорения
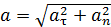 .
.
Если 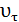 ,
, 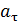 одного знака, то движение называется ускоренным, разно – замедленным.
одного знака, то движение называется ускоренным, разно – замедленным.
Если 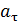 =0, то
=0, то 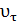 =const – движение называется равномерным.
=const – движение называется равномерным.
Для вычисления касательного ускорения можно использовать равенство
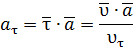
В декартовых координатах
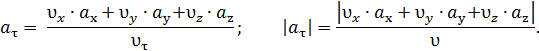
Если 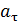 = const, то движение называется равноускоренным или равнозамедленным .
= const, то движение называется равноускоренным или равнозамедленным .
Тогда скорость 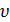 и путь S равны
и путь S равны
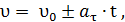
S = 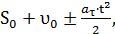
где 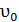 ,
, 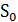 начальные скорости и путь.
начальные скорости и путь.
Движение точки по окружности.
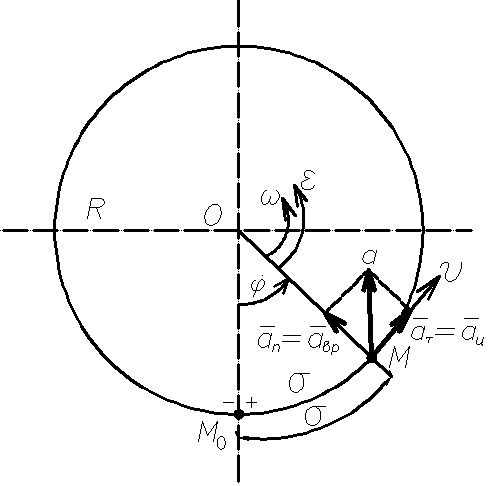
| Пусть точка М движется по окружности радиуса R. Положение точки М зададим дуговой координатой 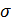 : : 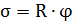 .
По формуле (1.5) .
По формуле (1.5)
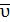 = = 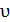 τ· τ· 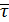 где
где 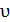 τ = τ = 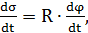
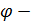 угол поворота радиуса ОМ. угол поворота радиуса ОМ.
|
Обозначим 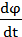 =
= 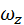 и называется угловой скоростью вращения радиуса ОМ.
и называется угловой скоростью вращения радиуса ОМ.
Тогда 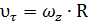
Вектор скорости направлен по касательной к окружности. По формулам (1.9) и (1.10)
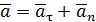
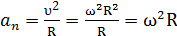 – нормальное ускорение направленно по главной нормали к центру О, его называют центростремительным ускорением.
– нормальное ускорение направленно по главной нормали к центру О, его называют центростремительным ускорением.
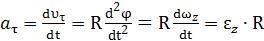 – касательное ускорение, направлено по касательной к окружности,
– касательное ускорение, направлено по касательной к окружности,
где 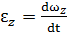 называют угловым ускорением радиуса ОМ,
называют угловым ускорением радиуса ОМ,
ускорение 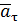 называют вращательным. Так как
называют вращательным. Так как 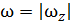 , окончательно получим
, окончательно получим
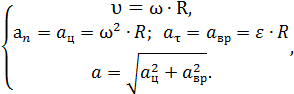 (1.11)
(1.11)
Дата: 2018-12-28, просмотров: 395.