Пусть тело имеет две неподвижные точки А и В. Тогда все точки на прямой
АВ неподвижны. Прямая АВ называется осью вращения, движение тела называется вращательным. Все точки тела описывают окружности с центрами на оси АВ.
Положение тела определяется одним параметром - углом поворота φ тела между подвижной плоскостью П1, жестко связанной с телом, и неподвижной плоскостью П2 (рис. 2.3).
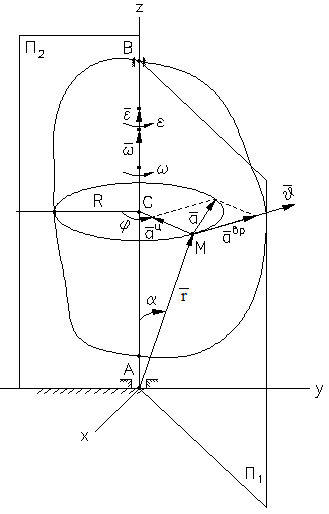 Рис 2.3 Рис 2.3
| Пусть в момент времени t угол между плоскостями равен φ(t), а в момент времени t + ∆t – φ(t + ∆t). Следовательно, за время ∆t тело повернулось на угол ∆φ = φ(t + ∆t) – φ(t).
Средняя угловая скорость за промежуток времени ∆t: ωz,ср = 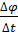 .
Угловая скорость тела в данный момент времени равна: .
Угловая скорость тела в данный момент времени равна:
|
ωz = 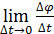 =
= 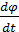 =
= 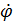 . (2.2)
. (2.2)
Модуль угловой скорости обозначим
ω = 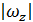 =
= 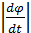 .
.
Единица измерения угловой скорости 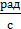 или
или  .
.
Зависимость между угловой скоростью ω и n – числом оборотов в минуту
ω = 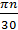 .
.
Угловую скорость можно представить как вектор 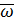 , модуль которого равен ω и направлен по оси вращения в ту сторону, откуда вращение тела видно против часовой стрелки.
, модуль которого равен ω и направлен по оси вращения в ту сторону, откуда вращение тела видно против часовой стрелки.
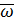 = ωz ∙
= ωz ∙ 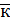 (2.3)
(2.3)
Пусть в момент времени t угловая скорость вращения ωz(t), а в момент t + ∆t равна ωz (t + ∆t). Приращение угловой скорости за промежуток времени ∆t равно:
∆ωz = ωz (t + ∆t) – ωz(t).
Средним угловым ускорением за время ∆t будем называть
εz,ср = 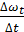 .
.
Угловым ускорением в данный момент времени называется
εz = 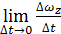 =
= 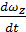 =
= 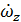 =
= 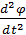 =
=  (2.4)
(2.4)
Модуль углового ускорения обозначим
ε = 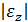 .
.
Единица измерения углового ускорения - 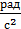 ,
, 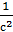 .
.
Вектором углового ускорения будем называть вектор
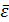 =
= 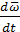 = εz ∙
= εz ∙ 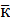
Если ωz и εz одного знака, то они направлены в одну сторону и движение называют ускоренным, разных знаков – замедленным. Если ε = const, то вращение тела называют равноускоренным или равнозамедленным и формулы для ω и φ имеют вид:
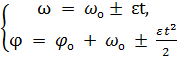 (2.5)
(2.5)
где ωo – начальная угловая скорость тела, φо – начальный угол поворота тела.
Пусть  – вектор, проведенный из точки А в точку М (рис. 2.3). Тогда скорость точки М тела можно выразить формулой Эйлера
– вектор, проведенный из точки А в точку М (рис. 2.3). Тогда скорость точки М тела можно выразить формулой Эйлера
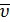 =
= 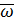 х
х  .
.
По правилу векторного произведения вектор 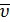 направлен перпендикулярно
направлен перпендикулярно 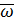 и
и  , т.е. по касательной к траектории движения точки М. По модулю
, т.е. по касательной к траектории движения точки М. По модулю
υ = ω ∙ r ∙ sinα = υ = ω ∙ R,
где R= СМ – радиус окружности.
Продифференцируем (2.6)по времени
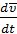 =
= 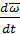 х
х  +
+ 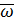 х
х 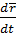 .
.
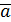 =
= 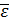 х
х  +
+ 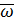 х
х 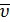 ,
,
где 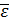 =
= 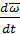 ,
, 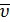 =
= 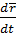 .
.
Вращательное ускорение 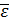 х
х  =
= 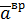 ;
;
по модулю авр = ε ∙ r∙sinα = ε∙R.
Центростремительное ускорение 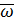 х
х 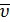 =
= 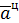 ;
;
по модулю ац = ω ∙ υ ∙ sin900 = ω ∙ ω ∙ r = ω2∙R.
Направление 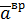 и
и 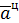 определяется правилом векторного произведения и указано на (рис. 2.3).
определяется правилом векторного произведения и указано на (рис. 2.3).
Модуль ускорения точки М равен
а = 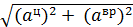 . (2.8)
. (2.8)
2.4. Плоское движение тела: определение, задание движения.
Движение тела называют плоским, если все точки тела перемещаются в плоскостях, параллельных некоторой неподвижной плоскости.
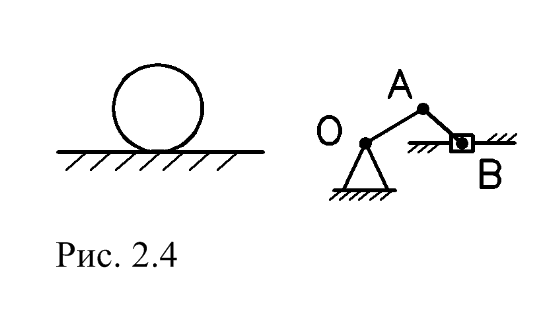
| Например: Плоское движение совершает колесо на прямолинейном участке, шатун АВ кривошипно-шатунного механизма (рис. 2.4). | |
|
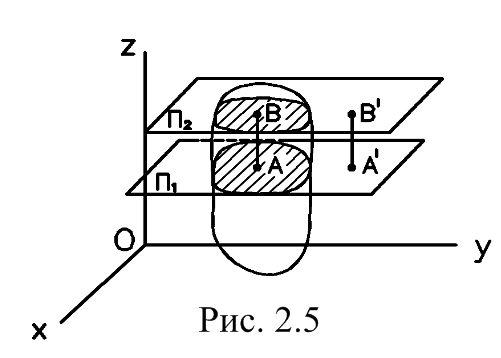
| Пусть все точки и тела движутся в плоскостях параллельных плоскости хОу (рис. 2.5). Проведем плоскости П1 и П2 параллельно хОу. Проведем прямую перпендикулярно П1 и П2. Получим точки А и В. АВ – кратчайшее расстояние | |
между плоскостями. При движении точки А и В не выйдут из плоскостей П1 и П2, следовательно, А'В'||AB, т.е. отрезок АВ движется поступательно. Таким образом, вместо изучения движения прямой АВ можно изучать только движение точки А, а вместо изучения движения тела, можно изучать движение только одного сечения. Задание движения тела сводится к заданию движения сечения.
Плоское движение можно представить как сумму поступательного и вращательного движений. Пусть плоская фигура переместилась из положения I в положение II.
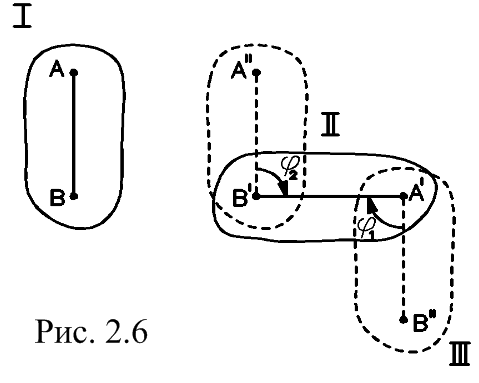
| Отрезок АВ занял положение А'В'. Представим это перемещение как сумму движений. Переместим фигуру из положения I в положение III поступательно, так, чтобы точки А и А' совпали и повернем её на угол φ1 вокруг точки А'. Получим положение II (рис. 2.6). Переместим фигуру из положения I в |
положение IV поступательно, так, чтобы точки В и В' совпали и повернем её на угол φ2 вокруг точки В'. Получим положение II. Очевидно, что φ1=φ2, следовательно, поступательное движение зависит от выбора полюса, а вращательное не зависит.
Пусть О1х1у1 – неподвижная система координат, Ах2у2 – подвижная система координат, движущаяся поступательно относительно неподвижной.
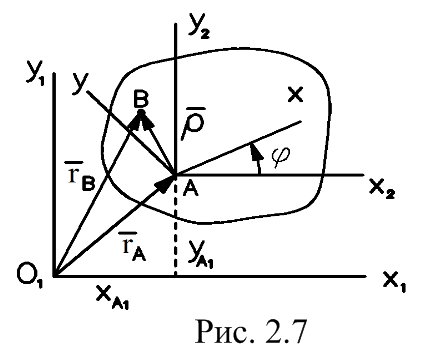
| Свяжем с плоской фигурой систему координат Аху. Положение плоской фигуры определится тремя параметрами: координатами точки А и углом поворота φ. х1А= х1А(t); у1А= у1А(t); φ=φ(t) (2.9) Равенства (2.9) называются уравнениями движения плоской фигуры. |
Дата: 2018-12-28, просмотров: 362.