Решение задачи на построение обычно включает четыре этапа:

анализ, построение, доказательство и исследование. Рассмотрим каж­дый из них в отдельности.

1. Анализ. На этом этапе осуществляется поиск решения задачи. Его конечная цель - установление последовательности, алгоритма, состоящего из основных или элементарных построений, приводящих к построению искомой фигуры. Как и решение геометрической задачи на вычисление и доказательство, поиск такого алгоритма сопровож­дается чертежом, иллюстрацией, помогающими установить связи и зависимости между данными и искомыми фигурами.

2. Построение. Этот этап решения представляет собой непосредст­венную реализацию на чертеже найденного алгоритма с помощью выбранных инструментов построения.

3. Доказательство. Его цель - доказательство того, что построен­ная на предыдущем этапе фигура действительно искомая, т.е. удовле­творяет всем поставленным в задаче условиям.

4. Исследование. Этот этап решения состоит в выяснении того, всег­да ли задача имеет решение; если не всегда, то при каких конкретных данных и сколько именно решений она имеет. При этом разными счи­таются решения, дающие неравные фигуры (или если и равные, то различно расположенные относительно фигуры, с которой связыва­лось построение).

Проиллюстрируем эти этапы на конкретном примере.

Задача. Построить параллелограмм по ос­нованию а, высоте h и одной из диагоналей d.

Согласно условию, данными являются отрез­ки, представляющие основание, высоту и диагональ параллелограмма (рис.). Все эти фигуры считаются уже построенными, и поэтому объяснение не требуется.                      

1. Анализ. Выполним чертеж-иллюстрацию, считая, что иско­мый параллелограмм АВС D уже построен (рис.). Отмечаем на чертеже данные элементы: ВС = а, ВН = h, DВ= d.

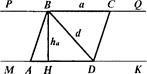
Устанавливаем связи и зависимости между элементами параллелограмма. От­мечаем, что противоположные стороны АВ и DС лежат на параллельных прямых, расстояние между которыми равно высоте h. Поэтому можно построить треугольник АВ D и затем достроить его до параллело­грамма АВС D. Получим следующий алгоритм построения искомой фигуры:

1) Строим параллельные прямые МК и Р Q на расстоянии h друг от друга.

2) На прямой МК откладываем отрезок А D = а.

3) Из точки D, как из центра, радиусом d проводим окружность и находим точку В ее пересечения с прямой Р Q.

4) На луче В Q откладываем отрезок ВС = а.

5) Строим отрезки АВ и С D.

2. Построение. Все этапы алгоритма построения выполняем циркулем и линейкой непосредственно на чертеже с использованием заданных элементов (рис. 157).

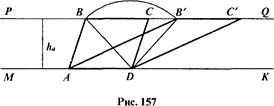
3. Доказательство. Рассмотрим четырехугольник АВС D. Его противоположные стороны А D и ВС параллельны, так как лежат на па­раллельных прямых МК и Р Q. Эти же стороны равны по построению:

А D = ВС = а. Значит, АВС D - параллелограмм, у которого А D = а, В D = d, а высота равна h, так как расстояние между параллельными прямыми МК и Р Q равно h (по построению). Следовательно, АВС D -искомый параллелограмм.

4. Исследование. Проверим возможность построения паралле­лограмма АВС D  непосредственно по шагам алгоритма построения.

1) Параллельные прямые МК и Р Q на расстоянии h  всегда можно построить, и притом единственным образом.

2) Построить отрезок А D = а на прямой МК также всегда можно, и притом единственным образом.

3) Окружность, проведенная из центра D радиусом d, будет иметь общие точки с прямой Р Q только тогда, когда d ≥ h. Если d = h, то по­лучится одна общая точка В, если же d > h, то две общие точки В и В'.

 5) Эти построения всегда однозначно выполнимы. Таким образом, решение возможно, если d ≥ h. Если d = h, то зада­ча имеет единственное решение, если же d > h, то два решения.

Упражнения

1. Постройте с помощью циркуля и линейки треугольник по из­вестным трем сторонам. Всегда ли такое построение возможно?

2. Даны отрезок р, два угла α и β. Всегда ли можно построить тре­угольник, у которого сторона равна р, а прилежащие к ней углы рав­ны α и β.

3. Постройте с помощью циркуля и линейки прямоугольник, у ко­торого известны его стороны а и в.

4. Пользуясь только циркулем и линейкой, постройте:

а) прямоугольник по диагонали и одной из сторон;

б) квадрат со стороной р;

в) квадрат, диагональ которого задана.

5. Сколько можно построить параллелограммов с вершинами в трех данных точках, не лежащих на одной прямой?

6. Постройте параллелограмм, если известны его диагонали и угол между ними.

7. Сколько параллелограммов можно построить, если известны две его соседние стороны? Ответ обоснуйте.

8. С помощью циркуля и линейки постройте ромб по:

а) известным диагоналям;

б) известной стороне и одному из углов при его вершине;

в) углу и диагонали, исходящей из вершины этого угла;

г) стороне и диагонали.

9. Постройте трапецию по основаниям и боковым сторонам.

10. По каким данным можно построить равнобедренный треуголь­ник? Во всех возможных случаях выполните построения.

3. Методы решения задач на построение: преобразования геометрических фигур на плоскости: центральная, осевая симметрии, гомотетия, движение.

Пусть на плоскости (в пространстве) задана фигура F. Поставим в соответствие каждой точке данной фигуры F единственную точку плоскости (пространства). Получим новую фигуру F'. В этом случае говорят, что фигура F' получена преобразованием фигуры F. При этом фигура F' является образом фигуры F для данного преобразования, а фигуры F – прообразом фигуры F'. Существует несколько видов преобразований: симметрия относительно точки (центральная симметрия), симметрия относительно прямой (осевая симметрия), симметрия относительно плоскости, гомотетия и др.

Симметрия относительно точки. Пусть О – фиксированная точка и Х – произвольная точка. Точка Х ' называется симметричной точке Х относительно точки О, если точки Х, О, Х' лежат на одной прямой и ОХ = О Х '. Точка, симметричная  точке Х ', есть точка Х. Преобразование фигуры F в фигуру F', при котором каждая ее точка Х переходит в точку Х', симметричную Х относительно данной точки О, называется преобразованием симметрии относительно точки О.

Если преобразование симметрии относительно точки О переводит фигуру F в себя, то фигура называется центрально-симметричной относительно точки О, а точка О – ее центром симметрии. Примеры – параллелограмм, окружность, куб, сфера, параллелепипед.

Пусть m – фиксированная прямая и Х – произвольная точка. Точка Х ' называется симметричной точке Х относительно прямой m, если прямая ХХ' перпендикулярна прямой m и  ОХ = О Х ', где точка О – точка пересечения прямых ХХ' и m. Точка, симметричная точке Х , лежащей на прямой m, есть сама точка Х. Точка, симметричная точке Х ', есть точка Х. Преобразование фигуры F в фигуру F', при котором каждая ее точка Х переходит в точку Х', симметричную Х относительно данной прямой m, называется преобразованием симметрии относительно прямой m. Прямая m называется осью симметрии.

Гомотетия. Пусть F – данная фигура и О – фиксированная точка. Проведем через произвольную точку Х фигуры F луч ОХ и отложим на нем отрезок ОХ', равный k∙ОХ, где k – положительное число. Преобразование фигуры F в фигуру F', при котором каждая ее точка Х переходит в такую точку Х', что ОХ = k∙ОХ', называется гомотетией относительно центра О, число k называется коэффициентом гомотетии. Фигуры F и F' называются гомотетичными.

Движение – преобразование фигуры F в фигуру F', при котором сохраняется расстояние между точками, т.е. движение переводит любые две точки Х и Y фигуры F в точки Х ' и Y' фигуры F' так, что ХY = Х 'Y'.

Преобразование симметрии относительно точки является движением (центральная симметрия).

Преобразование симметрии относительно прямой является движением (осевая симметрия).

Преобразование симметрии относительно плоскости является движением.

Основные выводы

Рассмотрев материал данного параграфа, выяснили, что построе­ние геометрических фигур с заданными свойствами при помощи цир­куля и линейки осуществляется по определенным правилам. Прежде всего, надо знать, какие построения можно выполнять с помощью линейки, не имеющей делений, и с помощью циркуля. Эти построения называют основными. Кроме того, надо уметь решать элементарные задачи на построение, т.е. уметь строить: отрезок, равный данному; угол, равный данному; середину отрезка; биссектрису угла; прямую, перпендикулярную данной прямой, и проходящую через данную точку.

Процесс решения более сложных задач на построение разбивается на 4 этапа и основывается на умении решать элементарные задачи.