Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Приращения координат находят по дирекционным углам и длинам сторон хода.

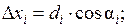
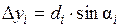.             (2.8)

Результаты заносят в графы 6 и 7, округляя полученные величины до сантиметров (два знака после запятой).

Следующий этап обработки предусматривает вычисление невязок в приращениях координат и определения их допустимости. Невязки получают по формулам:

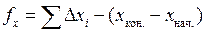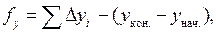;      (2.9)

где х_нач, у_нач, х_кон, у_кон − координаты начальной и конечной точек теодолитного хода.

Для нашего примера

.

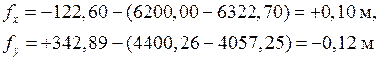Затем вычисляют абсолютную невязку теодолитного хода:

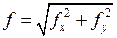                                                                            (2.10)

и относительную невязку теодолитного хода:

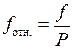             ,                                        (2.11)

где P − длина хода.

В соответствии с Инструкцией по выполнению топографической съемки относительная невязка в теодолитном ходе не должна превышать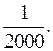

В нашем примере

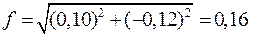м;

.

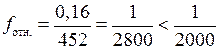Если относительная невязка окажется больше допустимой, то в расчетно-графической работе это указывает на наличие ошибок в вычислении приращений координат. Ошибки следует обнаружить и устранить1.

Если полученная относительная невязка не превосходит 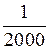, то выполняют уравнивание, распределяя невязки f _x и f _y, вводя поправки в приращения координат пропорционально длинам сторон со знаком, противоположным знаку соответствующей невязки:

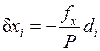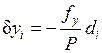                   ; ,                                                            (2.12)

где d_i − длина соответствующей стороны хода;

P − длина хода.

Вычисленные поправки округляют до 0,01 м и подписывают над соответствующими значениями Dx_i и Dy_i  в графы 6 и 7 табл. 1.

Суммы поправок должны быть равны соответствующим невязкам с противоположным знаком, то есть должны соблюдаться равенства

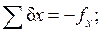
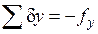              .                                        (2.13)

Равенство (2.13) может не соблюдаться за счет округления поправок. В этом случае поправки можно несколько изменить, добившись выполнения равенства (2.13).

Поправками исправляют приращения координат

               Dx_i¢ = Dx_i + dx_i; Dу _i¢ = Dy_i + dy_i.                      (2.14)

В нашем случае для стороны I−II имеем

                   Dx ¢_I-II = +76,67 – 0,03 = +76,64 м;

                   Dy ¢_I-II = +115,42 +0,04 = +115,46 м.

Исправленные приращения координат записывают в графы 8 и 9 табл. 1.

 

2.1.5. Вычисление координат

 

Вычисление координат начинают с занесения в графы 10 и 11 известных координат начальной точки х_нач, у_нач.

Координаты точек теодолитного хода получают по формулам

x_{i + 1} = x_i + Dx_i ¢;

                                           y_i+1 = y_i + Dy_i¢,                                   (2.15)

где x_i+1 и y_i+1 – координаты последующей точки теодолитного хода;

x_i и y_i – координаты предыдущей точки;

Dx_i¢ и Dу _i¢ – исправленные приращения координат.

В нашем примере

x_II = x_I + Dx ¢_I-II = 6322,70 + 76,64 = 6399,34 м;

y_II = y_I + Dy ¢_I-II = 4057,25 + 115,46 = 4172,71 м.

Вычисленные координаты заносят в графы 10 и 11 табл. 1.

Контролем правильности вычисления координат служит совпадение вычисленных и заданных координат последней точки теодолитного хода (в нашем примере − координаты точки IV).

 

Вычисление высот точек хода и съемочных пикетов

Вычисление высот точек хода

 

Превышения между точками теодолитного хода определяют методом тригонометрического нивелирования по измеренным углам наклона и горизонтальным расстояниям.

Превышения определяют в прямом и обратном направлениях.

 

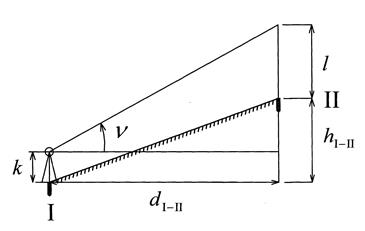
Рис. 7. Тригонометрическое нивелирование

 

Превышение в методе тригонометрического нивелирования определяют по формуле

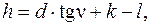                                     (2.16)

где h − превышения между точками хода;

d − горизонтальное расстояние между точками;

n − угол наклона местности;

k − высота прибора;

l − высота визирования (наведения) при измерении вертикального угла.

Обработку результатов тригонометрического нивелирования ведут в журнале (табл. 2) и начинают с вычисления места нуля (МО) вертикального круга теодолита:

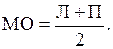                                                                                                   (2.17)

Результаты записывают в графу 7.

В нашем примере для первого угла:

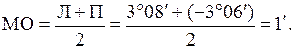
Затем вычисляют углы наклона:

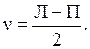                                                                                          (2.18)

Первый угол в нашем примере будет равен

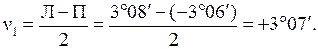
Контроль вычислений может быть сделан по другим формулам:

;

.

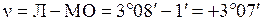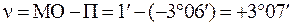Вычисленные углы записывают в графы 8 и 9 табл. 2.

Длины сторон хода (графа 10) выписывают из ведомости вычисления координат (табл. 1, графа 5).

Далее вычисляют значения

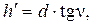                                            (2.19)

Полученные значения 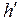 округляют до сантиметров и записывают в графу 11 со знаком, соответствующим знаку угла наклона n.

Превышения h между точками хода получают, учитывая высоту прибора k и высоту визирования l:

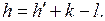                                          (2.20)

Так, для стороны I−II хода имеем:

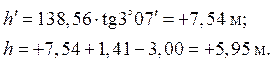
Вычисленное превышение h_I–II выписывают в графу 12 табл. 2.

Превышение для каждой стороны хода получают дважды: превышение h_I–II = +5,94 м называют прямым, а превышение h_II–I = −5,89 м − обратным. Эти превышения имеют разный знак, а по абсолютной величине не должны отличаться больше чем на 4 см на каждые 100 м длины линии. Если указанный допуск соблюдается, то из модулей этих превышений вычисляют среднее арифметическое, и со знаком прямого записывают в графу 13 табл. 2.

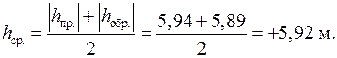
Сумма средних превышений в разомкнутом высотном ходе теоретически должна быть равна разности отметок конечной и начальной точек хода, но вследствие погрешностей в измерении вертикальных углов и длин линий получаем невязку высотного хода:

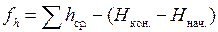                     .                                (2.21)

Величину допустимой невязки в высотных ходах вычисляют по формуле

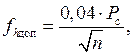                                                                          (2.22)

где Р_с − длина хода в сотнях метров;

n − число сторон хода (количество средних превышений).

Для нашего случая

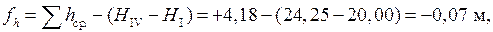
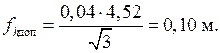
Если полученная невязка не выходит за пределы допустимых значений, то есть 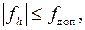то выполняют уравнивание превышений, распределяя полученную невязку пропорционально длинам сторон со знаком, противоположным знаку невязки и вводя во все средние превышения поправки :

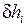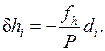                                                                                 (2.23)

Полученные поправки выписывают в графу 14, их сумма должна быть равна невязке и иметь противоположный знак:

.

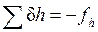Поправками исправляют средние превышения, записывая исправленные превышения в графу 15:

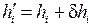.                                         (2.24)

По исправленным превышениям вычисляют высоты точек хода.

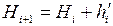                                       .                                      (2.25)

Контролем правильности вычисления отметок служит совпадение вычисленной и заданной отметок конечной точки Н_IV.

 

2.2.2. Обработка журнала тахеометрической съемки

 

Первые графы журнала тахеометрической съемки (табл. 3) содержат результаты полевых измерений.

Обработку журнала начинают с заполнения графы 1, куда из журнала тригонометрического нивелирования (см. табл. 2) переносят для каждой точки теодолитного хода ее отметку (Н _i) и соответствующее место нуля (МО).

Далее вычисляют углы наклона, используя формулу:

                                             n = Л – МО.                                          (2.26)

Например, для точки 1 получим

n = Л – МО = −1°32¢ − 1¢= −1°33¢.

Углы наклона записывают в графу 8 табл. 3.

Затем следует вычислить горизонтальные расстояния d и превышения h. Для этих вычислений используют формулы:

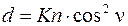;                                           (2.27)

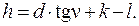                                        (2.28)

В нашем примере:

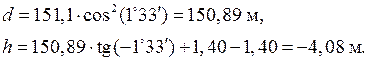
Таблица 2