Все вычисления ведутся в специальной ведомости вычисления координат точек теодолитного хода (табл. 1).

Исходными данными для вычислений являются:

координаты начальной x_нач, у_нач и конечной х_кон, у_кон точек хода (в нашем примере − точки I и IV);

начальный α_нач и конечный α_кон дирекционные углы (в нашем примере − 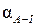 и ).

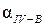Они приведены на первой странице бланка расчетно-графической работы.

Величины измеренных горизонтальных углов и длин сторон теодолитного хода приведены на схеме хода (см. стр. 2 бланка задания).

Уравнивание измеренных горизонтальных углов

Уравнивание углов предусматривает вычисление угловой невязки f_b, сравнение ее с допустимой невязкой f_bдоп и введение поправок 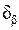 в измеренные горизонтальные углы.

Заполнение ведомости (табл. 1) начинают с графы 1, куда заносят номера вершин хода в порядке их расположения на схеме. В графу 2 со схемы выписывают значения измеренных горизонтальных углов. Там же подсчитывают их сумму ( ).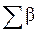

Угловую невязку для разомкнутого хода вычисляют по формуле

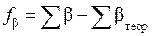,                                  (2.1)

где 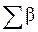 − сумма измеренных углов теодолитного хода;

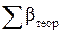   − теоретическое значение суммы горизонтальных углов в ходе.

Для разомкнутого теодолитного хода, в котором измерены правые по ходу углы,

,

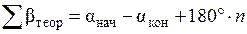где α_нач и α_кон − заданные начальный и конечный дирекционные углы;

n − количество измеренных углов в ходе.

Если , то при вычислении угловой невязки к α_кон прибавляют 360º.

Для нашего примера (табл. 1) имеем:

;

;

.

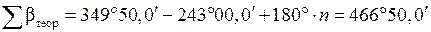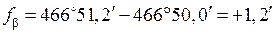Полученную угловую невязку сравнивают с допустимой, вычисляемой по формуле

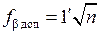.                                           (2.2)

В нашем примере

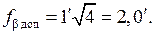
Если угловая невязка окажется больше допустимой, это означает (для расчетно-графической работы), что в вычислениях допущена ошибка, которую надо найти и исправить. Причиной появления угловой невязки в реально проложенных на местности теодолитных ходах являются погрешности в измерении углов.

В нашем случае 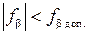, поэтому приступают к уравниванию горизонтальных углов: полученную угловую невязку  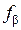распределяют поровну в виде поправок во все измеренные горизонтальные углы со знаком, противоположным знаку невязки.

Поправку в измеренный угол определяют по формуле

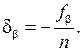                                                                                               (2.3)

Для нашего примера

.

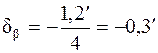Невязка редко делится на число углов без остатка. Поэтому поправки округляют, вводя бóльшие в углы с более короткими сторонами. При этом сумма поправок должна равняться невязке с обратным знаком:

.

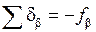Далее вычисляют исправленные углы .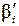

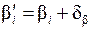.                                        (2.4)

Выписывают их в графу 3 табл. 1 и приступают к вычислению дирекционных углов.