Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

М_Ф= М_{е max} ·β=897·2= 1794 Н·м (1.1)

  где М_{е max} - максимальный момент двигателя, Н·м (М_{е max} = 897 Н*м)

β - коэффициент запаса муфты сцепления(β = 2)

К началу первой строки привязана рамка, полностью строчку не удалать!

Наружный радиус фрикционных накладок можно определить по формуле для автомобилей

 =                                                         

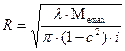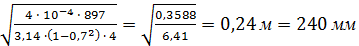
где λ – площадь фрикционной накладки, необходимая для передачи момента в 1 Н·м(λ = 4*10^-4 Н*м)

i– число пар поверхностей трения(i =4);

с – безразмерная величина, выбирается в пределах 0,5-0,7.

 

 

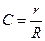 => r = C * R =0,7 * 240 =168 мм

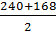=  =204 мм                                                                             

Расчет муфты сцепления на износ

Работа буксования для автомобилей может быть определена по формуле:

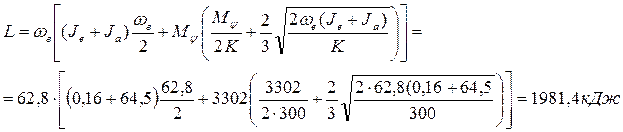
К началу первой строчки привязана рамка, полностью строчку не удалать!

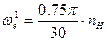= 62,8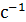                                                                              

где n _Н – номинальная частота вращения вала двигателя.

Величина момента сопротивления дороги M_ψ(Н·м), приведенного к валу муфты сцепления, определяется по формуле

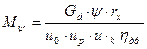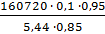= = 3302                        

где G _а - вес автомобиля(160720 Н);

r _к  - радиус колеса, м(0,95 м);

u_ou_pu_к  - передаточные числа главной передачи, раздаточной коробки и коробки передач;( u_к =2,43; 1,44; 0,98;u ₀=5,44; u_p =0)

Ψ= fcosα ± sinα- коэффициент суммарного сопротивления дороги следует брать его среднее значение (0,1).

η _mp - КПД трансмиссии.(0,85)

Момент инерции вращающихся масс двигателя J _е и приведенный к валу муфты сцепления момент инерции автомобиля J _а:

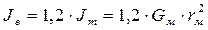= 1,2 · 11 · 0,228²  = 0,16 кг·м²                                        

 =   

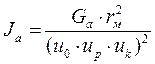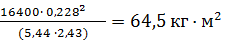
где 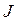_м - момент инерции маховика, кг·м² ;

G _м - масса маховика, кг(11 кг);

r _м- радиус маховика, м(0,22 м);

G _а - масса автомобиля, кг(16400 кг);

r _к - радиус колеса, м(0,491 м);

u_к- передаточное число коробки на первой передаче

 

Проверка муфты сцепления на нагрев

с _g = 481 -удельная теплоемкость нагреваемых деталей муфты (сталь, чугун), Дж/(кг град);

m_g - масса нагреваемой детали, кг.

Значение коэффициента α находят по формуле

=                                                                           

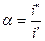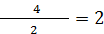
где i’ общее число поверхности трения;

i "- число поверхностей трения у нагреваемой детали.

К началу первой строчки привязана рамка, полностью строчку не удалать!

 

К началу первой строчки привязана рамка, полностью строчку не удалать!

КОНСТРУКТИВНАЯ РАЗРАБОТКА КОРОБКИ ПЕРЕМЕНЫ ПЕРЕДАЧ ЛИАЗ 5256

 

Расчет зубьев

3.1.1 Расчѐт зубчатой пары постоянного зацепления

Исходные данные:

 

Передаточные числа	КПП КамАЗ-141
первая передача	5,62
вторая передача	2,89
третья передача	1,64

 

четвертая передача	1,00
пятая передача	0,724
задний ход	5,30
главная передача	5,44

К началу первой строчки привязана рамка, полностью строчку не удал

ать!

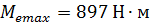 - макс. крутящий момент,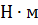

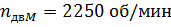 - частота вращения двигателя при макс. моменте

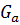= 16400 кг = 160884 Н – вес автомобиля

r _к  =0,95 м - радиус колеса

параметры зубчатой пары: модуль m = 4,5 , число зубьев z₁= 25 , число зубьев z₂= 38 , средний делительный диаметр шестерни первичного вала    d1 = 156,1 мм, делительный диаметр колеса на промежуточном валу          d2 = 171мм, угол наклона зубьев β = 22 град ширина венца b_w1 = 42 мм, b_w2 = 41 мм. Относительная продолжительность работы на передаче αHI=0,01; αHII=0,03; αH3=0,14; αH4=0,82 степень точности по нормам плавности работы n_ст.т = 6, материал – сталь 18Х2НЧВА твердость поверхностей зубьев шестерни HRC 58-63 .

3.1.2 Расчѐт на контактную выносливость активных поверхностей зубьев

 

1.Определяем расчѐтный крутящий момент на промежуточном валу:

 

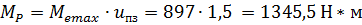
2. Находим расчѐтную окружную силу Рt₁:

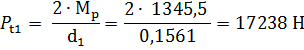
где d₁ – средний делительный диаметр шестерни, м.

 

3. Вычисляем расчѐтную частоту вращения вала:

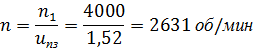
где n1 - частота вращения первичного вала коробки передач, об/мин.

Принимаем n₁ = n_двМ, где n_двМ - частота вращения двигателя при максимальном моменте, об/мин.

4. Определяем параметр контактного напряжения на 1-й ступени:

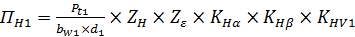
чалу первой строчки  рамка, полностью строчку не удалать!

где Рt1 - окружная сила;

d1 - средний делительный диаметр шестерни, мм;

 ZH - коэффициент контактного напряжения;

Zε - коэффициент, учитывающий степень перекрытия зубчатых колѐс;

 KHα - коэффициент, учитывающий распределение нагрузки между зубьями;

 KHβ - коэффициент, учитывающий распределение нагрузки по ширине венца;

KHV1 - коэффициент, учитывающий динамическую нагрузку в зацеплении.

Коэффициент ZН определяется по следующей зависимости:

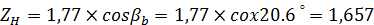
где βb - угол наклона зуба на основном цилиндре, град:

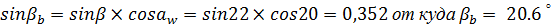
Коэффициент Zε :

- для цилиндрических передач с косозубыми колѐсами Zε=0,796

Коэффициент K_Hα:

- для прямозубых и косозубых цилиндрических передач K_Hα = 1,04 .

Коэффициент K_Hβ:

- для прямозубых и косозубых цилиндрических передач K_Hβ = 1,12

Коэффициент K_HV1:

-для цилиндрических передач K_HV1= 1,04

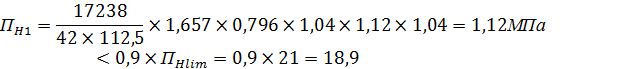
Следовательно, контактная усталость зубчатых колес обеспечена.

5. Определяем предельный параметр контактной выносливости при базовом числе циклов:

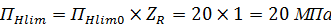
где П_Нlim0 – предел контактной выносливости при стендовых испытаниях колес с заданными размерами, термообработкой и шероховатостью поверхности зубьев, соответствующий базовому числу циклов N_HO = 1,2∙108 МПа;

Z_R – коэффициент, учитывающий шероховатость активной поверхности зубьев более грубого зубчатого колеса в зацеплении, Z_R=1 – класс шероховатости 6.

6. Вычисляем меру накапливаемой усталости за 1 км пробега автомобиля для шестерни и колеса:

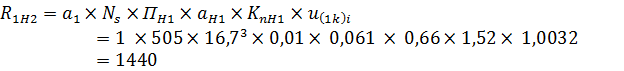
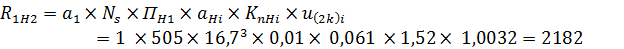
К началу первой строчки привязана рамка, полностью строчку не удалать!

 

где u(_1k)i ,u_(2k)i – передаточные числа соответственно от шестерни и колеса до ведущих колес на i-ой передаче; m_H – показатель кривой контактной усталости; a₁, a₂ – числа циклов, соответствующие одному обороту соответственно шестерни и колеса: для зубчатых колес с одним зацеплением а=1; α_Hi – относительная продолжительность работы на передаче; N_S – суммарное число оборотов ведущего колеса автомобиля за 1 км пробега:

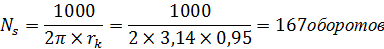
K_nHi – коэффициент пробега на i-й передаче.

Удельная тяговая сила на ведущих колесах:

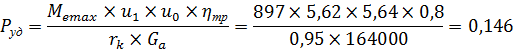
откуда K_nH1 = 0,25

7. Вычисляем расчетное контактное напряжение:

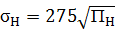=275 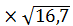= 1123,8 МПа

где П_Н – наибольшее значение параметра при работе зубчатой пары на нескольких ступенях, МПа.

8. Определяем эквивалентное число циклов изменения напряжений:

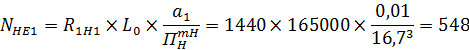
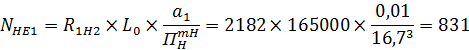
где L_o – планируемый пробег до капитального ремонта (L_o = 165000 км).

9. Находим коэффициент долговечности:

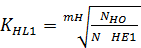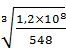=  =60

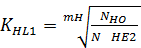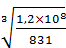=  =52

10. Вычисляем допускаемые контактные напряжения:

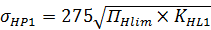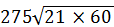= =9761> 0,8σ_lim = 0,8∙3800 =3040 МПа

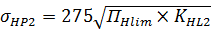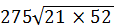= =9081> 0,8σ_lim = 0,8∙3800 =3040 МПа

Принимаем σ_HP1 = σ_HP2 = 3040

11. Проверка условий контактной выносливости:

σ_н < σ_нр      

σ_н = 1182 МПа < 3040 МПа = σ_нр. К началу первой строчки привязана рамка, полностью строчку не удалать!

 

Вывод: условие выносливости по контактным напряжениям выполнено.

 

3.1.3  Расчѐт зубьев колес на выносливость при изгибе

Проверочный расчет выполняют для предотвращения усталостного излома зубьев.

Условие выносливости при изгибе:

 σ_F ≤ σ_FP

где σ_F , σ_FP – соответственно расчетное и допускаемое напряжения изгиба, МПа.

 1. Вычисляем расчѐтные напряжения изгиба зубьев шестерни и колеса:

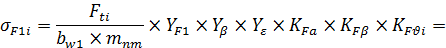
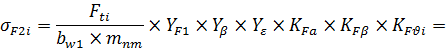
где F_ti - окружная сила, Н;

m_nm - средний нормальный модуль, мм: для цилиндрической передачи m_nm = m_n;

Y_F - коэффициент формы зуба, зависящий от коэффициента смещения и действительного либо эквивалентного числа зубьев (для шестерни – 4, колеса – 3,65);

 Коэффициент Y_β: для прямозубых колѐс Y_β =1, для колѐс с косыми и круговыми зубьями:

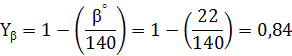
Коэффициент Y_ε: для цилиндрических косозубых и конических передач Y_ε = Z_ε = 0,796.

Коэффициент K_Fα: для прямозубых цилиндрических и конических передач и степени точности n_ст.т= 6, для передач с косыми и круговыми зубьями:

K_Fα =[4+(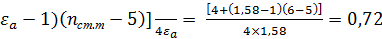

Коэффициент K_Fβ: для цилиндрических передач K_Fβ = 1,12. Коэффициент K_Fv: для цилиндрических передач K_Fv1 = 1,07, K_Fv2 = 1,05

 

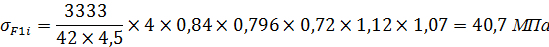
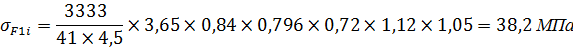
2. Определяем предельное напряжение изгиба при базовом числе циклов:

σ_F1im = σ_с F_1im∙YR∙K_Fc = 460∙1∙1,3 = 546 МПа

где σ_F1im - предел выносливости при базовом числе циклов N_FO и симметричном изгибе зубьев колѐс с заданными конкретными размерами, термообработкой и шероховатостью поверхности зубьев, МПа;

 YR - коэффициент, учитывающий особенности обработки зубьев: YR=1 для цементированных, цианированных, закалѐнных ТВЧ по контуру и улучшению зубчатых колѐс;

 K_Fc – коэффициент, учитывающий отличие характера нагружения зубчатого колеса от симметричного, K_Fc = 1,3 – для одностороннего от нулевого или достаточно близкого к ней цикла (зубчатые колеса низших передач и заднего хода в коробках передач).

Определяем меру накапливаемой усталости за 1км пробега автомобилем по напряжению изгиба:

!

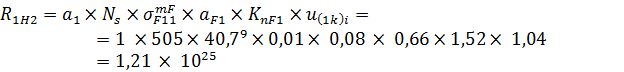
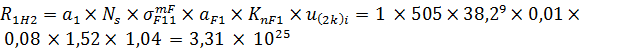
где mF – показатель кривой усталости при изгибе зубьев (mF = 9).

4. Вычисляем эквивалентное число циклов изменения напряжений:

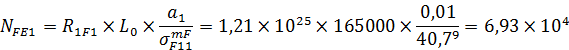
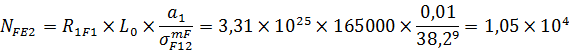
5. Находим коэффициенты долговечности:

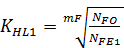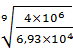=  =1,16

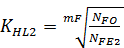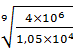=  =1,24

При K_FL < 0,9 принимают K_FL = 0,9.

6. Определяем допускаемые напряжения изгиба:

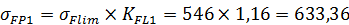
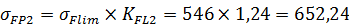
7. Проверка условий прочности по напряжениям изгиба:

σ_F ≤ σ_FP

;

;

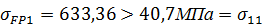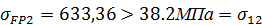Вывод: условие прочности по напряжениям изгиба выполнено. К началу

3.1.4 Расчѐт на прочность

Расчѐт на прочность выполняют с целью предотвращения остаточной деформации или излома зубьев.

Расчѐт выполняют по максимальному динамическому крутящему моменту.

  1.Вычисляем окружную силу:

F_tmax = F_t1∙KД = 17238∙2.2 = 37923,6 Н

где KД – коэффициент динамичности, для легкового автомобиля (KД = 2…3,0 для грузовых автомобилей). Принимаем KД = 2.2.

2. Определяем максимальное контактное напряжение:

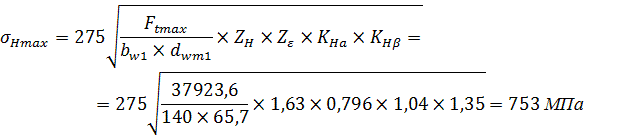
3. Находим максимальные напряжения изгиба зубьев шестерни и колеса:

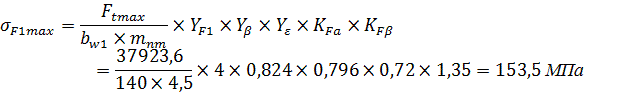
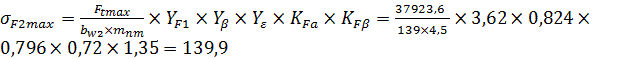МПа

4. Проверка условий достаточной прочности:

σ_Hmax ≤ 0,9σ_HlimM

σ_F1max ≤ 0,9σ_FlimM

σ_F2max ≤ 0,9σ_FlimM

σ_Hmax = 753 МПа < 0,9∙3800 = 3420 МПа

σ_F1max = 153,5 МПа < 0,9∙1700 = 1530 МПа

σ_F2max = 139,9 МПа < 1530 МПа

началу первой строчки привязана рамка, полностью строчку не удалать!

Расчет валов

Валы рассчитывают на статическую прочность, жёсткость и на усталостную прочность для определения их работоспособности и агрегата трансмиссии в целом.