Специальность 12.04.01 «Приборостроение»
« Измерительные информационные технологии»
Перечень основной и дополнительной литературы
Метрология, стандартизация и сертификация : учебник/ [ В.В. Алексеев
-М. Академия, 2014.-368 с.
Шишмарев В.Ю. Технические измерения и приборы: учебник Ь. Академия, 20010.-383 с.
Практикум по вероятностным методам в измерительной технике: учебное пособие для вузов / В.В. Алексеев[ и др.]-СПб : Энергоатомиздат, 1993. –264 с.
В.И. Мудров, В.Л Кушко Методы обработки измерений-М. Советское радио, 1976.-192с.
В.В. Федоров. Теория оптимального эксперимента. М. Наука, 1971, 312 стр.
Программа курса
Раздел 1. Введение в методологию проведения научного эксперимента
Виды научных экспериментов: лабораторный, качественный и количественный эксперименты.
Моделирование физических процессов: масштабное, аналоговое, полунатурное, цифровое моделирование.
Раздел 2. Измерения при проведении научного эксперимента и погрешности результатов.
Прямые и косвенные измерения. Погрешности средств измерений.
Обработка результатов прямых и косвенных измерений
Раздел 3 Элементы теории вероятностей и математической статистики при обработке результатов эксперимента.
Представление экспериментальных данных эмпирическими формулами.
Стационарные и нестационарные случайные процессы.
Экспериментальное определение вероятностных характеристик стационарных случайных процессов.
Экспериментальное определение вероятностных характеристик нестационарных случайных процессов.
Раздел 1. Введение в методологию проведения научного эксперимента
Основные понятия и определения
Научное исследование – изучение различными научными методами того или иного явления или процесса.
Цель научного исследования – получение еще неизвестных знаний о явлении или процессе и дальнейшее полезное использование этих знаний в практической деятельности
Метод исследования представляет собой путь исследования, способ достижения цели, способ решения задачи, при этом к методам эмпирического исследования относят наблюдение, эксперимент, сравнение, описание, измерение.
Основные этапы математического моделирования
1) Построение модели. Выбор типа математической модели. На этом этапе задается некоторый «нематематический» объект — явление природы, конструкция, экономический план, производственный процесс и т. д. При этом, как правило, четкое описание ситуации затруднено. Сначала выявляются основные особенности явления и связи между ними на качественном уровне. Затем найденные качественные зависимости формулируются на языке математики, то есть строится математическая модель. Это самая трудная стадия моделирования.
2) Решение математической задачи, к которой приводит модель. На этом этапе большое внимание уделяется разработке алгоритмов и численных методов решения задачи на ЭВМ, при помощи которых результат может быть найден с необходимой точностью и за допустимое время.
3) Интерпретация полученных следствий из математической модели. Следствия, выведенные из модели на языке математики, интерпретируются на языке, принятом в данной области.
4) Проверка адекватности модели. На этом этапе выясняется, согласуются ли результаты эксперимента с теоретическими следствиями из модели в пределах определенной точности.
5) Модификация модели. На этом этапе происходит либо усложнение модели, чтобы она была более адекватной действительности, либо ее упрощение ради достижения практически приемлемого решения.
Имитационное моделирование.
Имитационное моделирование есть процесс конструирования на ЭВМ моделей, сложной реальной системы.
Выделим ряд обстоятельств учитывающих особенности применения названного метода для исследования системы:
1. имитационное моделирование включает два этапа:
1.1. Конструирование модели на ЭВМ;
1.2. Проведение экспериментов с этой моделью.
2. В соответствии с принципами должны быть выделены две возможные цели имитационных экспериментов:
2.1 понять поведение исследуемых систем;
2.2 Оценить или определить возможные стратегии управления системой.
3. С помощью имитационного моделирования исследуют сложные системы.
4. Метод имитационного моделирования исследует системы, функционирующие во времени. Это определяет необходимость создания и использования специальных методов управления системным временем.
Планирование эксперимента
По характеру получения экспериментальных данных, методика планирования эксперимента подразделяется на пассивный и активный эксперименты.
Пассивный эксперимент (ПЭ) предусматривает измерение только выбранных показателей (параметров, переменных) в результате наблюдения за объектом без искусственного вмешательства в его функционирование. Информация об исследуемом объекте накапливается путем пассивного наблюдения, то есть информацию получают в условиях обычного функционирования объекта. В пассивном эксперименте исследователь не может вмешиваться в процесс ведения эксперимента.
Пассивный эксперимент служит для уточнения и формализации гипотезы, построения теории: В рамках пассивного эксперимента проводится:
ü конструирование шкал, методов, техники измерения, сбор данных для проверки заранее сформулированных гипотез;
ü анализ применения шкал, методов, техники измерения, определение возможных направлений исследования собранной информации, эмпирическое описание поведения объекта
Пассивный эксперимент имеет следующие недостатки:
ü диапазон изменений факторов незначителен и не превышает значений, ограничиваемых инструкцией;
ü влияние возмущающих параметров может оказаться более существенным, чем изменение контролируемых факторов.
Недостатки снижают надежность результатов. Но, несмотря на них, пассивный эксперимент широко применяется для глубокого анализа результатов работы процессов и аппаратов. Примером пассивного эксперимента может быть анализ работы схемы, которая не имеет входов, только выходы, и повлиять на ее работу невозможно.
Активный эксперимент (АЭ) проводится с применением искусственного воздействия на объект по специальной программе. При активном эксперименте изменение параметров проводится в более широких пределах, нежели при выполнении пассивного эксперимента. По специальной программе выполняется однофакторный эксперимент (поочередное варьирование интересующих факторов) – например, варьирование одного фактора при стабилизации других (метод Гаусса-Зайделя); многофакторный (варьируются все переменные и каждый эффект оценивается по результатам всех опытов, проведенных в данной серии экспериментов) – одновременное изменение нескольких факторов (градиентные методы и т.д.). Более надежные результаты получаются при обработке данных активного эксперимента.. Активный эксперимент позволяет получить более точную информацию о процессе.
Активный эксперимент предполагает возможность воздействия на ход процесса и выбора уровней факторов. При планировании АЭ решается задача выбора факторов, влияющих на объект и определение числа проводимых опытов. Увеличение числа факторов приводит к возрастанию числа опытов, а уменьшение – к увеличении погрешности опыта. Фактор задан в том случае, если указала область определения – значения, которые принимает данный фактор. При активном эксперименте факторы должны быть управляемы, независимы и должна быть указана точность измерения факторов в выбранном диапазоне.
Фактически, эксперимент всегда представляет собой нечто среднее, сочетающее в себе черты и свойства активного и пассивного экспериментов.
Основные концепции математического эксперимента, обеспечивающие реализацию задач исследования. Структурная схема эксперимента.
Математическая теория эксперимента определяет условия оптимального проведения исследования. Для этого используются математические методы при подготовке и проведении опытов. Это позволяет исследовать и оптимизировать сложные системы и процессы, обеспечить высокую точность и эффективность эксперимента.
После каждой небольшой серии опытов производится обработка результатов, наблюдений и принимается основное решение о том, что делать дальше.
При исполнении методов математического планирования возможно:
1. Решать различные задачи, связанные с изучением сложных процессов и явлений;
2. Проводить эксперименты с целью адаптации технологического процесса, выявление оптимальных условий его протекания и, таким образом, обеспечить высокую эффективность этого процесса.
Теория математического эксперимента содержит ряд концепций:
1. Концепция рандомизации;
2. Концепция последовательного эксперимента;
3. Концепция математического моделирования;
4. Концепции исполнения факторного пространства.
Принцип рандомизации заключается в том, что в план эксперимента водят элемент случайности. Для этого план эксперимента составляется таким образом, чтобы те систематические факторы, которые трудно поддаются контролю, учитывались статистически и затем исключались в исследованиях как систематические ошибки.
При последовательном проведении эксперимента весь эксперимент выполняется не одновременно, а поэтапно, для того, чтобы результаты каждого этапа анализировать и принимать решение о целесообразности проведения исследований. В результате эксперимента получают уравнение регрессии, которое часто называют моделью процесса.
Важное место в теории планирования эксперимента занимают задачи (вопросы) оптимизации исследуемых процессов, свойств многокомпонентных систем.
Как правило, нельзя найти такое сочетание значений влияющих факторов, при котором одновременно достигается экстремум всех функций отклика. Поэтому в большинстве случаев за критерий оптимальности выбирают лишь одну из переменных состояния функцию отклика, характеризующую процесс, а остальные принимают приемлемыми для данного случая.
Методы планирования эксперимента в настоящее время быстро развиваются, чему способствует возможность широкого использования ЭВМ.
Планирование эксперимента
При современном уравне развития науки и техники многие исследования требуют постановки сложных и дорогостоящих экспериментов. До последнего времени выбор самого эксперимента, где , как и когда его проводить определялся в основном интуицией экпериментатора. Однако с учетом возросшей стоимости проведения эксперимента актуальной становится проблема извлечения наибольшего количества информации с наименьшими затратами. В этой связи становится необходимым применение методов, которые давали бы не только способ обработки экспериментальных данных, но позволяли бы оптимальным образом организовывать эксперимент. Математический аппарат оптимального планирования эксперимента базируется на применении методов математической статистики и методов решения экстремальных задач. Методы математической статистики используются для обоснования разумного выбора критерия оптимальности, после чего проблема оптимальной задачи планирования эксперимента решается как некоторая экстремальная задача.
К настоящему времени можно выделить два основных направления в планировании экспериментов: планирование экстремальных экспериментов и планирование экспериментов по выявлению сути явлений.
В рамках первого направления исследуются условия, при которых процесс удовлетворяет некоторому критерию оптимальности. В рамках второго направления исследуется взаимосвязь между различными параметрами т.е фактически решается задача идентификации модели объекта при различной априорной информации. Предоставив в результате исследований некоторую математическую зависимость между параметрами, мы даем исследователю возможность обобщить полученные результаты в части выявления взаимосвязи явлений.
Рассмотрим подробнее математическую постановку проблемы планирования эксперимента по выявлению механизма явления. Обычно измеряемая величина зависит от ряда параметров , которые будем называть контролируемыми величинами, которые можно представить в виде вектора столбца
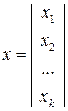
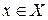, где 
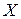-факторное пространство.
Определение области возможных значений контролируемых величин играет важную роль при планировании экспериментов. Задачей эксперимента по поиску математической модели является отыскание связи между измеряемыми величинами и контролируемыми переменными. Эту свазь можно записать в виде
,
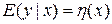где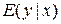 
-условное математическое ожидание при значении 
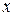контролируемых переменных. Можно рассмотреть три постановки задачи в зависимости от априорной информации
1. Вид функции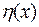 
известен. Требуется определить или уточнить неизвестные параметры
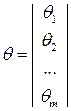
2. Известно, что 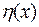совпадает с одной из функций
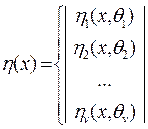
Требуется определить, какая из функций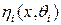 
является истиной и найти неизвестные параметры.
3. Вид функции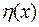 
неизвестен. Известно лишь, что в интересующей области она может быть достаточно хорошо аппроксимирована конечным рядом по некоторой системе наперед заданных функций Требуется найти наилучшее описание функции .
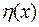Оптимизация в исследовании - (от лат. optimus-наилучший) Под оптимизацией- понимают целенаправленную деятельность, заключающуюся в получении наилучших результатов при соответствующих условиях. Постановка задачи оптимизации предполагает наличие объекта, набора независимых параметров (переменных), описывающих данную задачу, а также условий (часто наз. ограничениями), характеризующих приемлемые значения независимых переменных, которые и образуют модель рассматриваемой системы. Еще одним обязательным условием описания оптимизационной задачи служит мера "качества", носящая название критерия оптимизации и зависящая от переменных . Оптимальное решение оптимизационной задачи - поиск определенного набора значений переменных, которому отвечает минимальное значение критерия оптимальности.
Описанные и построенные модели реального объекта – важнейший этап оптимизационного исследования, так как он определяет практическую ценность получаемого решения и возможность его реализации.
Процесс оптимизации с использованием модели можно рассматривать как метод отыскания оптимального решения для реального объекта без непосредственного экспериментирования с самим объектом. «Прямой» путь, ведущий к оптимальному решению, заменяется «обходным», включающим построение и оптимизацию модели, а также преобразование полученных результатов в практически реализуемую форму. При формировании такой модели следует учитывать характеристики объекта, которые должны быть отражены в модели, а менее существенные особенности в модель можно не включать. Необходимо сформулировать логически обоснованные допущения, выбрать форму представления модели, уровень ее детализации и метод реализации на ЭВМ. Все это относятся к этапу построения модели. Модели можно упорядочить по степени адекватности описания поведения реального объекта. Таким образом, качество модели нельзя оценивать ни по структуре, ни по форме. Единственным критерием такой оценки может служить лишь достоверность полученных на модели примеров поведения реального объекта.
Ошибки классификации
По своему характеру ошибки могут быть отнесены или к систематическим или случайным, однако такое разделение весьма условно.
Выделяют также грубые ошибки, как частный случай случайной ошибки, которые существенно превышают паспортные данные прибора.
Характер образования суммарной ошибки может быть проиллюстрирован следующей схемой
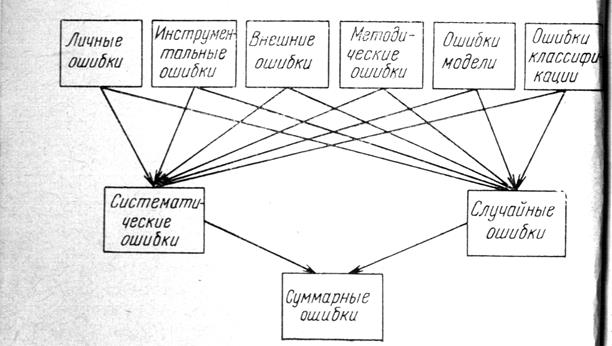
В отношении ошибок, как правило, делаются предположения о характере их статистического распределения. Если такого предположения нет, то параметры законов распределения определяются в рамках общей задачи, либо используется вычислительные методы обработки измерений, например метод наименьших квадратов( МНК).
С учетом ошибок измерений связь между параметрами может быть описана в виде
,
,
………………………
,
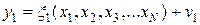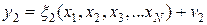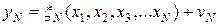которую далее будем называть фундаментальной системой уравнений
Оценки и их классификация
Формально в качестве оценки неизвестного параметра может рассматриваться любая функция измерений 
.
Качество оценки определяется ее свойствами:
несмещенностью, состоятельностью, эффективностью.
Несмещенность
Оценка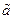 
параметра 
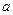называется несмещенной, если выполняется условие
,
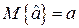Где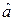 
-оценка случайной величины 
.
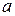Состоятельность
, Оценка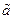 
параметра 
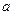называется состоятельной, если с ростом числа опытов 
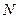она сходится по вероятности к параметру .
.
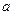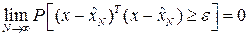Эффективность
Оценка 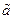параметра 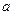называется эффективной, если она обладает минимальной дисперсией, т.е.
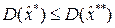
где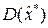 
-ковариационная матрица эффективной оценки, 
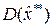-ковариационная матрица любой другой оценки,
Насколько точно можно оценить неизвестные параметры? Неравенство Рао-Крамера.
Неравенство показывает, насколько точно можно оценить неизвестные параметры по ограниченной выборке.
Выведем это неравенство для несмещенной оценки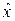 
Для несмещенной оценки имеет место соотношение
где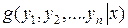 
- условная плотность совместного распределения величин 
.
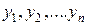Продифференцировав это выражение по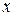 
, получим
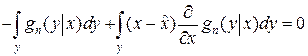
откуда следует, что
.
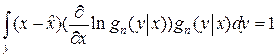Применяя к этому выражению неравенство Коши-Буняковского получим
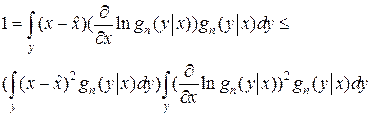
Заметим, что в правой части первый интеграл представляет собой по определению дисперсию
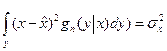
и, как следствие имеем
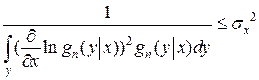
Можно показать, что знак равенства
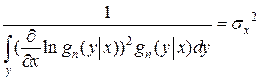
имеет место только в случае, когда
.
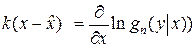Величину, стоящую в знаменателе
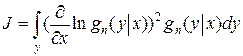
Р. Фишер назвал информацией, содержащейся в выборке.
Если предположить, что измерения независимы и равноточны, имеем
= 
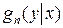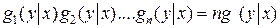и неравенство информации можно записать в виде
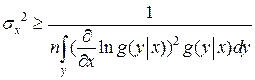
Пример. Пусть производится оценка математического ожидания нормального распределения
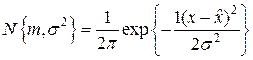
В этом случае
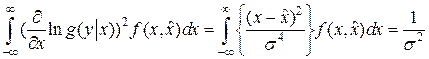
Следовательно, в рассматриваемом примере дисперсия любой регулярной оценки удовлетворяет неравенству
,
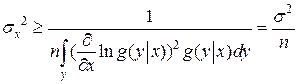но это дисперсия среднего арифметического, распределенного по нормальному закону. Это означает, что среднее арифметическое является эффективной оценкой математического ожидания.
Классификация оценок по методам их получения.
Различают два случая: когда известна плотность распределения случайной величины и когда статистическое описание случайной величины неизвестно. В первом случае получили распространение такие методы как метод наименьших квадратов (МНК) , метод максимального правдоподобия, метод наименьших модулей (МНМ), метод моментов, байесовский метод. В рамках этих методов лежит рассмотрение совместной плотности измерений и оцениваемых параметров, позволяющих в ряде случаев получать оптимальные оценки путем минимизации соответствующих функционалов, зависящих от плотности.
Например, если задать функционал
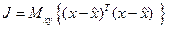
и решитьзадачу минимизации этого функционала, то такая задача обеспечивает получение оценки с минимумом среднего квадрата ошибки вектора состояния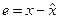 
Ко второму случаю относятся методы, которые не предполагают знания плотности распределения и рассматриваются просто как некоторые удобные вычислительные процедуры получения оценок.
Рассмотрим вначале вычислительные методы, в частности, метод наименьших квадратов. В рамках этого метода функционал, подлежащий минимизации задается в виде
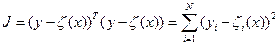
где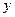 
-вектор ошибок измерений, 
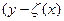-величина называемая невязкой ошибок измерений.
Как следствие, в рамах этой задачи определяется такое значение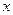 
принимаемое далее за оценку этого вектора, которое минимизирует сумму квадратов невязок.
Метод, в рамках которого достигается получение этой оценки получил название метода наименьших квадратов( МНК).(least square method) (LSM)
Оценку полученную по МНК можно записать в виде
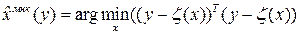
Для того, чтобы определить минимум функционала
Нужно взять частные производные по каждой компоненте вектора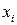 
И получить систему уравнений, получивших название нормальных
(*)
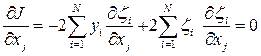Решая такую систему по методу итераций, можно найти требуемую оценку вектора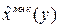 
следует иметь в виду, что решение уравнений (*) могут соответствовать точкам перегиба, а метод итераций сходится к точкам локальных минимумов.
Заметим, что в рамках метода наименьших квадратов рассматривается также критерий , отражающий разную точность получения измерений
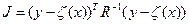
где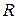 
матрица ошибок измерений Если матрица ошибок измерений диагональна
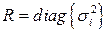
минимизируемый критерий можно представить в виде
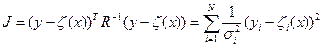
В этом случае говорят об обобщенном методе наименьших квадратов (ОМНК)
В ряде случаев при обработке методом наименьших квадратов используют априорную информацию, для чего фундаментальную систему уравнений
Дополняют уравнениями
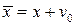
где параметр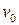 
отражает неточность априорной информеции Если эту неточность охарактеризовать матрицей вторых центральных моментов выражения, используемые в методе наименьших квадратов модефицируются и принимают вид
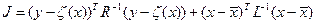
которая при диагональнах матрицах 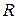и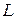 
примут вид
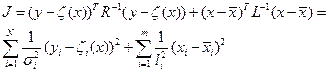
где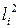 
диагональные элементы матрицы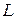
Такой метод наименьших квадратов получил название модифицированного метода наименьших квадратов.
Рассмотрим теперь частный случай фундаментальной системы измерений а именно случай линейных измерений
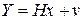
В этом случае
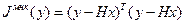
И система нормальных уравнений примет вид
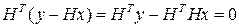
Решая эту систему уравнений, получим выражение для оценки
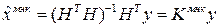
Для получения оценки в рамках ОМНК запишем
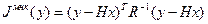
откуда можно получить следующую систему нормальных уравнений
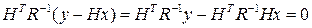
откуда
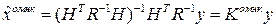
Для получения оценки в рамках ММНК рассмотрим функционал
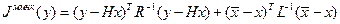
Проводя несложные преобразования, можно получить следующее выражение для оценки
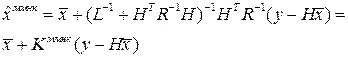
Решение линейной задачи
Будем полагать, что известна совместная плотность распределения с матрицей вторых центральных моментов
,
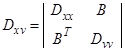а измерения линейны
.
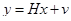В этом случае можем записать для вектора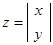 
выражение для ковариационной матрицы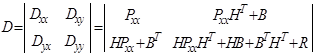 
Если ошибки не коррелированны, т.е.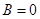 
имеем
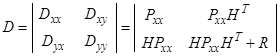и, как следствие формулы оптимального линейного фильтра принимают вид
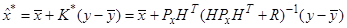
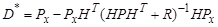
Решение нелинейной задачи
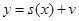
Рассмотрим решение нелинейной задачи, полагая, что известна совместная плотность распределения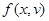 
Для использования линейного оптимального алгоритма необходимо знание следующих параметров:,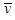 
, 
, 
.
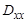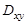
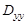Эти параметры могут быть определены следующим образом
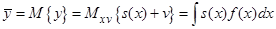
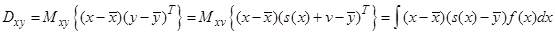
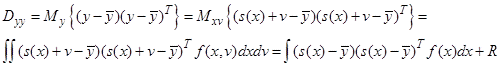
Отметим, что кроме знания моментов требуется также знание плотности распределения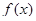 
Пример
, 
, 
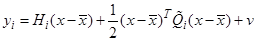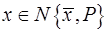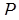-диагональная матрица
Введем обозначения
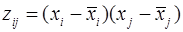. Вектор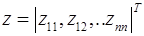 
Тогда
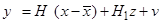
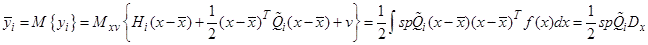
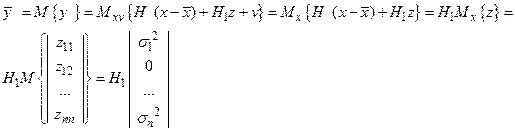
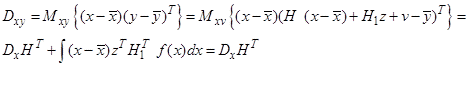
Здесь учтено, что нечетные центральные моменты гауссовской плотности равны нулю.
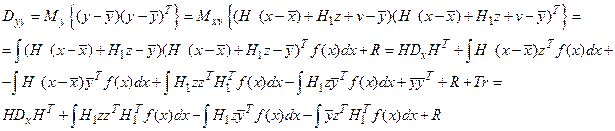
Рассмотрим 
.
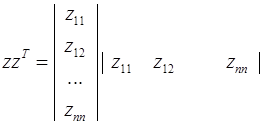Нетрудно заметить, что для случая некоррелированности компонент вектора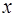 
это произведение будет диагональной матрицей с элементами
.
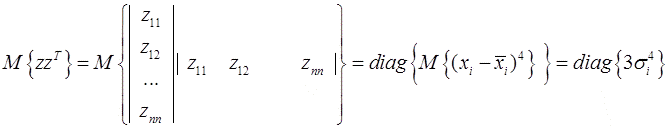Рассмотрим члены
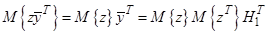
и произведение
.
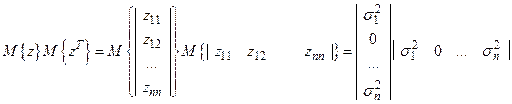Нетрудно заметить что это произведение будет матрицей содержащей ненулевые элементы вида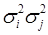 
Байесовский подход. Оптимальные оценки
Выше было показано, что для нахождения оптимальной оценки в рамках байесовского подхода требуется вычисление интеграла
,
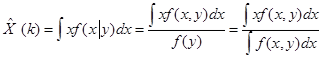при этом средняя действительная ковариационная матрица ошибки оценки определяется выражением
, 
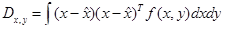
а условная ковариационная матрица выражением
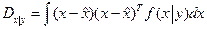
Свойства оптимальных оценок
Свойство 1. Несмещенность оценки
Действительно имеем
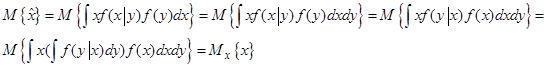
Свойство 2. Ортогональность ошибки оценки
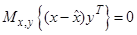
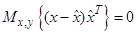
Пусть
, 
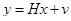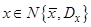
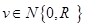
Можно показать, что параметры условной гауссовой плотности распределения для двух совместно гауссовских векторов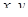 
определяются выражениями
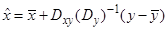
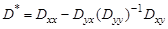
С учетом модели измерений имеем
,, 
,
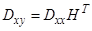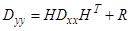Откуда следует
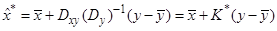
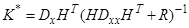
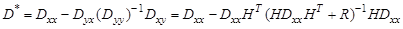
Нетрудно убедиться в том, что в линейной гауссовой задаче оптимальная оценка в среднеквадратическом смысле является эффективной.
Обобщенный фильтр Калмана
Его особенностью является использование в качестве точки линеаризации значения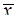 
. В этом случае выражения фильтра примут вид
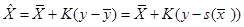
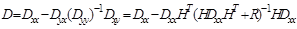
Леммы об обращении матриц
Первая лемма .Имеет место соотношение
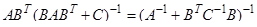
Доказательство
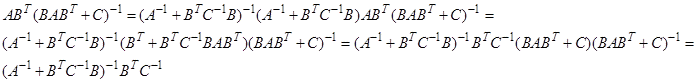
Вторая лемма Имеет место соотношение
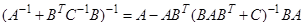
Доказательство
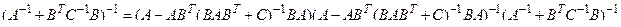
Преобразуя второй сомножитель с помощью первой леммы получаем
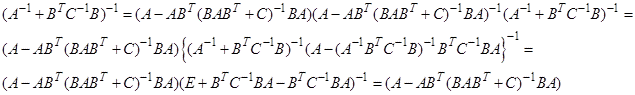
Непрерывный фильтр Калмана
Предположим, что задан непрерывный марковский процесс
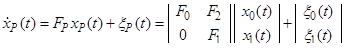
и имеются непрерывные измерения
, 
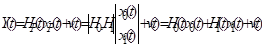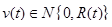
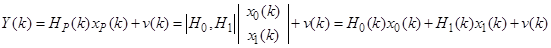
где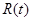 
-интенсивность белошумной ошибки измерений.
В рамках теории линейной фильтрации показано, что оценку с минимальной ковариационной матрицей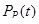 
можно получить с использованием выражений
,
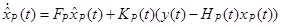
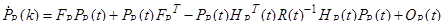получивших название непрерывного фильтра Калмана.
Заметим, что выражение для оценки можно преобразовать к виду
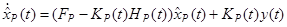
которое можно трактовать как уравнение динамической системы с сигналом на входе системы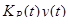 
Для непрерывного фильтра Калмана можно получить дифференциальное уравнение для ошибки оценки
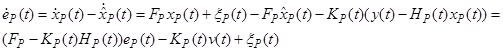
и, как следствие, можно получить следующее выражение для действительной ковариационной матрицы ошибки оценки
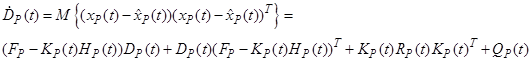
Спектральная плотность
Спектральная плотность определяется как преобразование Фурье от корреляционной функции.
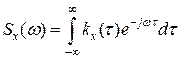
Справедливо и обратное представление
(*)
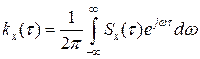В силу четного характера функци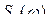й 
и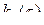 
приведенные соотношения можно записать как
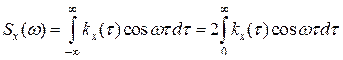
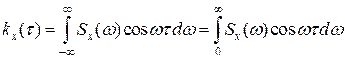
Из выражения (*) вытекает, в частности, соотношение
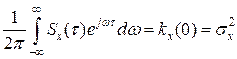
Известно, что корреляционной функции вида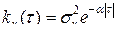 
соответствует спектральная плотность
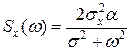
Графики спектральной плотности приведены на рисунке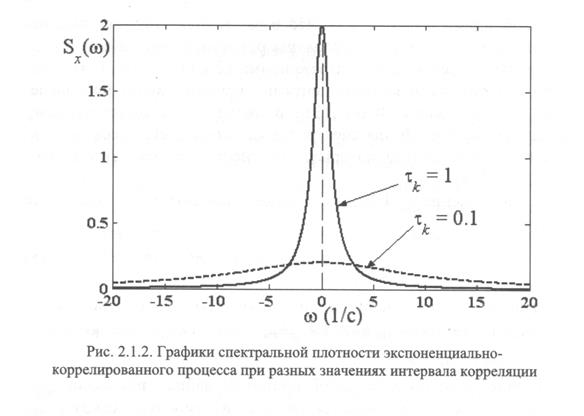 
или в логарифмическом масштабе
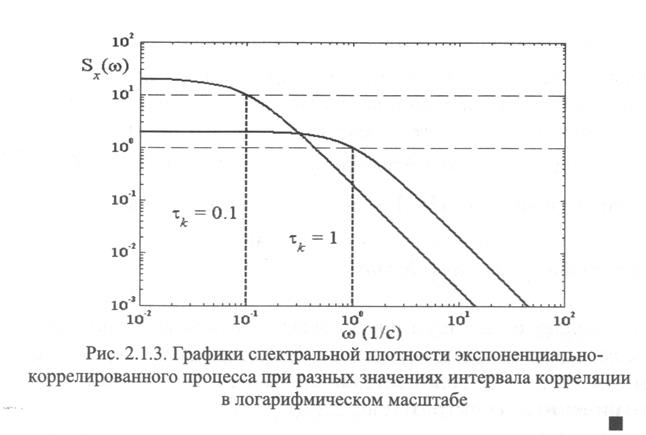
Процесс у которого спектральная плотность отлична от нуля в широком диапазоне частот называется широполосным процессом.
Белый шум
Процесс для которого во всем диапазоне частот спектральная плотность постоянна
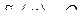
называется белым шумом
Величина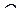 
называется интенсивностью белого шума
Корреляционная функция для белого шума имеет вид
,
с учетом следующего представления для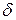 
-функции
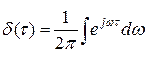
Поскольку белый шум является абстрактным процессом то разумным является введение белого шума с ограниченным спектром
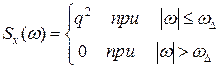
т.е. у которого спектральная плотность постоянна и отлична от нуля в определенной полосе частот (см. рис.)
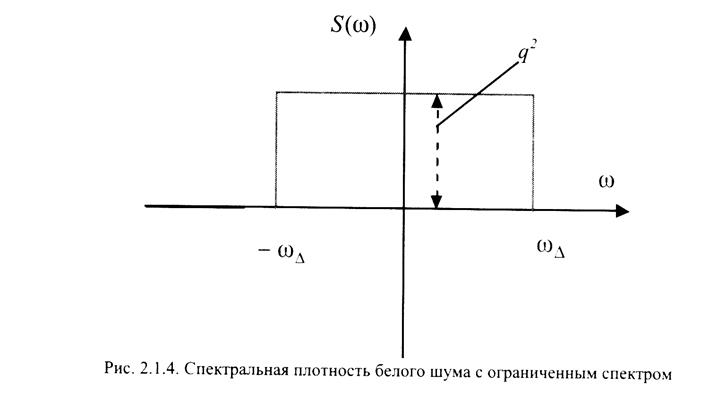
Получим корреляционную функцию такого процесса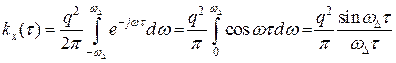 
В частности при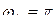 
имеем
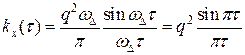
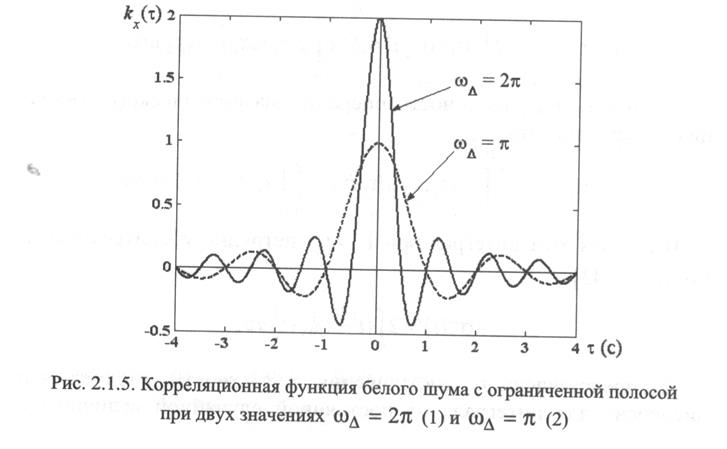
Отметим, что в пределе при увеличении полосы пропускания корреляционная функция стремится к дельта функции.
Метод вариации Аллана.
Иногда оценку дисперсии можно определить как
(*)
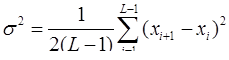Можно показать, что такая оценка будет несмещенной и состоятельной
Предположим теперь, что имеется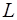 
наборов из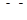 
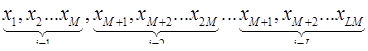
И для каждого из них вычисляется среднее значение
, 
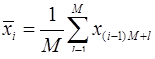Вариация Аллана определяется следующим образом
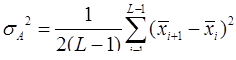
Отсюда следует, что вариация Алана представляет собой оценку одной второй дисперсии разности ( приращений) средних значений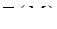 
, рассчитанных для каждой группы.
Легко показать, что при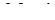 
вариация Аллана совпадает с полученной с помощью выражения (*) оценки дисперсии.
Вводя знак осреднения по ансамблю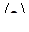 
можем записать
.
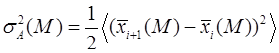Для процесса с непрерывным временем определяем
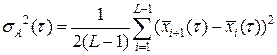
или
,
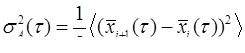где
-
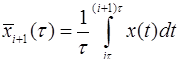среднее на интервале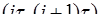 
.
Пример Рассмотрим случайный процесс в виде линейного тренда
. Найдем вариацию Аллана.
Поскольку
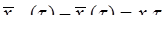, то очевидно, что
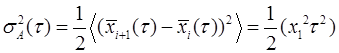
Пример. Найти вариацию Аллана для белого шума интенсивности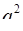 
.
Так как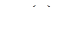 
представляют собой независимые случайные величины с дисперсией 
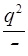, то дисперсия приращений будет равна 
.
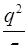Пример. Найти вариацию Аллана для винеровского процесса
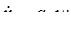
где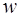 
-белый шум единичной интенсивности
В этом случае дисперсии независимых между собой случайных величин
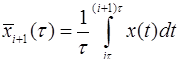определяются как 
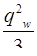. Таким образом 
.
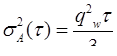В работах по вариациям Аллана вводят еще две составляющие: так называемый фликкер шум для которого вариация Алана постоянна и шум квантования, длят которого вариация алана зависит от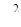 
. Эти процессы можно рассматривать как случайные процессы со спектральными плотностям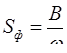и 
и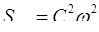 
.
Выражение при наличии всех упомянутых составляющих запишется в виде
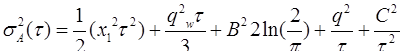
Иногда вариации Аллана изображают в логарифмическом масштабе с типовыми наклонами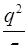
.
Достоинством вариаций Аллана является их использование для нестационарных процессов
Если процессы стационарны можно показать, что имеется соледующая взаимосвязь между вариацией Алана и спектральной плотностью
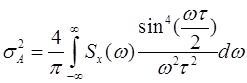
Действительно, можно записать
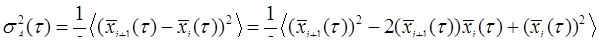
Последнее слагаемое может быть представлено как
где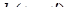 
корреляционная функция исследуемого процесса.
Тогда
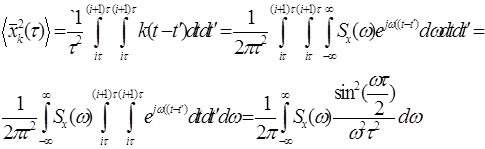
Решение задач сглаживания
Специфика задач сглаживания заключается в выработке оптимальных оценок в момент времени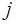 
с использованием всей совокупности полученных к текущему моменту времени измерений.Выделяют три типа задач сглаживания;
-сглаживание на закрепленном интервале;
-сглаживание в фиксированной точке;
-сглаживание с постоянным запаздыванием.
В задаче сглаживания на закрепленном интервале фиксируется общее количество измерений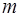 
и отыскиваются оценки для каждого момента времени 
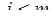с использованием всей совокупности измерений.
В задаче сглаживания в фиксированной точке фиксируется момент времени на которую вырабатывается оценка с использованием всей совокупности измерений.
В задаче сглаживания с постоянным запаздыванием производится выработка оценки на момент времени, отстоящий на фиксированное число шагов от текущего момента времени
Особенности использования информации приведены на рисунке
Решение задачи сглаживания на закрепленном интервале;
Рассмотрим три подхода к решению задачи сглаживания:
-с использованием расширенного пространства состояния;
- с использованием комплексирования оценок, полученных в прямом и обратном времени;
- с использованием уточнения оценок в обратном времени.
Решение задачи сглаживания рассмотрим в постановке когда модель поведения динамической системы и процесса измерений имеет вид
, 
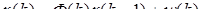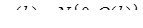
а процесс измерений в дискретные моменты времени описывается моделью с аддитивными ошибками измерений
, 
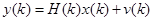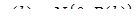
Специальность 12.04.01 «Приборостроение»
« Измерительные информационные технологии»
Дата: 2018-12-28, просмотров: 334.
