Как и все люди, абоненты сети передачи данных могут не доверять друг другу или вести себя нечестно. Они могут подделывать чужие сообщения, отрицать свое авторство или выдавать себя за другое лицо. Особенно актуальными становятся эти проблемы в связи с развитием электронной коммерции и возможностью оплаты услуг через Интернет. Поэтому во многих системах связи получатель корреспонденции должен иметь возможность удостовериться в подлинности документа, а создатель электронного послания должен быть в состоянии доказать свое авторство получателю или третьей стороне. Следовательно, электронные документы должны иметь аналог обычной физической подписи. При этом подпись должна обладать следующими свойствами:

1. подпись воспроизводится только одним лицом, а подлинность ее может быть удостоверена многими;

2. подпись неразрывно связывается с данным сообщением и не может быть перенесена на другой документ;

3. после того, как документ подписан, его невозможно изменить;

4. от поставленной подписи невозможно отказаться, то есть лицо, подписавшее документ, не сможет потом утверждать, что не ставило подпись.

Асимметричные алгоритмы шифрования могут быть использованы для формирования цифровой (электронной) подписи (digital signature) – уникального числового дополнения к передаваемой информации, позволяющего проверить ее авторство. Электронная (цифровая) подпись (ЭЦП) представляет собой последовательность бит фиксированной длины, которая вычисляется определенным образом с помощью содержимого подписываемой информации и секретного ключа.

При формировании цифровой подписи специальным образом шифруется или все сообщение целиком, или результат вычисления хеш-функции от сообщения. Последний способ обычно оказывается предпочтительнее, так как подписываемое сообщение может иметь разный размер, иногда довольно большой, а хеш-код всегда имеет постоянную не очень большую длину. Рассмотрим подробнее оба варианта формирования ЭЦП.

Самый простой способ основывается, так же как и при открытом шифровании, на использовании пары связанных между собой ключей (открытого и закрытого). Однако роли закрытого и открытого ключей меняются – ключ подписывания становится секретным, а ключ проверки – открытым. Если при этом сохраняется свойство, что по открытому ключу нельзя практически найти закрытый ключ, то в качестве подписи может выступать само сообщение, зашифрованное секретным ключом. Таким образом подписать сообщение может только владелец закрытого ключа, но каждый, кто имеет его открытый ключ, может проверить подпись.

Пусть, например, пользователь А хочет отправить пользователю Б подписанное сообщение. Процедура создания и проверки подписи состоит из следующих шагов:

1. Пользователь А посылает пользователю Б свой открытый ключ U по любому каналу связи, например, по электронной почте.

2. Пользователь А шифрует сообщение М своим закрытым ключом R и получает зашифрованное сообщение С.

3. Зашифрованное сообщение пересылается пользователю Б.

4. Пользователь Б расшифровывает полученное сообщение С, используя открытый ключ пользователя А. Если сообщение расшифровалось, значит, оно подписано пользователем А.

Этот протокол можно изобразить в виде схемы, как на рис. 9.2.

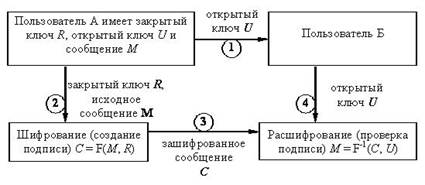
Рис. 9.2. Первый вариант схемы создания и проверки цифровой подписи

До тех пор, пока пользователь А надежно хранит свой закрытый ключ, его подписи достоверны. Кроме того, невозможно изменить сообщение, не имея доступа к закрытому ключу абонента А; тем самым обеспечивается аутентификация и целостность данных.

Физическое представление пары ключей зависит от конкретной системы, поддерживающей использование ЭЦП. Чаще всего ключ записывается в файл, который, в дополнение к самому ключу, может содержать, например, информацию о пользователе - владельце ключа, о сроке действия ключа, а также некий набор данных, необходимых для работы конкретной системы. Данные о владельце ключа позволяют реализовать другую важную функцию ЭЦП - установление авторства, поскольку при проверке подписи сразу же становится ясно, кто подписал то или иное сообщение. Обычно программные продукты, осуществляющие проверку ЭЦП, настраиваются так, чтобы результат исполнения появлялся на экране в удобном для восприятия виде с указанием поставившего подпись пользователя, например, так:

На рис. 9.2 представлена схема формирования так называемой цифровой подписи с восстановлением документа. Цифровые подписи с восстановлением документа как бы содержат в себе подписываемый документ: в процессе проверки подписи автоматически вычисляется и тело документа. Если при расшифровывании сообщение восстановилось правильно, значит, подпись была верной. Цифровая подпись с восстановлением документа может быть реализована, например, с помощью одного из самых популярных алгоритмов формирования ЭЦП –RSA.

В случае использования цифровой подписи с восстановлением документа все сообщение целиком подписывается, то есть шифруется. В настоящее время на практике так обычно не делается. Алгоритмы шифрования с открытым ключом достаточно медленные, кроме того, для подтверждения целостности сообщения требуется много памяти. К тому же практически все применяемые алгоритмы вычисления ЭЦП используют для расчета сообщения заранее заданной стандартной длины. Например, в российском алгоритме формирования цифровой подписи ГОСТ Р34.10-94 этот размер определен равным 32 байтам. Поэтому для экономии времени и вычислительных ресурсов, а также для удобства работы асимметричный алгоритм обычно используется вместе с какой-нибудь однонаправленной хеш-функцией. В этом случае вначале с помощью хеш-функции из сообщения произвольной длины вычисляется хеш-код нужного размера, а затем для вычисления ЭЦП производится шифрование полученного на предыдущем этапе хеш-кода от сообщения.

ЭЦП, вычисленные по хеш-коду документа, называют присоединяемыми цифровыми подписями. Такие цифровые подписи представляют собой некоторый числовой код, который необходимо пристыковывать к подписываемому документу. Само сообщение при этом не шифруется и передается в открытом виде вместе с цифровой подписью отправителя.

Если пользователь А хочет отправить пользователю Б сообщение М, дополненное присоединенной цифровой подписью, то процедура создания и проверки подписи должна состоять из следующих шагов:

1. Пользователь А посылает пользователю Б свой открытый ключ U по любому каналу связи, например, по электронной почте.

2. Пользователь А с помощью некоторой надежной хеш-функции Н вычисляет хеш-код своего сообщения h = H(M).

3. Затем пользователь А шифрует хеш-код сообщения h своим закрытым ключом R и получает цифровую подпись С.

4. Исходное сообщение М вместе с цифровой подписью С пересылаются пользователю Б.

5. Пользователь Б вычисляет хеш-код h полученного сообщения М, а затем проверяет цифровую подпись С, используя открытый ключ пользователя А.

Этот протокол можно изобразить в виде схемы, как на рис. 9.3.

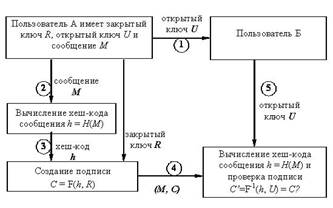
Рис. 9.3. Второй вариант схемы создания и проверки цифровой подписи

Хеш-функция не являются частью алгоритма ЭЦП, поэтому в схеме может быть использована любая надёжная хеш-функция.

Описанный процесс создания подписи не обеспечивает конфиденциальность. То есть сообщение, посланное таким способом, невозможно изменить, но можно прочитать. Даже если не использовать хеш-функцию, а шифровать все сообщение целиком, конфиденциальность не обеспечивается, так как любой может расшифровать сообщение, используя открытый ключ отправителя.

Во многих ситуациях приведенной схемы создания и использования цифровой подписи оказывается вполне достаточно. Однако бывают случаи, когда пользователь Б может смошенничать. Предположим, что пересылаемым документом был чек от пользователя А, например, за оказанные услуги. Пользователь Б удостоверился, что цифровая подпись на нем верная и использовал его для получения денег. Никто не может помешать пользователю Б снять одну или несколько копий с подписанного документа (тем более, если документ электронный) и периодически с небольшим интервалом предъявлять их в банк для получения денег.

Для устранения возможности такого жульничества в цифровые подписи часто включают метки времени. Дата и время подписания документа добавляются к сообщению и подписываются вместе со всем документом. При оплате чека метка времени может быть зафиксирована банком и занесена в базу данных. При попытке повторного предъявления чека банк это обнаружит и примет соответствующие меры.

Разновидностью цифровой подписи является неотрицаемая цифровая подпись. Как и обычная цифровая подпись, неотрицаемая цифровая подпись зависит от подписываемого документа и закрытого ключа автора. В отличие от обычной ЭЦП неотрицаемая подпись не может быть проверена без разрешения подписавшего. Таким образом, получатель корреспонденции не сможет показать подпись (или не сможет доказать правильность подписи) без согласия лица, подписавшего сообщение.

Требования к алгоритмам шифрования с открытым ключом

Рассмотрев основные способы применения алгоритмов шифрования с открытым ключом, изучим требования, которым должен, по мнению основоположников теории шифрования с открытым ключом Диффи и Хеллмана, удовлетворять алгоритм шифрования с открытым ключом. Эти требования следующие:

1. Вычислительно легко создавать пару (открытый ключ, закрытый ключ).

2. Вычислительно легко зашифровать сообщение открытым ключом.

3. Вычислительно легко расшифровать сообщение, используя закрытый ключ.

4. Вычислительно невозможно, зная открытый ключ, определить соответствующий закрытый ключ.

5. Вычислительно невозможно, зная только открытый ключ и зашифрованное сообщение, восстановить исходное сообщение.

Алгоритм RSA

Основные сведения

Алгоритм шифрования с открытым ключом RSA был предложен одним из первых в конце 70-х годов ХХ века. Его название составлено из первых букв фамилий авторов: Р.Райвеста (R.Rivest), А.Шамира (A.Shamir) и Л.Адлемана (L.Adleman). Алгоритм RSA является, наверно, наиболее популярным и широко применяемым асимметричным алгоритмом в криптографических системах.

Алгоритм основан на использовании того факта, что задача разложения большого числа на простые сомножители является трудной. Криптографическая система RSA базируется на следующих двух фактах из теории чисел:

1. задача проверки числа на простоту является сравнительно легкой;

2. задача разложения чисел вида n = pq ( р и q — простые числа); на множители является очень трудной, если мы знаем только n, а р и q — большие числа (это так называемая задача факторизации).

Алгоритм RSA представляет собой блочный алгоритм шифрования, где зашифрованные и незашифрованные данные должны быть представлены в виде целых чисел между 0 и n -1 для некоторого n.