Для исследования напряженно-деформированного состояния сложных пространственных конструкций (например, атомных электростанций) (рис. 8.1) применяют поляризационно-оптический метод (метод фотоупругости) [19]

Суть метода состоит в следующем: модели изготавливаются из оптически-чувствительного материала на основе эпоксидной смолы и МТГФ ангидрида в качестве отвердителя. Геометрический масштаб моделей принимается в пределах (1:400) – (1:500) из условия размещения их в нагрузочных приспособлениях (рис. 8.2).

В испытаниях применяется метод «замораживания» деформаций. Модели под нагрузкой нагреваются до t=130°C, затем медленно охлаждаются до комнатной температуры. При этом в них фиксируется («замораживается») напряженно-деформированное состояние конструкции.

Данным методом можно создать следующие внешние нагрузки: собственный вес сооружения; временные нагрузки на перекрытиях блока локализации аварий; повышение аварийного давления в защитной оболочке реактора; реакцию упругого основания.

Упругое основание моделируется плотной резиной с модулем упругости 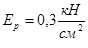. Отношение модулей упругости материала модели и основания примерно равно расчетному для условий упругого сжимаемого слоя конечной глубины при показателе гибкости t=17 [21].

Нагрузки от собственного веса здания, временной нагрузки на перекрытиях блока локализации аварий и реакции упругого основания создается в поле центробежных сил на центрифуге со скоростью вращения 270 оборотов в минуту.

Нагрузка от повышения аварийного давления в защитной оболочке реактора создается нагрузкой обратного знака (вакуумом). При этом изготавливается две модели (для разных видов нагружения). Затем по принципу суперпозиции (независимости действия сил) полученные напряжения в сечениях моделей суммируется.

После остывания модели разрезаются на срезы толщиной (3…4) мм в интересующих сечениях и обрабатываются на поляризационно-оптических установках, которые «считывают» полученные интерференционные полосы (линии равных разностей главных напряжений ( 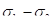))(рис. 8.3, 8.4).

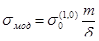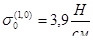Нормальные напряжения на контурах элементов модели конструкции определяют по формуле , где – цена одной интерференционной полосы, полученная по тарировочным испытаниям образцов; 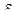– толщина среза из модели; m – порядок полосы.

Для определения напряжений в натурной конструкции используют теорию подобия и размерностей [20].

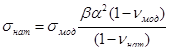
где 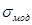– напряжения в модели;

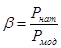– масштаб силового подобия;

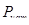– нагрузка в натурной конструкции;

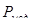– нагрузка, созданная в модели;

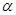– масштаб линейного подобия;

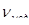; – коэффициент Пуассона, соответственно для материала модели и материала натурного сооружения.

На рис. 8.5, в качестве примера, приведены эпюры нормальных напряжений (в МПа) на гранях элементов блока локализации аварий, полученные при испытаниях моделей при действии собственного веса конструкции, временной нагрузки на перекрытиях и реакции упругого основания.

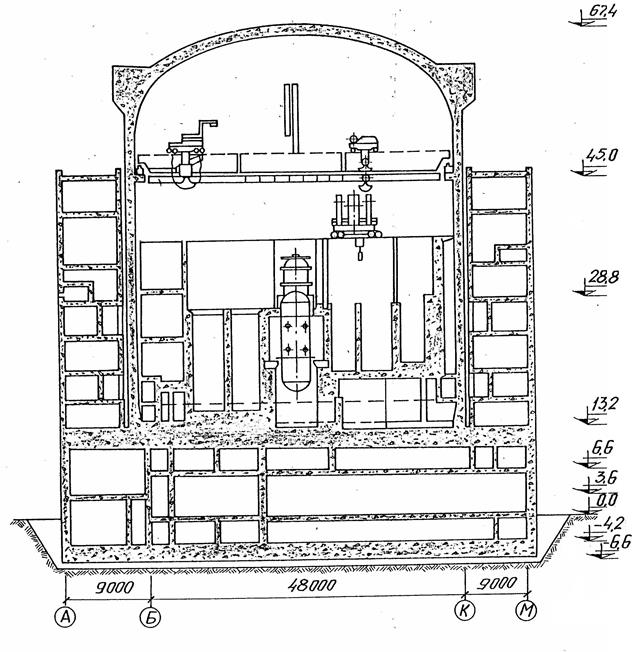
Рис. 8.1 Поперечный разрез по зданию атомной электростанции.

Рис. 8.2 Модель здания атомной электростанции, изготовленная из оптически чувствительного материала.

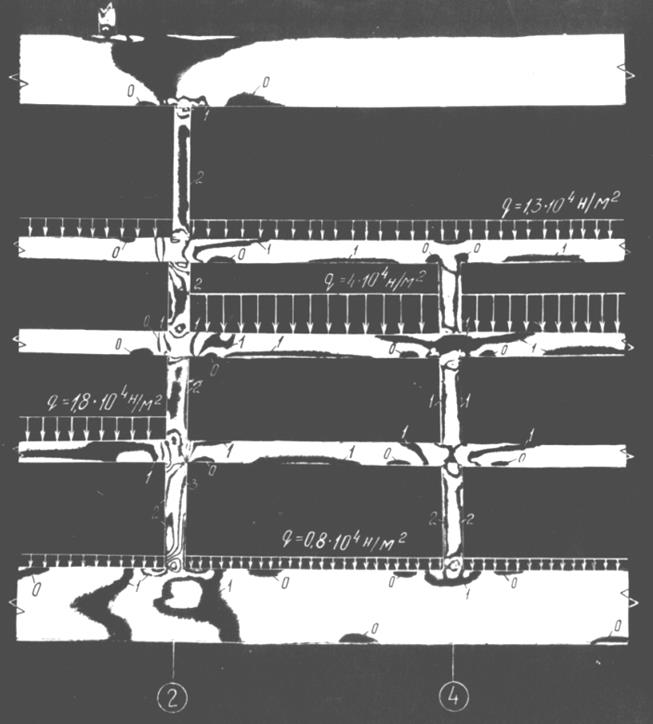
Рис. 8.3 Картина интерференционных полос (линий разности главных напряжений ( ))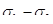

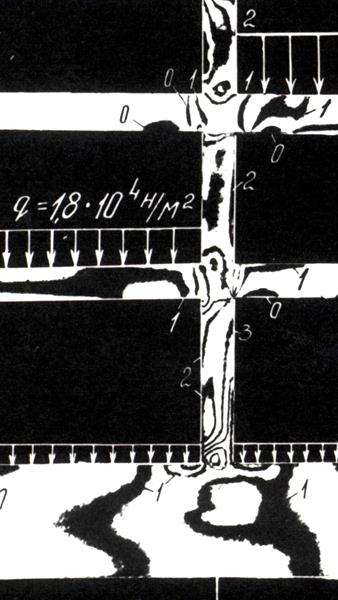
Рис. 8.4 Укрупненный узел картины интерференционных полос (по оси 2). Читать совместно с рис. 8.3.

Рис. 8.5 Эпюры нормальных напряжений (МПа) на контурах элементов блока локализации аварий АЭС

Литература.

1. Корчинский И.Л. Испытание сооружений. Государственное издательство "Высшая школа", М., 1961 г.

2. Аистов Н.Н. "Испытание сооружений" Гос. изд-во литературы по строительству, архитектуре и строительным материалам. Л-М., 1960.

3. Красиков В.И. "Испытание строительных конструкций" Гос. изд-во литературы по строительству и архитектуре. М-Л., 1952.

4. Долидзе Д.Е. "Испытание конструкций и сооружений", Высшая школа, М., 1975.

5. Х. Шенк "Теория инженерного эксперимента", Мир, М., 1972.

6. Новые идеи в планировании эксперимента, под редакцией Налимова В.В., Наука, М., 1969.

7. Алабужев П.М., Геронимус В.Б., Минкевич Л.М., Шековцов Б.А. "Теория подобия и размерностей. Моделирование.", Изд-во Высшая школа, М., 1968.

8. Зайдель А.Н. "Элементарные оценки ошибок измерений", Наука, Л., 1967.

9. Степанов М.Н. "Статистическая обработка результатов механических испытаний", Машиностроение, М., 1972.

10. Бурдук Г.Д., Марков Б.Н. "Основы метрологии", Изд-во стандартов, М., 1975.

11. Маликов С.Ф., Тюрин Н.И. "Введение в метрологию", Изд-во стандартов, М., 1966.

12. К. Финк, Х. Рорбах "Измерение напряжений и деформаций", Машгид, М., 1961.

13. А.Б. Ренский, Д.С. Бараков, Р.А. Макаров "Тензометрирование строительных конструкций и материалов", М., Стройиздат, 1977.

14. Методы неразрушающих испытаний. Физические основы, практические применения, перспективы развития. Под ред. Р. Шарпа, М., Мир, 1972.

Акустическая эмиссия. Ультразвуковая спектроскопия. Ультразвуковая голография. Рентгеновское и гамма излучения. Нейтронная голография.

Методы вихревых токов. Разнотехнические СВЧ-методы. Инфракрасное излучение.

15. Э. Поль "Неразрушающие методы испытаний бетона" Изд-во литературы по строительству, М., 1967.

16. Г.И. Горчаков, Э.Г. Мурадов "Основы стандартизации и контроля качества продукции", Стройиздат, М., 1977.

17. И.С. Лифанов, Н.Г. Шерстюков "Метрология, средства и методы контроля качества в строительстве", Стройиздат, М., 1979.

18. Лужин О.В., Злочевский А.Б. и др. «Обследование и испытание сооружений», М., Стройиздат, 1987.

19. Метод фотоупругости. Под ред. Г.Л.Хесина (в 3-х томах). М., Стройиздат, 1975.

20. Алабужев П.М., Геронимус В.Б. и др. Теория подобия и размерностей. Моделирование., М., Высшая школа, 1968.

21. Завалишин С.И., Смирнов С.Б., Морозова Д.В. Фриштер Л.Ю. Исследование напряженного состояния сферической оболочки АЭС. «Энергетическое строительство». 1994, №4. с.66-67.

22. Доркин В.В., Морозова Д.В., Фриштер Л.Ю. Напряженное состояние защитной оболочки реактора с учетом конструктивных неоднородностей. Проблемы аксиоматики в гидро-газодинамики. Издательство «Век книги», М., 2002., №10, с.173-179.

23. Гучкин И.С. Диагностика повреждений и восстановления эксплуатационных качеств конструкций. Изд-во АСВ, 2001.

24. СП 13-102-2003. Правила обследований несущих строительных конструкций зданий и сооружений. М., 2004.