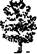Г л a a a 6 ОБЩИЕ СВЕДЕНИЯ О ПРИБОРАХ
С помощью артиллерийских приборов можно:
1) наблюдать, т. е. отыскивать цели, детально их изучать, раз-ведывать поле боя, наблюдать разрывы снарядов;
2) управлять огнём, т. е. определять исходные данные для стрельбы, направлять батарею в цель, рассчитывать перенос, со-средоточеыие огня и т. п.;
3) наводшь оруцие (прнцельные приспособления) ;
4) выполнять топографические работы.
Разрешение болынинства вопросов стрельбы связано с изме-рением углов и расстояний" и с необходимостью наблюдать на большие расстояния.
Поэтому большая часть артиллерийских приборов устроейа так, что они одновременно позволяют* измерять углы и прибли-жают отдаленные предметы, т. е. дают увеличение. Увеличение изображения достигается t помощью системы стёкол (линз). Такие приборы называются оптическіши.
Общне свойства оптических приборов
Основная задача оптических приборов — расйіирить гранацы естественного зрения, йомочь рассмотреть то, чего не в состоянии видеть человеческий глаз.
Приборы эти устроены так, что позволяют наблюдать предме-ты под болыпим углом зрения, чем невооружённым глазом (рис. 113), т. е. как бы приближают их.
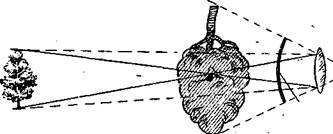
Каждый оптнческий прибор обычно состоиг из нескольких линз (специально обработанных стёкол) и призм (рис. 114). В приборе должно быть не менее двух стёкол: объектива, в ко-торый входят световые лучи от рассматриваемого предмета, и окуляра, с помощью которого рассматривают изображение этого предмета.
Объектив даёт изображение предмета, a окуляр увеличивает угол, под которым предмет виден в приборе.
Призмы, давая полное внутреййее отражение изображения, позволяют изменять направление, по которому идут лучи; благо-
96
|
|
Угоя эрения _ L--------------- — ■
|
|
| Угал зрениа |
Rfic. 113. Угол зрения:
1— при наблюіении простым глазом; 2— при наблюдении в бинокль
даря наличию призм удается расставить объективы бинокля ши-ре окуляров, a c помощью стереотрубы наблюдать, не высовы-ваясь из окопа (см. на рис. 166 ход лучей в стереотрубе).
Большинство артиллерийских приборов позволяет вести на-блюденйе обоими глазами одновременно. Это даёт возможность наблюдателю ощущать, какие предметы находятся дальше, какие ближе (или, как говорят, изображение получается стереоскопич-ным). При наблюдении же одним глазом предметы кажутуся пло-скими, и их взаимное р^асположение почти не различается.
|
|
Чем больше расстояние между объективами, тем' больше стереоско-пичносіь изображения, тем лучше раз-личается его выпуклость и азаимное расположение предметов.*
| Рис. 114. Линзы и призмы: 1 п 2 — лиизы; 3 н 4— призмы |
Поэтому при конструировании ар-тиллерийских приборов обычно стара-ются насколько возможно шире рас-ставить их объеКтивы; тогда приборы повышают естественную стереоскоиич-ность зрения, a это позволяет лучше наблюдать и изучать местность. .
Свойство приборов давать наблюдателю ощушение глубину и рельефности рассматриваемого пространства называется пластич-, ностью прибора. Пластичность прибора выражают числом, пока-зывающим, во сколько4 раз расстояние между объективами боль-ше расстояния между окулярами.
' Оптическиё приборы дают увеличение, благодаря которому наблюдаемые предметы кажутся блнже (больше), чем при на-блюдении невооруженным глазом. Увеличением прибора назы-, вается число, показыв^ющее, no сколько раз угол, под которым виден предмет в прибор, больше угла, под которым тот
Учебник сержанта артиллерии
Q7
же нредмет виден простым глазом. Увеличение обозначается так:
4Х, 6Х, 8Х, 10X, и т. п., и называется четырёхкратѣым, шести-
кратньш, вбсьмиіфатным, десятикратным и' т. п. Эти числа
покаэывают, что видимъге в прибор предметы кажутся наблюдателю
в 4, 6, 8, 10 раз ближе, чем нри наблюдении их невооружённым
глазом. • ' і
У отжееких приборов поле зрения ограничено. Под «полем зревяя» подразумевается часть пространства, которую видит на-блюдатеяь в прибор. В каждый прибор видна лишь небольшая часть простраяства, в несколько раз меньше, чем при наблюдении простым глазом. Велнчина поля зрения тем меныне, чем больше увелячение прибора. Так, например, поле зрения шестикратного би-жжля почтивдвое больше поля зрения десятакратной стереотрубы. '
С&етосилой прибора называется степень освещённоети изо-браження, волучаемого на сетчатже глаза при наблюдешш в прибор. Светосяла зависит от размероа входного и выходного зрачков прибора.
Входмой зрачок — это величина диаметра отверстия объекти-ва; он нзмеряется в миляивдетрах и указывается на приборах. Напршаер, шесгакратный бивокль с диаметром объектива 30 мм имеет обозначение 6X30 (шесть на тридцать). /
Выходным зртком называется »зображение объектива, да-ваемюе о«уляром, т. е. тот светаый кружок, который видеи со сто-роаеы окуяяра ирибора, если на&равмтъ объектив прибора на свет. Чтобы нзмервть его велячяяу» ирябор иадо навестн иа светпый фоя неба шт облаков-, подставяв со етороны окуляра лист мнл-лииетровой буиагн, надо стриближать его к окуявру адш удалять от гаего, ікжа на бумате не будет виден яркМ свешвой кружок, кѳторый я явдяется выходаым э^ачком (рис. О45).
|
|
|
|
Я xadhm
| в t*X9ihto в зузачая |
Рис. 1*5.
Зжэдной н выжвдаюй эрачкн оинокля
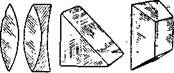
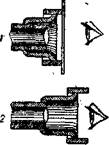
Ряс. І№. Лодввжяая обойма:
1 — вдвявэгйі; 2 — выяюшута
Кв-здр-ат диамстра выходвого зрачка пришшагот за меру отно-сительной светоеяяы гарибора. Действителъная же светосила щт-бо|>а завнокг еще й от качества линз, тж как часть света задер-живают стёкла прибора.
Отношеяие диаметра входного зрачка пр-нбора к днамегру его выходного зрачка равно увеличению прибора.
98
Прв наблюдении в прибор глаз наблюдателя должен быть ка таком расстоянии от окуляра, чтобы зрачок глаза находилсяв плоскостн выходного зрачка прибора. Для соблюдсния этого ус-ловия, a также для того, чтрбы свет сбоку не мешал наблюде-нию, приборы снабжают «раковинами», рассчитанными так, чтобы прибор можно было гюднести к глазу на иужное расстояние.
Для удобства наблюдения в противогазе на окуляры некото-рых приборов надевают подвижные обоймы: наблюдая в пррти-вогазе, обойму надо вдвинуть; при наблюдении без противога-за — выдвинуть (рис. 116). ,
Мера углов
С помощыо артиллерийских приборов измеряются углы. 06-щеприняты.е меры углов: градус (Г), минута (Г; Г = 60'), се-кунда (1"; Г = 60"). В окружноств 360°- Но в артиллерии прн-нята особая мера углов; единицей измерения является деление угломера.
Окружность делится в артиллерии- на 6 000 рав,ных частёй. Таким образом, деление арталлерийского угломера равно:
. '' 360° __ _б°___ 36!У___ „ fi,
6000 loo loo '9-
Градус составляет около 17 делений угломера (точнее 163/з делення). 100 делений угломера составляют 6°, 1000 деленнй — 60°. Прямой угол (90°) составляет 1 500 делеяяй угломера, 2 прямых (180°) —3 000 делений угломера.
Для удобства произношения принята передача одсла деленнй угломера в командах и при докладе наблтодений по телефодаому способу двумя группами, по две цифры в каждой; вместо недо-стающнх цифр ставят нули. Так, 128 делеиий угломера проиэно-сится «однн двадцать восемь», 3542 деледая угломера— «три-дцать нять с©рок два», 205 делеяий угломера —«два воль пять», 80 делений угломера — «ноль восемьдесят», " 5 деленяй угломе-ра — «ноль ноль пять» (0-05), 20Q делений угломера— «два но-ль», 3 000 делений угломера — «трвддать ноль»:
В табл. 5 ука^ан перевод делений угломера в „градусы и об-ратно.
Таблица 5
/ Перевод делений угломера в градуеы и минугы Таблица A
Делеиня углояера
0-00
1-00
2-00
3-Ѳ0
4-00
5-00
б-ОО
7-00
8-ОѲ
»-00 |
Деяенкя углояера
7*
ѲО-00 10-00 20-00 30-00 40-00 50-00
| Г Р | a д y | с ы | |||||||
| 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 60 | ■66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 |
| 120 | 126 | 132 | 138 | 144 | 150 | 156 | 162 | 168 | 174 |
| 180 | 186 | IS2 | 198 | 204 | 210 | 216 | 222 | 228 | 234 |
| 240 | 246 | 252 | 258 | 264 | 270 | 276 | 282 | 2S8 | 294 |
| 300 | ЗѲ§ | 312 | 318 | 324 | 330 | 336 | 342 | 348 | 354 |
00-00 10-00 20-00 30-00 40-00 50-00
99
Таблица Б
| Деления | 0-00 | 0-01 | 0-02 | 0-03 | 0-04 | 0-05 | 0-06 | 0-07 | 0-0S\- | 0-09 | Деления | ||||||||||
| угломера | ^І | а . и | X s S | •1 * a1 = | -'S | •1 » a' s | •1 1 4 s | X s s | u| S | £ S S | d | X 1 | угломера | ||||||||
| 0-00 0-10 0-20 0-30 0-40 0-50 0-60 0-70 0-80 * 0-90 | 0 0 1 1 2 3 3 4 4 5 | 00 36 12 48 24 00 36 12 48 24 | 0 0 1 1 2 3 3 4 4 5 | 04 40 16 52 28 04 40 15 52 28 | 0 0 1 1 2 3 3 4 4 5 | 07 43 19 55 31 07 43 19 55 31 | 0 0 1 1 2 3 3 4 4 5 | 11 47 23 59 35 11 47 23 59 35 | 0 0 1 2 2 3 3 4 5 5 | 14 50 26 02 38 14 50 26 02 38 | 0 0 1 2 2 3 3 4 5 5 | 18 54 30 05 42 18 54 30 06 42 | 0 0 1 2 2 3 3 4 5 5 | 22 58 34 10 46 22 58 34 10 46 | 0 1 1 2" 2 3 4 4 5 5 | 25 01 37 13 49 25 01 37 13 49 | 0 1 1 2 2 3 4 4 5 5 | 29 05 41 17 53 29 05 41 17 53 | 0 1 1 2 2 3 4 4 5 5 | 32 08 44 20 56 32 08 44 20 56 | 0-00 0-10 0-20 0-30 o-4o 0-50 0-60 0-70 0-80 0-90 |
Причіечание. Одно делеіше угломера (0-01) = 3,6. В таблице число минут округлено с точностью до единицы.
Работа с таблицей
Пример 1. Перевести в градусы угол 25-85 делений угломера. Сперва определяем чпсло градусов в 25-00 делениях угломера. Для этого находнм в таблице A строчку 20-00 и число, стоящее в этой строке в вертякальной графе,— 5-00; читаем число градусов: 150°; затем в таблице Б находим строчку 0-80 и число, стояшее з этой строке в вертнкальной грзфе, — 0-05, и читаем: 5°06'. Складызчем оба числа: угол 25-85 делений угломера со-держит 150o-f5o06'=155°06'.
. Пример 2. Перевести в делсния угломера угол 74 32'. В таблице A на-ходим ближайшее меньшее число градусов—72°, что соответствует 10-00+2-00 = 12-00 делений угломера. Остаётся перевести в. деления угло-мера 2°32'. Находим в таблице Б ближайшее к искомому число: 2°31', что отвечает 0-42 делепий угломера. Складываем оба полученных числа: 12-00 делений угломера + 0-42 делений угломера = 12-42 делений угломера.
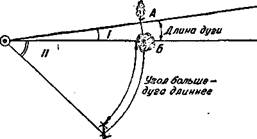
В дляне окружности её радиус укладываесся приблизительно шесть раз. Если окружность разделить на 6 ОиО равных частей, то каждая такая часть —дуга АБ (рис. 117) будет приблизитс^ь-но равна Vsooo радиуса этой окружыости:
6UU0 1000 1000К' \
|
|
>?; \Длина дуга
Расстойние больше - ді/га д/шн- нее при той тв еелиѵине угла
Рнс. 117. Зависимость всличипы дуги от велпчины ценгралыюго угла 100
Ho угол АОБ, опирающийся на дугу АБ, составляющую г/вооо окружнсгсти, или Ѵюоо радиуса этой окружности, есть деление угломера. Зйачит, углу в одно деление угломера соответствует дуга длиной в одну тысячную радиуса. Поэтому артиллерийское деление угломера обычно называюѴ тысячнои или тысячной ра-диуса. Радиусом в данном случае является расстояние от орудия пли от наблюдателя до цели или до наблюдаемого предмета. Таким образом, одно деление угломера соответствует однои ты-сячной расстоянця (дальности). Эта простая зависимостъ между угловыми и линейными веліичинами позволяет легко решать ряд практических задач. Задачи эти делятся на три основных типа.
 Задачи, решаемые с помощью тысячных м
Задачи, решаемые с помощью тысячных м
Приближенный способ
Задачи первого типа. Зная угловую велнчину предмета и дальность до него, определить его линейную вели-чину.
Пример 1. Угол, под которым с наблюда-тельного пункта (НП) виден окол іъротивника, равен 0-04, «ли, как принято говорить, угловая величика окола равна 0-04.
Расстояиие от НП до окопа 3 км. Опреде-лпть длину сжопа в метрах.
Решение. Прн расстоянии в 3 000 м угду в 1 деленне углэмера соответстпѵет линейвс« расстоявие в 3 м (3 000 л : I 000)."
| Ы*0-04 |
Угловая же величииа ѳкопа — 4 деления угломера; следователыю, его лияейная велнчвна равна, 3 л X 4 = 12 м (рис. 118).
Пример 2. От огневой позшдаи орудия до укрытия 500 м; укрытие (лес) видно вод углом в 0-40 дедений угломера. Определить выссхту укрытия.
Решение. Каждому делению угломера соот- Рис. lie. Угловая величина
ветствует лииейное расстояние в г/і.»« ог длины окопа 0-04;
500 м, или 0,001 X 500 = 500 : 1 000 = 0,5 м; 40 де- расстояниг до окопа 3 000 м;
лелиям угломепа будет, следоватсльно, отвечать линениая величина длииы
ливейная величииа в 0,5 м X 40 = 20 м. Значит, окопа 12 м *""
высота леса равняется 20 м (рис. 119).

ДвбООм
Рис. 119. Определение высоты укрытия по расстоянию до него и по его
, угловой величине
Задачи второго типа. Зная линейную величину предме-та и раестояние до него, определить его угловую величину.
ІІример 3. Лётчик-наблюдатель передал, что раарывы произошли вправо от цели. на 50 м. Далыюсть стрельбы 10 км. Определить, на какой угол по-вериуть батарею, чтобы следующие разрысы провзошли y цеди.
4 101
Рис. 121. Определение угла места цели с помощью карты
|
|
| Цель \ |
| L " 0,OOtЛ £001:700 7 Щ O * »» *" |
| =0-05 |
| La = ?s |
| /> =20м -0-S9 Д 1/гл. |
| Д= 700м |
 a "50м
a "50м
Рис. 120. Определение угловой величины от-клонения по его линей-ной величине и рас-стоянию дЬ цели
Рис. 122. Определе-ние с помощью карты -угла укрытия батареи
Решение. Одному делению утломера соответствует оДна тьгсячная дальности,
т. е. 10 0ѲО>л: 1000= 10 м (кстати следуег заметить, что в подобных случаях
производить деленне нёзачем: так как в километре 1 000 м, то тысячтгя даль-
носіи состшляет столъко же метров, сколько ки-іометров содержит дальность).
Сколышм жеч тысячным дальности, т. е. делениям угломера, соответетвуег
отклонение в 50 м> Иными словами, сколько раз уложится в 50 м" 10 А?
50 м : 10 м — 5 раз, или угловая величииа отклонеиия составит 0-05 деленнй
угломера (ноль иоль пять) (рис. 120). Значит, батарее надо скомандовать:
«Левее ноль иоль пять». |
- Приме^ 4. Высчнта^ь угол места цели, если по карте онределены: высота дели над уровием ыоря 108 м, высота батареи 92 м, дальность стрельбы 4 км.
Нешфше. Цель выше батареи иа 108 л~92 м = 16 м, причём угол места вдяи положительный (лиаия цели выше горязонта орудия). При даяыюсти стреяьбы в 4 км одяому делению ^гломера будет соогветствовагь ливейная велячиаа в 4 м; какому же углу будет соогаетсгвовать линейная велячина в 16 м, или, иначе говоря, сколько раз одна тысячиая дальяости—4 м — уло-жится в іб мі 16 м : 4 м = 4 раза. Значнт, угол места игли сосіавит jf-4 деления угломера (шиос ноль ноль четыре) (рис. 121).
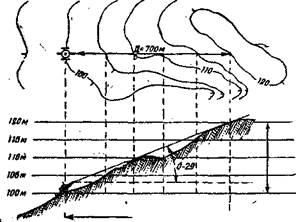
Пример 5. По карте определеио, что гребень высоты, за которой стоит батарея, иа 20 м выше батареи. Расстояние от батарен до этого гребвя 700 м. Определить угол укрытия (т. е. угол, составленнын горазоитом орудня и на-правленнем на гребеиь укрытия).
Решение. Углу в одно делеиие угломера соответствует ливеіная веяи-
чина в 0,7 м, Скольким же делеиням угдамера будет соответствовать превы-
шеиие гребия иад батареей на 20 мі Сколько раз 0,7 м уложатся в 20 л?
20 м : 0,71 м = 29 делений угломера (с округлеиием до пелых деленнй). Таким
образом, угод укрытня приблизительио равен 0-29 (ноль двадцать девять)
(рис. 122). щ^
Задачн третьеготипа. Звая угловую и линейну» вели-чину предмета, определить расстоянне до него.
Пример 6. Лес высотой в 20 м виден с НП под углом 0-04. ОиределитЬ расстояние до этого леса.
Нешение. Зиая, что одно деление угломера соответствует одной тыеячной дальности, рассуждаем так: четыре тысячнык дальвостн составляют 20 м; сле-довательно, одна тысячная дальности равиа 20 м : 4 = 5 м. Есля одна тысячиая часть дальиости равна 5 м, то вся дальность, очевидио, в тысячу раз больше, т. е. 5 км (рис. 123).
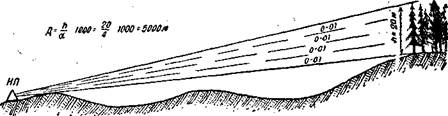
Рис. 123. Определение расстояняя до леса по лннейной и угловѳй величине
его высоты
Пример 7. Известно, что артяллерийская запряжка имеет в длину 15 м. При выезде . неприятельской батареи на позицию одиа нз запряжек неосто-рожио выехала на гребень и была при этом видиа под углом в' 0-05. Оире-делить расстоянае от НП до выезжающей неприятельской батареи.
103
 Решечие. Рассуждаем, как в примере 6. Пять тысячных дальности составляюг 15 м; зна-чйт, одиа тысячная дальиости равиа 15 м : 5=3 te; вся дальиость в тысячу раз больше, чем одна её тысячная часть, т. е. равиа 3 км (рис. 124).
Решечие. Рассуждаем, как в примере 6. Пять тысячных дальности составляюг 15 м; зна-чйт, одиа тысячная дальиости равиа 15 м : 5=3 te; вся дальиость в тысячу раз больше, чем одна её тысячная часть, т. е. равиа 3 км (рис. 124).
| Я 'jr-WOO* |
Более точный способ решения"задач
' на тысячную .
| 1000= |
Подобные вычисления не вполяе точны; при более точиом вычпслении получается несколько ииое соотношение между линенными и угловыми велнчинами. Одному делеяию угломера еоответ-ствует величииа:
2kR 6,28 R
gTJ00 = -gффT =0,00104666.« ^0,001047/? =
=t: 0,00105 R, или приблизительно qkk • R.
| Рис. 124. Определение рас-стояния до неприятельской батареи по линейной и угло-вой величине орудийной запряжки |
Для приближёиных лолевых расчётов такая мелкая неточность ие имеет знаіения.
Если же иужно добиться большей точностй расчёта, то необходимо учесть следующее: счи-тая одно деление угломера соответствующим одной тысячной дальности (0,001 Д), мы допу-скаем ошибку приблизительно ва 5% (точиее на 4,666%); это видпо из приведённого выше расчёта. При этом мы всегда будем получать преувеличенную против де^твит&льной угловую величину ' (так как линейкую величину предмета делш^рі 0.001Д, a не на 0.00105Д, как бы сле-довало). Чтобы исправить эту постоянную ошибку, достаточио получениый ре-зультат вычисления уменьшить иа 5%.
Пример. Превышеиие цели иад батареей 180 м. Дальность стрельбы 3 км. Применяя полевой расчёт, получаем величину угла места цели 180 м:Ъ te — = 0-60 делеиий угломера. Чтобы подучить эту ведичииу с большей точ-ностью, иадо уменыішть её на 5%.
5% от 60 составит ~\Ш~3. Значит, при более точном вычисленни
угол места в,ели равеи не 0-60 делений угломера, a 0-60—-0-03 = 0-57 деленнй угломера.
Это так называемая пятипроцентная поправка к велнчиие угла места цели, определённой по упрощёниой полевой формуле. Она вводится только в тех сдучаях, когда иужна большая точвость расчётов (при полиой подготовке данных).
Г л a в a 7 НАВОДКА ОРУДИЯ Понятие о наводке
Раздичают горизокгалъную и вертикальную наводку орудия.
Горизонтальнон наводкой называют придание орудию направ-
дения на цель. '
Вертикальной наводкой называют придание орудию угла воз-вышения.
Угол возвышения является суммой углов прицеливания и м*е-ста целн. Поэтому н вертикальная наводка сводится к двум дей-ствиям: а) прнданию орудию угла прицеливания с помощью при-цела, б) приданию орудию угла места цели с помощью- уровня. 104
Вертикальная наводка
Устройство прицелов y разных орудий очень разнообразно',
однако суть их устройства сводится к двум способам учёта углов
прицелнвакия. У одних систем шкала прицела разделена на оди-
наковые деления— тысячные. . Увеличив угол прицеливания на
одну тысячную, мы увеличим и дальность падения снаряда 2, но
это увеличение будет различиым при разных зарядах, снарядах и
на разных дальностях. Так, прибавив y 122-мм пушки к углу при-
целиваная одну тысячную на малой дальности, мы увеличим
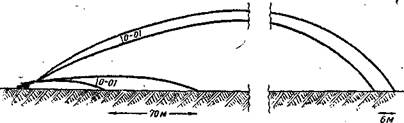
дальность полёта снаряда примерно на 70 м, a на предельной
дальности — всего лишь на 6 м (рис. 125). •
A J
Рис. 125. Изменение далыюсти от изменения установки прицела
на одну тысячную:
a — Ha мадой дальности; 6 — на бодьшой дальности
Такая нарезка прицела удобиа для наводчика, которому всег-да.надо иметь дело с одной шкалой прицела. Но зато^ стреляю-щий должен всегда пользоваться Таблицами стрельбы, потому что невозможно помнить наизусть, какая дальность отвечает той или иной установке прицела при том или ином снаряде и заряде.
|
|
| Рис. 126. Боковой уровень и его шкала |
У других орудий, наоборот, предусмотрены удобства стреляю-щего: прицел имеет несколько шкал, от-. дельно для каждого снаряда и заряда. Деления на этих шкалах различны по своей величине для разных дальносі^й, снарядов, зарядов, но обладают тем свойством, что изменение установки при-цела на однодсление изменяет дальность радвния снаряда на 50 м. ' Величина, на которую изменяется дальность падеиия снаряда от изменения установки прицела на одно деление, со-кращенно называется в артиллерии XX (читается: «дельта икс»). Таким обра-зом, y одних оруднй XX — величина пе-ременная, y других оруддй XX—вйличина постоянная, равная50лг.
Углы Места цели учитываются y всех оруднй с помощью уста-новки бокового уровня (рис. 126).
1 Изучать устройство прицела следует иа конкретлых системах, по их
описаниям.
2 При углах менее 45°.
3 У 45-лоі и 57-мм проіивотанковых пушек — 100 м.
105
Если угол места целя равен нулю, остается основная установ-ка уровия 30-00 (традцать нояь) '; если угол места цели положи-'тельный, его велнчнну прибавляют к основной установке; напри-мер, еслй угол места цели равен +0-04, то расчёт такой:
* зо-оо :+; 0-04 = 30-042.
В этом случае надо скомандовать: «Уровень тридцать ноль четыре». Если же угал места цели отрицательный, то величину его надо отнять от основнон установки; например, при отрнцательном угле места целн в 0-06 надо сделать такой•подсчёт:
 30-00 — 0-06 = 29-94,
30-00 — 0-06 = 29-94,
и скомандовать: «Уровень двадцать девять девяносто четыре».
Поставвв на шкале бокового уровня и иа шкале прицела скомандованные деления, на-водчяк должеи подогнать на середнну пузы-рек уровня, работая подъёмным механнзмом; в этом и заключается вертйкальная наводка орудия по уровню.
При изменении- установки уровия на одно деление высота допадания изіленяется при-мерно на Ѵіооо дальвоети; дальность же паде-ния снаряда изменяется различно на разных дальностях стрельбы (рис. 125).
Дата: 2019-02-02, просмотров: 931.