Файлы-функции широко используются в ML. Пользователь может с их помощью описывать свои функции для многократного выполнения, также с их помощью могут решаться следующие задачи:

1. построение графика функций;

2. численное интегрирование;

3. нахождение корней трансцендентного уравнения;

4. поиск экстремумов функци;

5. решение систем дифференциальных уравнений.

Построение графика.

График функции на заданном отрезке, символьное выражение (формула) которой записано в файле-функции, можно построить, используя команду:

fplot ( fun , interval ), где

fun – имя функции или символьное выражение, задающее формулу вычисления;

interval – отрезок, который задается вектором из двух значений: начального и конечного значения отрезка.

В качестве примера построим график функции х²-1 на отрезке от 0 до p. Для функции х²-1 напишем файл-функцию. В текстовом редакторе наберем следующий текст:

function f = func ( x )

f = x .^2-1;

Сохраним его в файле с именем func.m.

Для построения графика выполним команду:

>> fplot('func',[0 pi])

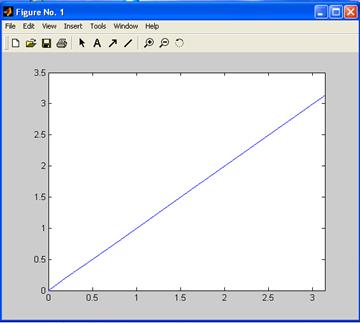
Или используем вместо имени функции символьное выражение:

>> fplot('sin(x)',[0 pi])

Вычисление интеграла.

Самым простым численным методом нахождения определенных интегралов является метод трапеций, который реализован функцией trapz ( x , y ), где x и y – вектора, задающие значения аргумента и функции в пределах интегрирования. Для ее использования не требуется оформление подинтегральной функции в качестве файла-функции.

Вычислим интеграл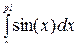

>> x=0:pi/100:pi;

>> y=sin(x);

>> z=trapz(x,y);

z =

1.9998

Получили приближенное значение интеграла. Увеличив шаг интегрирования до pi/1000, получим более точное значение – 2.

Более точные методы реализованы в функциях quad , quad 8, quadl .

Функция quad основана на квадратурной формуле Симпсона, а функция quadl предназначена для вычисления интеграла по более точным формулам Гаусса-Лейбница. Функция quad 8 реализует метод Ньютона-Котеса восьмого порядка. Все три функции имеют одинаковый набор параметров.

[i, n]=quad(fun, a, b, tol, trace), где

fun - имя файла-функции или символьное выражение, определяющее подинтегральную функцию (оно должно быть заключено в апострофы);

a , b – пределы интегрирования;

tol – погрешность вычислений;

trace – признак; если его значение равно 1, то при выполнении функции строится график подинтегральной функции, если 0, то не строится. Последние два параметра являются необязательными.

i – значение интеграла;

n – количество значений функции, которое потребовалось вычислить для нахождения значения интеграла.

>> [i, n]=quad8('func', 0, pi, 1e-8, 1)

i =

7.1938

n =

33

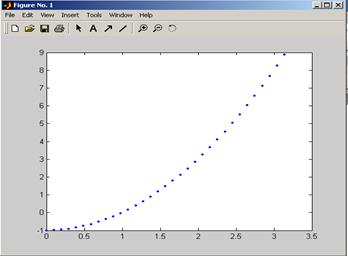
При использовании этих численных методов задаётся требуемая точность вычислений, а шаг подбирается автоматически (в отличие от функции trapz). По умолчанию точность равна 10^-6.

Имя функции может быть задано символьным выражением.

>> [i,n]=quad8('sin(x)', 0, pi, 1e-8, 0)

i =

2.0000

n =

33

Такой же результат получим, если не укажем два необязательных параметра:

>> [i, n]=quad8('sin(x)', 0, pi )

i =

2.0000

n =

33

Тот же интеграл можно вычислить с использованием функции quadl:

>> [i, n]=quadl('sin(x)',0,pi,1e-8,0)

i =

2.0000

n =

48

Для достижения одной и той же точности понадобилось различное количество вычислений. Можно при вызове функции не указывать выходной параметр n. Тогда команда обращения к функции будет:

>> i=quadl('sin(x)', 0, pi, 1e-8, 0)

i =

2.0000

В этом случае не используется количество значений функции, которое потребовалось вычислить для нахождения значения интеграла.