Задание 1. Вывести формулу для определения моментов инерции тел А и В относительно указанных осей. (Номера тел необходимо взять из табл. 1.2.1 согласно своему варианту. Названия тел и осей вращения, относительно которых необходимо найти момент инерции, - из табл. 1.2.2.)
Таблица 1.2.1
| Номер варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| А | 1 | 2 | 3 | 4 | 5 | 6 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 |
| В | 7 | 8 | 9 | 10 | 11 | 12 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Таблица 1.2.2
| № п/п | Название тела | Ось, относительно которой определяется момент инерции | Конечная формула момента инерции |
| 1. | полый цилиндр массой m, внутренним радиусом r и внешним – R | проходит через центр, перпендикулярно плоскости основания |  m(r2+R2) m(r2+R2)
|
| 2. | тонкостенный цилиндр массой m и радиусом R | проходит через центр, перпендикулярно плоскости основания | mR2 |
| 3. | однородный цилиндр массой m и радиусом R | проходит через центр, перпендикулярно плоскости основания |  mR2 mR2
|
| 4. | обруч массой m и радиусом R | проходит через центр, перпендикулярно плоскости основания | mR2 |
| 5. | сплошной диск массой m и радиусом R | проходит через центр, перпендикулярно плоскости основания |  mR2 mR2
|
| 6. | сплошной диск массой m и радиусом R | совпадает с диаметром диска |  mR2 mR2
|
| 7. | сплошной шар массой m и радиусом R | совпадает с диаметром шара |  mR2 mR2
|
| 8. | тонкостенный шар массой m и радиусом R | совпадает с диаметром шара |  mR2 mR2
|
| 9. | однородный тонкий стержень массой m и длиной l | проходит через центр, перпендикулярно стержню | 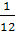 ml2 ml2
|
| 10. | однородный тонкий стержень массой m и длиной l | проходит через центр и составляет с направлением стержня угол α | 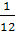 ml2sin2α ml2sin2α
|
| 11. | однородный тонкий стержень массой m и длиной l | проходит через конец стержня, перпендикулярно стержню |  ml2 ml2
|
| 12. | однородный конус массой m и радиусом основания R | проходит через центр, перпендикулярно плоскости основания | 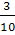 mR2 mR2
|
Примечание: конечный результат сравнить с табличными формулами моментов инерции соответствующих тел А и В, приведенными в табл. 1.2.2.
Задание 2. С наклонной плоскости длиной L, составляющей с горизонтом угол α, скатываются без скольжения тела Б и С, имеющие одинаковые массы (m = 3 кг) и радиусы (R = 10 см). Для каждого тела найти:
а) ускорение;
б) линейную скорость в конце наклонной плоскости;
с) полную кинетическую энергию.
Примечание: В табл.1.2.3 каждое тело расположено под определенным номером. Зная номер своего варианта, по табл. 1.2.4 определите название тел Б и С, угол наклона плоскости α и длину плоскости L . Например, для первого варианта: тело Б – однородный цилиндр, тело С – тонкостенный цилиндр, α = 30°, L = 6 м.
Таблица 1.2.3
| № п/п | Название тел |
| 1 | Однородный цилиндр |
| 2 | Тонкостенный цилиндр |
| 3 | Обруч |
| 4 | Сплошной диск |
| 5 | Сплошной шар |
| 6 | Тонкостенный шар |
Таблица 1.2.4
| Номер варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Тело Б | 1 | 3 | 5 | 1 | 3 | 5 | 1 | 3 | 5 | 1 | 3 | 5 | 1 | 3 |
| Тело С | 2 | 4 | 6 | 2 | 4 | 6 | 2 | 4 | 6 | 2 | 4 | 6 | 2 | 4 |
| α, град | 30 | 45 | 60 | 30 | 45 | 30 | 45 | 60 | 30 | 45 | 60 | 30 | 45 | 60 |
| L, м | 6 | 8 | 5 | 10 | 7 | 6 | 10 | 6 | 8 | 5 | 10 | 7 | 6 | 10 |
Контрольные вопросы:
1. Что такое момент инерции?
2. Какова роль момента инерции во вращательном движении?
3. Вывести формулу кинетической энергии тела, вращающегося вокруг неподвижной оси.
4. Сравнить скорости и ускорения поступательного движения при скатывании полых и сплошных тел одинаковой геометрической формы и массы.
5. Для какого тела на долю вращательного движения приходится большая энергия – сплошного или полого?
Дата: 2019-02-02, просмотров: 434.