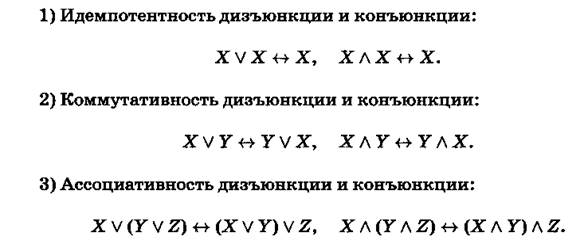

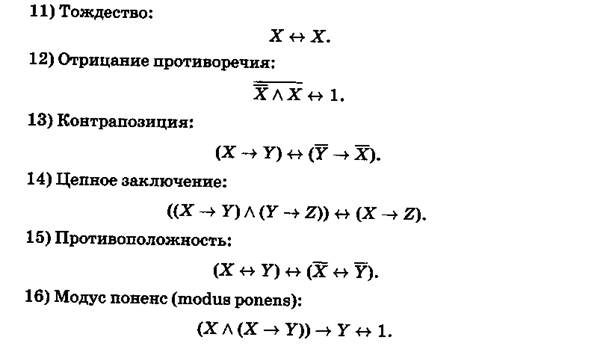
Сформулированные законы легко проверить с помощью таблицы истинности.

Индивидуальные задания

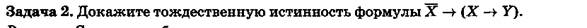
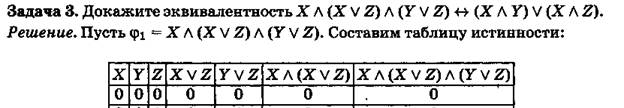
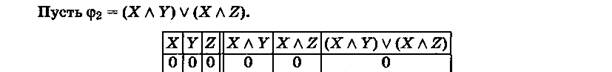

Задача 5. Таблица истинности высказывания, составленного из двух простых высказываний, состоит из четырех строк; а таблица истинности высказывания, составленного из трех простых высказываний, – из восьми строк. Сколько строк должна иметь таблица истинности высказывания, составленного из четырех простых высказываний? Сколько – из пяти? Сколько – из n? Укажите способ систематической записи таблиц истинности для произвольного п?
Указание. Для систематической записи таблиц истинности для произвольного п можно применить метод «последовательного половинного деления столбцов» – столбец первой переменной делят пополам и заполняют верхнюю половину нулями, а нижнюю половину – единицами, затем каждую половину второго столбца делят пополам и опять заполняют полученные половины нулями и единицами и т. д.

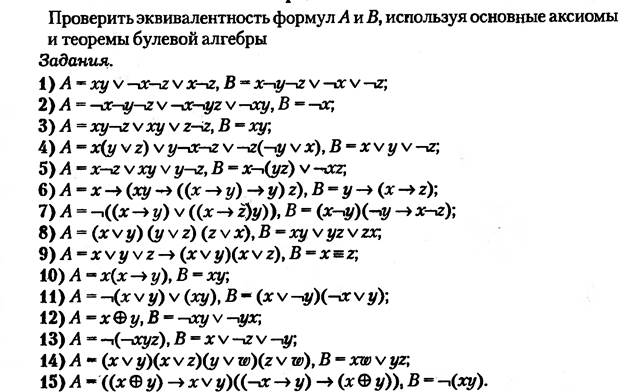
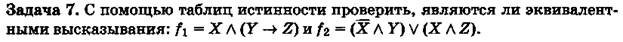
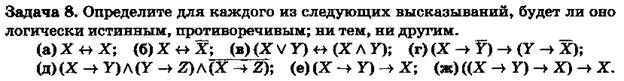
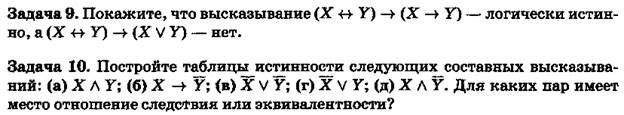

Задача 15. Чему эквивалентна конъюнкция контрапозиции и ее конверсии?
Задача 16. Докажите, что отрицание высказывания: «X есть необходимое и достаточное условие для Y» эквивалентно высказыванию: «X есть необходимое и достаточное условие для Y».
Задача 17. Докажите, что контрапозиция эквивалентна первоначальной импликации.
Задача 18. Пусть X означает: «Я сдам этот экзамен»; a Y: «Я буду регулярно выполнять домашние задания». Запишите в символической форме следующие высказывания:
а) «Я сдам этот экзамен только в том случае, если буду регулярно выполнять домашние задания».
б) «Регулярное выполнение домашних заданий является необходимым условием для того, что я сдам этот экзамен».
в) «Сдача этого экзамена является достаточным условием того, что я регулярно выполнял домашние задания».
г) «Я сдам этот экзамен в том и только в том случае, если я буду регулярно выполнять домашние задания ».
д) «Регулярное выполнение домашних заданий есть необходимое и достаточное условие для того, чтобы я сдал этот экзамен».
Выясните, какому из перечисленных высказываний соответствуют следующие символические формы: 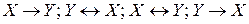
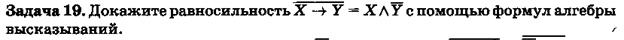
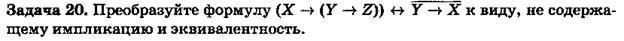



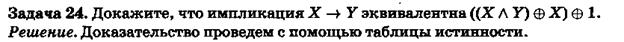
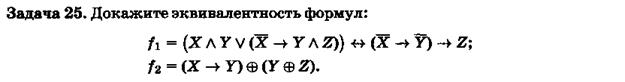
Задача 26


Определить двумя способами, являются ли формулы тавтологиями для следующих заданий.
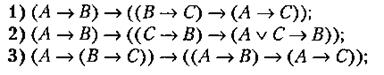
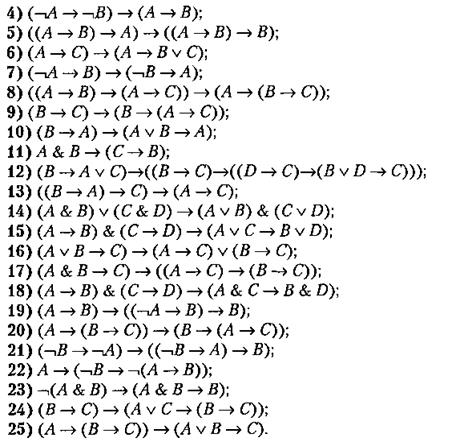
Индивидуальные задания
| Вариант | задание1 | задание 2 | задание3 | задание4 | задание5 | задание6 | задание7 |
| 1 | 7 | 6(4) | 8(в) | 12(б) | 19 | 21(а) | 26(10) |
| 2 | 1 | 6(11) | 10(б,в) | 13 | 20 | 24 | 26(7) |
| 3 | 4 | 6(9) | 8(е) | 16 | 18(а,в) | 23(а) | 26(13) |
| 4 | 7 | 6(3) | 10(а,г) | 12(а) | 19 | 24 | 26(18) |
| 5 | 1 | 6(14) | 8(г) | 17 | 18(г,д) | 23(б) | 26(6) |
| 6 | 3 | 6(12) | 11 | 14 | 20 | 21(б) | 26(17) |
| 7 | 3 | 6(5) | 8(б) | 15 | 19 | 21(а) | 26(8) |
| 8 | 2 | 6(8) | 10(д,в) | 12(б) | 20 | 22(б) | 26(16) |
| 9 | 3 | 6(7) | 8(ж) | 17 | 18(б,г) | 23(б) | 26(14) |
| 10 | 7 | 6(13) | 11 | 14 | 19 | 25 | 26(5) |
| 11 | 2 | 6(2) | 10(д,б) | 15 | 18(а,г) | 21(в) | 26(12) |
| 12 | 4 | 6(6) | 8(д) | 12(а) | 19 | 25 | 26(15) |
| 13 | 2 | 6(15) | 9 | 16 | 20 | 23(б) | 26(9) |
| 14 | 3 | 6(10) | 10(а,г) | 15 | 20 | 21(в) | 26(11) |
| 15 | 1 | 6(1) | 8(а) | 13 | 18(б,в) | 22(а) | 26(4) |
Дата: 2019-02-02, просмотров: 1605.