ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ
Имени В.Я.ГОРИНА»
Кафедра информатики и информационных технологий
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ
к выполнению лабораторно-практических и самостоятельных работ
по дисциплине
«ИНФОРМАТИКА И ПРОГРАММИРОВАНИЕ»
для студентов экономического факультета
Направления «Прикладная информатика»
Белгород 2014
УДК 681.3.06 (076)
БК 32.81
М 54
Методические указания и задания к выполнению лабораторных работ по дисциплине «Информатика и программирование» для студентов направления «Прикладная информатика» – Белгород: Издательство ФГБОУ ВО Белгородский ГАУ, 2014. – 114 с.
Разработчик: к.т.н. Игнатенко В.А.
Рецензент: к.т.н. Петросов Д.А.
Рассмотрена на заседании кафедры информатики и информационных технологий «____»______________2014 г., протокол №_____
Зав.кафедрой _______________________ Петросов Д.А.
Одобрена методической комиссией экономического факультета
«____»______________2014 г., протокол №_____
Председатель методической комиссии
экономического факультета ___________________Черных А.И.
© Федеральное государственное бюджетное образовательное учреждение высшего образования Белгородский государственный аграрный университет имени В.Я. Горина
Лабораторная работа № 1
Логические операции. Основные законы
Цель работы: Изучить логические операции и основные законы, определяющие свойства введенных логических операций.
Теоретические сведения.
Математическая логика – это анализ методом рассуждений, при этом в первую очередь исследуются формы рассуждений, а не их содержание, т. е. математическая логика исследует соотношения между основными понятиями математики, на базе которых доказываются математические утверждения. Простейшую из формальных логических теорий называют алгеброй высказываний, поэтому начнем знакомство с элементами математической логики с такого понятия, как высказывание, которое лежит в основе логико-математической теории дискретной математики.
Составные высказывания
Высказыванием называется повествовательное предложение, о котором в данной ситуации можно сказать, что оно истинно или ложно, но не то и другое одновременно.
Приведем примеры высказываний.
Пример 1. Волга впадает в Каспийское море.
Пример 2. Два больше трех.
Первое высказывание является истинным, а второе – ложным.
Таким образом, высказывание обладает свойством представлять истину или ложь, поэтому на высказывание можно смотреть как на величину, которая может принимать только одно из двух значений: «истина», «ложь».
Поставим в соответствие высказыванию логическую переменную х, которая принимает значение 1, если высказывание истинно, и 0, если высказывание ложно.
Мы не будем исследовать внутреннюю структуру высказываний, потому что такое исследование оказывается достаточно трудным и относится скорее к лингвистике, чем к математике. Поэтому мы будем поступать так, как если бы мы знали все о простых высказываниях, и будем изучать лишь их сочетания, т. е. как различными способами из отдельных высказываний можно построить новое высказывание.
Это новое высказывание называется составным, в то время как высказывания, из которых оно образовано, называются его простыми составляющими или компонентами. Любое высказывание, даже такое, которое на самом деле является сложным, может быть использовано в качестве одного из простых составляющих какого-то другого составного высказывания.
Простейшие связки
Значение истинности составного высказывания определяется значениями истинности его компонент.
Высказывания будем обозначать прописными буквами латинского алфавита Х, Y, Z, ....
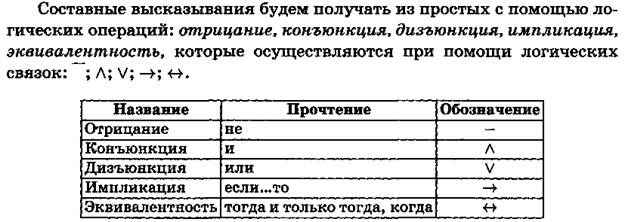
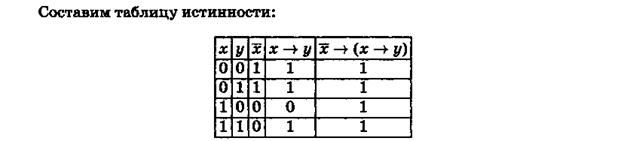
При рассмотрении той или иной связки мы хотим знать, каким именно образом истинность составного высказывания, порожденного этой связкой, зависит от истинности его компонент. Очень удобно изображать эту зависимость, пользуясь таблицами истинности, которые называются также интерпретациями логических операций. Каждой строке таблицы истинности взаимно однозначно соответствует набор составляющих высказываний и соответствующее значение составного высказывания. Наборы из нулей и единиц, соответствующих составляющим высказываниям, в каждой строке таблицы истинности имеют стандартное расположение, т. е. расположены в лексикографическом порядке (порядке возрастания).
Пусть даны два произвольных высказывания X и Y.
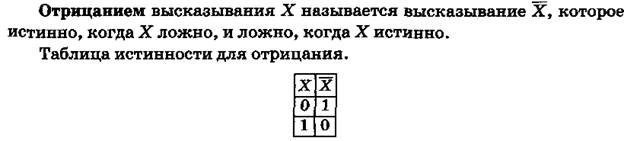
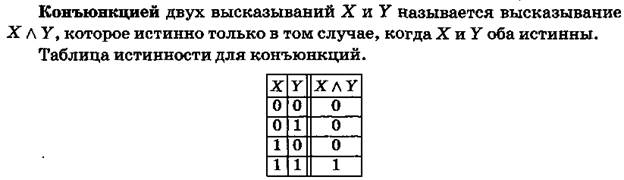
Для образования составных высказываний наряду с единичным использованием каждой основной связки можно пользоваться основными связками многократно, получая более сложные составные высказывания – аналогично тому, как с помощью основных арифметических операций образуются сложные алгебраические выражения.
Например, составными будут высказывания:
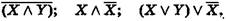
Их следует читать «изнутри наружу», подобно алгебраическим выражениям, в которых сначала группируются величины, заключенные в самые внутренние скобки, затем эти скобки в свою очередь группируются и т. д. Если скобок нет, то операции надо выполнять в следующем порядке: конъюнкция, дизъюнкция, импликация, эквивалентность, отрицание. Каждое составное высказывание имеет свою таблицу истинности, которая может быть построена стандартным образом.
Другие связки
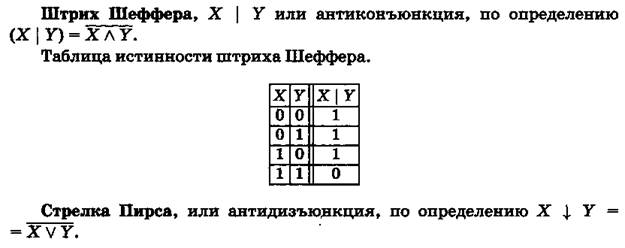
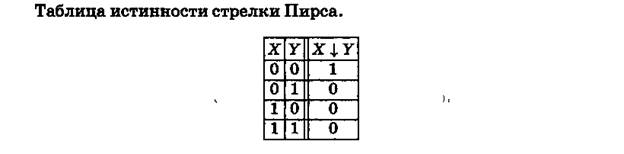
Задача 26
Лабораторная работа 2
Теоретические сведения.
Многочлены Жегалкина
Согласно сформулированным утверждениям, можно говорить, что система булевых функций полна. Тогда любую булеву функцию можно представить в виде многочлена от своих переменных и такой многочлен называется многочленом Жегалкина.
Многочленом Жегалкина называется многочлен, являющийся суммой константы и различных одночленов, в которые каждая из переменных входит не выше, чем в первой степени.
Сформулируем алгоритм построения многочлена Жегалкина. Выше было указано, что любую функцию, отличную от константы 0, можно представить в виде СДНФ. Если сравним таблицы истинности
Индивидуальные задания
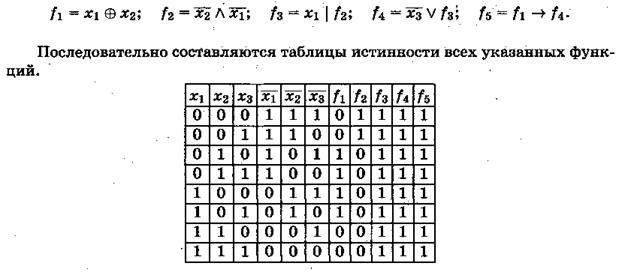
Лексикографическое упорядочение наборов в таблице истинности булевой функции позволяет задать функцию двоичным набором длины 2n, который будем обозначать буквой F . Двоичный набор данной функции F = 11111111. Отметим, что двоичный набор определяет булеву функцию в том и только в том случае, когда его длина есть степень двойки, а соответствующий показатель степени определяет число переменных данной функции.
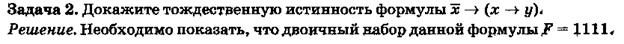
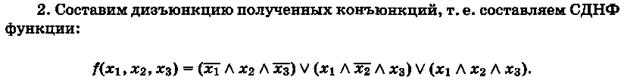
Задача 16
Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции.
Индивидуальные задания
| Вариант | задание1 |
| 1 | 16(3) |
| 2 | 16(6) |
| 3 | 16(10) |
| 4 | 16(5) |
| 5 | 16(14) |
| 6 | 16(12) |
| 7 | 16(1) |
| 8 | 16(9) |
| 9 | 16(13) |
| 10 | 16(15) |
| 11 | 16(2) |
| 12 | 16(7) |
| 13 | 16(4) |
| 14 | 16(8) |
| 15 | 16(11) |
Контрольные вопросы
1. Что называется высказыванием?
2.Приведите пример высказываний. Какое высказывание называется истинным, а какое ложным?
3.Что называется составным высказыванием?
4.Перечислите виды логических операций над высказываниями и сформулируйте их определение.
5.Какие основные символы используются в теории высказываний?
6.Какие связки простейшие? Назовите другие связки.
7.Что такое таблица истинности высказывания и как она строится? Как еще называется эта таблица?
8.Какие существуют логические отношения между высказываниями?
9.Перечислите варианты импликации.
10.Сформулируйте основные законы алгебры высказываний. Как их доказать?
11.Что такое булева функция?
12.Как строится таблица истинности для булевых функций?
13.Что такое ДНФ и КНФ?
14.Дайте определение совершенного одночлена.
15.Приведите правило преобразования формул в СДНФ и СКНФ.
16.Как булевы функции связаны с формулами алгебры высказываний?
17.Дайте определение многочлена Жегалкина и сформулируйте теорему Жегалкина.
18.Сформулируйте первый алгоритм построения многочлена Жегалкина булевой функции.
19.В чем состоит метод неопределенных коэффициентов для построения многочлена Жегалкина?
20.Какой многочлен Жегалкина называется нелинейным?
21.Каков алгоритм определения линейности (нелинейности) булевой функции?
Лабораторная работа №3
Теоретическая часть.
Алгоритм Шеннона-Фено. Суть этого алгоритма, при использовании двоичного кода (объем алфавита элементов символов кода равен 2), заключается в следующем.
Все символы алфавита источника сообщений ранжируют, т. е. располагают в порядке убывания вероятностей их появления. Затем символы алфавита делятся на две группы приблизительно равной суммарной вероятности их появления. Все символы первой группы получают «0» в качестве первого элемента кодового символа, а все символы второй группы — «1». Далее группы делятся на подгруппы, по тому же правилу примерно равных суммарных вероятностей, и в каждой подгруппе присваивается вторая позиция кодовых символов. Процесс повторяется до закодирования всех символов алфавита кодируемого источника сообщений. В кодовый символ, соответствующий последней группе, добавляется в качестве последнего элемента «0» для того, чтобы начальный элемент символов кода не совпадал с конечным, что позволяет исключить разделительные элементы между символами кода.
Таблица 1 иллюстрирует процесс построения кода Шеннона–Фено на примере источника сообщений, алфавит которого состоит из восьми символов.
Таблица 1
| Номер | Символы | Вероятности | Номера | Кодовые |
| символа. (i) | алфавита. (mi) | (Рi ). | Разбиений. | Символы. |
| 1 | m1 | 1/2 |
I
II III
IV
V
VI VII | 0 |
| 2 | m2 | 1/4 | 10 | |
| 3 | m3 | 1/8 | 110 | |
| 4 | m4 | 1/16 | 1110 | |
| 5 | m5 | 1/32 | 11110 | |
| 6 | m6 | 1/64 | 111110 | |
| 7 | m7 | 1/128 | 1111110 | |
| 8 | m8 | 1/256 | 11111110 |
Представляет интерес сравнение эффективного кодирования равномерным кодом и неравномерным кодом по алгоритму Шеннона–Фено.
В качестве примера рассмотрим предложенный выше (Табл. 1) источник сообщений с объемом алфавита равным 8 и соответствующими вероятностями появления отдельных символов (Pi). Для кодирования используем двоичный код ( k = 2).
Энтропия рассмотренного источника сообщений (H и) определяется по формуле Шеннона:
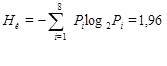(бит/символ).
Максимально же возможное значение энтропии источника сообщений (H u.max), при условии равновероятного и взаимно независимого появления символов, находится по формуле Хартли:
.
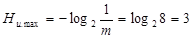Следовательно, избыточность рассматриваемого источника сообщений (R и) может быть найдена из соотношения:
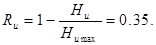
Средняя длина неравномерного кода (п Н) определяется выражением:
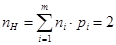, (2.7)
где пi — значность i - го кодового символа, соответствующего символу алфавита m i .
Избыточность неравномерного кода ( R НК ) определим из соотношения:
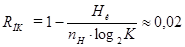
Энтропия элементов символов эффективного неравномерного кода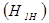 
может быть легко найдена:
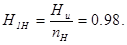(бит/элемент символа кода). (2.8)
Алгоритм Хаффмена. Суть этого алгоритма, при использовании двоичного кода, состоит в следующем. Все символы алфавита источника сообщений ранжируют, т.е. выписывают в столбец в порядке убывания вероятностей их появления. Два последних символа объединяют в один вспомогательный символ, которому приписывают суммарную вероятность.
Вероятности символов, не участвовавших в объединении, и вероятность вспомогательного символа вновь ранжируют, т.е. располагают в порядке убывания вероятностей в дополнительном столбце и два последних символа объединяются. Процесс продолжается до тех пор, пока не получим единственный вспомогательный символ с вероятностью равной единице. Пример кодирования по алгоритму Хаффмена приведен в таблице 2.
Таблица 2
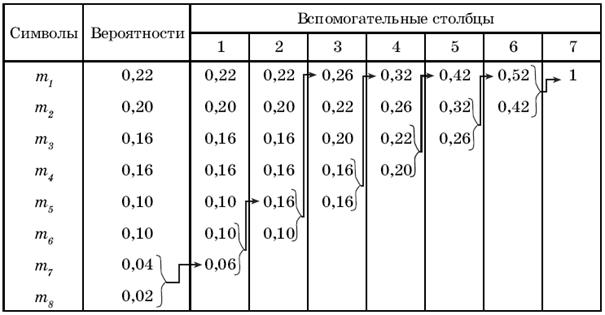
На рис. 1 показан граф кодирования (кодовое дерево), который иллюстрирует ранжирование символов на группы и отдельные символы, причем из точки, соответствующей вероятности 1, направляем две ветви: одной из них (с большей вероятностью) присваиваем символ 1, а второй – символ 0.
|
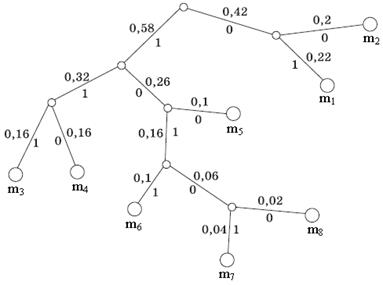
Рис 1. Граф кодирования по алгоритму Хаффмена
Различные символы, генерируемые источником сообщения, и соответствующие им кодовые символы представлены в таблице 3.
Таблица 3.
| m1 | m2 | m3 | m4 | m5 | m6 | m7 | m8 |
| 01 | 00 | 111 | 110 | 100 | 1011 | 10101 | 10100 |
Этот алгоритм можно использовать и при ином числовом основании кода, а также использовать блоки, как это рассмотрено в алгоритме Шеннона-Фено.
Эффективность рассмотренных алгоритмов достигается благодаря присвоению более коротких кодовых комбинаций (кодовых символов) символам источника сообщений, вероятность которых более высока, и более длинных кодовых комбинаций - символам источника сообщений с малой вероятностью. Это ведет к различиям в длине кодовых символов и, как следствие, к трудностям при их декодировании. Для разделения отдельных кодовых символов можно использовать специальный разделительный элемент, но при этом существенно снижается эффективность кода, т.к. средняя длина кодового символа фактически увеличивается на один элемент символа кода.
Целесообразнее обеспечить декодирование без введения дополнительных элементов символов. Этого можно добиться, если в эффективном коде ни одна кодовая комбинация не будет совпадать с началом более длинной кодовой комбинации. Коды, удовлетворяющие этому условию, называют префиксными кодами (префиксом или началом называют первый элемент в кодовом символе, а последний элемент – окончанием или постфиксом).
Легко заметить, что коды, построенные по алгоритмам Шеннона–Фено или Хаффмена, являются префиксными.
Содержание работы. По номеру в списке группы ( k ) из Таблицы 4 выбрать закон распределения вероятности появления символов источника дискретных сообщений с объёмом алфавита М=8.
Произвести эффективное кодирование заданного источника дискретных сообщений по алгоритму Шеннона-Фено и по алгоритму Хафмена.
Рассчитать для построенных на основе этих алгоритмов кодов:
а). среднюю длину неравномерного кода (n н);
б). избыточность неравномерного кода(R нк);
в). энтропию элементов символов полученных кодов(H 1н);
Сравнить полученные результаты с соответствующими параметрами равномерного двоичного цифрового кода.
Таблица 4.
| mi | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| m1 | 0.10 | 0.18 | 0.07 | 0.65 | 0.55 | 0.60 | 0.01 | 0.15 | 0.30 | 0/01 |
| m2 | 0.51 | 0.10 | 0.03 | 0.05 | 0.05 | 0.06 | 0.02 | 0.10 | 0.20 | 0.05 |
| m3 | 0.02 | 0.47 | 0.11 | 0.06 | 0.16 | 0.02 | 0.02 | 0.30 | 0.10 | 0.03 |
| m4 | 0.10 | 0.07 | 0.33 | 0.03 | 0.03 | 0.10 | 0.15 | 0.35 | 0.05 | 0.02 |
| m5 | 0.02 | 0.03 | 0.25 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.15 | 0.10 |
| m6 | 0.20 | 0.02 | 0.01 | 0.15 | 0.02 | 0.15 | 0.45 | 0.02 | 0.10 | 0.14 |
| m7 | 0.01 | 0.04 | 0.17 | 0.02 | 0.02 | 0.03 | 0.30 | 0.01 | 0.07 | 0.25 |
| m8 | 0.04 | 0.09 | 0.03 | 0.02 | 0.15 | 0.05 | 0.03 | 0.05 | 0.03 | 0.40 |
Контрольные вопросы.
- Какой вид кодирования называют эффективным и в чем его специфика?
- Что такое избыточность кодов?
- Какие коды называются равномерными?
- На каких принципах основано построение эффективных кодов при неравновероятном появлении символов сообщения?
- Принцип построения эффективного кода по алгоритму Шеннона-Фено.
- Принцип построения эффективного кода по алгоритму Хафмена.
Лабораторная работа № 4
Теоретические сведения
Операторы повтора
Если в программе возникает необходимость неоднократно выполнить некоторые операторы, то используются операторы повтора (цикла). В языке Паскаль различают три вида операторов цикла: while, repeat, for. Они используются для организации циклов различных типов. Выражение, управляющее повторениями, должно иметь булевский тип.
Если число повторений оператора (составного оператора) заранее неизвестно, а задано лишь условие его повторения (или окончания), используются операторы while, repeat. Оператор for используется, если число повторений заранее известно.
Оператор повтора for
В случаях, когда число повторений может быть заранее известно, для организации циклической обработки информации применяется оператор повтора for. Часто этот оператор повтора называют оператором цикла с параметром, так как число повторений задается переменной, называемой параметром цикла, или управляющей переменной. Оператор повтора for состоит из заголовка и тела цикла.
Он может быть представлен в двух форматах:
• for < параметр цикла > := <S1> to <S2> do < оператор >;
• for < параметр цикла > := <S1> downto <S2> do < оператор >;
где Sl и S 2 — выражения, определяющие соответственно начальное и конечное значения параметра цикла;
for ... do — заголовок цикла;
<оператор> — тело цикла.
Тело цикла может быть простым или составным оператором. Оператор for обеспечивает выполнение тела цикла до тех пор, пока не будут перебраны все значения параметра цикла от начального до конечного.
Заголовок оператора повтора for определяет:
• диапазон изменения значений управляющей переменной (параметра цикла) и одновременно число повторений оператора, содержащегося в теле цикла;
• направление изменения значения параметра цикла (возрастание — to или убывание—downto).
Пример использования оператора for:
for I := 1 to 100 do Read ( M [ I ]); {Чтение элементов массива}
for I:= 100 downto 1 do Write(M[I]); { Вывод элементов массива }
При первом обращении к оператору for вначале вычисляются выражения S1, S2 и осуществляется присваивание <параметр цикла>:= S 1.
После этого циклически повторяются следующие действия:
1. Проверяется условие <параметр цикла>: <= S 2.
2. Если условие выполнено, то оператор for продолжает работу (выполняется оператор в теле цикла), если условие <параметр цикла>:<= S 2 не выполнено, то оператор for завершает работу, и управление в программе передается на оператор, следующий за циклом.
3. Значение управляющей переменной изменяется на +1 (в случае to) или –1 (в случае downto).
Шаг изменения управляющей переменной - единица.
Ограничения использования параметра цикла в операторе for. На использование управляющей переменной (параметра цикла) в цикле for налагаются следующие ограничения:
1. В качестве параметра должна использоваться простая переменная, описанная в текущем блоке.
2. Управляющая переменная должна иметь дискретный тип.
3. Начальные и конечные значения диапазона должны иметь тип, совместимый с типом управляющей переменной. При этом допустим любой скалярный тип, кроме вещественного.
4. В теле цикла запрещается явное изменение значения управляющей переменной (например, оператором присваивания).
5. После завершения оператора значение управляющей переменной становится неопределенным, если только выполнение оператора не было прервано оператором
перехода.
Примеры программ с использованием оператора for
Программа DemoFor1 выводит на экран таблицу перевода из градусов по шкале Цельсия(С) в градусы по Фаренгейту(Р) для значений от 15°С до 30°С с шагом 1 градус. Перевод осуществляется по формуле: F = С*1.8+32.
program DemoFor1;
var
I: integer;
F: real;
begin
Writeln (' Температура ') ;
for I:= 15 to 30 do {Заголовок цикла с параметром}
begin {Начало тела цикла}
F:= I*1.8+32;
Writeln('no Цельсию= ',I,' по Фаренгейту= ', F:5:2)
end; {Конец тела цикла}
end.
В блоке описания переменных описаны параметр цикла I типа integer и переменная F — температура по Фаренгейту типа real. Переменная I, помимо функций управляющей переменной, является переменной, хранящей целочисленные значения температуры по шкале Цельсия. В начале выполнения программы на экран выводится надпись ' Температура ', а затем оператором повтора выводится таблица соотношения температуры в шкалах Цельсия и Фаренгейта. Печать таблицы выполняется оператором Write l n('По Цельсию= ',I,' по Фаренгейту= ' , F: 5:2).
Цикл выполняется следующим образом.
При первом обращении к оператору for вычисляются значения начального (15) конечного (30) параметров цикла, и управляющей переменной I присваивается начальное значение 15.
Затем циклически выполняется следующее:
1. Проверяется условие I <=30.
2. Если оно соблюдается, то выполняется составной оператор в теле цикла, т.е. рассчитывается значение выражения I* 1.8+32, затем оно присваивается переменной F, и на экран выводится сообщение: 'По Цельсию= ', I, ' по Фаренгейту= ', F:5:2.
Если условие I <=30 не соблюдается, т. е. как только I станет > 30, оператор тела цикла не выполняется, а управление в программе передается за пределы оператора for, в нашем примере на оператор end. Программа завершает работу.
3. Значение параметра цикла I увеличивается на единицу, и управление передается в заголовок цикла for для проверки условия.
Далее цикл повторяется, начиная с пункта 1.
Вторым примером оператора цикла for может служить программа DemoFor 2, которая печатает на экране символы американскою стандартного кода обмена информацией (ASCII) в порядке убывания кода.
program DemoFor2;
var
A: integer;
begin
for A:= 255 downto 0 do {Цикл с убыванием параметра }
Writeln('код символа = ',А, ' символ == ',Chr(A));
end.
В данной программе применяется цикл for с убыванием значения управляющей переменной А (используется указание downto - убывание).
Оператор повтора Repeat
Оператор повтора repeat имеет две особенности:
1. Условие проверяется после очередного выполнения операторов тела цикла (очередной итерации) и таким образом гарантируется хотя бы однократное выполнение цикла.
2. Критерием прекращения цикла является равенство выражения константе True.
За это цикл repeat часто называют циклом с постусловием, или циклом "ДО", так как он прекращает выполняться, как только значение выражения условия, записанного после слова until, равно True (истина).
Оператор повтора repeat состоит из заголовка repeat, тела и условия окончания until.
Формат записи:
repeat
<оператор;>
…
<оператор>
until <условие окончания цикла>;
Операторы, заключенные между словами repeat и until, являются телом цикла. Вначале выполняется тело цикла, затем проверяется условие выхода из цикла. Именно поэтому цикл, организованный с помощью оператора repeat, в любом случае выполнится хотя бы один раз. Если результат булевского выражения равен False, то тело цикла активизируется еще раз; если результат True, происходит выход из цикла.
При программировании операторов тела цикла следует обеспечить влияние, по крайней мере, одного из операторов тела цикла на значение условия, иначе цикл будет выполняться бесконечно.
Пример программы с использованием оператора repeat
Примером действия оператора repeat может служить программа DemoRepeat, которая вводит и суммирует любое количество целочисленных значений. Если введено значение 999, то на экран выводится результат суммирования.
program DemoRepeat;
var
X: integer;
Sum; real;
begin
Sum:=0;
repeat { Повторять }
Write('Значение X= '); { Начало тела цикла }
Readln(X); {Считать очередное значение Х с клавиатуры}
if X <> 999 then
Sum:= Sum+X ;
until X = 999; {Условие окончания цикла (пока Х не станет равным 999)}
Writeln('Сумма введенных чисел= ',Sum) ;
end.
В данном примере в разделе описания переменных описана переменная Х целочисленного типа integer и Sum вещественного типа real.
В начале выполнения программы обнуляется значение суммы чисел. Затем зарезервированным словом repeat объявляется цикл, после чего следуют операторы тела цикла, которые выводят на экран запрос 'Значение Х= ', считывают введенное с клавиатуры значение X. Оператор if проверяет его на неравенство числу 999 и, если оно не равно 999, увеличивает значение суммы Sum на значение числа X. В конце цикла оператор until X = 999 проверяет условие окончания цикла. Если значение выражения Х = 999 истинно, то цикл завершится, а управление в программе будет передано на оператор, находящийся за словом until, т. е. первый оператор за границей цикла repeat. Это вызов процедуры Write l n, которая выведет сообщение 'Сумма введенных чисел равна' и напечатает значение переменной Sum.
Оператор повтора while
Оператор while (пока) часто называют оператором цикла с предусловием за то, что проверка условия выполнения тела цикла производится в самом начале оператора.
Формат записи:
while <условие продолжения повторений> do
<тело цикла>;
Условие - булевское выражение, тело цикла - простой или составной оператор.
Перед каждым выполнением тела цикла вычисляется значение выражения условия. Если результат равен True, тело цикла выполняется и снова вычисляется выражение условия. Если результат равен False, происходят выход из цикла и переход к первому после while оператору.
Пример программы с использованием оператора повтора while
Программа DemoWhile производит суммирование 10 произвольно введенных целых чисел.
program DemoWhile;
const
Limit =10; {Ограничение на количество вводимых чисел}
var Count, Item, Sum: integer;
begin
Count:=0; { Счетчик чисел }
Sum:= 0; { Сумма чисел }
while (Count < Limit) do { Условие выполнения цикла }
begin
Count:= Count+1;
Write('Введите ', Count, ' - e целое число: ');
Readln(Item);{Ввод очередного числа с клавиатуры}
Sum:= Sum+Item;
end;
Writeln('Сумма введенных чисел равна ', Sum) ;
end.
В данном примере в разделе описания констант описана константа Limit=10, задающая ограничение на количество вводимых чисел. В разделе описания переменных описаны переменные Count, Item, Sum целочисленного типа. В начале выполнения программы обнуляются значения счетчика введенных чисел Count и их суммы Sum. Затем выполняются цикл ввода 10 чисел и их суммирование. Вначале оператор условия while проверяет условие Count < Limit. Если условие верно, то выполняется составной оператор в теле цикла:
begin
Count:= Count+1;
Write('Введите ', Count, '-e целое число: ');
Readln(Item) ;
Sum:= Sum+Item;
End;
в котором вводится значение очередного числа, и на это значение увеличивается значение суммы. После этого управление в программе вновь передается оператору цикла while, опять проверяется условие Count < Limit. Если условие верно, то выполняется составной оператор и т. д., пока значение переменной Count будет меньше 10. Как только значение Count станет равно 10 и условие Count < Limit не будет соблюдено, выполнение цикла завершится, а управление в программе будет передано на оператор, находящийся за словом end, т. e. первый оператор за границей while. Это вызов процедуры Write l n, которая выведет сообщение 'Сумма введенных чисел равна' и напечатает значение переменной Sum.
Задание 1
Составьте программу для решения одной из следующих задач:
1.1. Для данного натурального числа проверить, делится ли оно на числа: 2, 3, 5, 6, 9.
1.2. По введенному номеру группы выдать сообщение: на каком факультете и на каком курсе учится студент.
1.3. Пройдет ли кирпич со сторонами а, b и с сквозь прямоугольное отверстие со сторонами r и s? Стороны отверстия должны быть параллельны граням кирпича.
1.4. Может ли шар радиуса r пройти через ромбообразное отверстие с диагоналями p и q?
1.5. Можно ли коробку размером a´b´c упаковать в посылку размером r´s´t? «Углом» укладывать нельзя.
1.6. Можно ли на прямоугольном участке застройки размером a´b разместить два дома размерами p´q и r´s метров? Дома можно располагать только параллельно сторонам участка.
Задание 2
Составьте программу для решения одной из следующих задач. Программу запишите на диск под своей фамилией.
2.1. Решить невырожденное (т.е. а¹0) биквадратное уравнение ax4+bx2+c=0.
2.2. Решить невырожденное (т.е. а¹0) квадратное неравенство ax2+bx+c>0.
2.3. Дано натуральное число (n£100), определяющее возраст человека (в годах). Дать для этого числа наименования ”год", ”года", ”лет".
2.4. Дано время (часы, минуты, секунды)-три натуральных числа. Определить время через 10 секунд.
2.5. Определить дату следующего дня. Например:
| 31.12.1985 01.01.1986 29.04.1985 30.04.1985 |
2.6. Определить, каким днем недели является дата, заданная в виде число, месяц (в текущем году).
2.7. Определить число полных лет на текущий момент по введенной с клавиатуры дате.
2.8. По введенной дате рождения определить, является ли на сегодняшний день совершеннолетним пользователь программы.
2.9. Даны целые числа m, n (0<m£12, 0£n<60), указывающие момент времени: ” m часов, n минут". Определить наименьшее время (число полных минут), которое должно пройти до того момента, когда часовая и минутная стрелки на циферблате:
1)совпадут;
2)расположатся перпендикулярно друг другу.
2.10. Определить число полных лет, месяцев и дней на текущий момент по введенной с клавиатуры дате.
Задание 3
Составьте программу, которая рисует во всю высоту экрана один из ваших инициалов, используя введенный символ (букву согласуйте с преподавателем).
Задание 4
Вызовите с диска программу, составленную Вами в задании 2, и добавьте в нее защиту от ввода некорректных данных, т.е. при вводе данных организуйте цикл до тех пор, пока не будут выполнены ограничения, накладываемые на значения аргументов.
Лабораторная работа № 5
Одномерные массивы
Цель работы: Сформировать понятие одномерного массива числового типа. Овладеть умениями обращения к элементам одномерного массива, ввода и вывода массива, составления алгоритмов обработки массивов.
Теоретические сведения
Массивы. Описание массивов
Рассмотренные ранее простые типы данных определяют различные множества атомарных (неразделимых) значений. В отличие от них структурные типы данных задают множества сложных значений, каждое из которых образует совокупность нескольких значений другого типа. В структурных типах выделяют регулярный тип (массивы).
С понятием "массив" приходится сталкиваться при решении научно-технических и экономических задач обработки совокупностей большого количества значений. В общем случае массив - это структурированный тип данных, состоящий из фиксированного числа элементов, имеющих один и тот же тип.
Название регулярный тип (или ряды) массивы получили за то, что в них объединены однотипные (логически однородные) элементы, упорядоченные по индексам, определяющим положение каждого элемента в массиве.
В качестве элементов массива можно использовать и любой другой ранее описанный тип, поэтому вполне правомерно существование массивов записей, массивов указателей, массивов строк, массивов и т.д. Элементами массива могут быть данные любого типа, включая структурированные. Тип элементов массива называется базовым. Особенностью языка Паскаль является то, что число элементов массива фиксируется при описании и в процессе выполнения программы не меняется.
Элементы, образующие массив, упорядочены таким образом, что каждому элементу соответствует совокупность номеров (индексов), определяющих его местоположение в общей последовательности. Доступ к каждому отдельному элементу осуществляется путем индексирования элементов массива. Индексы представляют собой выражения любого скалярного типа, кроме вещественного. Тип индекса определяет границы изменения значений индекса. Для описания массива предназначено словосочетание: array of (массив из).
Формат записи массивов:
Type
<имя типа> = array [тип индекса] of <тип компонента>;
Var
<идентификатор,..> : <имя типа>;
Массив может быть описан и без представления типа в разделе описания типов данных:
V ar
<идентификатор,...> : array [тип индекса] of <тип компонента>;
Примеры описания одномерных и двумерных массивов
Если в описании массива задан один индекс, массив называется одномерным, если два индекса - двумерным, если n индексов — n -мерным массивом. Одномерный массив соответствует понятию линейной таблицы (вектора), двумерный - понятию прямоугольной таблицы (матрицы, набору векторов). Размерность ограничена только объемом памяти конкретного компьютера.
Одномерные массивы обычно используются для представления векторов, а двумерные- для представления матриц.
Одномерные массивы:
Type
Klass = (К1, К2, КЗ, К4) ;
Znak = array [1..255] of char;
Var
Ml: Znak; {Тип Znak предварительно описан в разделе типов}
М2: array[1..60] of integer; {Прямое описание массива М2}
МЗ: array[1..4] of Klass;
Mas: array[1..4] of integer;
Если в качестве базового типа взят другой массив, образуется структура, которую принято называть многомерным массивом.
Двумерные массивы :
Type
Vector = array[1..4] of integer;
Massiv = array[1..4] of Vector;
Var
Matrix : Massiv;
Ту же структуру можно получить, используя другую форму записи:
Var
Matrix : array[1..4,1..4] of integer ;
Для описания массива можно использовать предварительно определенные константы:
Const
G1 = 4; G2 = 6;
Var
MasY: array[1..Gl, l..G2] of real;
Элементы массива располагаются в памяти последовательно. Элементы с меньшими значениями индекса хранятся в более низких адресах памяти. Многомерные массивы располагаются таким образом, что самый правый индекс возрастает самым первым.
Например, если имеется массив:
A:array[1..5,1..5] of integer;
то в памяти элементы массива будут размещены по возрастанию адресов:
А[1,1] А[1,2] … А[1,5] А[2,1] А[2,2] … А[5,5]
Контроль правильности значений индексов массива может проводиться с помощью директивы компилятора R. По умолчанию директива R находится в пассивном состоянии {$R-}. Перевод в активное состояние вызывает проверку всех индексных выражений на соответствие их значений диапазону типа индекса.
Существует различие между регулярными типами в языке Паскаль и массивами в некоторых других языках программирования, заключающееся в том, что в Паскале количество элементов массива всегда должно быть фиксировано, т. е. определяться при трансляции программы. Это считается недостатком языка, так как не во всех программах можно заранее предсказать необходимый размер массива (который может определяться в зависимости от тех или иных условий, возникающих в процессе исполнения). В программах, обрабатывающих массивы, помимо использования для определения размера массива предварительно определенных констант иногда используется прием, позволяющий имитировать работу с массивами переменной длины, который заключается в следующем: в разделе описания констант предварительно определяют возможное максимальное значение размера массива, а затем в программе запрашивают текущее значение размера и используют это значение далее при заполнении и обработке массива.
Действия над массивами
Для работы с массивом как единым целым используется идентификатор массива без указания индекса в квадратных скобках. Массив может участвовать только в операциях отношения "равно", "не равно" и в операторе присваивания. Массивы, участвующие в этих действиях, должны быть идентичны по структуре, т. е. иметь одинаковые типы индексов и одинаковые типы компонентов.
Например, если массивы А и В описаны как
Var
А , В ; array[1..20] of real;
то применение к ним допустимых операций даст следующий результат:
Выражение Результат
А=В True, если значение каждого элемента массива А равно соответствующему значению элемента массива В
А<>В True, если хотя бы одно значение элемента массива А не равно значению соответствующего элемента массива В
А:=В Все значения элементов массива В присваиваются соответствующим элементам массива А. Значения элементов массива В остаются неизменны.
Пример программы ввода-вывода одномерного массива
program priimer1;
uses crt;
var
mas:array [1..10] of integer; {Описание одномерного массива с именем mas , состоящего из 10 элементов типа integer }
n,i:integer; { n -количество элементов массива, i -счетчик в цикле for }
BEGIN
clrscr;
writeln('Введите количество элементов массива не больше 10: ');
readln(n);
for i:=1 to n do {ввод элементов массива}
begin
writeln('Введите ',i,' элемент массива');
readln(mas[i]);
end; { конец ввода }
writeln('Введенный массив: ');
for i:=1 to n do {вывод элементов массива}
begin
write(' ',mas[i],' ');
end; { конец вывода }
readkey;
END.
Пример программы ввода-вывода двумерного массива
program primer2;
uses crt;
var
i,j,n,m:integer;
massiv:array[1..10,1..10] of integer; { описан двумерный массив с именем massiv}
BEGiN
clrscr;
write('Введите количество строк массива (не больше 10): ');
read(n); { n -количество строк}
write('Введите количество столбцов массива (не больше 10):');
read(m); { m -количество столбцов}
for i:=1 to n do {ввод элементов двумерного массива}
begin
for j:=1 to m do
read(massiv[i,j]);
end; { конец ввода }
writeln('Введенный массив: ');
for i:=1 to n do {вывод элементов двумерного массива}
begin
for j:=1 to m do
write(massiv[i,j]:5);
end; { конец вывода }
readkey;
END.
Задание 1
Составьте программу, которая запрашивает значение элементов одномерного числового массива А, формирует и выводит на экран в строку новый числовой массив В, в котором:
1.1. элементы те же, что и в А, но расположены в обратном порядке.
1.2. элементы равны модулю соответствующих элементов А.
1.3. элементы на 1 больше, чем соответствующие элементы А.
1.4. элементы те же, что и в А, но отрицательные заменяются на 0.
Составьте программу для решения одной из следующих задач.
1.5 Подсчета суммы элементов массива, меньших своего номера.
1.6 Подсчета суммы элементов массива, стоящих на четных местах.
1.7 Замены всех элементов массива соответствующими степенями числа 2.
1.8 Замены ненулевых элементов массива на обратные.
Задание 2
Измените предыдущую программу так, чтобы в массиве В, элемент с номером i был равен:
2.1. сумме первых i элементов массива А.
2.2. произведению первых i элементов массива А.
2.3. количеству нулей среди первых i элементов массива А.
2.4. максимальному среди первых i элементов массива А.
2.5. количеству положительных чисел первых i элементов массива А.
2.6. минимальному среди первых i элементов массива А.
2.7. номеру максимального элемента среди первых i элементов А.
2.8. номеру минимального элемента среди первых i элементов А.
После исполнения программы элементы массива В должны быть напечатаны на экране каждый под соответствующим элементом массива А.
Задание 3
Составьте программу для решения одной из следующих задач.
3.1. Определить, есть ли в массиве положительные числа, отрицательные числа, нули.
3.2. Определить, все ли числа из массива А лежат в указанном диапазоне.
3.3. Определить, есть в массиве числа, превосходящие сумму всех элементов массива.
3.4. Определить, единственный ли в массиве максимальный элемент.
3.5. Определить, является ли массив А упорядоченным по возрастанию.
3.6. Определить, является ли массив А упорядоченным по убыванию.
3.7. Определить номер первого нуля в массиве А или выдать сообщение, что нулей в массиве нет.
3.8. Определить, симметричны ли элементы в массиве относительно центрального или центральных.
Задание 4
Составьте программу для решения одной из следующих задач.
4.1. Удалить из массива минимальный элемент
4.2. Подсчитать количество рабочих в данной бригаде, работающих хуже, чем в среднем вся бригада.
4.3. Обменять значениями максимальный и минимальный элементы.
4.4. Подсчитать количество дней, имеющих наибольшую температуру за последнюю декаду марта.
4.5. Найти количество максимальных элементов массива, используя только один оператор цикла.
4.6. Вычислить произведение элементов массива А до первого отрицательного элемента (при наличии отрицательного элемента).
4.7. Вычислить произведение элементов массива А, находящихся между первым максимальным и первым минимальным элементами.
4.8. Вычислить сумму положительных элементов массива А после первого нуля (при наличии нуля).
4.9. Вычислить сумму отрицательных элементов (если такие есть) массива А до первого максимального элемента.
Задание 5
Составьте программу для решения одной из следующих задач.
5.1. Найти второй по величине элемента массива.
5.2. Упорядочить массив А по возрастанию.
5.3. Найти наибольшее количество одинаковых элементов массива А, идущих подряд.
5.4. Подсчитать K- количество элементов, равных первому отрицательному, используя один оператор цикла; если отрицательных нет, то K=-1.
5.5. Исключить нули со сдвигом элементов таблицы.
5.6. По двоичной записи натурального числа M (в виде массива 0 и 1) выдать двоичную запись числа M+1.
5.7. Определить количество разных элементов массива А.
5.8. Найти максимальный из отрицательных элементов массива А с четными номерами (с учетом того, что их может не быть).
5.9. Найти минимальный из положительных элементов массива А с четными номерами (с учетом того, что их может не быть).
5.10. Определить наибольшее количество одинаковых элементов в данном массиве.
Лабораторная работа №6
Теоретические сведения
Строка — это последовательность символов кодовой таблицы персонального компьютера. При использовании в выражениях строка заключается в апострофы. Количество символов в строке (длина строки) может динамически изменяться от 0 до 255. Для определения данных строкового типа используется идентификатор String, за которым следует заключенное в квадратные скобки значение максимально допустимой длины строки данного типа. Если это значение не указывается, то по умолчанию длина строки равна 255 байт.
Переменную строкового типа можно определить через описание типа в разделе определения типов или непосредственно в разделе описания переменных. Строковые данные могут использоваться в программе также в качестве констант.
Недопустимо применение строковых переменных в качестве селектора в операторе Case .
Определение строкового типа устанавливает максимальное количество символов, которое может содержать строка.
Задание 1
Составьте программу для решения одной из следующих задач.
1.1. Определить, какое из двух слов длиннее и на сколько.
1.2. Определить, является ли какое-нибудь из двух слов частью другого.
1.3. Определить, есть ли в записи квадрата данного числа цифра 1.
1.4. Поменять в слове первую и последнюю буквы.
1.5. Если в слове нечетное число букв, то удвоить среднюю.
1.6. По последнему символу определить тип предложения (повествовательное, вопросительное, восклицательное).
1.7. Определить, является ли данный символ латинской буквой.
1.8. Удалить из слова среднюю букву (или две средних).
Задание 2
Составьте программу для решения одной из следующих задач.
2.1. Заменить в арифметическом выражении знаки "+" на знаки "-", а знаки "-" на знаки "+".
2.2. Удалить все буквы "я" в данном слове.
2.3. Удвоить все четные буквы слова.
2.4. Удалить все предлоги "на" в данном предложении.
2.5. Вставить после каждой буквы данного слова букву "о".
2.6. Удалить лишние пробелы в данном предложении.
2.7. Удвоить каждую букву данного слова.
2.8. Заменить каждую точку многоточием (т.е. тремя точками).
Программузапишитена диск.
Задание 3
Вызовите программу, составленную Вами при выполнении задания 2, и переделайте ее так, чтобы в ней использовалась только одна строковая переменная.
Задание 4
Составьте и исполните программу для решения одной из задач.
4.1 Заменить в тексте все маленькие латинские буквы на большие.
4.2 Заменить в тексте все большие латинские буквы на маленькие.
Задание 5
Составьте и исполните программу для решения следующей задачи.
5.1. Удвоить все согласные буквы.
5.2. Удалить из данного слова все согласные буквы.
5.3. Проверить, имеются ли в данном слове одинаковые буквы.
5.4. Оставить в данном слове из каждого набора одинаковых букв, идущих подряд, только одну букву.
5.5. Определить возможность составления одного данного слова из букв другого данного слова с учетом кратности.
5.6. Определить возможность составления одного данного слова из букв другого данного слова без учета кратности.
5.7. Для подсчета количества слов в предложении, учитывая что между словами может быть несколько пробелов.
5.8. Выяснить, можно ли из символов заданного слова составить слово "море".
Лабораторная работа №7
Программирование с использованием процедур и функций[С1]
Цель работы: познакомиться с понятиями "процедура" и "функция" в языке программирования Pascal, рассмотреть их сходства и различия, закрепить практические навыки работы Pascal на примере реализации алгоритмов при помощи процедур и функций, научиться применять метод последовательной детализации в практическом программировании; применять процедуры и функции при решении задач.
Теоретические сведения
Функции
Функция, определенная пользователем, состоит из заголовка и тела функции.
Заголовок содержит зарезервированное слово function, идентификатор (имя) функции, заключенный в круглые скобки необязательный список формальных параметров и тип возвращаемого функцией значения. Тело функции представляет собой локальный блок, по структуре аналогичный программе. В целом структура функции, определенной пользователем имеет вид:
function <имя> (Формальные параметры) : <тип результата>;
const ...
type ...
var
begin
< операторы >
end ;
В разделе операторов должен находиться, по крайней мере, один оператор, присваивающий имени функции значение. В точку вызова возвращается результат последнего присваивания.
Обращение к функции осуществляется по имени с необязательным указанием списка аргументов. Каждый аргумент должен соответствовать формальным параметрам, указанным в заголовке, и иметь тот же тип.
Пример программы с использованием функции, определенной пользователем
Пусть требуется разработать программу вычисления выражения:
Z=(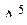 
+ 
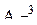)/2* 
,
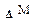в которой возведение в степень выполняется функцией Step.
program DemoFunc;
Var
М : integer;
А,Z,R : real ;
{Функция вычисления степени. N - степень, X – число, возводимое в данную степень. N, X — формальные параметры; результат, возвращаемый функцией в точку вызова, имеет вещественный тип}
function Step(N : integer; X : real): real;
Var
I : integer;
Y : real;
begin
Y:=1;
for I:=1 to N do{ Цикл вычисления N— й степени числа X)
Y:=Y*X;
Step:=Y ; {Присваивание функции результата вычисления степени}
end; {Конец функции}
Begin {Начало основной программы}
Write('Введите значение числа А и показатель степени М');
Readln(A,M) ;
Z:=Step(5,А) ; {Вызов функции с передачей ей фактических параметров N =5, X =А}
Z:=Z+ Step(3,l/A); {Вызов функции с передачей ей фактических параметров N =3, X =1/А}
if M=0 then R:=l {если число возводится в нулевую степень, то результат всегда равен 1}
else if M>0 then R:=Step(M,A){Вызов функции Step с передачей ей фактических параметров М, А}
else R:=Step(-M,A); {Вызов функции с передачей ей фактических параметров: - М, отрицательная степень}
Z:=Z/(2*R) ;
Writeln(' Для А= ',А,'М= ',М,' Значение выражения= ',Z);
end.
В начале программы описываются переменная целого типа М и переменные вещественного типа А, Z, R, после этого описывается функция вычисления степени числа Step с формальными параметрами N и X, результат, возвращаемый функцией в точку вызова, - вещественного типа.
В описании функции вводятся две локальных (местных) переменных I и Y. Переменная I служит для подсчета числа повторений цикла, а в Y накапливается значение степени как произведения N одинаковых сомножителей. В заключение функции присваивается значение вычисленного произведения.
В начале выполнения основной программы на экран выводится запрос "Введите значение числа А и показатель степени М" и считывается с клавиатуры значение вещественного числа А и целого числа М.
Затем выполняется оператор:
Z := Step (5, A );
Осуществляется вызов функции Step с передачей ей фактических параметров 5, А. Их значения присваиваются формальным параметрам функции N и X. По окончании вычисления степени числа значение функции Step, вычисленное для фактических параметров 5 и А, присваивается переменной Z. Аналогично в операторе:
Z := Z + Step (3, l / A );
сначала осуществляется вызов функции Step с передачей ей фактических параметров 3, 1/A, после чего значение переменной Z увеличивается на величину возвращенного в основную программу результата вычисления функции Step.
Операторы:
if M=0 then R:=1
else if M>0 then R:=Step(M,A)
else R:=Step(- M,A);
проверяют условия М=0, М>0 и в зависимости от их соблюдения либо присваивает переменной R значение 1 (при М=О), либо выполняет вызов функции Step для фактических значений М, А или -М, А, а после вычисления значения функции Step присваивает его переменной R.
Оператор:
Z := Z /(2* R );
выполняет вычисление значения выражения, а затем присваивает вычисленное значение переменной Z.
В заключение программы стандартная процедура Write l n выводит на экран сообщение о результате вычислений степени М числа А.
Процедура
Описание процедуры включает заголовок (имя) и тело процедуры. Заголовок состоит из зарезервированного слова procedure, идентификатора (имени) процедуры и необязательного, заключенного в круглые скобки, списка формальных параметров с указанием типа каждого параметра. Имя процедуры — идентификатор, уникальный в пределах программы. Тело процедуры представляет собой локальный блок, по структуре аналогичный программе.
Описания меток, констант, типов и т. д. действительны только в пределах данной процедуры. В теле процедуры можно использовать любые глобальные константы и переменные. Общая структура описания процедур:
procedure <имя> (Формальные параметры);
const ... ;
type . . . ;
var . . . ;
begin
<операторы>
end ;
Пример программы с использованием процедуры, определенной пользователем
В качестве примера опишем процедуру, которая прерывает выполнение программы и выдает соответствующее сообщение об ошибке.
procedure Abort(Msg: string);
begin
Writeln(' Ошибка : ', Msg);
Halt (1);
end ;
В данной процедуре пользователя использована переменная Msg типа string, в которой хранится текст сообщения о характере ошибки, вызвавшей прерывание программы. Для прерывания выполнения программы используется стандартная процедура Halt из стандартного библиотечного модуля System.
Процедура не может выполниться сама, ее необходимо вызвать по имени и указать фактические параметры того же типа, что и формальные. Количество и тип формальных параметров равны количеству и типу фактических параметров.
В качестве примера приведем фрагмент программы, в котором используется описанная выше процедура Abort.
program DemoProc; {Подсчет суммы десяти введенных целых положительных чисел: если будет введено отрицательное число, прервать выполнение}
const
Limit= 10; {Ограничение на количество вводимых чисел)
var
Count, Item, Sum : integer;
procedure Abort(Msg: string); { описание и реализация процедуры Abort}
begin
Writeln('Ошибка: ', Msg);
Halt(1);
end ;
Begin {основная программа}
Count:= 0;
Sum: = 0 ;
while (Count < Limit) do { Условие выполнение цикла }
begin
Count:= Count+1;
Write('Введите ', Count, '-e целое число: ');
Readln(Item);
if Item < 0 then { Если введено отрицательное число }
Abort('Введено отрицательное число! '); {Вызов процедуры}
Sum:= Sum+Item;
end;
Writeln('Сумма введенных чисел равна ', Sum);
end.
В разделе описания программы описываются константа Limit, ограничивающая количество вводимых чисел; в разделе описания переменных описываются переменные Count, Item, Sum типа integer.
В начале программы обнуляются значения количества введенных чисел Count и их сумма Sum. Потом выполняется цикл, пока очередное вводимое число меньше предельного, заданного значением константы Limit. Сначала устанавливается номер очередного числа, затем на экран выводится приглашение "Введите 1-е (2-е и т.п.) число", считывается значение числа с клавиатуры в переменную Item. Затем проверяется условие Item<0.
Если условие выполняется, то вызывается Abort, которой передается фактический параметр-значение типа string: "введено отрицательное число". Это значение присваивается формальному параметру Msg процедуры Abort. Процедура Abort выводит на экран сообщение об ошибке и печатает текст сообщения - значение параметра Msg: "Ошибка: введено отрицательное число", после чего вызывает стандартную процедуру Halt(1), которая прерывает выполнение программы.
Если условие Item<0 не выполняется, то значение суммы Sum увеличивается на значение введенного числа Item, и управление передается в заголовок цикла для проверки условия Count < Limit. Если условие соблюдается, то тело цикла выполняется еще раз, иначе цикл завершается, а управление в программе передается на оператор, следующий за циклом, т. е. за резервированным словом end, обозначающим окончание составного оператора в теле цикла. После этого на экран выводится сообщение: "Сумма введенных чисел равна" и печатается значение переменной Sum. На этом выполнение программы завершается.
Механизм передачи параметров
Как было показано в приведенных выше примерах программ с использованием процедур и функций, в заголовке процедуры или функции может быть задан список параметров, которые называются формальными. Название "формальные" эти параметры получили в связи с тем, что в этом списке заданы только имена для обозначения исходных данных и результатов работы процедуры, а при вызове подпрограммы на их место будут подставлены конкретные значения (выражений) и имен. Этот список указывается после имени подпрограммы и заключается в круглые скобки.
В списке формальных параметров должны быть перечислены имена формальных параметров и их типы. Имя параметра отделяется от типа двоеточием, а параметры друг от друга - точкой с запятой. Имена параметров одного типа можно объединять в подсписки, в которых имена отделяются друг от друга запятой.
Между формальными и фактическими параметрами должно быть полное соответствие:
• формальных и фактических параметров должно быть одинаковое количество
• порядок следования фактических и формальных параметров должен быть один и тот же;
• тип каждого фактического параметра должен совпадать с типом соответствующего формального параметра.
Параметры-значения.
Параметры-значения используются только для передачи исходных данных из основной программы в подпрограмму (процедуру или функцию), в списке формальных параметров они перечисляются через запятую с обязательным указанием их типов, как было, например, в выше приведенных примерах:
procedure Abort(Msg: string);
function Step(N : integer; X : real): real;
Если формальный параметр объявлен как параметр-значение, то фактическим параметром может быть произвольное выражение. При вызове подпрограммы фактические параметры вычисляются и используются как начальные значения формальных параметров, т. е. осуществляется подстановка значений. Если формальный параметр определен как параметр-значение, то перед вызовом процедуры это значение вычисляется, полученный результат помещается во временную память и передается процедуре. Даже если фактический параметр - простейшее выражение в виде константы или переменной, все равно процедуре будет передана лишь копия этой константы (переменной). В процессе выполнения подпрограммы формальные параметры могут изменяться, но это никак не отразится на соответствующих фактических параметрах-переменных, которые сохранят те значения, которые имели до вызова подпрограммы, так как меняются не они, а их копия. Поэтому параметры-значения нельзя использовать для передачи результатов из подпрограммы в основную программу.
Пример программы с использованием передачи параметров по значению:
program Pr1;
var
А,В : real;
{Процедура вычисления квадратов двух чисел и вывода их суммы}
procedure Sum_Square(X, Y : real); {X,Y - формальные параметры }
begin
Х:=Х*Х;
Y:=Y*Y;
Writeln('Cyммa квадратов = ',X+Y);
end; {Конец процедуры}
begin {Начало основной программы}
А:=1.5;
В:=3.4;
Sum_Square (А,В) ; {Вызов процедуры Sum _ Square с передачей ей значений фактических параметров А и В}
end.
При вызове процедуры Sum_Square с фактическими параметрами А, В значения этих параметров (один раз) копируются в соответствующие формальные параметры X, Y, и дальнейшие преобразования формальных параметров X,Y внутри процедуры Sum_Square уже никак не влияют на значения переменных А, В.
Параметры-переменные
Параметры-переменные используются для определения результатов выполнения процедуры и в списке формальных параметров перечисляются после зарезервированного слова Var с обязательным указанием типа. Каждому формальному параметру, объявленному как параметр-переменная, должен соответствовать фактический параметр в виде переменной соответствующего типа, например:
procedure Example(var M,N : integer; var Y : real) ;
Если формальный параметр определен как параметр-переменная, то при вызове процедуры ей передается сама переменная, а не ее копия, и изменение параметра-переменной приводит к изменению фактического параметра в вызывающей программе. Следовательно, исходные данные в процедуру из программы могут передаваться как через параметры-значения, так и через параметры-переменные, а результаты работы процедуры возвращаются в вызывающую программу только через параметры-переменные.
Пример программы, использующей параметры-переменные:
program Sum_Sub_Square;
var
A,В : real ;
SumAB, SubAB : real;
{Процедура с параметрами-переменными Sum , Sub }
procedure Sum_Sub(X,Y : real; var Sum, Sub : real);
begin
Sum:=X*X+Y*Y;
Sub:=X*X-Y*Y;
end; { Конец процедуры }
begin {Начало основной программы}
А:=1.5;
В:=3.4;
Sum_Sub(A,B, SumAB,SubAB); {Вызов процедуры с передачей ей фактических параметров-значений А, В и параметров-переменных SumAB , SubAB}
Writeln('Сумма квадратов чисел',А,' и ',В,'= ', SumAB);
Writeln("Разность квадратов чисел',А,’и',В,'=', SubAB);
end.
Задания.
1. Даны действительные числа х1, у1, х2, у2, …,х10, у10. Найти периметр десятиугольника, вершины которого имеют соответственно координаты (х1, у1), (х2, у2), …, (х10, у10). (Определить процедуру вычисления расстояния между двумя точками, заданными своими координатами.)
2. Даны действительные числа a, b, c, d, e - стороны пятиугольника. Найти площадь пятиугольника. (Определить процедуру вычисления площади треугольника по его сторонам.)
3. Даны координаты вершин двух треугольников. Определить, какой из них имеет большую площадь.
4. Дано натуральное число n. Выяснить, является ли оно полным квадратом. Определить функцию, позволяющую распознавать полные квадраты.
5. Дан массив A[1..50], элементы которого отличны от нуля. Расположить их в таком порядке, чтобы первыми были все положительные элементы, а затем - все отрицательные, причем порядок следования как положительных, так и отрицательных элементов должен сохраниться (при решении задачи новый массив не заводить!).
6. Составить функцию для нахождения точного значения суммы натуральных чисел, в десятичной записи которых более 20 знаков. Указание. Исходные данные и ответ представить в виде массивов цифр.
7. Рассмотрим произвольное натуральное число и найдем сумму его цифр, затем сумму цифр полученного числа и так далее, пока не получим однозначное число. Назовем это число цифровым корнем. Требуется написать программу, которая для заданного N (N<10100) находит его цифровой корень.
Лабораторная работа №8
Задание 1
Составить и опробовать процедуру, считывающую текстовый файл с именем "sem1.21?", в котором каждая строка представляет собой фамилию студента и список всех оценок по ОИВТ, полученных им за первый семестр. При этом фамилия отделяется от оценок запятой, так же как и оценки друг от друга. Знак "?" в имени файла надо заменить на порядковый номер вашей группы. Для проверки правильности чтения из каждой строки надо выделять фамилию и распечатывать их в столбик.
Задание 2
Дополнить предыдущую процедуру так, чтобы после считывания строки и выделения фамилии остаток строки разбивался на отдельные оценки, из которых создаются следующие числовые массивы:
- оценки за лабораторные работы (по 15 оценок у каждого)
- баллы за самостоятельные работы (по 5 оценок у каждого)
- баллы за собеседования (по 5 оценок у каждого)
- оценки за контролирующие программы (по 9 оценок у каждого)
- балл за итоговую контрольную работу
При этом должны вычисляться итоговые суммы по оценкам, записанным в строке и печататься вместе с фамилией на экран.
Дополнительное задание
Составить и проверить работу процедуры, которая проверяет по полученным массивам корректность выставления оценок и выдает сообщение о том, что все оценки допустимые или полные сообщения о недопустимых оценках. При этом процедура должна производить пересчет неверных оценок. Например, если оценка за лабораторную работу 7 или 10, то ее надо заменить на 5, а оценку -3 за самостоятельную работу надо заменять на оценку -2 и т.д.
Задание 3
Составить процедуру печати информации в виде таблицы.
Задание 4
Составить и проверить работу процедуры, которая создает текстовый файл, в каждой строке которого записана фамилия студента и набранная им за семестр общая сумма баллов, отделенная от фамилии знаком "-".
Задание 5
Дополнить предыдущую программу так, чтобы в файл данные записывались упорядоченными по убыванию суммы набранных студентом за семестр баллов.
Дополнительное задание.
С помощью составленной программы создать два текстовых файла с итогами работы за семестр двух групп вашего потока. Затем составить процедуру, которая из двух отсортированных файлов создает один общий отсортированный файл, где к каждой строке добавлен еще номер группы.
Лабораторная работа №9
Рекурсивные функции
Цель: приобрести навыки работы с рекурсивными алгоритмами, понять отличие рекурсии и итерации.
Теоретические сведения
К функциям можно обращаться тремя способами: из тела основной программы, из тела другой функции, из тела самой функции, т.е. функция может вызывать саму себя. Функции называются рекурсивными, если в описании функции происходит вызов самой себя, а процесс обращения – рекурсией. Продемонстрируем использование рекурсии на примере вычисления значения факториала произвольного натурального числа N.
В математике известно рекурсивное определение факториала:
n! = 1 при n = 0;
n! = (n - 1)! × n при n > 0.
Это рекурсивное определение можно реализовать с помощью соответствующей рекурсивной функции:
function FACTORIAL (VALUE: integer): integer;
begin
iF VALUE = 0 then FACTORIAL := 1
else FACTORIAL := VALUE*FACTORIAL (VALUE - 1)
end;
Теперь можно обращаться к этой функции в теле основной программы, как показано в следующем примере:
program FINDFACTORIAL;
var N: integer;
begin
writeln ('Введите число');
readln (N);
if N < 0 then writeln ('Нет факториала')
else writeln ('Факториал ', N, ' равен ', FACTORIAL (N))
end.
Мы видим, что характерной особенностью построенной функции является наличие в ее теле оператора присваивания:
FACTORIAL := VALUE*FACTORIAL (VALUE - 1),
где происходит вызов определяемой функции. Здесь идентификатор FACTORIAL в левой части оператора обозначает имя переменной для хранения значения функции, а в правой – имя вызываемой функции.
Важным моментом при составлении любой рекурсивной функции является организация выхода из рекурсии. В некоторых простых случаях должно существовать не рекурсивное решение. Рекурсивный процесс должен шаг за шагом так упрощать задачу, чтобы, в конце концов, для нее появилось не рекурсивное решение. В этих функциях должны проверяться значения аргумента для принятия решения о завершении. В нашем случае условием завершения рекурсии является VALUE = 0.
При описании рекурсивных функций необходимо хорошо представлять процесс вычислений. Всякая рекурсия состоит из двух этапов: углубления (погружения) внутрь рекурсии и выхода из нее. На первом этапе никаких вычислений не производится, а идет только настройка рабочей формулы на конкретные операнды. На втором этапе происходит процесс вычислений по настроенным формулам.
В заключение покажем, что часто рекурсивные функции строятся гораздо проще, чем «обычные», хотя вполне понятно, что не всякая функция может быть переделана на рекурсивную. Сделаем это на примере уже построенной ранее функции POWER.
Данная функция явно носит рекурсивный характер, исходя из ее определения:
Xn = 1, если n = 0;
Xn = Xn-1 * X, если n > 1.
Ниже следует рекурсивная функция вычисления значения степени:
function POWER (FACTOR: real; EXPONENT: integer): REAL;
begin
if EXPONENT < 0
then POWER := 1/POWER (FACTOR, abs (EXPONENT))
else
if EXPONENT > 0
then POWER := FACTOR*POWER (FACTOR, EXPONENT - 1)
else POWER := 1
end;
Замечание. Помимо рекурсивных функций, в языке Паскаль по тому же принципу можно определять и рекурсивные процедуры. Подробно о них будет сказано в следующих разделах, а пока покажем, как рекурсивная функция может быть переделана в рекурсивную процедуру на примере вычисления факториала:
procedure FACTORIAL (VALUE: integer; var F: integer);
begin
iF VALUE = 0 then F := 1
else begin FACTORIAL (VALUE - 1, F);
F := F*VALUE
end;
end;
Здесь уже, в отличие от функции FACTORIAL, для вычисления N! необходимо вызвать эту процедуру с помощью оператора процедуры FACTORIAL (N, FN), где FN – переменная для возвращения из процедуры значения N!.
Пример. Создать рекурсивную функцию поиска i-го члена последовательности, заданной рекуррентной формулой A1=const1, A2=const2, Ai=3Ai-2-Ai-1. Вывести через пробел значения рекурсивной функции при значениях аргумента от 1 до 10 включительно.
Решение. По условию задачи аргумент может принимать только целые значения, поэтому функция имеет параметр-значение типа Integer. Выход из рекурсии в данном случае осуществляется при двух значениях аргумента (при i=1, i=2), поэтому в рекурсивной функции необходимы два вложенных условных оператора или же оператор выбора case. В приведенном примере использованы операторы if, но попробуйте самостоятельно записать решение с помощью оператора выбора. В основной программе значения аргумента - целые последовательные числа, поэтому следует воспользоваться оператором цикла с параметром for.
program proc_2;
function A (i: Integer): Integer;
begin
if i=1 then A:=1 else
if i=2 then A:=3 else А:=3*A(i-2)-A(i-1)
end;
var i: Integer;
begin
for i:=1 to 10 do Write (A(i),' ');
Readln
end.
Задание 1.
Вывести значения рекурсивной функции при значениях аргумента от 1 до 10 включительно.
a) Найти член последовательности, заданной формулой: Di =7+ Di -1 при i>1, где D1 определяется пользователем.
b) Найти член последовательности, заданной формулой: Ai = Ai -1 - Ai -2 при i>2. Значения первого и второго членов последовательности вводятся пользователем.
c) Найти член последовательности, заданной следующим образом:
y1=0; y2=10; yn=2×yn-1-yn-2, где n>2.
d) Найти член последовательности, заданной формулой Bi =4· Bi -1, при i>1. Значения первого члена последовательности вводится пользователем.
Задание 2.
Дан квадрат со стороной а, диагональ этого квадрата является стороной второго квадрата, диагональ второго квадрата – стороной третьего и т.д. (вложенность квадратов запрашивается при старте программы). Найти длину стороны последнего квадрата, используя функцию вычисления длины диагонали квадрата по его стороне:
Задание 3.
Реализовать в программе рекурсивную функцию, которая в указанной директории производит следующие действия:
· в текущей директории создаётся папка;
· созданная папка становится новой текущей директорией;
· в новой текущей директории создаются 10 файлов с произвольным содержимым (можно использовать функцию random ).
· Рекурсивный вызов
Функция должна вызывать саму себя до тех пор, пока размер исходной директории не будет больше 1 Мб.
Лабораторная работа №10
Теоретические сведения
Указатели
Оперативная память компьютера может рассматриваться как массив байтов, индексируемый от нуля. Номер каждого байта в этом массиве называется его адресом. Адресом переменной называется адрес ее первого байта. Для получения адреса переменной в языке Pascal используется унарная операция @: @x – адрес переменной x.
Переменные, в которых хранятся адреса, называются указателями. Любой указатель в 32-разрядной операционной системе занимает 4 байта. Это дает возможность адресовать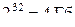 
ячеек памяти. С переходом на 64-битные системы объем адресуемой оперативной памяти станет практически безграничным.
Для чего нужны указатели? Их использование повышает гибкость программирования и разграничивает обязанности: указатель знает лишь адрес переменной, сама переменная может менять свое значение независимо от наличия указателя на нее. Можно провести аналогию между указателями и справочной службой 09. Клиент обращается в справочную службу для того, чтобы узнать номер телефона абонента. Другими словами клиент обращается к указателю, который знает адрес объекта и, следовательно, может вернуть значение этого объекта (в данном случае – номер телефона). Гибкость такого способа очевидна: не следует помнить номера всех телефонов, достаточно знать номер телефона справочной. Кроме того, если номер телефона абонента будет изменен, то в справочной службе будет произведена оперативная корректировка информации, и при последующем обращении в службу клиент получит измененный номер телефона. Другой пример: несколько указателей (банкоматов) указывают на один объект (банковский счет). Посредством разных банкоматов можно снимать деньги с одного банковского счета. Третий пример: файловый указатель, который обращается всякий раз к текущему элементу файла, после чего перемещается на следующий. Это позволяет единым образом (через один указатель) работать с различными данными, находящимися в файле.
В языке Delphi Pascal указатели делятся на типизированные и бестиповые. Если T – некоторый тип, то типизированный указатель на него описываются следующим образом: ^T (указатель на тип). Бестиповой указатель описывается с помощью типа pointer. Если типизированный указатель хранит адрес переменной заданного типа, то бестиповой хранит просто адрес некоторого участка памяти.
Будем изображать тот факт, что указатель pa хранит адрес переменной a, следующим образом:
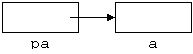
При этом говорят, что pa указывает на a. Указатель может также хранить специальное значение, задаваемое предопределенной константой nil. Это «нулевое значение» для указателей, означающее, что указатель никуда не указывает. Будем называть такой указатель нулевым и изображать его следующим образом:
Типизированные указатели разных типов несовместимы по присваиванию. Однако типизированный и бестиповой указатель совместимы по присваиванию в обе стороны. Указатели одного типа, а также типизированный и бестиповой указатель можно сравнивать на равенство и неравенство. Далее приводятся примеры допустимых действий с указателями:
var a: integer;
r: real;
pa,pa1: ^integer;
p,p1: pointer;
pr: ^real;
Begin
pa:=@a;
p:=@a;
pa:=p;
p:=pa;
p:=nil;
pa:=nil;
if pa=pa1 then ;
if pa<>p then ;
...
Следующие действия, наоборот, являются недопустимыми и вызовут ошибку компиляции, поскольку выполняются над указателями, имеющими различный базовый тип:
pr:=pa; // ошибка: несовместимые типы
if pr=pa then; // ошибка: несовместимые типы
Следует помнить, что в языке Pascal принята именная эквивалентность типов. Поэтому в следующем примере переменные pb и pb1 считаются принадлежащими к разным типам:
var pb: ^integer;
pb1: ^integer;
Begin
pb:=pb1; // ошибка компиляции!
if pb<>pb1 then ; // ошибка компиляции!
...
Чтобы можно было присваивать и сравнивать указатели на один и тот же тип, описанные в разных местах, а также передавать указатели как параметры подпрограмм, следует определить новый тип-указатель и описывать переменные-указатели, используя этот тип:
type pinteger=^integer;
var pb: pinteger;
pb1: pinteger;
procedure pr(p: pinteger);
Begin
...
end;
...
pb:=pb1; // верно
if pb<>pb1 then ; // верно
pr(pb); // верно
К типизированным указателям применима операция разыменовыния ^ : запись pa^ означает «объект, на который указывает pa» (под объектом здесь понимается область памяти, выделенная программой и трактуемая как переменная или константа определенного типа). В частности, если pa хранит адрес переменной a, то разыменованный указатель pa^ и имя переменной a эквивалентны, поскольку ссылаются на один объект. Вообще, ссылка на объект – это выражение, однозначно определяющее этот объект. В нашем примере имя переменной a и выражение pa^ являются ссылками на один и тот же объект в памяти.
Нулевой указатель и указатель типа pointer разыменовывать нельзя. При разыменовании переменной-указателя, имеющей нулевое значение, произойдет ошибка времени выполнения, разыменование же указателя pointer приведет к ошибке компиляции.
Если типизированный указатель хранит адрес записи или массива, то в Delphi Pascal при обращении через указатель к полю записи или элементу массива операцию разыменования можно не использовать. Например:
type IArr = array [1..100] of integer;
Rec = record i,j: real; end;
var a: IArr; pa: ^IArr;
r: Rec; pr: ^Rec;
Begin
pa:=@a;
pr:=@r;
pa[1]:=2; // вместо pa^[1]:=2
pr.i:=3; // вместо pr^.i:=3
end.
Неявные указатели
Указатели неявно встречаются во многих конструкциях языка программирования. Например, при передаче параметра по ссылке в подпрограмму на самом деле передается указатель. Сравним две реализации одной процедуры:
procedure Mult2(var i: integer);
Begin
i:=i*2;
end;
procedure Mult2P(pi: pinteger);
Begin
pi^:=pi^*2;
end;
var a: integer;
Begin
a:=3;
Mult2(a);
Mult2P(@a);
...
Код, генерируемый для таких процедур, практически идентичен: в обоих случаях в процедуру передается адрес переменной, которую следует удвоить. Однако пользоваться первой версией процедуры с параметром, передаваемым по ссылке, гораздо удобнее: в теле процедуры не надо разыменовывать указатель и при вызове процедуры в качестве параметра надо указывать саму переменную, а не ее адрес. Из данного примера видно, что параметр, передаваемый по ссылке, можно трактовать как указатель, который при использовании неявно разыменовывается.
Другой пример неявных указателей – процедурные переменные. Процедурная переменная хранит адрес процедуры или функции с соответствующей сигнатурой, либо же значение nil (напомним, что сигнатура подпрограммы определяется ее заголовком и включает количество и типы ее параметров, а для функций также и тип возвращаемого значения). Для присваивания процедурной переменной a адреса подпрограммы p с соответствующей сигнатурой знак операции @ использовать необязательно: записи a:=@p и a:=p равнозначны. Например:
type proc = procedure (i: integer);
func = function: real;
var a: proc;
b: func;
procedure p(i: integer);
Begin
...
end;
function f: real;
Begin
...
end;
Begin
a:=@p;
b:=f; // равноценно b:=@f
a(5); // вызов процедуры через процедурную переменную a
writeln(b); // вызов функции через процедурную переменную b
end.
Указатели pointer
Бестиповые указатели pointer хранят адрес памяти, не связанный с объектом определенного типа, и не могут быть разыменованы. Чтобы воспользоваться данными по этому адресу, бестиповой указатель следует преобразовать к указателю на конкретный тип. Например:
type pinteger = ^integer;
preal =^real;
var i: integer;
r: real;
p: pointer;
Begin
p:=@i;
pinteger(p)^:=5;
writeln(pinteger(p)^);
p:=@r;
preal(p)^:=3.14;
writeln(preal(p)^);
end.
Рассмотрим запись pinteger(p)^ подробнее. Здесь перед доступом к данным по указателю p мы вначале преобразуем его к указателю на integer, а потом разыменовываем. Поскольку перед обращением к pinteger(p)^ было выполнено присваивание p:=@i, то выражение pinteger(p)^ становится синонимом имени i и может быть использовано как в левой, так и в правой части оператора присваивания.
Гибкость указателей pointer имеет обратную сторону: их применение потенциально опасно и может приводить к ошибкам, причину которых сложно установить. Например, в результате выполнения кода
p:=@i;
preal(p)^:=3.14;
мы обратимся к участку памяти, по которому расположено значение целой переменной i, как к вещественной переменной. Поскольку данные вещественного типа занимают в памяти 8 байт (в Delphi), а данные целого типа – всего 4 байта, то последнее присваивание не только изменит 4 байта, занимаемые переменной i, но и запишет оставшиеся 4 байта в область памяти, следующую за переменной i. Поскольку обычно память под глобальные переменные выделяется подряд в порядке их описания, то оставшиеся 4 байта запишутся в область памяти, отведенную под переменную r (именно она описана вслед за i), то есть в результате последнего присваивания значение переменной r будет испорчено. Подобная ошибка не будет выявлена на стадии компиляции, а при выполнении программы проявится не при данном ошибочном присваивании, а позже, когда мы захотим воспользоваться значением переменной r. Именно поэтому рекомендуется либо отказаться от использования бестиповых указателей, либо при их использовании проявлять предельную аккуратность.
Приведем пример, в котором использование указателей pointer оправдано.
Пример. Внутреннее представление значения real.
Зададимся целью посмотреть, как хранится в памяти переменная типа real. Для этого запишем ее адрес в указатель pointer, после чего преобразуем его в указатель на массив байтов и выведем этот массив на экран.
const sz = sizeof(real);
type Arr=array [1..sz] of byte;
PArr=^Arr;
var r: real;
p: pointer;
pb: PArr;
i: integer;
Begin
readln(r);
p:=@r;
pb:=p;
for i:=1 to sz do
write(pb^[i],’ ’);
end.
Отметим одну особенность операции взятия адреса @. В Delphi ее результат зависит от директивы компиляции {$T} («typed @ operator»). По умолчанию установлена директива компиляции {$T-}: это означает, что результат операции @ имеет тип pointer. Если же установлена директива компиляции {$T+}, то результат операции @ – типизированный указатель, базовым типом для которого выступает тип операнда. Кроме того, можно получить адрес переменной, воспользовавшись стандартной функцией Addr(x), которая всегда возвращает значение типа pointer.
Особенностью операции @ можно воспользоваться, чтобы упростить последнее решение. Для этого поставим в начале программы директиву компиляции {$T-}, что позволит нам заменить присваивания p:=@r; pb:=p на pb:=@r и исключить из программы описание переменной p. Подчеркнем, что в режиме {$T+} последнее присваивание приведет к ошибке несоответствия типов, поскольку @r будет возвращать значение типа ^real. Впрочем, в режиме {$T+} можно воспользоваться явным приведением типов (pb:=PArr(@r)) или функцией Addr (pb:=Addr(r)):
Процедуры New и Delete
Для выделения динамической памяти, контролируемой типизированным указателем, используется стандартная процедура New, для освобождения – стандартная процедура Dispose. Если pt – указатель на тип T, то вызов New(pt) распределяет в динамической памяти переменную типа T и записывает в pt адрес этой переменной:
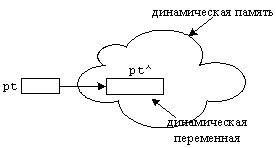
Переменная, распределенная в динамической памяти, называется динамической переменной. Она не имеет своего имени и для доступа к ней используется разыменованный указатель pt^. После работы с динамической переменной занимаемая ею память должна быть освобождена вызовом стандартной процедуры Dispose, например: Dispose(pt). Таким образом, динамическая переменная существует между вызовами New и Dispose:
var pt: ^real;
Begin
New(pt);
pt^:=2.8;
pt^:=pt^*2;
...
Dispose(pt);
end.
Выделение и освобождение динамической памяти выполняется специальной подсистемой программы, называемой менеджером кучи. Менеджер кучи хранит список всех незанятых блоков в динамической памяти. При вызове New менеджер кучи ищет незанятый блок подходящего размера, выделяет в нем память и модифицирует список незанятых блоков. При вызове Dispose блок вновь помечается как свободный. После завершения программы вся выделенная для нее динамическая память автоматически возвращается назад системе.
Если динамическая память выделяется в подпрограмме для решения локальных задач данной подпрограммы, то она должна быть освобождена в конце работы этой подпрограммы. Исключение составляют так называемые «создающие» подпрограммы, основным предназначением которых является вернуть объект, созданный в динамической памяти. Например:
function NewInteger(i: integer): pinteger;
Begin
New(Result);
Result^:=i;
end;
var pi: pinteger;
Begin
pi:= NewInteger(5);
...
При своем вызове функция NewInteger возвращает указатель на динамическую переменную, которая должна быть впоследствии освобождена. Основная проблема состоит в том, что NewInteger не является стандартной функцией, и при ее вызове можно забыть, что она выделяет динамическую память. Один из способов «напомнить» об этом программисту – дать функции имя, свидетельствующее о ее «создающей» способности. Например, имя такой функции может начинаться с префикса New или Create.
Пример. Массив указателей на переменные разных типов.
В некоторых задачах возникает необходимость хранить в массиве данные различных типов. Пусть в массиве требуется хранить данные типа integer, real и shortstring.
Приведем вначале решение, не использубщее указатели.
Решение 1. Используем записи с вариантами. Опишем следующие типы:
type TVar=(tInt,tReal,tStr);
Variant = record
case t: TVar of
tInt: (i: integer);
tReal: (r: real);
tStr: (s: shortstring);
end;
Теперь опишем массив записей Variant и добавим в него несколько значений:
var A: array [1..10] of Variant;
Begin
A[1].t:=tInt; A[1].i:=5;
A[2].t:=tReal; A[2].r:=3.14;
A[3].t:=tStr; A[3].s:='Delphi';
end.
Для вывода содержимого массива, очевидно, следует воспользоваться циклом
for i:=1 to 3 do
case A[i].t of
tInt: writeln(A[i].i);
tReal: writeln(A[i].r);
tStr: writeln(A[i].s);
end;
Такое решение имеет важный недостаток: каждый элемент массива имеет размер, определяемый самым большим типом shortstring, что расточительно.
Решение 2. В вариантной части записи Variant будем хранить не значения соответствующих типов, а указатели на них:
Type
TVar=(tInt,tReal,tStr);
pinteger=^integer;
preal=^integer;
pshortstring=^shortstring;
Variant = record
t: TVar;
case t: TVar of
tInt: (pi: pinteger);
tReal: (pr: preal);
tStr: (ps: pshortstring);
end;
Будем добавлять в такой массив указатели на переменные разных типов:
var A: array [1..10] of Variant;
Begin
A[1].t:=tInt; New(A[1].pi); A[1].pi^:=5;
A[2].t:=tReal; New(A[2].pr); A[2].pr^:=3.14;
A[3].t:=tStr; New(A[3].ps); A[3].ps^:='Delphi';
Для вывода содержимого такого массива воспользуемся следующим циклом:
for i:=1 to 3 do
case A[i].t of
tInt: writeln(pinteger(A[i].p)^);
tReal: writeln(preal(A[i].p)^);
tStr: writeln(pstring(A[i].p)^);
end;
В данном решении суммарный объем данных определяется не размером максимального типа данных, а реальным содержимым в момент выполнения программы. По окончании работы с массивом A динамическую память, занимаемую его элементами, следует освободить. Поскольку параметр процедуры Delete имеет тип pointer, то для освобождения занимаемой памяти можно передать любое из полей-указателей, например, pi:
for i:=1 to 3 do
Delete(A[i].pi);
Процедуры GetMem и FreeMem
Для выделения/освобождения динамической памяти, контролируемой бестиповым указателем, используется другая пара процедур: GetMem и FreeMem. Если p – указатель любого типа (в частности, типа pointer), то вызов GetMem(p,nb) выделяет в динамической памяти участок размера nb байтов и записывает адрес его начала в указатель p. Вызов FreeMem(p) освобождает динамическую память, контролируемую указателем p. Следует обратить внимание, что при вызове FreeMem не указывается размер освобождаемой памяти, поскольку в каждом выделенном блоке хранится его размер, и FreeMem пользуется этой информацией.
В большинстве ситуаций использования типизированных указателей и процедур New и Dispose оказывается достаточно. Процедуры GetMem и FreeMem применяются там, где требуется более гибкое управление памятью.
Пример. Динамический массив.
Динамическим будем называть массив, размер которого задается в процессе работы программы. В Delphi (начиная с версии 4) динамические массивы реализованы средствами языка:
var dyn: array of integer;
n: integer;
Begin
read(n);
Assert(n>0);
SetLength(dyn,n);
dyn[0]:=5;
...
Однако, динамические массивы нетрудно создать и с помощью обычных массивов с помощью процедур GetMem и FreeMem:
const sz=MaxInt div sizeof(integer);
type Arr: array [0..sz-1] of integer;
var dyn: ^Arr;
n: integer;
Begin
read(n);
Assert(n>0);
GetMem(dyn,n*sizeof(integer));
dyn^[0]:=5; // можно dyn[0]:=5
...
Идея подобной реализации динамического массива состоит в следующем. Описывается тип массива с большим количеством элементов и переменная dyn, являющаяся указателем на этот тип. С помощью GetMem выделяется нужное количество памяти, определяемое в процессе работы программы; адрес выделенной памяти записывается в переменную dyn. С этого момента можно обращаться к элементам массива, используя запись вида dyn^[0]. Операцию разыменования в Delphi можно опускать, поэтому с dyn можно обращаться как с обычным массивом: dyn[0]. В конце работы с таким массивом следует вызвать FreeMem(dyn).
Отметим, что при включенном режиме проверки выхода за границы диапазона {$R+} нельзя выделять под массив память, превосходящую его размер, то есть должно выполняться условие n<=sz. Поэтому следует задавать размер массива sz максимально возможным. В Delphi память, занимаемая переменной любого типа, не должна превосходить 2 Гб, т.е. MaxInt байт. Поскольку элементы массива имеют тип integer, то в качестве sz выбрано максимально возможное значение MaxInt div sizeof(integer).
Begin
pi^:=5;
Если pi – глобальная переменная, то она автоматически инициализируется нулевым значением, т.е. имеет значение nil. Разыменование нулевого указателя приводит к ошибке времени выполнения. Если pi – локальная переменная, то она по умолчанию не инициализируется, а поэтому содержит непредсказуемое значение. Это значение трактуется как адрес целой переменной, к которой осуществляется доступ. Как правило, в этой ситуации возникает исключение Access Violation (нарушение защиты доступа), но по чистой случайности может оказаться, что указатель pi содержит истинный адрес переменной программы, тогда переменная будет изменена, выполнение программы продолжится дальше, а факт изменения переменной непредсказуемым образом повлияет на дальнейшее выполнение программы.
2. «Висячие» указатели.
После освобождения динамической памяти указатель продолжает указывать на старое место. Такие указатели называются «висячими». Попытка записи по такому указателю не приводит к немедленной ошибке. Однако память, на которую он указывает, могла быть уже выделена другой динамической переменной, и попытка записи приведет к порче этой переменной.
var pi: ^integer;
Begin
New(pi);
pi^:=5;
Dispose(pi); // указатель становится "висячим"
...
pi^:=6; // ошибка!
Если после Dispose(pi) сразу написать pi:=nil, то в дальнейшем при попытке разыменовать нулевой указатель pi возникнет исключение, что является более предпочтительным, чем скрытая ошибка изменения другой переменной. Данный прием следует взять на вооружение и после освобождения динамической переменной обнулять указатель:
Dispose(pi);
pi:=nil;
3. «Утечка» памяти.
Данная ошибка возникает, когда память не освобождается, но перестает контролироваться указателем. Подобную ошибку называют «утечкой» памяти, поскольку такую память невозможно освободить. Такая ошибка труднонаходима, поскольку практически не сказывается на работе приложения. Однако при систематических утечках программа требует все больше памяти у операционной системы, замедляя работу других приложений. Далее приводятся две распространенные ситуации, в которых возникает утечка памяти.
Пример 1. Повторное выделение памяти.
Если выделить память повторно для того же указателя, то ранее выделенная память «утечет»:
var pi: ^integer;
Begin
New(pi);
pi^:=5;
New(pi);
Пример 2. Выделение памяти под локальную переменную без освобождения.
procedure pp;
var pi: ^integer;
Begin
New(pi);
end;
Данная процедура составлена ошибочно: локальный указатель pi уничтожается после завершения работы процедуры, поэтому контролируемая им динамическая память «утекает». Особенно опасна подобная утечка при вызове такой процедуры в цикле:
for i:=1 to MaxInt do
pp;
4. Память, выделенная динамически для глобальных переменных-указателей, не возвращается явно в конце программы.
Поскольку динамическая память автоматически освобождается в конце работы программы, отсутствие явного вызова Dispose или FreeMem для глобальных переменных-указателей на динамическую память не может считаться ошибкой и свидетельствует просто о неаккуратности программирования. Однако при переносе текста основной программы в процедуру мы получим ошибку утечки памяти, описанную в предыдущем пункте.
5. Попытка освободить динамическую память, не выделенную ранее.
var pi: ^integer;
Begin
Dispose(pi);
Подобная ошибка приводит к немедленной генерации исключения, поэтому не принадлежит к числу опасных. Заметим, что в Delphi вызов процедуры Dispose для нулевого указателя просто игнорируется, не приводя к генерации исключения.
6. Попытка дважды освободить занимаемую память.
var pi: ^integer;
Begin
New(pi);
...
Dispose(pi);
Dispose(pi);
При повторном вызове процедуры Dispose будет сгенерировано исключение.
7. Попытка освободить нединамическую память.
var pi: ^integer;
i: integer;
Begin
pi:=@i;
Dispose(pi);
При вызове Dispose для нединамической переменной будет сгенерировано исключение.
8. Выход за память, выделенную процедурой GetMem.
Поскольку GetMem выделяет количество памяти, не зависящее от размера объекта, с которым связан указатель, она менее безопасна, чем New. Например, при реализации с помощью GetMem динамического массива можно предпринять попытку обратиться за границы выделенной памяти:
GetMem(dyn,n*sizeof(integer));
dyn^[n+1]:=5;
Обычно такая ошибка приводит к исключению Access Violation.
Задание 1
Составить программу, которая решает одну из следующих задач, используя только переменные динамической памяти:
1. посчитать сумму цифр данного целого числа;
2. посчитать сумму делителей данного целого числа;
3. определить, является ли данное целое число простым;
4. посчитать N-е число Фибоначчи;
5. посчитать сумму первых N чисел Фибоначчи;
6. посчитать количество трехзначных чисел с суммой цифр 13.
Задание 2
Составьте программу, которая формирует максимально длинный одномерный массив целых чисел в динамической памяти и заполняет его случайными целыми числами из диапазона от 0 до 20.
Задание 3
Дополните предыдущую программу процедурой, которая проверяет на равномерность качество датчика случайных чисел Паскаля (для этого надо посчитать в сформированном массиве количество полученных 0, 1, 2 и т.д. и сравнить их между собой).
Задание 4
Составьте процедуру для упорядочения сформированного массива.
Лабораторная работа №11
Работа со списк ами
Теоретические сведения
Односвязные линейные списки
Для удобства определим вспомогательную функцию NewNode, создающую в динамической памяти узел линейного односвязного списка, заполняющую его поля значениями data и next и возвращающую указатель на него:
function NewNode(data: integer; next: PNode): PNode;
begin
New(Result);
Result^.data:=data;
Result^.next:=next;
end;
Основными действиями с линейным односвязным списком являются вставка, удаление, поиск элементов, проход по списку и сортировка. Будем считать, что во всех приводимых операциях указатель p типа PNode хранит адрес текущего элемента списка.
Если поле данных data элемента списка содержит значение x, то для простоты будем говорить, что элемент или узел имеет значение x.
1. Вставка элемента со значением x в начало списка.
Пусть первый элемент является текущим (указатель p хранит адрес первого элемента):
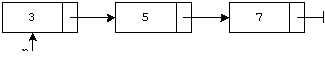
Создадим новый элемент со значением x, поле next которого указывает на первый элемент, после чего сделаем этот элемент первым, присвоив его адрес указателю p:
p:=NewNode(x,p);
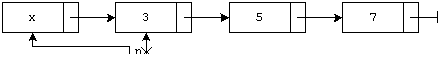
Отметим, что данная операция производит добавление также и в пустой список (p=nil). При многократном ее выполнении происходит заполнение списка, причем, элементы в списке будут располагаться в порядке, обратном порядку их включения.
2. Удаление элемента из начала непустого списка.
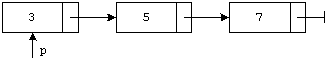
Запомним адрес первого элемента в переменной t, после чего переместим указатель на первый элемент вперед и освободим элемент, контролируемый указателем t:
t:=p;
p:=t^.next;
Dispose(t);
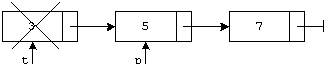
3. Вставка элемента со значением x после текущего.
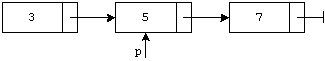
Данная операция аналогична вставке в начало, но вместо p используется p.next:
p^.next:=NewNode(x,p^.next);
4. Удаление элемента, следующего за текущим.
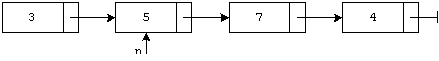
Данная операция аналогична удалению из начала, но вместо p используется p.next; если p.next=nil, то никаких действий не производится:
t:=p^.next;
if t<>nil then
begin
p^.next:=t^.next;
Dispose(t);
end;
5. Вставка элемента со значением x перед текущим.
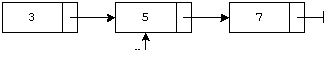
Вставим после текущего элемента его копию, затем присвоим полю данных текущего элемента значение x и передвинем текущий элемент вперед:
p^.next:=NewNode(p^.data,p^.next);
p^.data:=x;
p:=p^.next;
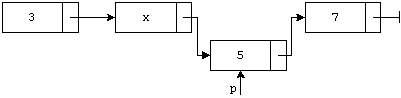
6. Удаление текущего элемента.
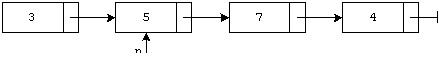
Для быстрого выполнения этого действия требуется, чтобы существовал элемент, следующий за текущим. Скопируем поле данных и поле next из следующего элемента в текущий, после чего освободим следующий:
t:=p^.next;
p^.data:=t^.data;
p^.next:=t^.next;
Dispose(t);
7. Проход по списку.
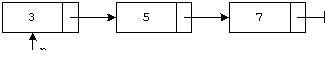
Пусть над всеми элементами списка необходимо выполнить некоторую операцию Oper, заданную процедурой с одним ссылочным параметром, например:
procedure Oper(var i: integer);
begin
i:=i*2;
end;
Установим указатель на его первый элемент и, пока значение указателя не равно nil, будем выполнять операцию Oper и передвигаться на следующий элемент:
while p<>nil do
begin
Oper(p^.data);
p:=p^.next;
end;
Очевидно, во время прохода по списку можно не только менять элементы, но и выводить их или производить вычисления: например, подсчитывать сумму или количество элементов, удовлетворяющих некоторому условию.
8. Поиск элемента со значением x.
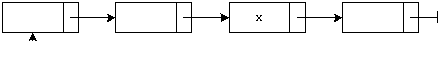
Проход по списку здесь надо совершать либо до конца списка, либо до момента, когда текущий элемент будет иметь значение x. Если после цикла текущий элемент не нулевой, то он содержит первое найденное значение x.
while (p<>nil) and (p^.data<>x) do
p:=p^.next;
found:=p<>nil;
Следует обратить внимание на то, что порядок следования операндов в операции and важен и для корректной работы последнего алгоритма в Delphi должен быть установлен ключ компиляции сокращенного вычисления логических выражений {$B-}.
9. Разрушение списка.
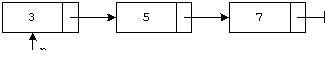
При разрушении мы удаляем элементы из начала списка до тех пор, пока список не станет пустым:
while p<>nil do
Begin
t:=p;
p:=p^.next;
Dispose(t);
end;
10. Вставка элемента в упорядоченный список с сохранением упорядоченности.
Пусть список не пуст и его элементы упорядочены по возрастанию. Чтобы вставить элемент со значением x с сохранением упорядоченности, найдем первый элемент с большим значением и произведем вставку перед ним. Для вставки перед элементом будем «заглядывать» на один элемент вперед, используя вместо переменной p выражение p^.next. Оформим данную операцию в виде процедуры:
procedure SortedListAdd(p: PNode; x: integer);
Begin
while (p<>nil) and (p^.next^.data<=x) do
p:=p^.next;
p^.next:=NewNode(x,p^.next);
end ;
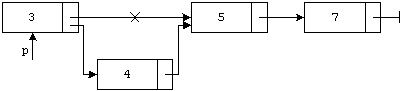
Отметим, что наш алгоритм осуществляет добавление после элемента, на который указывает p, поэтому он не может добавить в начало списка. Для решения указанной проблемы поместим в начало списка барьерный элемент, поле данных которого содержит самое маленькое число (-MaxInt). Список при этом сохранит свою упорядоченность, и теперь любой элемент будет добавляться после барьерного. Например, вот как выглядит заполнение упорядоченного списка n случайными числами с последующим его выводом:
readln(n);
p:=NewNode(-MaxInt,nil); // барьер
for i:=1 to n do
SortedListAdd(p,Random(1000));
t:=p;
while t<>nil do
Begin
write(t^.data);
t:=t^.next;
end;
По существу, приведенный код реализует алгоритм сортировки вставками. Поскольку при вставке одного элемента в список длины n может потребоваться n операций (в случае прохода по всему списку), то для вставки n элементов требуемое количество операций пропорционально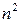 
.
Двусвязные линейные списки
Двусвязный линейный список состоит из элементов, каждый из которых хранит адреса следующего и предыдущего. Для удобства работы со списком поддерживаются указатели first и last на первый и последний элемент соответственно:
В структуру Node добавляется указатель prev на предыдующий элемент списка:
type
PNode=^Node;
Node=record
data: integer;
prev,next: PNode;
end;
Вспомогательная функция NewNode при этом изменяется очевидным образом:
function NewNode(data: integer; prev, next: PNode): PNode;
begin
New(Result);
Result^.data:=data;
Result^.next:=next;
Result^.prev:=prev;
end;
Рассмотрим основные операции с двусвязным списком, реализация которых отличается от односвязного. После выполнения каждой операции first и last должны по-прежнему оставаться указателями на начало и конец списка, а если список пуст, то получать нулевое значение.
1. Инициализация.
При инициализации список пуст:
first:=nil;
last:=nil;
2. Добавление элемента со значением x в начало.
Осуществляется аналогично добавлению в односвязный список. Если список был пустым, то last также должен указывать на добавленный элемент.
first:=NewNode(x,nil,first);
if last=nil then last:=first;
3. Добавление элемента со значением x в конец.
Симметрично добавлению в начало:
last:=NewNode(x,last,nil);
if first=nil then first:=last;
4. Вставка элемента со значением x перед текущим.
Пусть указатель p хранит адрес текущего элемента.
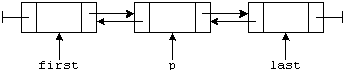
Создадим новый элемент, поле next которого указывает на текущий, поле prev – на предыдущий. При этом поле prev текущего элемента и поле next предыдущего должны указывать на вставляемый. Если же предыдущего элемента нет, то осуществляется вставка в начало, и требуется скорректировать указатель на первый элемент:
t:=NewNode(x,p^.prev,p);
p^.prev:=t;
if p^.prev<>nil then
p^.prev^.next:=t
else first:=t;
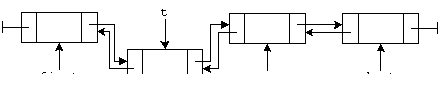
Аналогично производится вставка после текущего элемента.
5. Удаление текущего элемента.
Пусть указатель p хранит адрес текущего элемента.
Перед освобождением памяти под текущий элемент следует перенаправить указатель next у предыдущего элемента на следующий, а у следующего указатель prev –на предыдущий. Если же следующего элемента нет, то необходимо удалить последний элемент и скорректировать переменную last. Аналогично если предыдущего элемента нет, то удаляется первый, и необходимо скорректировать first.
if p^.prev<>nil then
p^.prev^.next:=p^.next
else first:=p^.next;
if p^.next<>nil then
p^.next^.prev:=p^.prev
else last:=p^.prev;
Dispose(p);
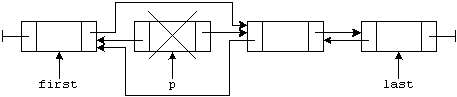
Заметим, что если удаляется единственный элемент, то указатели first и last получают значение nil, т.е. список становится пустым.
В заключение приведем пример, иллюстрирующий высокую эффективность списков в некоторых задачах.
Пример. Объединение списков.
Имеется два списка, заданные указателями на начало и конец.
Требуется добавить содержимое второго списка в конец первого, очистив при этом второй список.
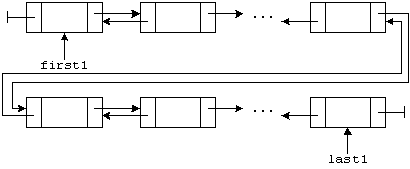
Для решения указанной задачи достаточно выполнить всего пять операторов присваивания:
last1^.next:=first2;
first2^.prev:=last1;
last1:=last2;
first2:=nil;
last2:=nil;
Заметим, что решение аналогичной задачи для массива требует использования цикла с числом итераций, равным размеру добавляемого массива.
Задание 1
Составить процедуры ввода и печати двунаправленного списка, опробовать их работу.
Задание 2
Составить нерекурсивную функцию для:
2.1. Подсчета числа элементов в списке
2.2. Нахождения суммы элементов списка
2.3. Нахождения максимума в непустом списке
2.4. Нахождения минимума в непустом списке
2.5. Поиска данного числа среди элементов списка (логическая функция)
2.6. Нахождения произведения ненулевых элементов списка
Задание 3
Составить аналогичную предыдущей рекурсивную функцию.
Задание 4
Выполнить одно из следующих заданий:
4.1. Составить процедуру добавления элемента в упорядоченный список с сохранением свойства упорядоченности списка. Проверить работу процедуры, а затем с ее использованием составить программу упорядочивания списка.
4.2. Составить процедуру смены местами двух последовательных элементов списка (аргументы – указатели на начало, конец списка и на первый из меняемых элементов, результат – указатели на начало и конец нового списка). Опробовать работу процедуры, а затем с ее помощью упорядочить данный список методом «пузырька».
Задание 5
Решить одну из следующих задач:
5.1. Составить процедуру слияния двух упорядоченных списков в один и с ее помощью организовать быструю сортировку списка.
5.2. Реализовать процедуру выбора водящего с помощью детской считалочки по кругу с выбыванием (после выбывшего счет начинается заново со следующего по кругу, а последний оставшийся и есть водящий).
5.3. Восстановить список, если есть список всех пар следующих друг за другом элементов, например по данным (4,13),(5,7),(7,3),(13,5),(67,4) должен быть получен исходный список (67,4,13,5,7,3).
Задание 6
Имеется указатель на первый элемент однонаправленного списка. Последний элемент списка указывает на nil. Описать алгоритм, (аккуратно, но не доводя до программы), с помощью которого можно установить корректность списка или наличие в нем циклов.
Лабораторная работа №12
Работа с графикой
Цель: приобрести навыки работы с графическими возможностями среды программирования.
Теоретические сведения
Дополнительные ресурсы:
http://www.slideshare.net/yak-ella/pascal-abc
http://samlib.ru/w/waleri_l_w/grafikawpascalabc.shtml
Изображения в паскале можно создавать с помощью модуля GraphABC, он подключается после Uses.
Начнем с рассмотрения системы координат в паскале
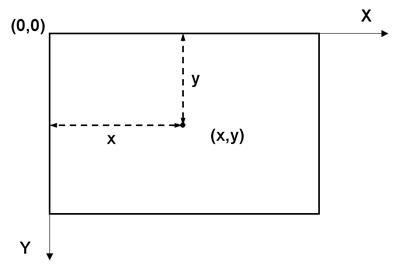
Операторы используемые в графике:
SetWindowHeight(h); - Устанавливает высоту графического окна
SetWindowWidth(w); - Устанавливает ширину графического окна
ClearWindow; - очищает графическое окно белым цветом.
ClearWindow(color); - очищает графическое окно указанным цветом.
SetPixel(x,y,color); - Закрашивает один пиксел с координатами (x,y) цветом color
LineTo(x,y); - рисует отрезок от текущего положения пера до точки (x,y); координаты пера при этом также становятся равными (x,y).
Line(x1,y1,x2,y2); - рисует отрезок с началом в точке (x1,y1) и концом в точке (x2,y2).
SetPenColor(color); - устанавливает цвет пера, задаваемый параметром color.
Некоторые из цветов:
| clBlack – черный clPurple – фиолетовый clWhite – белый clMaroon – темно-красный clRed – красный clNavy – темно-синий clGreen – зеленый clBrown – коричневый clBlue – синий clSkyBlue – голубой clYellow – желтый clCream – кремовый | clAqua – бирюзовый clOlive – оливковый clFuchsia – сиреневый clTeal – сине-зеленый clGray – темно-серый clLime – ярко-зеленый clMoneyGreen – цвет зеленых денег clLtGray – светло-серый clDkGray – темно-серый clMedGray – серый clSilver – серебряный |
Цвет также можно задать с помощью палитры RGB для это за место color пишется rgb(r,g,b): где r,b,g - числа от 0 до 255
SetPenWidth(n); - устанавливает ширину (толщину) пера, равную n пикселям.
Rectangle(x1,y1,x2,y2); - рисует прямоугольник, заданный координатами противоположных вершин (x1,y1) и (x2,y2).
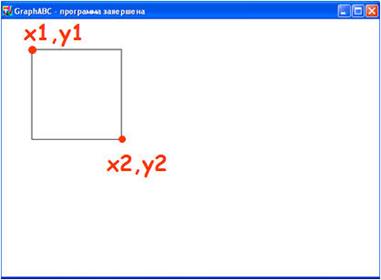
FloodFill(x,y,color); - заливает область одного цвета цветом color, начиная с точки (x,y).
SetBrushColor(color); - устанавливает цвет кисти, заливка кистью распространяется на замкнутый контур, описание которого следует за процедурой установки цвета кисти.
Circle(x,y,r); - рисует окружность с центром в точке (x,y) и радиусом r.
Ellipse(x1,y1,x2,y2); - рисует эллипс, заданный своим описанным прямоугольником с координатами противоположных вершин (x1,y1) и (x2,y2).
SetFontName(‘name’);- устанавливает наименование шрифта.
SetFontColor(color); - устанавливает цвет шрифта.
SetFontSize(sz); - устанавливает размер шрифта в пунктах.
SetFontStyle(fs); - устанавливает стиль шрифта.
Стиль шрифта:
fsNormal – обычный;
fsBold – жирный;
fsItalic – наклонный;
fsBoldItalic – жирный наклонный;
fsUnderline – подчеркнутый;
fsBoldUnderline – жирный подчеркнутый;
fsItalicUnderline – наклонный подчеркнутый;
fsBoldItalicUnderline – жирный наклонный подчеркнутый.
Пример: нарисовать
Программа:
Program Seventh;
uses GraphABC;
Begin
Line (200,200,400,200); LineTO (300,140); lineTO (200,200);
FloodFill (300,170,clblue);
Line (200,200,400,200); LineTo (300,260); LineTo (200,200);
FloodFill (300,230,cllime);
circle (160,200,40);
FloodFill (160,200,clred);
circle (440,200,40);
FloodFill (440,200,clyellow);
End.
На экране вы увидите:
Задание 1.
Построить график функции. Реализовать координатную сетку, оси координат, и линию графика функции y = f(x).
а) График рисуется по точкам (приращение координаты ∆x = 1).
б) График функции рисуется в виде ломаной линии. Прорисовать в виде отдельных отрезков, приращение координаты (∆x = 5).
| № варианта | f(x) |
| 1 | sin(x) + 2*x |
| 2 | cos(x) |
| 3 | tg(x) |
| 4 | 2x2 + 3x - 5 |
| 5 | 4x3 – 5x - 2 |
| 6 | 2 * log2x |
| 7 | ex – 5*x |
| 8 | 5*x – 6*x2 |
| 9 | 4*x3 – sin(x) |
| 10 | 2* sin(x) + 3*cos(s) |
Задание 2.
Прорисовать изображение:
| № варианта | f(x) |
| 1 | автомобиль |
| 2 | самолёт |
| 3 | арбуз |
| 4 | дом |
| 5 | дерево |
| 6 | шляпа |
| 7 | телефон |
| 8 | книга |
| 9 | очки |
| 10 | карандаш |
На форме должно быть изображение и крупная цветная надпись с названием изображения.
Задание 3.
Реализовать программу, которая прорисовывает на форме сетку ( 10 х 10 ячеек).
Программа открывает файл в котором содержится значение цвета для каждой ячейки. В соответствие с файлом ячейки сетки на форме заполняются нужными цветами. В файле для отображения цветов используются символы:
R – красный;
G – зелёный;
B – голубой.
Например:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | ||||||||||
| 2 | ||||||||||
| 3 | ||||||||||
| 4 | ||||||||||
| 5 | ||||||||||
| 6 | ||||||||||
| 7 | ||||||||||
| 8 | ||||||||||
| 9 | ||||||||||
| 10 |
Файл содержит:
RRRRRRRRRR
RRRRRRRRRG
RRRRRRRRGG
RRRRRRRGGG
RRRRRRGGGG
RRRRRGGGBB
RRRRGGGBBB
RRRGGGBBBB
RRGGGBBBBB
RGGGBBBBBB
Лабораторная работа №13
Работа с графикой, анимация
Цель: закрепить навыки работы с графическими функциями, приобрести опыт реализации динамических графических изображений.
Теоретические сведения
Рисование шара
| uses GraphABC; var I,X,Y,D: integer; begin X:=20; Y:=30; D:=100; ClearWindow; SetBrushColor(clGreen); Ellipse(X+I,Y,X+I+D,Y+D); end. |
Движение шара
uses GraphABC;
var I,X,Y,D : integer;
begin
X:=20; Y:=30; D:=100;
for i:=1 to 500 do
begin
ClearWindow;
SetBrushColor(clGreen);
Ellipse(X+I,Y,X+I+D,Y+D);
Sleep(1);
end;
end.
При работе данного примера возможно мерцание движущегося изображения. Для устранения этого эффекта используются следующие функции:
LockDrawing – блокирует вывод в графическое окно, осуществляя рисование только во внеэкранном буфере.
Redraw – перерисовывает окна вывода при заблокированном выводе в графическое окно.
Столкновение двух шаров
( один шар движется, другой покоится )
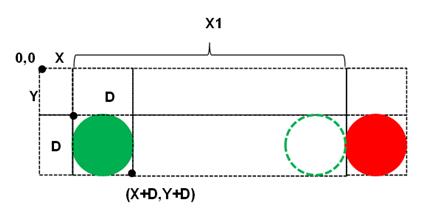
uses GraphABC;
var I,X,Y,D,X1,X2: integer;
begin
X:=20;
Y:=30;
D:=70;
X1:=350;
X2:=500;
LockDrawing;
for I:=1 to X1-D do
// зеленый шар движется, красный стоит на месте
begin
ClearWindow;
SetBrushColor(clGreen);
Ellipse(X+I,Y,X+I+D,Y+D);
SetBrushColor(clRed);
Ellipse(X+X1,Y,X+X1+D,Y+D);
Redraw;
Sleep(5);
end;
for I:=X1 to X2 do
// зеленый шар стоит на месте, красный шар движется
begin
ClearWindow;
SetBrushColor(clGreen);
Ellipse(X+X1-D,Y,X+X1,Y+D);
SetBrushColor(clRed);
Ellipse(X+I,Y,X+I+D,Y+D);
Redraw;
Sleep(5);
end;
end.
Задания .
В соответствие со своим вариантом реализовать анимированное изображение.
| № | Описание |
| 1. | Реализовать часы с маятником (использовать модель математического маятника, движение секундной, минутной и часовой стрелок.). Время на часах должно совпадать с системным временем на ПК. |
| 2. | Реализовать вывод текста из текстового файла на экран с эффектом с эффектом прокрутки и уменьшения каждой новой строки (как в StarWars) |
| 3. | Реализовать анимацию падающего мячика (мяч двухцветный). Мяч брошен под углом 45° к горизонту. |
| 4. | Реализовать смайлик, который реагирует на вводимые с клавиатуры слова (не менее 5 разных реакций: радость, грусть, удивление, обида, злость и др.). В текстовом файле заранее задан список слов, на которые реагирует смайлик. |
| 5. | Реализовать анимацию: падение предмета в воду. (изображение изометрическое, поэтому круги представляют собой овалы). |
| 6. | Реализовать модель солнечной системы. При помощи кнопок «+» и «-» можно ускорять и замедлять движение планет. Орбиты планет Эллиптические. |
| 7. | Реализовать «детский рисунок» : туча, дождь, цветок. (туча перемещается слева-направо, затем справа-налево; дождь идёт из тучи, капли падают на землю; цветок качается) |
| 8. | Реализовать бесконечные соударения двух шаров в замкнутом контуре. ( шары соударяются между собой и со стенками контура. Шары могут соударяться под любыми углами (является грубой моделью бильярда, в котором не действуют силы трения). |
| 9. | Реализовать «рулетку». (круглый барабан, на котором расположены цифры от 1 до 10. При старте программы барабан запускается и движется с замедлением пока полностью не остановится. После остановки на экране должна отобразиться цифра, напротив которой остановился барабан. Каждый раз значение должно быть разным (для этого использовать random). |
| 10. | Реализовать игру. Движение объекта (закрашенный прямоугольник) по экрану происходит при помощи стрелок клавиатуры. На экране в случайном порядке появляются объекты (закрашенные круги). При соприкосновении круга и прямоугольника круг исчезает и на экране отображается количество исчезнувших кругов (очки игры). Игра продолжается бесконечно. |
СОДЕРЖАНИЕ
| ЛАБОРАТОРНАЯ РАБОТА № 1 Логические операции. Основные законы | 3 |
| ЛАБОРАТОРНАЯ РАБОТА № 2 Булевы функции. Многочлены Жегалкина. | 15 |
| ЛАБОРАТОРНАЯ РАБОТА № 3 Эффективное кодирование неравновероятных символов источника дискретных сообщений | 33 |
| ЛАБОРАТОРНАЯ РАБОТА № 4 Команды ветвления и повторения на языке Паскаль | 38 |
| ЛАБОРАТОРНАЯ РАБОТА № 5 Одномерные массивы | 46 |
| ЛАБОРАТОРНАЯ РАБОТА № 6 Работа со строковыми величинами | 55 |
| ЛАБОРАТОРНАЯ РАБОТА № 7 Программирование с использованием процедур и функций | 62 |
| ЛАБОРАТОРНАЯ РАБОТА № 8 Работа с текстовыми файлами и файлами прямого доступа | 71 |
| ЛАБОРАТОРНАЯ РАБОТА № 9 Рекурсивные функции | 72 |
| ЛАБОРАТОРНАЯ РАБОТА № 10 Работа с динамической памятью. | 76 |
| ЛАБОРАТОРНАЯ РАБОТА № 11 Работа со списками | 92 |
| ЛАБОРАТОРНАЯ РАБОТА № 12 Работа с графикой | 104 |
| ЛАБОРАТОРНАЯ РАБОТА № 13 Работа с графикой, анимация | 109 |
Игнатенко Владимир Александрович
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ
Имени В.Я.ГОРИНА»
Кафедра информатики и информационных технологий
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ
к выполнению лабораторно-практических и самостоятельных работ
по дисциплине
«ИНФОРМАТИКА И ПРОГРАММИРОВАНИЕ»
для студентов экономического факультета
Дата: 2019-02-02, просмотров: 727.
