Рассмотрим падение на входной торец волновода пучка Лагерра-Гаусса, который содержит оптический вихрь с топологическим зарядом 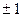, локализованного в точке с координатами :

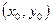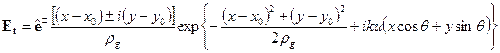. (1)

Используя уравнение (1) для падения на входной торец оптического вихря и поля собственных мод, получим коэффициенты возбуждения собственных мод:

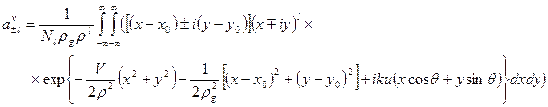, (2)

где « 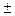» в квадратных скобках обозначает топологический заряд падающего пучка, а « 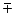» в круглых скобках соответствует топологическому заряду направляемого вихря, взятому со знаком «-». Формула (2) для падающего пучка с топологическим зарядом +1 перепишется в виде:

,

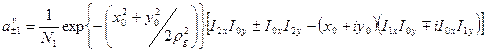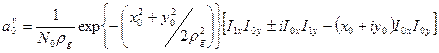.              (3)

где

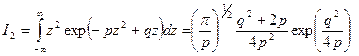,                (4)

Для падающего пучка с топологическим зарядом –1 все знаки в формулах (3), кроме знака «-» при скобке 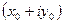, изменятся, включая знак в этой скобке. Исходный пучок, несущий вихрь с положительным топологическим зарядом, даст следующие выражения

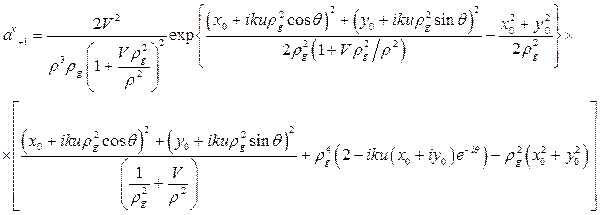
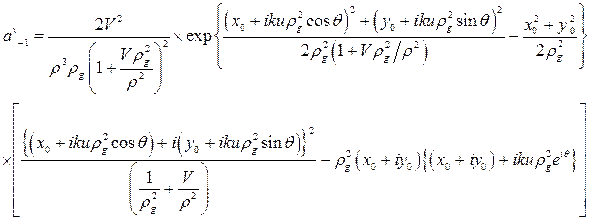, (5)

.

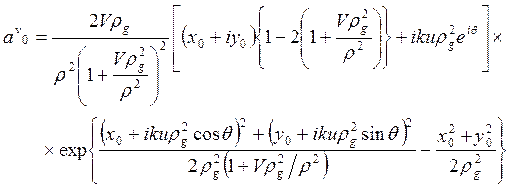Формулы (5) учитывают одновременно и смещение пучка и наклон его оси. Поскольку (5) имеют сложный вид, рассмотрим два частных случая. В первом из них будем полагать, что оси пучка и волокна параллельны (u=0). В этом случае коэффициенты возбуждения направляемых вихрей при падении пучка с оптическим вихрем можно переписать в виде

,

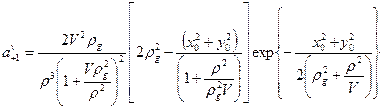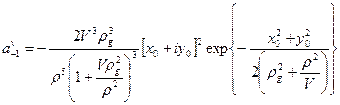,                    (6)

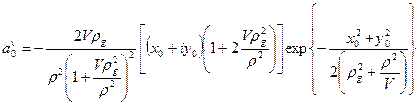
Во втором случае центры падающего пучка и волокна совпадают (x₀=0,y₀=0), а оси образуют угол u. Тогда коэффициенты возбуждения примут следующий вид

,

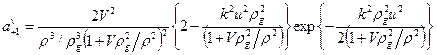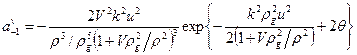,       (7)

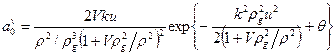
Написание программы.

Задание: построить графики зависимостей модуля коэффициента возбуждения мод(l=‑1,0,1) пучком с оптическим вихрем (l=+1) от смещения x_o в мкм (0..3.5), угла наклона пучка u в градусах (0..10). Параметры волокна: V=3.6 для l=0.63 мкм, r=3.5 мкм, радиус перетяжки пучка r _g=2 мкм (y_o =0, ).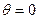

Рис. 5. Вид окна программы, с результатами выполнения задания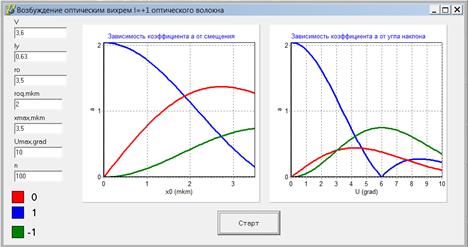

ПРАКТИЧЕСКОЕ ЗАДАНИЕ 5.

Построение распределение интенсивности в маломодовом оптическом волокне при возбуждении его гауссовым пучком

Теоретическое описание.

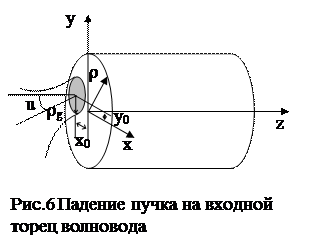Рассмотрим падение циркулярно поляризованного гауссова пучка на входной торец круглого маломодового волоновода под углом U, смещенного на расстояние x0 из центра. Для простоты рассмотрим градиентный профиль показателя преломления и волокно с V=3.6, в котором возбуждаются собственные моды с l=0,1. Необходимо построить распределение интенсивности и поляризации на выходном торце волокна длиной z.  

,

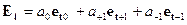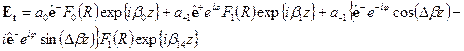
где , , , ,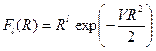

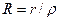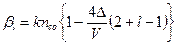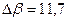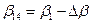
Написание программы.

Написание программы. На форму поместить 3 Image для построения интенсивности, эллиптичности 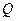 и азимутального угла  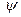в распределении поляризации. Задать начальные условия и параметры волокна ( 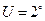, , 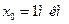V=3.6 для l=0.63 мкм, r=3.5 мкм 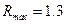, 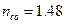) . Поместить кнопку для построения распределения интенсивности , 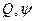, а также кнопку для построения эллипсов на 1-м image. После считывания параметров рассчитать коэффициенты возбуждения собственных мод волокна (см. задание 3), а затем в цикле рассчитать действительные и мнимые части полей E_x, E_y :

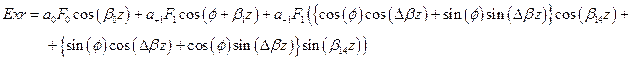
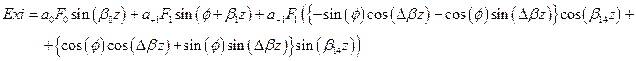
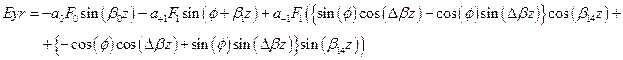
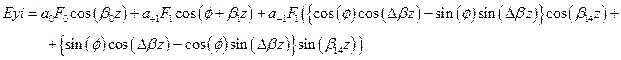
После чего необходимо рассчитать интенсивность, эллиптичность и угол 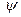 в каждой точке поля. .

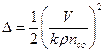Рис. 7. Вид окна программы, с результатами выполнения задания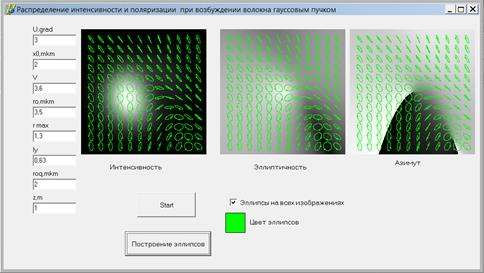

ПРАКТИЧЕСКОЕ ЗАДАНИЕ 6.