В ступенчатом круглом оптическом волокне со ступенчатым профилем показатель преломления распределяется следующим образом:
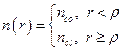, (1)
а радиальная зависимость собственных мод имеет вид:
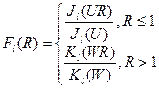, (2)
где Jl,Kl – функция Бесселя первого рода и модифицированная функция Бесселя второго рода, или функция Макдональда, U,W – волноводные параметры моды в сердцевине и оболочке, связанные соотношением
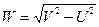, (3)
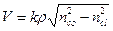- волноводный параметр волокна, l – азимутальный индекс моды.
Характеристическое уравнение получается из равенства тангенциальных составляющих электрического E и магнитного H полей на границе раздела 2-х сред (сердцевина – оболочка) и в данном случае для слабонаправляющих волокон в нулевом приближении (без учета поляризационных поправок) имеет вид
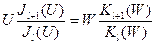. (4)
Для решения характеристического уравнения применяется графический метод. Берется по оси абсцисс параметр V в интервале от 0 до 5, по оси ординат – U в том же интервале. Для данного диапазона азимутальное число l изменяется в пределах от 0 до 2. Данный интервал разбивается на количество точек в графике (например, 300). Затем в двойном цикле по этим точкам графика (внешний – по V, внутренний – по U (проверяем, чтобы U<=V)) вычисляется значение функции f, равной разности правой и левой части уравнения (3) и сравнивается с предыдущим значением во 2-м цикле. Если их произведение <0, то на данном интервале (2-х точек) выполняется равенство (3) и в данном пикселе графика мы ставим закрашенную точку). Однако следует учесть, что в данном диапазоне при равенстве функции Бесселя J нулю в функции f будут происходить разрывы второго рода, для которых произведение f.f0<0, поэтому мы ограничиваем значение функции малым пределом (например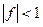 
).
Написание программы.
Для построения решения характеристического уравнения на форму помещаем квадратный Image (например, 400Х400 пикселов) по осям проставляет диапазон значений по V,U (0..5) и сами переменные (в Label). Цвет Image определяем как белый. Помещаем кнопку для процесса вычисления.
Внутренний цикл вычисления будет выглядеть так:
| Блок 1.1. Расчет характеристической кривой | n:=300; Form1.Image1.Width:=n; Form1.Image1.Height:=n; Form1.Image1.Canvas.Brush.Color:=clwhite; Form1.Image1.Canvas.FillRect(Rect(0,0,image1.Width,image1.Height)); {очистка Image} Vmax:=5; for l:=0 to 2 do Begin for i:=1 to n do begin f:=0; V:=Vmax/n*i; for j:=0 to i do begin U:=Vmax/n*j; W:=sqrt(sqr(V)-sqr(U)); f0:=f; If Bessel_J(l,U)=0 then f:=0 else f:=U*Bessel_J(l+1,U)/Bessel_J(l,U)- W*Bessel_K(l+1,W)/Bessel_K(l,W); if f0*f<0 then Form1.Image1.Canvas.Pixels[I,n-j]:=col[l]; end; end; end; |
Дополнительно проводится линия V=W:
| Блок 1.2. Проведение линии W=V | Form1.Image1.Canvas.Pen.Color:=clblack; Form1.Image1.Canvas.MoveTo(0,0); Form1.Image1.Canvas.LineTo(n,n); |
Цвета линий имеют тип Col: array[0..2] of Tcolor; и определяются в процедуре Form1.Create как
| Блок 1.3. Цвета линий хар. кривой | Col[0]:=clred; Col[1]:=clblue; Col[2]:=clgreen; |
Конечно можно выбрать другие три цвета и на форме указать какой цвет соответствует какому азимутальному числу l моды.
Процедуры для вычисления функций Бесселя имеют вид:
| Блок 1.5. Вычисление фунции Бесселя Jn(x) | function Bessel_J(n: integer;x: real):real; var xx,sx,Ln1,Ln,zn,sm,lm,dJn:real; ic,s: integer; label 1; begin xx:=x/2;sx:=1; for ic:=1 to n do sx:=sx*xx/ic; Ln:=1; s:=-1; sm:=1; zn:=1; ic:=1; 1: Ln1:=Ln; sm:=sm*xx*xx; zn:=zn*(n+ic)*ic; lm:=s*sm/zn; Ln:=Ln+lm; s:=-s; dJn:=abs(Ln-Ln1); ic:=ic+1; if dJn>0.0001 then goto 1; Ln:=Ln*sx; Bessel_J:=Ln; end; |
ПРИМЕЧАНИЕ: Представленный алгоритм (блок 1.5.) использует не рекомендуемую функцию GOTO 1, рекомендуется переписать эту функцию с использованием операторов цикла While – do или Repeat – until
| Блок 1.6. Вычисление фунции Бесселя Kn(x) | function Bessel_K(n: integer;x: real):real; var t,dt,kn,v,chv,fk,f1,cv,fk1,dKn,Kn1: real; label 2; begin t:=0;dt:=0.1;Kn:=0; 2: Kn1:=Kn; v:=t; chv:=(exp(v)+exp(-v))/2; v:=t*n; cv:=(exp(v)+exp(-v))/2; f1:=exp(-x*chv)*cv; fk:=f1*dt; t:=t+dt; v:=t; chv:=(exp(v)+exp(-v))/2; v:=t*n; cv:=(exp(v)+exp(-v))/2; f1:=exp(-x*chv)*cv; fk1:=f1*dt; Kn:=Kn+(fk+fk1)/2; dKn:=Kn-Kn1; if dKn>0.0001 then goto 2; Bessel_K:=Kn; end; |
ПРИМЕЧАНИЕ: Представленный алгоритм (Блок 1.6.) использует не рекомендуемую функцию GOTO 1, рекомендуется переписать эту функцию с использованием операторов цикла While – do или Repeat – until
| Рис. 1. Вид окна программы, с результатами выполнения задания |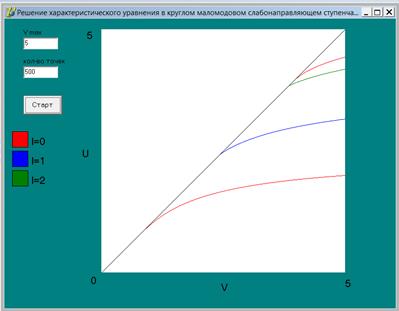 
|
ПРАКТИЧЕСКОЕ ЗАДАНИЕ 2.
Дата: 2019-02-02, просмотров: 228.
