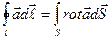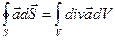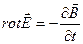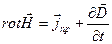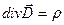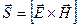Вопросы для самоконтроля .
1. В чем заключается максвелловская трактовка явления электромагнитной индукции?
2. Что называется током смещения?
3. Напишите систему уравнений Максвелла в интегральной и дифференциальной формах. В чем состоит физический смысл каждого уравнения?
4. Напишите волновые уравнения для электромагнитного поля и их решения.
5. Перечислите Основные свойства электромагнитных волн.
6. Что называется вектором Пойнтинга? Каков его физический смысл?
7. нарисуйте диаграмму направленности излучения диполя.
ОПТИКА
Лекция № 31
РАСПРОСТРАНЕНИЕ СВЕТА ЧЕРЕЗ ГРАНИЦУ ДВУХ СРЕД
План
1. Электромагнитная природа света. Принцип Гюйгенса. Абсолютный показатель преломления. Законы отражения и преломления. Относительный показатель преломления
2. Полное внутреннее отражение. Световоды.
3. Геометрическая оптика как предельный случай волновой оптики.
Свет с волновой точки зрения, как уже отмечалось в Лекции №30,
п.3, - электромагнитная волна. С одной стороны светого диапазона шкалы электромагнитных волн – рентгеновское излучение (за ультрафиолетовой областью). Что же касается видимого света, то это достаточно узкий интервал длин электромагнитных волн, заключенных примерно между 400 и 800 нм. Они действуют непосредственно на человеческий глаз и вследствие этого, указанный интервал играет особую роль для человека.
Принцип Гюйгенса устанавливает способ построения фронта волны в момент 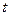 +
+ 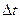 по известному положению в момент
по известному положению в момент 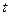 (рис. 31.1).
(рис. 31.1).
Каждая точка, до которой доходит волновое движение, служит центром
 |
Законы отражения и преломления.
Линии, вдоль которых распространяется световая энергия, называется лучами.В изотропных средах направление распространения световой энергии совпадает с направлением волнового вектора 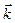 . (Напомним, что вектор
. (Напомним, что вектор 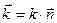 . равный по модулю волновому числу
. равный по модулю волновому числу 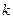 = 2πۤ/λ и имеющий направление по нормали к волновой поверхности)
= 2πۤ/λ и имеющий направление по нормали к волновой поверхности)



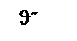

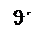
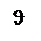
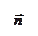
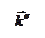
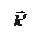
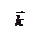
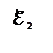
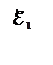





 При падении плоской световой волны (
При падении плоской световой волны ( 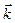 ) на на плоскую границу раздела двух однородных и изотропных диэлектриков (рис. 31.2) кроме
) на на плоскую границу раздела двух однородных и изотропных диэлектриков (рис. 31.2) кроме
 |
плоскостью падения волны. Энергия, которую несет с собой падающий луч, распределяется между отраженным и преломленным лучами. На рис. 31.2 ϑ, ϑ΄и ϑ˝ собственные углы падения, отражения и преломления световой волны.
Отношение скорости световой волны в вакууме к фазовой скорости υ в некоторой среде называется абсолютным показателем преломления этой среды и обозначается 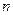 .
.
|

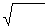
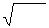
 Так как υ = 1/ ℰ∙μ∙ℰ
Так как υ = 1/ ℰ∙μ∙ℰ 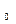 ∙μ
∙μ 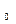 (см. лекцию №39), а для вакуума ℰ = 1, μ = 1 и с = 1/ ℰ
(см. лекцию №39), а для вакуума ℰ = 1, μ = 1 и с = 1/ ℰ 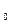 μ
μ 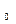 , то υ = с / ℰμ , отсюда
, то υ = с / ℰμ , отсюда 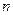 = ℰμ .
= ℰμ .
Для прозрачных веществ можно считать μ 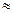 1, тогда
1, тогда
 |
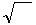
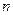
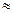 ℰ
ℰ
Законы отражения и преломления. Относительный показатель
Преломления.
Закон отражения света: отраженный луч лежит в одной плоскости с па
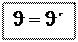 дающим лучом и нормалью, восстановленной в точке падения; угол отражения равен углу падения
дающим лучом и нормалью, восстановленной в точке падения; угол отражения равен углу падения
Закон преломления: преломленный луч лежит в одной плоскости с па
|
|
Замечание. законы отражения и преломления вытекают из так называемого принципа Ферма (французский ученый, 17 век, не путать с теоремой Ферма). Он представляет в геометрической оптике аксиому, именуемую принципом кратчайшего оптического пути (или минимального времени распространения) – утверждение, что луч света всегда распространяется в пространстве между двумя точками по тому пути, вдоль которого время его прохождения меньше, чем вдоль любого из других путей, соединяющих эти точки.
2. Полное внутреннее отражение. Световоды.
При переходе света из оптически более плотной среды в оптически менее плотную ( 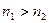 ) преломленный луч удаляется от нормали к поверхности раздела сред. Увеличение ϑ сопровождается более быстрым ростом угла преломления ϑ˝, и по достижении угла ϑ значения
) преломленный луч удаляется от нормали к поверхности раздела сред. Увеличение ϑ сопровождается более быстрым ростом угла преломления ϑ˝, и по достижении угла ϑ значения
|

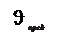

 (31-1)
(31-1)
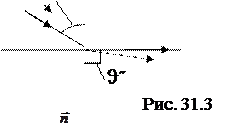 |
волна проникает во вторую среду на расстояние порядка длины волны λ и затем возвращаются в первую среду. Это явление называется полным внутреннем отражением.











































 Световоды. Явление полного внутреннего отражения используется в световодах, представляющих собой тонкие нити (волокна) из оптически прозрачного материала. Оптическое волокно состоит из сердцевины и оболочки. Свет, падающий на торец световода (рис. 31.4) под углами,
Световоды. Явление полного внутреннего отражения используется в световодах, представляющих собой тонкие нити (волокна) из оптически прозрачного материала. Оптическое волокно состоит из сердцевины и оболочки. Свет, падающий на торец световода (рис. 31.4) под углами,
 |
щей жиле (сердцевине). С помощью световодов можно произвольным образом исправлять путь светового пучка. Для передачи изображений применяется, как правило, многочисленные световоды. Вопросы передачи световых волн и изображений изучаются в специальном разделе оптики – волоконной оптике.
Световоды применяются кроме всего в волоконно-оптических линиях связи.
Примечание. В чем преимущество диапазона по сравнению с радиопаозоном?
При передаче информации модулированными электромагнитными колебаниями необходимо, чтобы частота модуляции была в 10..100 раз меньше несущей частоты. Кроме того, частоты модуляции занимают некоторую полосу частот. Так, для передачи музыкальной программы нужна полоса от 10 Гц до 10 кГц. Поэтому, несущая частота не может быть меньше 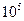 Гц. Для передачи одного телевизионного канала требуется полоса частотой около
Гц. Для передачи одного телевизионного канала требуется полоса частотой около 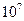 Гц. Так что, для передачи телевизионного изображения нужна несущая частота ≈
Гц. Так что, для передачи телевизионного изображения нужна несущая частота ≈ 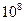 Гц. Частота видимого излучения около
Гц. Частота видимого излучения около 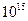 Гц, поэтому информационная емкость канала связи может быть многократно увеличена. По оптическому кабелю можно вести одновременно десятки тысяч телефонных разговоров, передавать сотни телевизионных программ (теоретически до
Гц, поэтому информационная емкость канала связи может быть многократно увеличена. По оптическому кабелю можно вести одновременно десятки тысяч телефонных разговоров, передавать сотни телевизионных программ (теоретически до 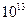 телефонных разговоров или
телефонных разговоров или 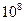 телевизионных программ [ ], реально, конечно, немного меньше, но все равно эти цифры впечатляют).
телевизионных программ [ ], реально, конечно, немного меньше, но все равно эти цифры впечатляют).
Вопросы для самоконтроля.
1. Что называется абсолютным, относительным показателями преломления?
2. Сформулируйте законы отражения и преломления.
3. В чем заключается явление полного внутреннего отражения?
4. Как устроен световод? Его применение.
5. При каких условиях можно использовать приближение геометрической оптики?
Лекция № 32
ИНТЕРФЕРЕНЦИЯ СВЕТА
План
1. Интерференция света. Когерентность и монохроматичность световых волн. Временная когерентность. Время и длина когерентности.
2. Пространственная когерентность. Радиус когерентности.
3. Оптическая длина пути. Оптическая разность хода. Расчет интерференционной картины от двух когерентных источников.
4. Полосы равной толщины и равного наклона.
Вопросы для самоконтроля.
1. В чем состоит явление интерференции?
2. Что такое когерентность?
3. В чем состоит временная когерентность?
Каков смысл времени и длины когерентности?
4. В чем состоит пространственная когерентность?
Каков смысл радиуса когерентности?
5. Что называется оптической длиной пути
и оптической разностью хода?
6. Каковы условия получения интерференционных максимумов и мини-
мумов при положении света от двух когерентных источников?
7. Как получаются полосы равной толщины и равного наклона?
Лекция № 33
ДИФРАКЦИЯ СВЕТА
План
1. Дифракция света. Принцип Гюйгенса-Френеля. Дифракция Френеля и Фраунгофера. Метод зон Френеля. Прямолинейное распространение света. Дифракция Френеля на круглом отверстии и диске.
2. Дифракция Фраунгофера на одной щели.
3. Дифракция Фраунгофера на одномерной дифракционной решетке. Многолучевая интерференция*.
4. Понятие о голографии.
Вопросы для самоконтроля.
1. Какое явление называется дифракцией?
2. Сформулируйте принцип Гюйгенса-Френеля.
3. Что такое зона Френеля?
4. Как объяснить образование максимумов и минимумов с помощью принципа Гюйгенса-Френеля?
5. Как отличается дифракция Фраунгофера от дифракции Френеля?
6. Как объясняется появление «пятна Пуассона»?
7. Выведите формулу распределения интенсивности при дифракции Фраунгофера на одномерной щели.
8. Что представляет собой дифракционная решетка? Каково распределение интенсивности на экране за дифракционной решеткой? Как оно объясняется?
9. Каков принцип голографии? Каковы возможные применения голографии?
Лекция № 34
ПОЛЯРИЗАЦИЯ СВЕТА
План
1. Естественный и поляризованный свет. Виды поляризации. Степень поляризации.
2. Поляризация при отражении и преломлении. Закон Брюстера.
3. Поляризация при двойном лучепреломлении. Обыкновенный и необыкновенный лучи. Оптическая ось кристалла. Волновые поверхности в одноосном кристалле.
4. Поляроиды и поляризационные предметы. Поляризаторы и анализаторы. Закон Малюса.
5. Искусственная оптическая анизотропия. Эффект Керра.
6. Вращение плоскости поляризации.
1. Естественный и поляризованный свет. Виды поляризации. Степень поляризации.
В естественном свете имеются колебания, совершающиеся в самых различных направлениях, перпендикулярных к лучу. Излучение светящегося тела слагается из волн, испускаемых его атомами. Процесс излучения отдельного атома продолжается около 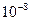 с. За это время успевает образоваться последовательность горбов и впадин (или, как говорят, цуг волн) протяженностью примерно 3 м. Одновременно излучает множество атомов. Цуги волн, испускаемых атомами, накладываются друг на друга, образуя испускаемую телом световую волну. Плоскость колебаний для вектора
с. За это время успевает образоваться последовательность горбов и впадин (или, как говорят, цуг волн) протяженностью примерно 3 м. Одновременно излучает множество атомов. Цуги волн, испускаемых атомами, накладываются друг на друга, образуя испускаемую телом световую волну. Плоскость колебаний для вектора 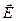 напряженности электрического поля у каждого цуга ориентирована случайным образом. Поэтому в результирующей волне колебания различных направлений представлены с равной вероятностью. Свет со всеми возможными равновероятными ориентациями вектора
напряженности электрического поля у каждого цуга ориентирована случайным образом. Поэтому в результирующей волне колебания различных направлений представлены с равной вероятностью. Свет со всеми возможными равновероятными ориентациями вектора  называется естественным. (Заметим, что вектор
называется естественным. (Заметим, что вектор 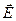 называется световым вектором, так как при действии света на вещество основное значение имеет электрическая составляющая поля волны, действующая на электроны в атомах вещества.)
называется световым вектором, так как при действии света на вещество основное значение имеет электрическая составляющая поля волны, действующая на электроны в атомах вещества.)
 Свет. в котором направление колебаний вектора упорядоченно каким либо образом, называется поляризованным.
Свет. в котором направление колебаний вектора упорядоченно каким либо образом, называется поляризованным.
Виды поляризации.
1. Если колебания вектора 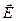 происходят только в одной плоскости, проходящей через луч, то свет называется плоскополяризованным (или линейнополяризованным). Плоскость, в которой колеблется вектор
происходят только в одной плоскости, проходящей через луч, то свет называется плоскополяризованным (или линейнополяризованным). Плоскость, в которой колеблется вектор 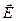 называется плоскостью поляризации (или плоскостью колебаний).
называется плоскостью поляризации (или плоскостью колебаний).
2. Если вектор  вращается по мере распространения волны в пространстве, а конец этого вектора в каждой точке пространства описывает окружность, то свет называется поляризованным по кругу (или циркулярно поляризованным).
вращается по мере распространения волны в пространстве, а конец этого вектора в каждой точке пространства описывает окружность, то свет называется поляризованным по кругу (или циркулярно поляризованным).
3. Если вектор  вращается вокруг направления распространения волны (вокруг луча), изменяясь периодически по модулю, при этом вектор
вращается вокруг направления распространения волны (вокруг луча), изменяясь периодически по модулю, при этом вектор  описывает эллипс, то свет называется эллиптически поляризованным.
описывает эллипс, то свет называется эллиптически поляризованным.
Если смотреть навстречу распространения волны и вектор  при этом поворачивается по часовой стрелке, то поляризация называется правой, если против часовой стрелки – левой.
при этом поворачивается по часовой стрелке, то поляризация называется правой, если против часовой стрелки – левой.
4. Если свет представляет смесь естественного и плоскополяризованного, то он называется частично поляризованным.
|
(34-1)
где  - максимальная и минимальная интенсивности света, соответствующие двум взаимно перпендикулярным компонентам вектора
- максимальная и минимальная интенсивности света, соответствующие двум взаимно перпендикулярным компонентам вектора 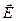 . Для плоскополяризованного света
. Для плоскополяризованного света 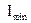 = 0 и р = 1; для естественного света
= 0 и р = 1; для естественного света 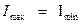 , соответственно р = 0; для эллиптически поляризованного света это понятие не применяется.
, соответственно р = 0; для эллиптически поляризованного света это понятие не применяется.
Вопросы для самоконтроля.
1. Чем отличается поляризованный свет от естественного? Каковы виды поляризованного света?
2. В чем смысл закона Брюстера?
3. В чем суть двойного лучепреломления? В чем особенности обыкновенного и необыкновенного лучей? Как объяснить двойное лучепреломление?
4. Что такое оптическая ось кристалла?
5. Объясните закон Малюса для света, прошедшего через два поляризатора.
6. Объясните эффект Керра.
7. С чем связано вращение плоскости поляризации на макро- и микроуровнях? Где применяется?
Лекция № 35
Вопросы для самоконтроля.
1. В чем заключается дисперсия света?
2. Какая дисперсия называется нормальной? Аномальной?
3. В чем суть метода скрещенных призм?
4. В чем суть электронной теории дисперсии? Выведите формулу зависимости n(ω).
5. Каковы затруднения электромагнитной теории Максвелла?
6. Напишите формулу закона Бугера и объясните ее.
7. Что такое спектр поглощения?
8. Как можно физически объяснить поглощение света в металлах?
9. Как цвета тел связаны с их спектрами поглощения?
Лекция №36 (дополнительная)
Вопросы для самоконтроля.
1. Что называется спектром функции? Спектрограммой?
2. Какова суть разложения Фурье?
3. Решите самостоятельно задачу о спектральном разложении несинусоидального периодического сигнала.
УРАВНЕНИЯ МАКСВЕЛА. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
План
1. Фарадеевская и максвелловская трактовки явления электромагнитной индукции. Ток смещения.
2. Система уравнений Максвелла в интегральной и дифференциальной формах. Электромагнитное поле.
3. Волновые уравнения для электромагнитного поля и их решения. Скорость распространения электромагнитных волн в средах. Основные свойства электромагнитных волн.
4. Энергия и поток энергии электромагнитных волн. Вектор Пойнтинга.
5. Изучение диполя. Диаграмма направленности.
1. Фарадеевская и максвелловская трактовки явления электромагнитной индукции. Ток смещения.
Из закона электромагнитной индукции Фарадея следует
ℇ  = -dФ/dt,
= -dФ/dt,
где ℇ  - ЭДС электромагнитной индукции; dФ/dt, - скорость изменения магнитного потока. В фарадеевской трактовке при изменении магнитного потока, пронизывающего некоторый проводящий контур, в нем возникает ЭДС и индукционный ток. Максвелл предположил, что изменяющееся со временем магнитное поле обуславливает появление в пространстве электрического поля независимо от присутствия в этом пространстве проволочного контура. Наличие контура лишь позволяет обнаружить по возникновению в нем индукционного тока существование в соответствующих точках пространства электрического поля.
- ЭДС электромагнитной индукции; dФ/dt, - скорость изменения магнитного потока. В фарадеевской трактовке при изменении магнитного потока, пронизывающего некоторый проводящий контур, в нем возникает ЭДС и индукционный ток. Максвелл предположил, что изменяющееся со временем магнитное поле обуславливает появление в пространстве электрического поля независимо от присутствия в этом пространстве проволочного контура. Наличие контура лишь позволяет обнаружить по возникновению в нем индукционного тока существование в соответствующих точках пространства электрического поля.
Итак, согласно идее Максвелла изменяющееся со временем магнитное поле порождает электрическое поле. Это поле существенно отличается от порождаемого неподвижными зарядами электростатического поля. Электростатическое поле потенциально, его силовые линии начинаются и заканчиваются на зарядах. Электрическое поле, создаваемое переменным магнитным полем вихревое, его силовые линии замкнуты.
В 1865 г. Максвелл высказал гипотезу о том, что изменение электрического поля должно вызывать образование магнитного поля. В дальнейшем эта гипотеза нашла экспериментальное подтверждение.
Переменное электрическое поле, которое может создавать переменное магнитное поле, Максвелл назвал током смещения.
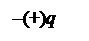
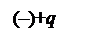 Рассмотрим цепь переменного тока, содержащую конденсатор (рис.
Рассмотрим цепь переменного тока, содержащую конденсатор (рис.
 30.1). Между обкладками заряжающегося и разряжающегося конденса-
30.1). Между обкладками заряжающегося и разряжающегося конденса-

Рис. 30.1 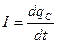 (30-1)
(30-1)
Так как 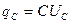 (С - емкость конденсатора,
(С - емкость конденсатора, 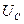 - напряжение на нем)
- напряжение на нем)
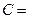 ℰℰ
ℰℰ 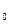 S/ℓ (здесь кроме известных обозначений ℓ - расстояние ме- жду пластинами конденсатора)
S/ℓ (здесь кроме известных обозначений ℓ - расстояние ме- жду пластинами конденсатора)
Напряжение на конденсаторе 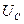 можно представить как произведение напряженности электрического поля внутри конденсатора на расстояние между пластинами, то есть
можно представить как произведение напряженности электрического поля внутри конденсатора на расстояние между пластинами, то есть 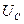 = Е ⋅ℓ, подставляя в (30 -1), получим
= Е ⋅ℓ, подставляя в (30 -1), получим
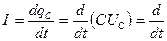 (Еℓ⋅ℰℰ
(Еℓ⋅ℰℰ 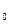 S/ℓ) = S⋅d(ℰℰ
S/ℓ) = S⋅d(ℰℰ 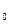 E)/ dt
E)/ dt
Выражение в скобках ℰℰ 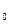 E = D – электрическое смещение, то есть
E = D – электрическое смещение, то есть
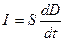
Разделим обе части на S, тогда в левой части будет плотность тока 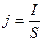 , а в правой -
, а в правой - 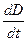 , то есть
, то есть 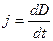 . Так как в общем случае
. Так как в общем случае 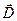 может иметь производные по координатам, запишем j через частную производную по времени
может иметь производные по координатам, запишем j через частную производную по времени 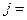
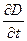 или в векторной форме
или в векторной форме
|
Эта величина получила название плотности тока смещения. Ток смещения находится интегрированием.






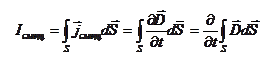
(30-2)
При этом еще раз отметим, что никакого тока между пластинами конденсатора нет, а есть переменное электрическое поле. Название «ток смещения» является условным, исторически сложившемся (так назвал Максвелл).
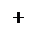






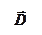
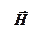












 По Максвеллу переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между
По Максвеллу переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между

т.е. вектор 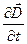 направлен противоположно вектору
направлен противоположно вектору 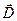 , а вектор
, а вектор 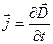 имеет такое направление, что как бы «продолжает» направление тока в подводящих проводах.
имеет такое направление, что как бы «продолжает» направление тока в подводящих проводах.
Максвелл ввел понятие полного тока, равного сумме токов проводимости и смещения. Плотность полного тока
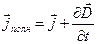 (30-3)
(30-3)
2. Система уравнений Максвелла в интегральной и дифференциальной формах. Электромагнитное поле.
В законе электромагнитной индукции (ЭМИ) ℇ  = -dФ/dt ЭДС можно представить по определению как циркуляцию поля сторонних сил
= -dФ/dt ЭДС можно представить по определению как циркуляцию поля сторонних сил
ℇ = 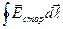 (см. часть 2, лекция №20), в данном случае (ЭМИ) сторонние силы не связаны ни с химическими, ни с тепловыми процессами, они также не могут быть магнитными силами, по тому, что такие силы работу над зарядами не совершают. Остается заключить, что индукционный ток обусловлен возникающим в проводе электрическим полем, тогда ЭДС
(см. часть 2, лекция №20), в данном случае (ЭМИ) сторонние силы не связаны ни с химическими, ни с тепловыми процессами, они также не могут быть магнитными силами, по тому, что такие силы работу над зарядами не совершают. Остается заключить, что индукционный ток обусловлен возникающим в проводе электрическим полем, тогда ЭДС
|
 =
= 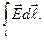 Магнитный поток по определению Ф =
Магнитный поток по определению Ф = 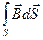 . Подставляя в закон ЭМИ получим
. Подставляя в закон ЭМИ получим
(30-4)
Это первое уравнение Максвелла.

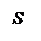
 Интеграл в правой части берется по произвольной поверхности S, опирающейся на контур ℓ (рис. 30.3).
Интеграл в правой части берется по произвольной поверхности S, опирающейся на контур ℓ (рис. 30.3).

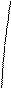
 (Поскольку в общем случае
(Поскольку в общем случае 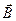 может быть
может быть
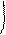
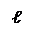
 функцией и координат, то берем частную
функцией и координат, то берем частную
производную 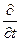 )
)
Смысл первого уравнения соответствует
максвелловской трактовке явления ЭМИ, то
есть, изменяющееся со временем магнитное поле порождает вихревое электрическое поле.
Второе уравнение Максвелла
|
(30-5)
Это уравнение выражает тот факт, что силовые линии магнитного поля не имеют источника (нет «магнитных зарядов») и всегда замкнуты и, что оно имеет вихревой характер, поток вектора магнитной индукции равен нулю.
Третье уравнение Максвелла
|
(30-6)
Это обобщенный закон полного тока (см. часть 3, лекция №24), который подчеркивает тот факт, что магнитное поле может создаваться не только токами проводимости ( 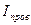 ), но и перемещенным электрическим полем («ток смещения»
), но и перемещенным электрическим полем («ток смещения» 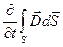 ).
).
Четвертая теорема Максвелла (см. часть 3, лекция №18).
|
(30-7)
Физически эта теорема подчеркивает тот факт, что электрическое поле может создаваться зарядами, то есть источниками силовых линий электрического поля являются электрические заряды.
Уравнения (30-3,5,6,7) представляют уравнения Максвелла в интегральной форме.
Уравнения Максвелла подчеркивают тот факт, что электрическое поле может создаваться как зарядами, так и переменным магнитным полем, а магнитное поле может создаваться как токами проводимости, так и переменным электрическим полем. При этом магнитное поле всегда носит вихревой характер, о чем говорит второе уравнение Максвелла. Электрическое поле, создаваемое зарядами и переменным магнитным полем носят различный характер.Силовые линии в первом случае начинаются и кончаются на зарядах (четвертое уравнение Максвелла). А электрическое поле, создаваемое переменным магнитным полем не имеет источников и носит вихревой характер, также как магнитное поле (первое уравнение Максвелла).
В вакууме, где нет зарядов и токов, магнитное поле может создаваться только переменным электрическим полем, а электрическое поле только переменным магнитным полем.
Эту совокупность непрерывно изменяющихся и порождающих друг друга электрического и магнитного полей Максвелл назвал электромагнитным полем.
Кроме четырех рассмотренных уравнений в полную систему уравнений Максвелла входят еще три уравнения, называемых материальными. В них входят характеристики вещества («материи»), такие как диэлектрическая и магнитная проницаемости ℰ и µ, проводимость σ.
|
Связь 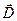 и
и 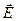 (лекция №18, часть 3)
(лекция №18, часть 3)
|
Связь 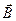 и
и 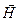 (лекция №23, часть 3)
(лекция №23, часть 3)
|
Закон Ома в локальной форме (лекция №20, часть 3)
Уравнения Максвелла (30-4) ÷ (30-7) можно представить в дифференциальной форме, т.е. в виде системы дифференциальных уравнений. Для этого используем теоремы Стокса
|
(30-8)
и Остроградского – Гаусса:
|
где 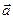 - некоторый вектор в нашем случае:
- некоторый вектор в нашем случае: 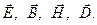 (О функции rot
(О функции rot 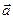 см. примечание к п.2).
см. примечание к п.2).
Первое уравнение Максвелла
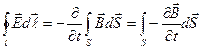
С другой стороны, используя теорему Стокса, получим
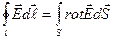
Поскольку равны левые части, равны и правые
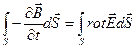
откуда следует
|
(30-10)
Второе уравнение Максвелла
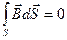
С другой стороны из теоремы Остроградского – Гаусса
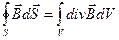
|
Третье уравнение запишем, предварительно выразив токи проводимости через плотность токов проводимости 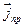
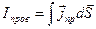 ,
,
тогда
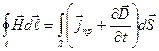
с другой стороны
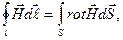
получим
|
(30-12)
Аналогичный подход для четвертого уравнения дает систему уравнений
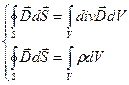 ,
,
|
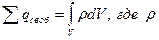 - объемная плотность заряда) из которой следует:
- объемная плотность заряда) из которой следует:
(30-13)
Сведем четыре уравнения Максвелла в интегральной и дифференциальной формах, а также три материальных уравнения в таблицу:
Уравнения Максвелла
| Интегральная форма | Дифференциальная форма |
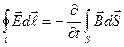
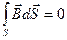
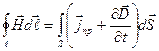
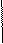 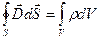
| 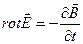
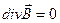
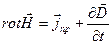
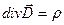

|
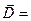 ℰℰ
ℰℰ 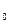
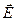 ;
; 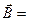 μμ
μμ 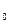
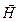 ;
; 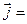 σ
σ 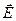
Отметим, что физический смысл уравнений в дифференциальной форме такой же, что и соответствующих уравнений в интегральной форме. Интегрируя их, можно получить 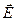 ,
, 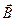 ,
, 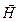 ,
, 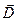 .
.
Примечание.Вихревое электрическое поле характеризуется особой векторной величиной, называемой ротором напряженности поля: 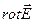 . Вектор ротора приложен в центре поля перпендикулярно плоскости его силовых линий (в случае круговых линий – в центре окружностей) и направлен относительно них согласно правилу правого винта.
. Вектор ротора приложен в центре поля перпендикулярно плоскости его силовых линий (в случае круговых линий – в центре окружностей) и направлен относительно них согласно правилу правого винта.
По определению
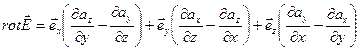 .
.
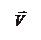








 Наглядное представление о роторе вектора можно получить, представив себе небольшую легкую турбинку, помещенную в данную точку текущей жидкости.
Наглядное представление о роторе вектора можно получить, представив себе небольшую легкую турбинку, помещенную в данную точку текущей жидкости.


 |
3. Волновые уравнения для электромагнитного поля и их решения. Скорость распространения электромагнитных волн в средах. Основные свойства электромагнитных волн.
Пусть имеется однородная и изотропная среда вдали от зарядов и токов. Возбудим в какой-либо точке пространства переменное электрическое гармоническое поле 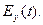 (Предположим
(Предположим 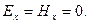 Для простоты рассматриваем этот частный случай).
Для простоты рассматриваем этот частный случай).
Из уравнений Максвелла при условии сделанных предположений можно получить волновые уравнения электромагнитного поля


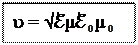
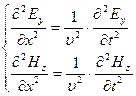 , (30-14)
, (30-14)
где - скорость распространения электро-
магнитной волны.
Процесс распространения электромагнитного поля в пространстве называется электромагнитной волной.
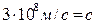 Подставим ℰ
Подставим ℰ 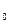 = 8,85
= 8,85 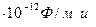 μ
μ 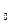 =
= 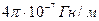 в выражение для скорости u. Если среда – вакуум, то ℰ = 1, μ = 1, тогда получим u = , то есть скорость электромагнитной волны в вакууме равна скорости света в вакууме. Это обстоятельство приводит к выводу, что свет - электромагнитная волна.
в выражение для скорости u. Если среда – вакуум, то ℰ = 1, μ = 1, тогда получим u = , то есть скорость электромагнитной волны в вакууме равна скорости света в вакууме. Это обстоятельство приводит к выводу, что свет - электромагнитная волна.
Решения уравнений (30-14)
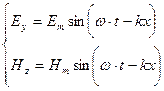 (30-15)
(30-15)
Выражения (30-15) – уравнения электромагнитной волны. Их графическое


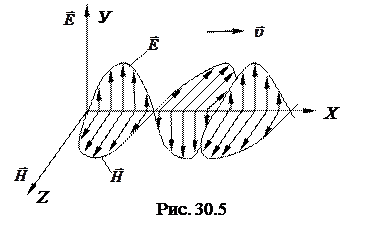
Как показывает опыт, электромагнитные волны проходят через диэлектрики и отражаются от металлов. Для них свойственны такие явления как интерференция, дифракция, поляризация, дисперсия (рассмотрим далее в разделе «Оптика»).
Итак, из решения уравнений Максвелла получаются следующие выводы:
– если в какой-либо ограниченной области пространства возникает электромагнитное поле, то оно не остается локализованным в этой области, а распространяется с конечной скоростью, зависящей от свойств среды;
– если электрическое и магнитные поля меняются по простому гармоническому закону, то электромагнитное поле распространяется в пространстве в виде плоской электромагнитной волны.
4. Энергия и поток энергии электромагнитных волн. Вектор Пойнтинга.
Поскольку и электрическое и магнитное поля обладают определенной энергией, то электромагнитная волна имеет определенный запас энергии. Объемная плотность электрического поля 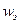 = ℰℰ
= ℰℰ 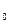
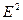 /2, магнитного поля
/2, магнитного поля 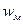 = μμ
= μμ 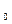
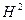 /2. Можно показать [ ], что вследствие равноценности электрического и магнитного полей
/2. Можно показать [ ], что вследствие равноценности электрического и магнитного полей 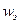 =
= 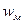 . То есть
. То есть
ℰℰ 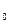
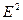 /2= μμ
/2= μμ 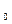
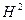 /2.
/2.
Извлекая, квадратный корень из обеих частей, получим


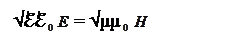
 (30-16)
(30-16)
 Существенно то, что электрическое и магнитное поля колеблются в одинаковых фазах. Они одновременно достигают максимума и минимума, но в двух взаимно перпендикулярных плоскостях.
Существенно то, что электрическое и магнитное поля колеблются в одинаковых фазах. Они одновременно достигают максимума и минимума, но в двух взаимно перпендикулярных плоскостях.
Плотность энергии электромагнитного поля складывается из составляющих
w = 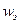 +
+ 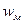 = ℰℰ
= ℰℰ 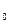
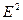 /2 + = μμ
/2 + = μμ 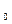
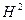 /2
/2
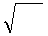 |
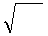
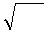
Представляя ℰℰ 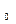 ∙
∙ 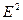 /2 как ℰℰ
/2 как ℰℰ 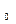 ∙
∙ 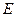 ∙ ℰℰ
∙ ℰℰ 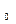 ∙
∙ 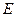 /2 и μμ
/2 и μμ 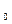 ∙
∙ 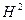 /2 как μμ
/2 как μμ 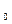 ∙
∙ 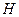 ∙
∙
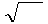 μμ
μμ 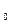 ∙
∙ 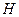 /2, получим
/2, получим
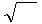
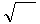
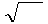
 w = ℰℰ
w = ℰℰ 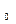 ∙
∙ 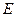 ∙ ℰℰ
∙ ℰℰ 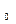 ∙
∙ 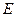 /2 + μμ
/2 + μμ 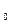 ∙
∙ 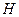 ∙ μμ
∙ μμ 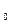 ∙
∙ 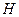 /2
/2
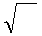

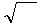 Умножим и разделим первое слагаемое на μμ
Умножим и разделим первое слагаемое на μμ 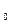 ∙
∙ 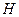 , а второе на ℰℰ
, а второе на ℰℰ 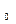 ∙
∙ 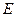
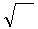
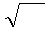
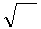
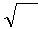
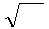 w = μμ
w = μμ 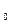 ∙
∙ 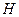 ℰℰ
ℰℰ 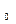 ∙
∙ 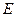 /2 ∙ ℰℰ
/2 ∙ ℰℰ 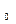 ∙
∙ 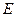
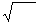

 / μμ
/ μμ 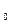 ∙
∙ 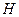
 + ℰℰ
+ ℰℰ 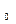 ∙
∙ 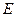 μμ
μμ 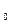
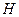 /2∙
/2∙
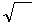
 ∙ μμ
∙ μμ 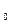 ∙
∙ 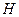 / ℰℰ
/ ℰℰ 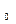 ∙
∙ 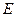
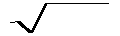 Учитывая равенство (30-16), производим необходимые сокращения и в результате получим
Учитывая равенство (30-16), производим необходимые сокращения и в результате получим
w = ℰ∙ℰ 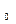 ∙μ∙μ
∙μ∙μ 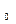 ∙
∙ 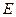 ∙
∙ 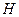
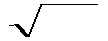 Поскольку 1/ ℰ∙μ∙ℰ
Поскольку 1/ ℰ∙μ∙ℰ 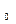 ∙μ
∙μ 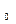 = u - скорость распространения электромагнитной волны (см. (30-15)), то w = 1/ u ∙
= u - скорость распространения электромагнитной волны (см. (30-15)), то w = 1/ u ∙ 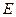
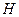 . Умножив найденное выражение для w на скорость волны u, получим модуль вектора плотности потока энергии S = w∙ u =
. Умножив найденное выражение для w на скорость волны u, получим модуль вектора плотности потока энергии S = w∙ u = 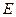 ∙
∙ 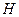 . Векторы
. Векторы 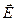 и
и 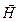 перпендикулярны и образуют с направлением распространения волны правовинтовую систему. Следовательно, вектор плотности потока электромагнитной энергии можно представить как векторное произведение
перпендикулярны и образуют с направлением распространения волны правовинтовую систему. Следовательно, вектор плотности потока электромагнитной энергии можно представить как векторное произведение 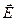 и
и 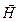 , так как направление вектора
, так как направление вектора 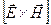 совпадает с направлением переноса энергии, а модуль этого вектора равен
совпадает с направлением переноса энергии, а модуль этого вектора равен 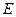
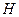 . Таким образом
. Таким образом
|
(30-17)
Вектор 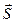 называется вектором Пойнтинга. (Или вектором Умова-Пойнтинга.) Общее представление о потоке энергии в пространстве впервые было введено русским ученым Умовым в 1874 г. Поэтому вектор потока энергии без конкретизации ее физической природы называется вектором Умова. Пойнтингом было получено выражение (30-17).)
называется вектором Пойнтинга. (Или вектором Умова-Пойнтинга.) Общее представление о потоке энергии в пространстве впервые было введено русским ученым Умовым в 1874 г. Поэтому вектор потока энергии без конкретизации ее физической природы называется вектором Умова. Пойнтингом было получено выражение (30-17).)
Физический смысл вектора Пойнтинга – плотность потока электромагнитной энергии, распространяющейся вместе с волной, то есть количество энергии, проходящей за единицу времени через единицу площади, расположенной перпендикулярно к направлению распространения волны (рис. 30.6).
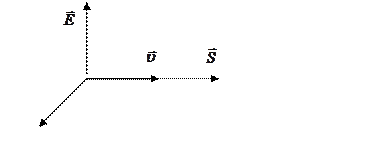
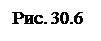
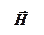
5. Изучение диполя. Диаграмма направленности.
Простейшим излучателем электромагнитных волн является электрический диполь, электрический момент которого изменяется во времени по гармоническому закону 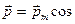 ωt, где
ωt, где 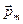 - амплитуда вектора
- амплитуда вектора 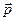 . Примером подобного диполя может служить система, состоящая из покоящегося заряда +Q и отрицательного заряда – Q, гармонически колеблющегося вдоль направления
. Примером подобного диполя может служить система, состоящая из покоящегося заряда +Q и отрицательного заряда – Q, гармонически колеблющегося вдоль направления 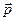 с частотой ω.
с частотой ω.
Задача об излучении диполя имеет в теории излучающих систем важное значение, так как всякую реальную излучающую систему (например, антенну) можно рассчитывать, рассматривая излучение диполя. Кроме того, многие вопросы взаимодействия излучения с веществом можно объяснить на основе классической теории, рассматривая атомы как системы зарядов, в которых электроны совершают гармонические колебания около их положения равновесия.
Характер электромагнитного поля диполя зависит от выбора рассматриваемой точки. Особый интерес представляет так называемая волновая зона диполя – точки пространства, отстоящие от диполя на расстоянии r, значительно превышающего длину волны (r>>λ), так как в ней картина электромагнитного поля диполя сильно упрощается. Это связано с тем, что в волновой зоне диполя практически остаются только «отпочковавшиеся» от диполя, свободно распространяющиеся поля, в то время как поля, колеблющиеся вместе с диполем и имеющие более сложную структуру, сосредоточены в области расстояний r<<λ. (Заметим, что в этой области справедливы те же формулы, что и для постоянных электрического и магнитного полей.)
В волновой зоне векторы 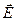 и
и 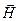 колеблются по закону cos(ωt –kr). Амплитуды этих векторов зависят от расстояния r до излучателя и угла ϑ между направлением радиуса-вектора и осью диполя и пропорциональны
колеблются по закону cos(ωt –kr). Амплитуды этих векторов зависят от расстояния r до излучателя и угла ϑ между направлением радиуса-вектора и осью диполя и пропорциональны 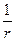 sinϑ. Отсюда следует, что интенсивность излучения диполя в волновой зоне
sinϑ. Отсюда следует, что интенсивность излучения диполя в волновой зоне 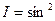 ϑ/
ϑ/ 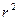 .
.
 Зависимость от ϑ при заданном значении r, приводимая в полярных координатах, называется диаграммой направленности излучения диполя (см. рис. 30.7).
Зависимость от ϑ при заданном значении r, приводимая в полярных координатах, называется диаграммой направленности излучения диполя (см. рис. 30.7).

Вопросы для самоконтроля .
1. В чем заключается максвелловская трактовка явления электромагнитной индукции?
2. Что называется током смещения?
3. Напишите систему уравнений Максвелла в интегральной и дифференциальной формах. В чем состоит физический смысл каждого уравнения?
4. Напишите волновые уравнения для электромагнитного поля и их решения.
5. Перечислите Основные свойства электромагнитных волн.
6. Что называется вектором Пойнтинга? Каков его физический смысл?
7. нарисуйте диаграмму направленности излучения диполя.
ОПТИКА
Лекция № 31
Дата: 2019-02-02, просмотров: 368.
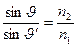
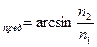
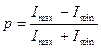
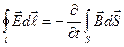
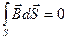
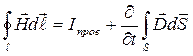
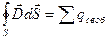
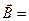 μμ
μμ 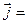 σ
σ