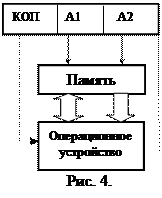
Рассмотрим особенности выполнения команд с сокращенным количеством адресных полей на примере двухадресных команд, достаточно широко применяемых в современных ЭВМ. Состав полей двухадресной команды приведен на Рис.4.
Исключение поля АСК компенсируется включением в состав устройства управления специализированного регистра – счетчика команд (СК).
При запуске программы в счетчик заносится адрес первой команды программы. После считывания команды из памяти значение счетчика увеличивается на ее длину. Таким образом, в счетчике окажется адрес следующей по порядку команды.
Такой прием позволяет выполнять команды в порядке их записи в программе. Такой порядок выполнения команд называют естественным порядком.
Для изменения естественного порядка команд в программу включаются специальные команды управления, которые принудительно изменяют текущее состояние счетчика путем занесения в него адреса перехода, т.е. адреса команды, которая должна быть выполнена следующей. После выполнения перехода естественный порядок выполнения программы возобновляется.
Исключение поля A3 компенсируется за счет записи результата по адресу одного из операндов, чаще всего первого. Формализованной записью схемы выполнения двухадресной команды будут выражения:
1. A1 Ü (A1) Ä (A2)
2. СК Ü (СК) + Lк,
где Lк – длина выполняемой команды;
знак Ü обозначает запись по указанному слева от знака адресу данных, указанных справа от знака;
знак Ä обозначает операцию, которую необходимо выполнить.
Адрес, заключенный в круглые скобки, означает чтение данных, другими словами – содержимое ячейки памяти или регистра.
Если первый операнд нужен для дальнейших вычислений, придется выполнить предварительное копирование первого операнда в рабочую ячейку памяти или регистр общего назначения. Обозначим адрес этой ячейки как AS. Т.о. придется выполнить следующие действия:
1. AS Ü (A1)
2. A1 Ü (A1) Ä (A2).
3. СК Ü (СК) + Lк
Понятие способа адресации
Способ адресации – это правила записи в команде логического адреса и правила вычисления на его основе исполнительного адреса. Применение того или иного способа адресации во многом зависит от требований к размещению программы в основной памяти.
Специализированные ЭВМ имеют фиксированный набор программ. Размещение программ в основной памяти можно спланировать заранее. Основной целью кодирования адресов является сокращение длины команды.
Набор программ для ЭВМ общего назначения заранее не известен. Предварительно спланировать размещение программ в памяти невозможно. Кодирование адресов должно обеспечить размещение программы в любом месте памяти без внесения изменений в программу. Это свойство называют перемещаемостью программы. Другими словами, изменение результата вычисления АИ=F(АЛ) должно достигаться без изменения логического адреса.
Дадим краткое описание наиболее используемых способов адресации.
Прямая адресация. В команде указывается исполнительный адрес. Правило декодирования: АИ = АЛ. Время вычисления исполнительного адреса минимально. Перемещаемость программ не поддерживается. Длина логического адреса максимальна. Применяется для адресации данных в регистрах общего назначения
Косвенная адресация. В команде указывается адрес, по которому хранится исполнительный адрес. Правило декодирования: АИ = (АЛ). Поддерживается перемещаемость программ. При хранении исполнительного адреса в основной памяти длина логического адреса максимальна. Для получения исполнительного адреса необходимо дополнительное обращение в память. При хранении исполнительного адреса в регистре общего назначения сокращается длина логического адреса и время получения исполнительного адреса.
Относительная адресация
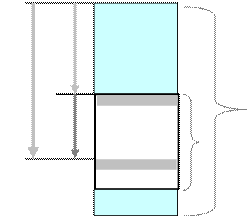Относительная адресация в различных вариантах реализации является основной в ЭВМ общего значения и изначально ориентирована на поддержку перемещаемости программ. Суть относительной адресации показана на рисунке 5.
При составлении каждой программы отсчет логических адресов производится с нуля. При размещении программы в выделенной ей памяти для программы назначается база. База представляет собой исполнительный адрес начала выделенной области памяти.
При вычислении исполнительного адреса логический адрес рассматривается как смещение D от базы АИ = База + D.
Рис.5.
Изменение базы при неизменных логических адресах в командах позволяет “привязать” программу к любому месту основной памяти.
Обычно значение базы устанавливается при загрузке программы в основную память и хранится либо в специальном программно недоступном регистре или одном из регистров общего назначения.
Разновидностью относительной адресации является индексная адресация:
АИ = База + Индекс + D.
Значение индекса хранится в специальном регистре индекса или одном из регистров общего назначения. Индекс позволяет обрабатывать данные в последовательно расположенных ячейках памяти без изменения команды. Для изменения исполнительного адреса достаточно изменить значение индекса.
Непосредственная адресация
Операнд записывается непосредственно в команде на месте логического адреса. Декодирование логического адреса не требуется, так как Операнд=АЛ. Непосредственная адресация применяется для записи констант.
КОДЫ ДВОИЧНЫХ ЧИСЕЛ
- Разрядная сетка
Все данные в центральной части ЭВМ хранятся и обрабатываются в виде двоичных кодов. Для размещения кода отводится строго фиксированное число двоичных разрядов, образующих разрядную сетку. Без привязки к разрядной сетке понятие кода не определено. Каждый разряд кода нумеруется, начиная с нуля. В разных ЭВМ принята разная система нумерации. В универсальных ЭВМ разряды нумеруются слева направо, а в мини и микро-ЭВМ – справа налево. Пример нумерации для n двоичных разрядов приведен ниже.
| Номера ß разрядов ß | a0 | a1 | a2 | … | an-2 | an-1 | Универсальные ЭВМ |
| 2n-1 2n-2 2n-3 ….. 21 20 | Вес разрядов | ||||||
| an-1 | an-2 | … | a2 | a1 | a0 | Мини и микро-ЭВМ | |
При любой системе нумерации левый разряд имеет наибольший вес, а правый – наименьший. Положение точки, отделяющей целую и дробную часть, подразумевается. В большинстве ЭВМ считается, что точка находится после младшего разряда. В этом случае в разрядной сетке размещаются коды целых чисел.
Наиболее просто кодируются целые числа без знака. В этом случае в разрядную сетку записывается двоичное представление числа. Каждая цифра числа занимает разряд в соответствии со своим весом.
Для кодирования целых чисел со знаком применяют:
· Прямой код.
· Обратный код.
· Дополнительный код.
Прямой код
Прямой n-разрядный двоичный код состоит из знакового разряда и
n-1 разрядов для записи модуля числа. В качестве знакового разряда используется старший разряд.
| an-1 | an-2 | ... | a0 |
Знак “плюс” кодируется как 0, а знак “минус” – как 1.
Определим диапазон чисел, представимых в прямом n-разрядном двоичном коде. Введем следующие обозначения: A+max – максимальное положительное число, A-min - минимальное отрицательное число:
A+max = 2n-1 – 1; A-min = -(2n-1-1)
Пример: Получить прямой 5-ти разрядный код числа A[10] = -6.Определить диапазон чисел для этой разрядной сетки.
1.| A[10] | = 6 Þ | A[2] | = 0110 (на запись модуля выделено 4 разряда)
2.Знаковый разряд = 1
|
Определим диапазон чисел:
A+max = 24 – 1 = 15 A-max = -(24 – 1) = -15
Пример: Получить прямой 8-ми разрядный код числа A[16] = 3С. Определить диапазон чисел для этой разрядной сетки.
1.| A[16] | = 3С Þ | A[2] | = 0111100 (на запись модуля выделено 7 разрядов)
2.Знаковый разряд = 0
|
Определим диапазон чисел:
A+max = 27 – 1 = 127 A-max = -(27 – 1) = -127
Прямой код для кодирования целых чисел со знаком в ЭВМ практически не применяется и используется как составная часть более сложных кодов.
Недостатки:
1. Сложение и вычитание чисел в прямом коде выполняется по правилам алгебры:
(С)пр = (А)пр + (В)пр
(С)пр = (А)пр - (В)пр ,
поэтому процессор должен иметь два разных устройства: сумматор и вычитатель.
2. Знаковый разряд обрабатывается отдельно от остальных по особым правилам.
3. Неоднозначность кодировки нуля:
|
|
Обратный код
Обратный код предполагает, что при кодировании числа и выполнении операций с кодами используются одинаковые правила обработки всех разрядов, включая знаковый. Обратный n-разрядный двоичный код – это код образованный по правилу:
 |
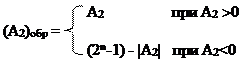Операция вида (2n – 1) - |A2| дает дополнение до наибольшего числа без знака, представимого в в n-разрядной сетке. Другими словами, кодирование числа можно выполнить следующим образом:
· Для положительного числа в n-разрядную сетку записывается его двоичное представление.
· Для отрицательного числа в n-разрядную сетку записывается разность между наибольшим числом без знака и модулем кодируемого числа.
В обоих случаях значение знакового разряда будет получено автоматически.
|
 |
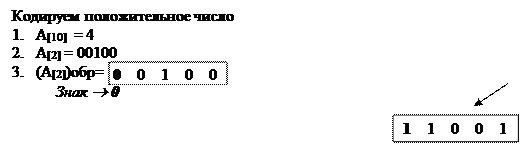Замечания:
v Операция дополнения для двоичного обратного кода эквивалентна инверсии всех разрядов. Инверсия удобна для реализации в операционном устройстве.
v Если длина разрядной сетки кратна 4, дополнение удобно вычислять в шестнадцатеричной системе счисления. Такая разрядная сетка характерна для большинства ЭВМ.
v Если длина разрядной сетки кратна 3, дополнение удобно вычислять в восьмеричной системе счисления. Такая разрядная сетка не характерна для ЭВМ. Однако для мини-ЭВМ с 16-ти разрядной сеткой при документировании программ часто пользуются восьмеричной записью кодов чисел, при этом старший разряд рассматривается как двоичная цифра.
Пример: Определить обратный код числа А[10] = -21 при n=16.
Получим обратный код во всех трех указанных формах. Так как кодируется отрицательное число, необходимо вычислить дополнение и использовать его в качестве обратного кода.
v Двоичное кодирование.
1. |А[10]| = 21
2. |А[2]| = 10101
3. |А[2]| = 0000 0000 0001 0101 (Это модуль кодируемого числа в разрядной сетке)
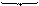
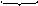
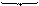
4. (А[2])обр= 1111 1111 1110 1010
F F E A[16]
v Шестнадцатеричное кодирование
1. | А[10]| = 21
|А[16]| = 15
2. (А[16])обр = F F F F (Это максимальное число без знака)
- 0 0 1 5 (Это модуль кодируемого числа в разрядной сетке)
F F E A
v Восьмеричное кодирование
1. | А[10]| = 21
|А[8]| = 25
2. (А[8])обр = 1 7 7 7 7 7 (Это максимальное число без знака)
- 0 0 0 0 2 5 (Это модуль кодируемого числа в разрядной сетке)
1 7 7 7 5 2
Диапазон чисел в обратном коде составляет: A+max = 2n-1 – 1; A-min = -(2n-1-1)
Достоинства:
1 Сложение и вычитание можно выполнять на одном устройстве: сумматоре, поскольку вычитание может быть заменено сложением с дополнением вычитаемого:
(С)обр = (А)обр + (В)обр
(С)обр = (А)обр - (В)обр = (А)обр + ((В)обр)обр
2 Знаковый разряд обрабатывается по общим правилам. Его значение при выполнении операции устанавливается автоматически.
Недостатки:
Неоднозначность кодировки нуля:
|
|
Чаще всего в ЭВМ используется модификация обратного кода – дополнительный код.
Дополнительный код
 |
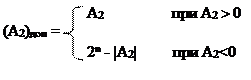Дополнительный код обладает всеми достоинствами обратного и устраняет его главный недостаток – неоднозначность кодирования нуля. Дополнительный n-разрядный двоичный код представляет собой код, образованный по правилу:
Операция 2n – |A2| называется операцией дополнения до следующего за большим числом без знака для данной разрядной сетки. Другими словами, кодирование числа можно выполнить следующим образом:
· Для положительного числа в n-разрядную сетку занести его двоичное представление.
· Для отрицательного числа в n-разрядную сетку занести разность между следующим
за большим числом без знака и модулем кодируемого числа.
Дополнение при использовании дополнительного кода больше по значению на 1 от дополнения при использовании обратного кода:
( 2n – 1 ) - |A2| + 1 = 2n - |A2|
 |
C ледствие: дополнительный код отрицательного числа может быть получен из его обратного кода путем прибавления единицы в младший разряд.
Пример: Определить дополнительный код числа А[16] = -1D8 при n=16.
Кодируется отрицательное число, следовательно, необходимо вычислить дополнение и использовать его в качестве кода.
v Двоичное кодирование.
1. |А[16]| = 1D8
2. |А[2]| = 111011000
3. |А[2]| = 0000 0001 1101 1000 (Это модуль кодируемого числа в разрядной сетке)
4. (А[2])обр= 1111 1110 0010 0111 (Это обратный код)
+ 1
(А[2])доп= 1111 1110 0010 1000 (Это дополнительный код)
F E 2 8 [16]
v Шестнадцатеричное кодирование
1. | А[16]| = 1D8
2. (А[16])обр F F F F (Это максимальное число без знака)
- 0 1 D 8 (Это модуль кодируемого числа в разрядной сетке)
F E 2 7 (Это обратный код)
+ 1
(А[16])доп= F E 2 8 (Это дополнительный код)
v Восьмеричное кодирование
1. | А[8]| = 730
2. (А[8])обр = 1 7 7 7 7 7 (Это максимальное число без знака)
- 0 0 0 7 3 0 (Это модуль кодируемого числа в разрядной сетке)
1 7 7 0 4 7 (Это обратный код)
+ 1
(А[8])доп= 1 7 7 0 5 0 (Это дополнительный код)
Дополнительный код обеспечивает однозначное представление нуля:
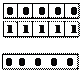+0 при n=5
-0 при n=5
+ 1
Диапазон представимых чисел в дополнительном коде: A+max = 2n-1 – 1; A-min = -2n-1
Дата: 2019-02-02, просмотров: 323.
