ЭВМ преобразует информацию, представленную в виде двоичных кодов. Каждый разряд кода принимает значение 0 или 1. Именно поэтому для описания функционирования устройств ЭВМ широко используется аппарат алгебры логики.
Алгебра логики изучает логические функции. Функция Y(x0,x1,…,xn) является логической, если ее аргументы и она сама принимают только одно из двух значений: “истина” или “ложь”. Значение “истина” принято кодировать как 1, а значение “ложь” - как 0.
Аргументы логической функции называют логическими переменными. В алгебре логики логические переменные принято обозначать строчными латинскими буквами, а функции – прописными латинскими буквами.
Часто логические переменные и функции называют булевыми от имени английского математика Джорджа Буля, занимавшегося разработкой основ алгебры логики.
Логические функции строятся на основе элементарных логических операций. Так как значение логических переменных и функций ограничено значениями 0 и 1, определение смысла логических операций удобно производить табличным способом. В таблице приводятся все комбинации значений переменных и результат операции. Таблицу такого рода в алгебре логики называют таблицей истинности. Приведем таблицы истинности для элементарных логических операций.
1. Логическое отрицание (НЕ, инверсия:` x
x ` x
0 1
1 0
2. Логическое умножение (И, конъюнкция): x1 Ù х2.
Иногда эта операция обозначается через знак умножения или его пропуск: х1·х2 или х1х 2.
| x1 | x2 | x1 Ù x2 |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
3. Логическое сложение (ИЛИ, дизъюнкция): x1 Ú x2.
Иногда эта операция обозначается через знак сложения: х1+х2.
| x1 | x2 | x1 Ú x2 |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Выражение, содержащее логические переменные и логические операции, называется логическим выражением. Порядок выполнения операций определяется их старшинством (приоритетом). Приоритет логических операций приведен на рисунке. Порядок выполнения операций можно регулировать скобками. Операции в скобках выполняются в первую очередь.
Подобно алгебраическим операциям, для логических операций существуют законы их выполнения, свойства и следствия из них.
Основные законы логических операций:
Переместительный закон: aÚb=bÚa; a·b=b·a
Сочетательный закон: aÚ(bÚc) = (aÚb)Úc = bÚ(aÚc)
a·(b·c) = (a·b) ·c = b·(a·c).
Распределительные законы: a·(bÚc) = a·bÚ a·с (первый)
aÚ(b·c) = (aÚb)·(aÚс) (второй)
Закон двойственности (закон де Моргана):
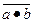= `a Ú`b
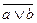= `a ·`b
Закон двойственного отрицания: `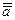 
= a 
Закон исключения: a Ú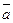 
= 1
Закон противоречия: a· 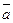= 0
Основные свойства логических операций:
Свойства логического умножения: 0·a = 0, 1·a = a
Свойства логического сложения: 0Úa = a, 1Úa = 1
Свойство повторения: a·a· a· … · a·a=a; aÚaÚaÚ … ÚaÚa=a.
Из перечисленных законов и свойств вытекает широко использующихся следствия:
C клеивание a · x Ú a ·`x = a · (x Ú`x) = a · 1 = a
(a Ú x) · (a Ú`x) = a Ú (x ·`x) = a · 0 = a
Неполное склеивание :
a · x Ú a ·`x Ú a = a · (x Ú`x Ú 1) = a · 1 = a
Поглощение : a Ú a · x = a · (1 Ú x) = a · 1 = a
a Ú a ·`x = a · (1 Ú`x) = a · 1 = a
a ·(a Ú x) = a·a Úa·x = aÚa·x = a·(1Úx) = a·1 = a
a ·(a Ú`x) = a·a Úa·`x = aÚa·`x = a·(1Ú`x) = a·1 = a
Устройства ЭВМ реализуют логические функции. Для сокращения элементов в устройстве логическую функцию максимально упрощают. Упрощение логической функции преследует цель сократить количество переменных и операций до минимума. Этот процесс называют минимизацией. Минимизация проводится на основе законов, свойств и следствий алгебры логики. Рассмотрим пример минимизации:
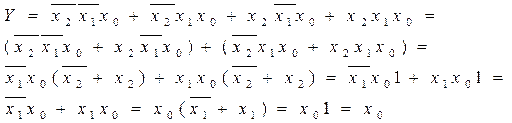
Дата: 2019-02-02, просмотров: 310.
