ЛЕКЦИЯ № 9
ЧЕРВЯЧНАЯ ПЕРЕДАЧА
Основные сведения. Классификация.
Червячные передачи применяют для передачи движения между перекрещивающимися осями. Угол перекрещивания может быть произвольным, но чаще используют угол равный 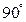 . По сравнению с зубчатыми передачами они дают возможность в больших пределах изменять угловые скорости. Червячная передача состоит из червяка, представляющего собой винт, и червячного колеса.
. По сравнению с зубчатыми передачами они дают возможность в больших пределах изменять угловые скорости. Червячная передача состоит из червяка, представляющего собой винт, и червячного колеса.
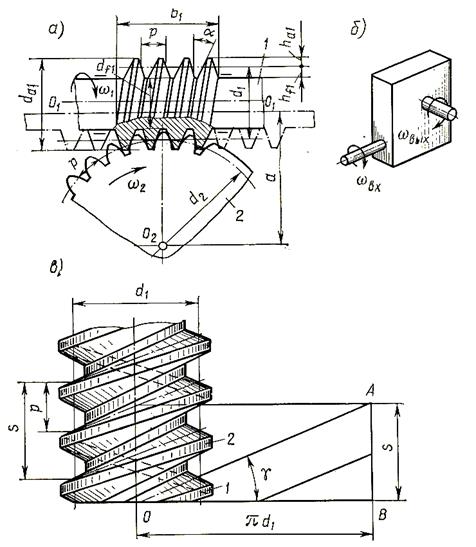
Обычно червячные передачи используют в качестве редукторов, когда движение передается от червяка к колесу, реже в мультипликаторах при обратной передаче (от колеса к червяку). В приборостроении применяются червячные передачи с эвольвентным профилем (даже в быстроходных механизмах при значительных нагрузках).
По форме поверхности, на которой образуется резьба, различают цилиндрические и глобоидные червяки (винт, нарезанный по поверхности тора).
В зависимости от формы профиля витка цилиндрических червяков различают:
- с архимедовым профилем (трапецеидальный в осевом сечении),
- с конволютным профилем (трапецеидальный в нормальном сечении),
- с эвольвентным профилем (в осевом сечении).
Передаточное отношение червячной передачи.
Передаточное отношение червячного механизма определяется числом зубьев колеса z 2 и числом заходов червяка z1. В червячной паре, в отличие от зубчатой передачи окружные скорости V1 и V2 не совпадают. Они направлены под углом 90о и различны по значению. Поэтому особенностью червячной передачи является то, что передаточное отношение не может быть выражено отношением 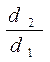 .
.
Запишем передаточное отношение через кинематические параметры:
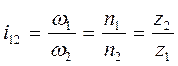 ,
,
или
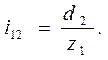
В редукторе при повороте однозаходного червяка на один оборот, червячное колесо поворачивается на один угловой шаг, при двухзаходном червяке – на два шага и т.д.
Это можно записать так:
Если 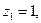 то
то 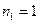 оборота;
оборота; 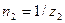 оборота;
оборота;
если 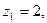 то
то 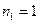 оборота;
оборота; 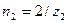 оборота;
оборота;
если 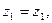 то
то 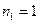 оборота;
оборота; 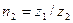 оборота.
оборота.
Усилия в зацеплении червячной передачи.
Рассмотрим случай, когда ведущим является червяк, а ведомым является колесо.
Считаем, что известны передаточные отношения и размеры. Необходимо определить момент М1 на валу червяка, необходимый для преодоления момента нагрузки М2 на валу колеса и сил трения.

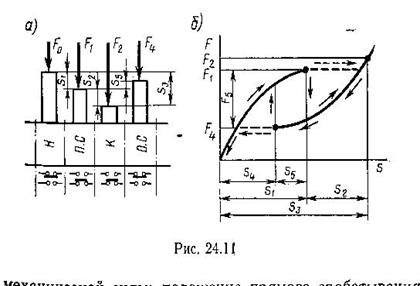
В соответствии с рис. F 1 , F 2 - окружные силы; Fr 1 , Fr 2 - радиальные силы;
Fa 1 , Fa 2 - осевые силы.
Запишем основные соотношения этих параметров:
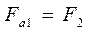 ;
; 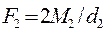 ;
; 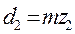 ;
;
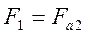 ;
; 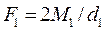 ;
; 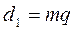 ;
;
 .
.
Определение соотношения моментов и коэффициента полезного действия передачи
Движение зуба колеса по витку червяка это перемещение по наклонной плоскости, расположенной под углом 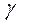 к горизонтали.
к горизонтали.
Лекция №10
Передача «винт-гайка»
Основные понятия
Передачи «винт-гайка» служат для преобразования вращательного движения в поступательное. Основными деталями этой передачи являются - винт (цилиндр с наружной резьбой) и гайка (кольцо с внутренней резьбой).
Эти передачи разделяют на силовые и кинематические (отсчетные). Силовые передачи должны иметь высокий КПД и высокую прочность, кинематические должны обеспечивать точность перемещения.
Существует два варианта применения передачи:
- ведущей деталью является винт, вращательное движение которого преобразуется в осевое при неподвижной гайке;
- ведущей деталью является гайка, т.е. происходит осевое движение гайки при неподвижном винте.
В передаче применяют метрическую, трапецеидальную и прямоугольную резьбы, с одним, двумя, тремя или четырьмя заходами.
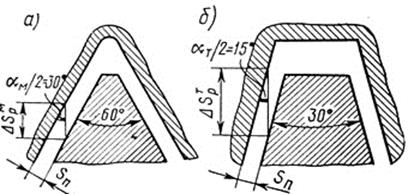 в)
в)
Рис.26.1
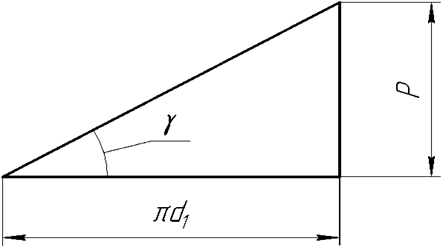
Здесь P – ход витка, т.е. расстояние между одноименными осевыми профилями одного витка по образующей делительного цилиндра: P = pz , где p - шаг – расстояние между соседними витками по образующей цилиндра.
При повороте винта на угол φ гайка поступательно перемещается на расстояние
l = φP/ (2 π ),
- функция перемещения передачи.
*В дифференциальной передаче винт 1 имеет две резьбы с разными шагами p1 и p2 одного направления (правого и левого).
ЛЕКЦИЯ № 11
Планетарные передачи.
Основные понятия. Конструкция.
Планетарными называются передачи, в которых “колеса–сателлиты” 2 обкатываются по центральному колесу 1 и опорному колесу О имеют подвижные оси, закрепленные на “водиле” Н. Планетарные передачи, используемые в виде редукторов, предназначены для преобразования угловой скорости при изменении моментов.
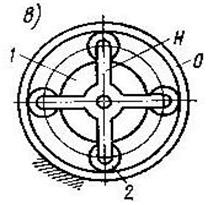
Входной вал – вал ведущего центрального (солнечного) колеса 1. Скорость 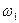 и момент Мкр передаются посредством сателлитов 2, обкатывающихся по неподвижному опорному зубчатому колесу О с внутренними зубьями. Выходной вал - вал водила Н, к которому через соединительную муфту присоединяется вал нагрузки.
и момент Мкр передаются посредством сателлитов 2, обкатывающихся по неподвижному опорному зубчатому колесу О с внутренними зубьями. Выходной вал - вал водила Н, к которому через соединительную муфту присоединяется вал нагрузки.
В конструкции может быть 2, 3, 4 сателлита. Таким образом, в передаче вращающих моментов одновременно задействовано несколько участков зубчатого венца солнечного колеса 1. Т.е. каждый сателлит передает уменьшенный вращающий момент. Это позволяет применять зубчатые колеса с меньшими модулями и значительно сократить габариты передачи.
11.2. Определение передаточного отношения передачи 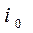 по плану скоростей.
по плану скоростей.
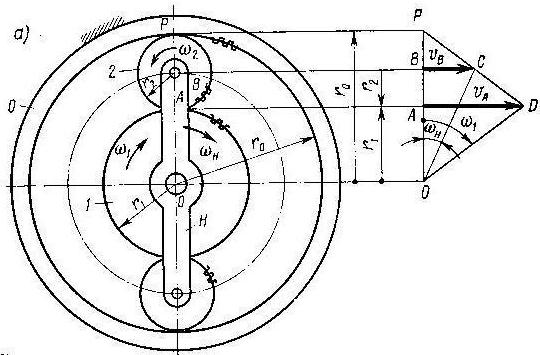
В соответствие с обозначениями рисунка 11.2:
Скорость точки контакта сателлита и опорного неподвижного колеса равна О, следовательно 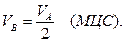
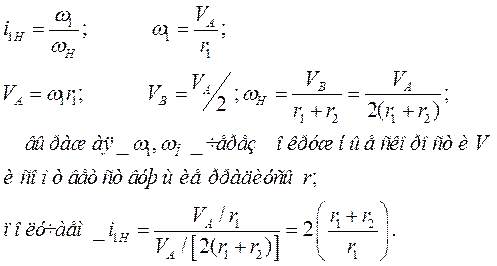
Окружная скорость центра колеса 2 равна скорости водила Н:
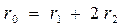
Следовательно:

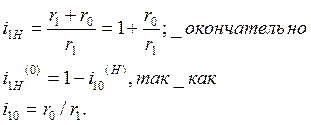
В этом случае 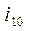 рассматривается как передаточное отношение от солнечного колеса к вращающемуся опорному колесу через паразитное колесо 2 при условно неподвижном “водиле”. Знак (-) учитывает, что опорное и центральное колеса вращаются в противоположных направлениях.
рассматривается как передаточное отношение от солнечного колеса к вращающемуся опорному колесу через паразитное колесо 2 при условно неподвижном “водиле”. Знак (-) учитывает, что опорное и центральное колеса вращаются в противоположных направлениях. 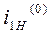 - неподвижное опорное колесо;
- неподвижное опорное колесо; 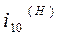 - неподвижное водило.
- неподвижное водило.
11.3. Определение i 0 передачи методом обращенного движения
Теорема Смирнова-Виллиса.
Рассмотрим планетарную передачу как обычную рядную. Для этого мысленно остановим водило и дадим возможность вращаться опорному колесу.
| Подвижный элемент | Угловые скорости | |
| При неподвижном колесе О | При неподвижном водиле Н | |
| 1. Ведущее колесо 1 | 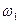
| 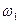 - - 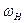
|
| 2. Опорное колесо 0 | 0 | - 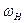
|
| 3. Водило | 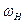
| 0 |
| 4. Сателлит 2 | 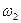
| 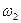 - - 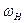
|
По данным таблицы записываем передаточное отношение и приходим к полученной ранее формуле.
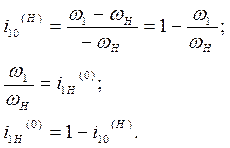

Для правильной работы планетарной передачи требуется выполнение условия соосности, которое используется как уравнение связи чисел зубьев колес в передаче.
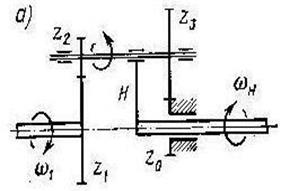
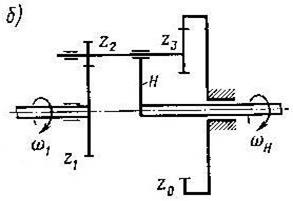
В соответствии с обозначениями рисунка 11.2 а):
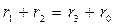 ;
;
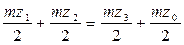 ;
;
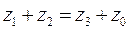 ;
; 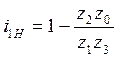 .
.
В соответствии с обозначениями рисунка 11.2 б):
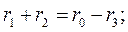
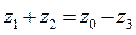 ;
;
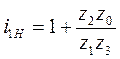 .
.
11.3. Распределение сил в планетарной передаче.
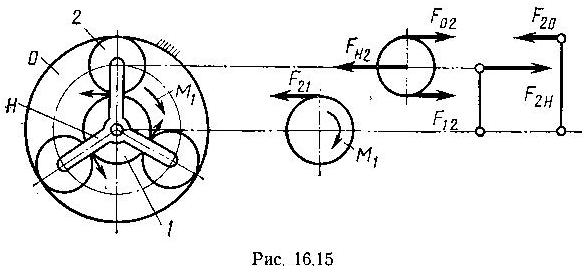
Считаем, что момент 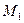 задан. Тогда окружная сила от солнечного колеса 1 на каждом сателлите 2 равна:
задан. Тогда окружная сила от солнечного колеса 1 на каждом сателлите 2 равна:
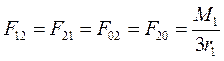 , где n = 3 – число сателлитов.
, где n = 3 – число сателлитов.
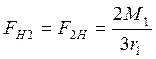 .
.
Расчет на прочность зубьев в планетарной передаче ведется по окружной силе, уменьшенной во столько раз, сколько сателлитов имеет передача.
11.4. Достоинства и недостатки планетарных передач.
Достоинства:
· компактность и малый вес.
· возможность получения больших 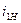 в одноступенчатой передаче до 36,
в одноступенчатой передаче до 36,
в двухступенчатой - до 1000.
· конструктивные преимущества (внутреннее зацепление обладает повышенной нагрузочной способностью вследствие небольших значений кривизны контактирующих профилей; уменьшение осевых усилий пропорционально количеству сателлитов).
Недостатки :
· большое количество деталей и необходимость повышенной точности их изготовления.
· сложность сборки.
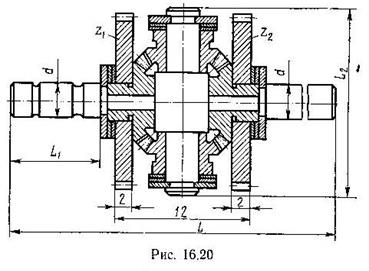
Дифференциальные механизмы.
Дифференциальный механизм можно получить из планетарного, если придать вращательное движение неподвижному колесу. Дифференциальный механизм приводится в движение двумя двигателями, имеет 2 входных вала и один выходной.
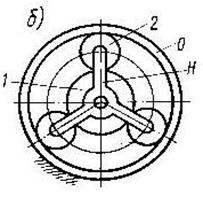
Подвижными становятся три основных звена (1, 3, Н). Рис.а) – с цилиндрическими зубчатыми колесами, рис.б) – с коническими зубчатыми колесами. На выходном валу можно получить либо сумму, либо разность угловых скоростей входных валов.
Применяются в приводах ведущих колес автомобиля, трактора (конические – с двумя степенями свободы) для обеспечения движения с разной скоростью по разным участкам дороги.
В соответствие с обозначениями рисунков 11.4 и 11.5:
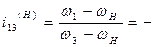
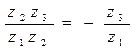 ;
;
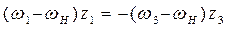 ;
;
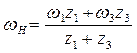 .
.
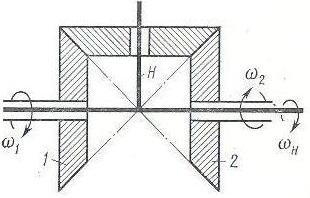
Рис.11.5
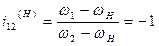 ;
;
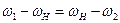 ;
;
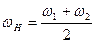 ;
;
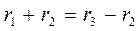 ;
;
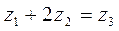 .
.
Можно использовать дифференциальные механизмы путем подачи одного двигателя (1 вход) на двух потребителей (2 выхода)
· при 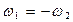 ;
; 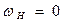 ;
;
· при 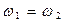 ;
; 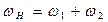 ;
;
· 
ЛЕКЦИЯ № 12
Волновые передачи.
12.1. Основные понятия. Конструкция.
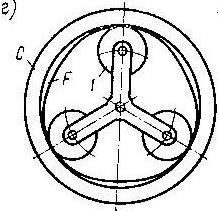
Волновые передачи являются разновидностью планетарных передач. В них передача движения осуществляется путем бегущей волновой деформации одного из колес. В волновой передаче одно из колес выполняется гибким. Для обеспечения зацепления со вторым жестким колесом гибкое колесо деформируется при помощи ролика, закрепленного на водиле Н. При вращении водила деформация гибкого колеса перемещается по окружности в виде бегущей волны, поэтому передача называется волновой, а водило генератором волн. Волновые передачи по конструктивному выполнению могут быть фрикционными и зубчатыми.
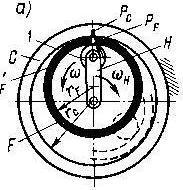
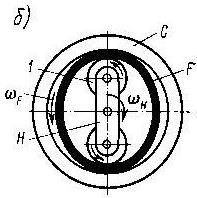
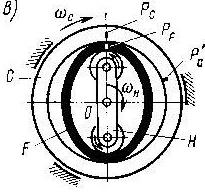
С - жесткое цилиндрическое неподвижное опорное кольцо (колесо),
F - гибкое колесо,
Н - водило.
Примем показанное положение перед началом вращения водила и отметим рисками Pc и PF соприкасающиеся точки на жестком опорном C и гибких кольцах F. Обозначим длину внутренней окружности жесткого кольца lC и гибкого кольца lF. При вращении водила, например в направлении по часовой стрелке, гибкое колесо вращается в обратном направлении, так как l F > lC . Считаем, что проскальзывание отсутствует. За один оборот водила гибкое кольцо повернется на один угол, определяемый дугой PCP / F , равной разности длин окружности lC – lF.
Чем меньше разница длин окружностей контакта жесткого и жесткого колец, тем меньше угол поворота гибкого кольца. Отсюда следует, что в этой передаче
происходит преобразование быстрого вращения водила, например с угловой скоростью в обратное направлению замедленного вращение гибкого кольца.
lC ,lF - длина внутренней окружности жесткого C и гибкого кольца F,
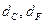 - диаметры внутренних окружностей С и F .
- диаметры внутренних окружностей С и F .
Отсюда, передаточное отношение:
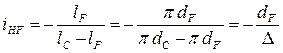 ,
, 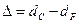 .
.
Если убрать водило, гибкое и жесткое колеса располагаются концентрично, при этом зазор равен 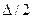 .
.
Фрикционные волновые передачи не нашли широкого применения, так как в процессе их работы происходит проскальзывание колес относительно друг друга.
Зубчатые волновые передачи
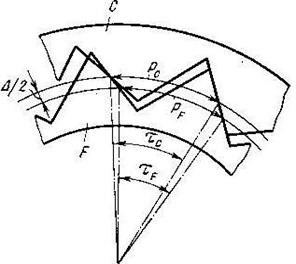
В передачах используются зубья остроконечные или эвольвентные.
При этом необходимо обеспечить следующие условия:
· окружные шаги p и модули m колес C и F должны быть одинаковы;
· делительный диаметр колеса F , dF должен быть меньше делительного диаметра колеса С, dC :
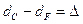 ;
; 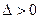 .
.
Рассмотрим схему с неподвижным опорным колесом С. При вращении волнообразователя H с угловой скоростью 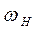 гибкое колесо F поворачивается c угловой скоростью
гибкое колесо F поворачивается c угловой скоростью 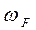 в направлении, противоположном
в направлении, противоположном 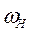 .
.
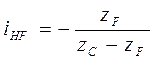 ;
; 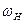 и
и 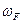 - разнонаправлены.
- разнонаправлены. 
За один оборот водила Н гибкое колесо F повернется в обратном направлении с 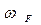 на угол
на угол 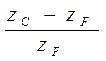 оборота.
оборота.
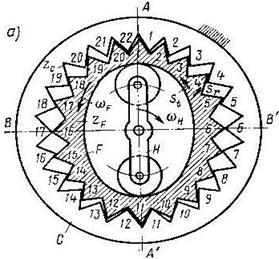
В схеме с неподвижным гибким колесом:
F – неподвижное(гибкое)
С – подвижное (жесткое)
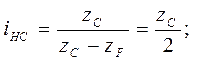 ωH и ωC - сонаправлены.
ωH и ωC - сонаправлены.
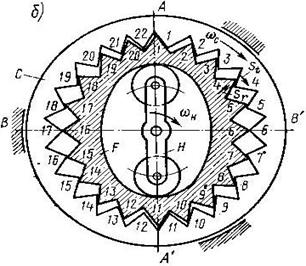
Для осуществления движения гибкого колеса относительно жесткого его зубья должны иметь возможность переходить из одной впадины в другую на зубчатом венце жесткого колеса. Такое разъединение зубьев показано для точек В и В/. Таким образом, за четверть оборота водила Н зубья гибкого колеса переходят из положения А в положение В, что соответствует повороту гибкого колеса F на половину шага. За полный оборот водила Н, колесо F повернется на 2 шага. В этом случае необходимо, чтобы разность чисел зубьев 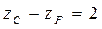 , то есть числу волн создаваемых генератором. Следовательно, тогда
, то есть числу волн создаваемых генератором. Следовательно, тогда 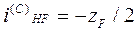 .
. 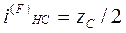 .
.
Число волн определяется конструкцией генератора. Для роликового генератора число волн в передаче определяется числом роликов. Различают двух, трех волновые и т.д. передачи. Угловые шаги 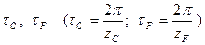 не равны, поэтому перед сборкой в гибкое колесо вставляется волнообразователь Н.
не равны, поэтому перед сборкой в гибкое колесо вставляется волнообразователь Н.
При вращении генератора волн непрерывное изменение гибкого кольца представляется как движение изгибной волны. Основным движением является радиальное Sr смещение зубьев гибкого колеса под действием роликов волнообразователя.
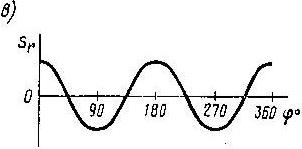
Так, например, зуб 4 под действием ролика волнообразователя, смещаясь в радиальном направлении Sr , давит на профиль одноименного зуба жесткого колеса, что приводит к смещению St либо гибкого колеса влево, если оно подвижно; либо к повороту St жесткого колеса вправо, если оно подвижно.
Учитывая, что 
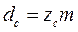 и
и 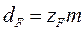
 передаточные отношения соответственно равны:
передаточные отношения соответственно равны:
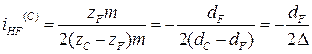 ;
;
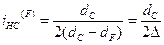 .
.
Передаточное отношение тем больше, чем меньше зазор 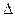 (чем мельче зубья и меньше модуль). В зубчатых волновых передачах с эвольвентным профилем используется стандартный исходный контур, угол зацепления
(чем мельче зубья и меньше модуль). В зубчатых волновых передачах с эвольвентным профилем используется стандартный исходный контур, угол зацепления 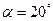 , высота зуба
, высота зуба 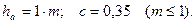
Для зубчатых волновых передач гибкое кольцо выполняют в виде тонкого стального стакана.
Достоинства волновой зубчатой передачи.
1. Возможность получать передаточное отношение порядка 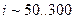 ; при этом
; при этом  ограничивается
ограничивается  зуборезного инструмента.
зуборезного инструмента.
2. Одновременное участие в зацеплении многих зубьев обеспечивает большую несущую способность.
3. Поломка одного зуба не приводит к выходу из строя передачи и не снижает точности движения.
4. Высокая кинематическая точность и плавность вращения.
5. Высокий КПД ( 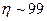 %, соответствует КПД зубчатого редуктора).
%, соответствует КПД зубчатого редуктора).
6. Возможность передачи движения в герметизированное пространство.
Назначение волновых зубчатых передач.
Механизмы систем дистанционного управления, механизмы настройки РЭА, приводы антенн, радиолокаторов, механизмы вертолетов, самолетов, ракет, станков.
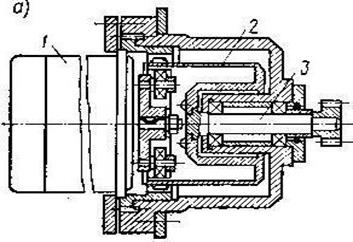
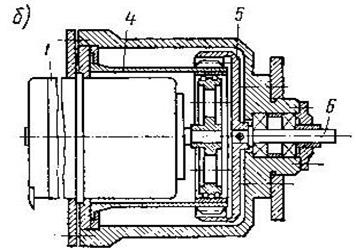
Лекция №13
Муфты
Муфты служат для соединения валов и осей, используются как предохранительные элементы конструкции, компенсаторы погрешностей сборки. По принципу действия бывают механические и электрические. Механические муфты разделяют на соединительные (глухие) и компенсирующие. Предохранительные механические – неуправляемые и самоуправляемые.
Соединительные муфты
Применяются для соединения соосных длинных валов, расположенных
в труднодоступных местах приборов, а также для соединения валов двигателей, потенциометров, тахометров с валами редуктора.
Глухие (втулочные и дисковые) муфты требуют строгой соосности соединяемых валов. Передаточное отношение соединительных муфт равно 1. При отклонениях i от 1 возникают кинематическая и люфтовая погрешности.
Виды погрешностей, возникающие при соединении валов.
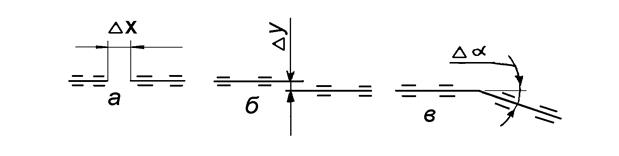
Δх- продольное осевое смещение;
Δу - поперечное осевое смещение;
Δα - смещение по углу.
Втулочная муфта
Втулочные муфты (глухие) применяют для жесткого соединения двух валов. В таких муфтах при отсутствии смещений по углу ∆α и поперечных смещений ∆y сложно скомпенсировать продольные осевые смещения ∆х.
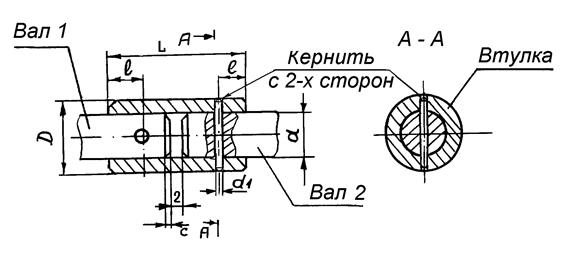
Конструкция этих муфт чаще всего бывает неразборной, динамические нагрузки не демпфируются, поэтому втулочные муфты применяют редко.
Расчеты таких муфт в приборных конструкциях сводятся к расчету штифтов на срез:
|
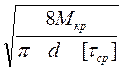 .
.
где d1 – диаметр штифта, мм;
Мкр – крутящий момент, передаваемый муфтой, Н·мм;
d – диаметр вала, мм;
[τср] - допускаемые напряжения среза штифта, Мпа.
Допускаемые напряжения среза штифта можно найти по выражению:
[τср]=(0.75…0,8)σв /n ,
где σв – временное сопротивление разрыву (предел прочности), МПа;
n – коэффициент запаса.
У материалов, рекомендуемых для изготовления штифтов втулочных муфт, σв имеет значения: Сталь 45 – 598 МПа, Сталь 50 – 628 МПа, Сталь 65Г – 736 МПа.
Предохранительные муфты
Лекция №
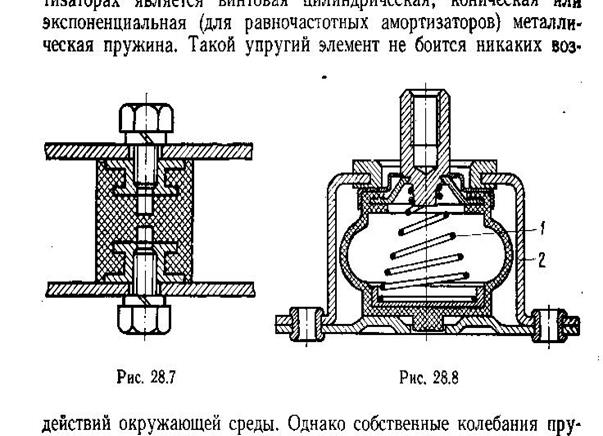
Упругие элементы
Основные определения
Упругие элементы (пружины) – детали, упругие деформации которых используются в работе различных механизмов и приборных устройств.
По геометрическим признакам упругие элементы делят на стержневые и оболочковые.
Стержневые делят на плоские, спиральные, винтовые.
Оболочковые делят на мембраны (мембранные коробки и их наборы), сильфоны и трубчатые пружины.
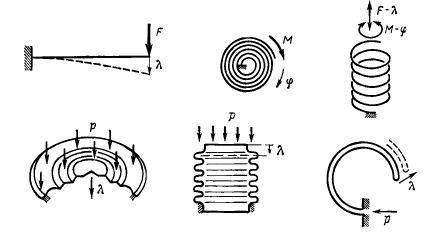
Простейшей конструкцией мембраны является круглая плоская, которую условно называют «хлопающей», такие мембраны используют в контактных группах.
Мембранные коробки разделяют на: манометрические, которые используют для измерения давления внутренних сред (масло, вода, газ), и анероидные, которые используют для измерения давления внешней среды; принцип действия такой коробки состоит в измерении разности давления внутри коробки, из которой откачен воздух и внешним давлением.
Сильфон – тонкостенная цилиндрическая трубка с поперечной кольцевой гофрировкой. Используют два конструктивных варианта: из цельнотянутой цилиндрической заготовки и собранные путем пайки (сварки) отдельных гофров.
По назначению упругие элементы делятся на следующие группы:
Измерительные пружины применяются в измерительных приборах, таких как манометры, динамометры, термометры и прочие. Основные требования - стабильность зависимости деформации от приложенного усилия и линейность рабочей характеристики.
Натяжные пружины обеспечивают силовой контакт между деталями. Основное требование - усилие прижатия должно быть постоянно.
Заводные пружины (пружинные двигатели) используются в часах и лентопротяжных механизмах. Основное требование - способность запасать необходимую энергию упругих деформаций.
Пружины кинематический устройств – пружины упругих опор. Основное требование – гибкость и прочность.
Пружины амортизаторов должны выдерживать переменные нагрузки, удары и большие перемещения.
Пружины фрикционных и храповых муфт - винтовые пружины кручения, которые с натягом надевают на валы, что позволяет сцеплять валы с надетой на них втулкой. Основное требование – высокая износостойкость.
Токоведущие упругие элементы - тонкие винтовые или спиральные пружины, которые одновременно совмещают и функцию измерителя. Основное требование – малое электрическое сопротивление.
Разделители сред обеспечивают возможность передачи усилия или перемещение от одной среды к другой посредством одинарных мембран или сильфонов.
Материалы упругих элементов
Материалы упругих элементов должны обладать следующими свойствами:
- высокой упругостью;
- высокой пластичностью;
- прочностью и выносливостью;
а также в особых условиях эксплуатации - электропроводимостью, немагнитностью, коррозионной стойкостью и термостойкостью.
К таким материалам относятся:
- нержавеющие и легированные стали У8A, У10A, 65Г;
- бронзы БркМцЗ-1, Бр ОЦ 4-3;
- латуни Л62, Л80;
- кварц, фторопласты, резина.
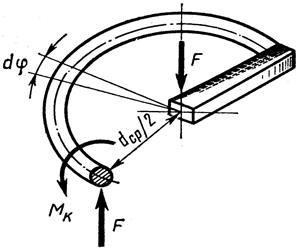
Цилиндрические пружины
Цилиндрическая пружина сжатия или растяжения круглого сечения

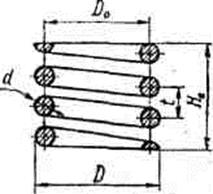
Параметры:
d – диаметр проволоки,
D 0– средний диаметр пружины,
D – наружный диаметр,
t – шаг навивки.
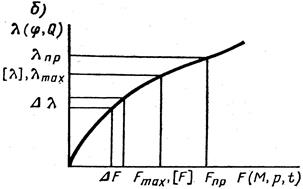
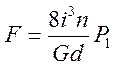 , где
, где 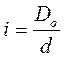 индекс пружины
индекс пружины
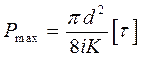 , где
, где 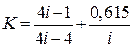
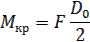
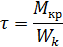
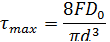
Конические пружины сжатия
Коническая пружина ( t = const): круглого сечения
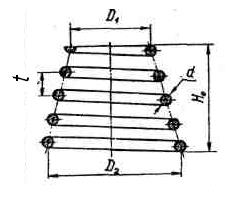
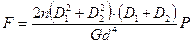
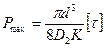 где
где 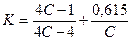 ;
; 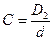
Конические пружины можно сжимать до высоты, равной толщине витка. При Hо/ D ≤ 4 их можно применять без направляющих, тогда как цилиндрические пружины при H 0 / D ≥ 4, во избежание выпучивания, должны иметь направляющие в виде стержня или стакана.
Устойчивость пружин сжатия
При проектировании пружин сжатия для обеспечения необходимой продольной устойчивости выбирают H / D 0 < 3, при H / D 0 > 3 необходимо использовать пружины в сочетании с внутренними или внешними направляющими. Для уменьшения габаритов пружин в сжатом состоянии и увеличении устойчивости используют конические пружины. Высота конической пружины в сжатом состоянии равна диаметру проволоки. Особенностью конической пружины является сугубая нелинейность характеристики из-за разной величины диаметров витков.
Классы винтовых цилиндрических пружин сжатия и растяжения из стали круглого сечения
| Класс | Тип пружины | Нагружение | Выносливость N циклов, нс менее | Инерционное соударение витков |
| I | Сжатия Растяжения | Циклическое | 5×106 | Отсутствует |
| II | Сжатия Растяжения | Циклическое и статистическое | 1×105 | Отсутствует |
| III | Сжатия | Циклическое | 2×103 | Наблюдается |
Расчет и выбор винтовых цилиндрических пружин сжатия и растяжения из стали круглого сечения с индексом С = 4...12 должны производиться по ГОСТ 13764—68... 13776—68.
Согласно ГОСТ 13764—68 имеется три класса пружин в зависимости от выносливости (табл. ). При этом отсутствие соударения витков у пружин сжатия определяется условием V0/Vкр≤1, где Vкp—критическая скорость пружины сжатия, м/с (соответствует возникновению соударения витков пружины от сил инерции). Все статические пружины, длительно пребывающие в деформированном состоянии и периодически нагружаемые со скоростью V0 < Vкp, относятся к I классу.
Упругие несовершенства
Это упругое последействие (при нагрузке и разгрузке деформация происходит не мгновенно, а с запаздыванием); релаксация (при отсутствии нагрузки продолжаются изменения внутреннего сопротивления материала); (несовпадение характеристик при нагрузке и разгрузке) – упругий гистерезис, %.
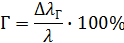
Гистерезис сильнее проявляется в пружинах сложной конфигурации: Г ~0,1…1%
С увеличением нагрузки гистерезис проявляется более заметно (т.к. возрастают напряжения в материале).
При расчете сложных пружин коэффициент запаса n = 5…10.
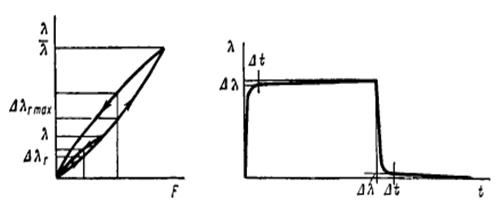
Плоские пружины
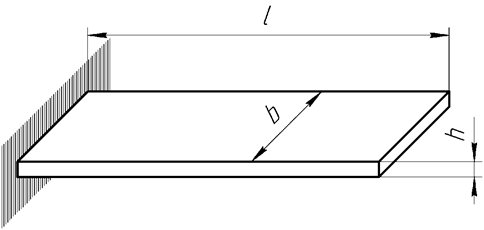
Наибольшее распространение имеют плоские пружины в форме консольной балки. Их применяют в контактных группах, скользящих токоподводах, контактах потенциометров, а также в виде упругих опор, в качестве элементов измерительного устройства, и в других случаях, когда плоская форма пружины хорошо вписывается в габарит механизма. Чаще плоские пружины изготавливают из листового материала с b >> h . Пружина должна обладать достаточной прочностью и обеспечивать заданное перемещение свободного конца.
Форма сечения чаще всего прямоугольная или круглая.
Эта группа пружин очень разнообразна как по конструкции, так и по назначению. По конструктивному оформлению различают прямые, изогнутые и спиральные пружины. Материал плоских пружин работает на изгиб.
Прямые плоские пружины с прямоугольным сечением применяют при малых линейных перемещениях и относительно небольших усилиях; например, в качестве контактных пружин реле и переключателей, в фиксаторах и тормозах, как упругие опоры и направляющие.
Прямая пружина требует много места, так как по сравнению с возможной деформацией она имеет большую длину; материал прямой пружины (ленточная сталь, бронза и т. п.) может быть применен в естественном состоянии. При этом пружину по длинной стороне следует располагать по длине проката или под небольшим углом к нему.
Способ крепления и приложения нагрузки
Уравнение упругой характеристики 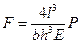
Максимальная нагрузка Рmax 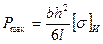
Вид пружины
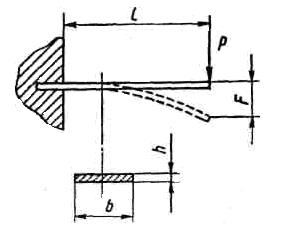
Вид пружины
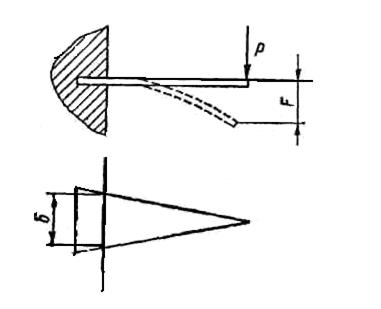
Уравнение упругой характеристики 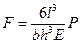
Максимальная нагрузка Рmax 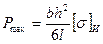
22.1. Формулы для определения геометрических параметров
Максимальное напряжение в сечении пружины:
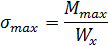
Моменты сопротивления для прямоугольного и круглого сечений:
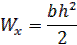
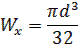
Перемещение свободного конца:
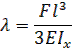
Из этих соотношений получаем ширину b,толщину h и жесткость k плоской пружины:
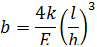
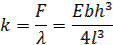
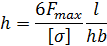
Для обеспечения правильной функциональности плоской пружины соотношение величин надо выбирать следующее:
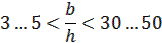
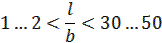
При b / h < 3…5 пружина чувствительна к поперечным нагрузкам;
При b / h > 30…50 пружина чувствительна к смещению линии приложения нагрузки;
При l / b < 1…2 (пружина короткая и широкая) оказывают влияние местные деформации в закреплении;
при l / b > 30…50 - слишком большой габарит.
Процесс проектирования плоской пружины – перебор сочетания размеров l / b
и b / h из условий прочности и жесткости. При этом задается ряд значений l / h
и путем перебора этих значений определяются другие параметры.
Характеристики ТБ пружин
1) Чувствительность S
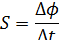
| 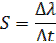
| 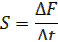
|
где Δt – диапазон изменения [о С].
Для получения лучшей чувствительности ( S ) пассивной слой изготавливают из сплава инвар (α ≈ 0); активный слой - из латуни, хромо-никелевых сталей
(α-намного выше).
2) Жесткость K
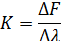
ТБ пружины имеют жесткость выше, чем плоские, поэтому меньше сказывается влияние сил сопротивления (трения);
3) Температурный коэффициент электрического сопротивления материала ρ [Ом∙м];
4) Допустимая температура нагрева τ [°С];
5) Удельный изгиб А [1/°C]
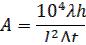
Удельный изгиб рассчитывается по результатам измерения перемещения конца λ, закрепленной консольно пружины длиной l , толщиной b при нагреве Δt .
Маркировка пружин
Обозначение включает 3 параметра: A , ρ , t
Например: ТБ-1254
A – точное значение величины
В примере: A=12 [1/°C]
ρ и t – баллы (5-балльная шкала)
В примере: ρ = 0,09 ~ 0,14 Ом∙м; t = 140 °C
Виды соединения пружин
Последовательное соединение
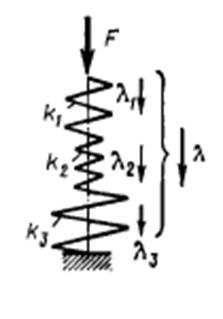
| 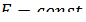 , ,
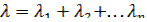
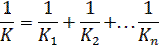
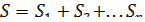
|
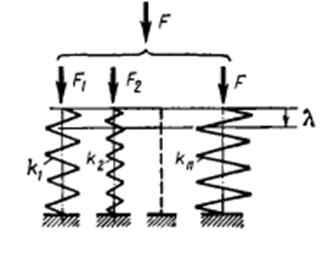
Параллельное соединение
| 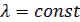
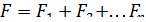
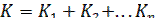
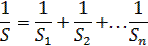
|
Смешанное соединение
Это соединение нескольких упругих элементов; при их расчете сначала определяются S или K блоков с параллельным соединением, а затем эти блоки рассматриваются как элементы, соединенные последовательно.
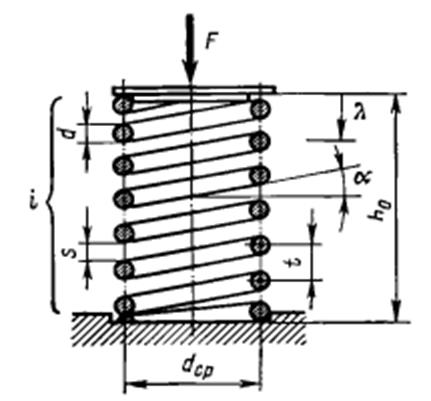
h 0 – начальная длина (высота) пружины
λ - рабочий ход
i – число витков
H0 – высота пружины при max F сжат. (раст.)
C = D 0 / d – индекс пружины
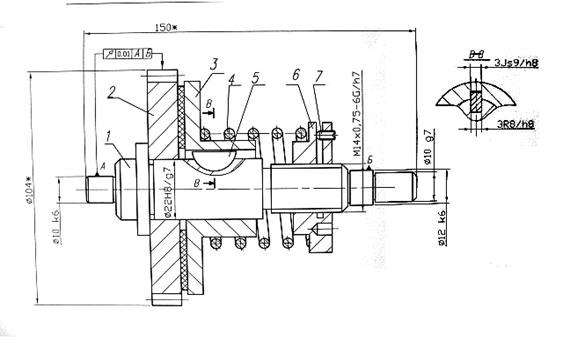
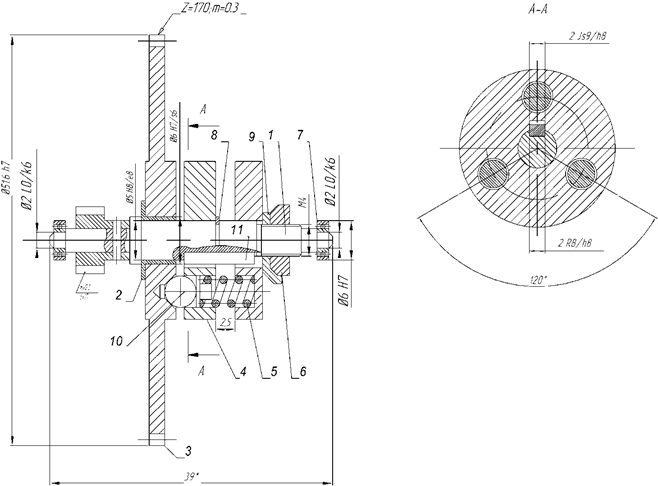
Приложение. Винтовые передачи
Передачи с трением скольжения
В винтовых передачах с трением скольжения применяются трапецеидальная, упорная, метрическая, окулярная, прямоугольная резьба.
Резьба трапецеидальная (профиль по ГОСТ 9484—81). Стандартизована в пределах диаметров 8...630 мм и шагов 1,5...40 мм, с допусками по ГОСТ 9562—81 (однозаходная, ГОСТ 24738—81) и в пределах диаметров 10...320 мм, шагов 1,5...40 мм, числа заходов 2...8 (многозаходная, ГОСТ 24739—81). Диаметры, шаги и поля допусков резьб применительно к винтовым передачам приборостроения даны в табл. №
Таблица № Поля допусков трапецеидальных резьб для винтовых передач
| Наружная резьба | Внутренняя резьба | ||||
| Размер | Степень точности | Основное отклонение | Размер | Степень точности | Основное отклонение |
| d d2 d3 | 4...6; Т* 6...9; 7*…10* 6...9; 7*...10* | h с; е; g; h h | D4 D2 D1 | Т; Т* 6...9; 7*...9* 4; 4* | Н Н Н |
Примечания: 1. Приведены поля допусков ограничительного отбора.
2. Т — допуски по особым нормам. *Для многозаходной резьбы.
Таблица Длины свинчивания трапецеидальной резьбы, мм
| P | N | L | P* | N* | L* | P** | N** | L** |
| 1,5 | 5...15 | Свыше 15 | 2 | 8...24 | Свыше 24 | 2 | 8...25 | Свыше 25 |
| 2 | 6...19 | » 19 | 3 | 14...32 | » 32 | 3 | 12...36 | » 36 |
| 3 | 10...28 | » 28 | 4 | 15...43 | » 43 | 5 | 21...63 | » 63 |
| — | — | — | 5 | 18...53 | » 53 | 6 | 25...75 | » 75 |
| — | — | — | 8 | 30..85 | » 85 | 8 | 24..100 | » 100 |
| — | — | — | — | — | — | 10 | 42..125 | » 125 |
Примечание. N — нормальная длина свинчивания, L -большая.
Диаметр резьбы свыше 11,2 мм до 22,4 мм. ** Диаметр резьбы свыше 22,4 мм до 45 мм.
Таблица № Применяемость полей допусков трапецеидальных резьб
в зависимости от длин свинчивания
| Диаметр резьбы | Длина свинчивания | Класс точности | ||
| точный | средний | грубый | ||
| d2 | N | 6е; 6g; 7*е; 7*g S | 7е; 7g; 8с*;8е* 8е* | 8с;8е: 9с 9с* |
| L | 7е; 8е* | 8е; 8с* | 9с; 10с* | |
| d2 | N | 6H; 7Н* | 7Н; 8Н* | 8H: 9H* |
| L | 7Н; 8Н* | 8H; 9H * | 9H; 9H* | |
Примечание. 8е, 8H — поля предпочтительные.*Для многозаходной резьбы.
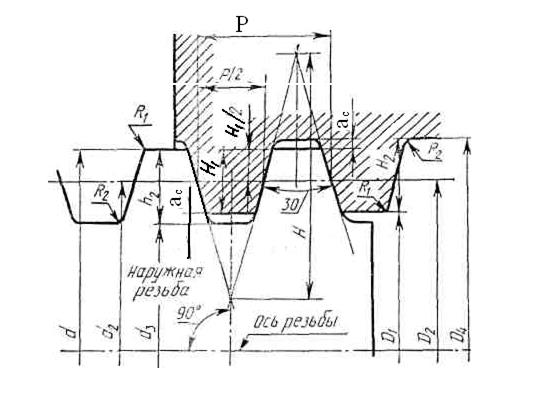
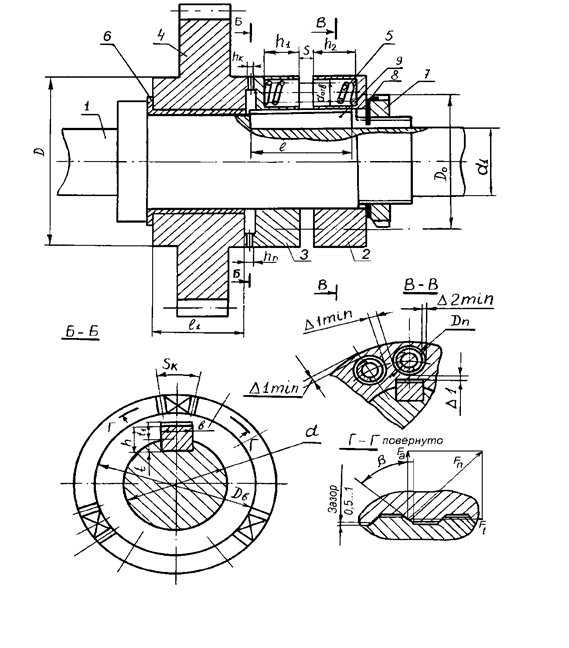
Рис. № Резьба трапецеидальная
Таб. № Размеры резьбы трапецеидальной, мм
| d | Р | Число заходов | d | Р | Число заходов | d | Р | Число заходов |
| 8 | 1,5 | 1 | 16 | 4 | 1...6 | 28* | 3 | 1...8 |
| 9 | 1,5; 2 | 1 | 18 | 2; 4 | 28* | 5 | 1; 2; 4; 8 | |
| 10 | 1,5; 2 | 1...8 | 20 | 2; 4 | 1...8 | 28* | 8 | 1...4 |
| 11 | 2; 3 | 1 | 22 | 3: 5; 8 | 30 | 3; 6; 10 | ||
| 12 | 2 | 1...8 | 24 | 3 | 1...8 | 32 | 3; 6 | 1...8 |
| 12 | 3 | 1...6 | 24 | 5 | 1.2.4 | 32 | 10 | 1: 2: 4 |
| 14 | 2; 3 | 1 | 24 | 8 | 1...4 | 34 | 3; 6; 10 | |
| 16 | 2 | 1...8 | 26 | 3; 5; 8 |
Примечания: 1. Число заходов резьбы по ряду: 1, 2, 3, 4, 6, 8.
2. Н = 1,866Р; Н1 = 0,5P; H2 = h2 = 0,5P + ac.
3. D2 = d2 = d - 0,5P, d3 = d - 2 H2 Н1 = -D2 + Н1, D1 = D4-2 Hz.
4. R1max = 0.5ас R2max = ас
6. Радиальный азор ас при шаге Р до 1,5 мм — 0,15 мм, при Р свыше 1,5 мм до 5 мм — 0,25 мм, при Р свыше 5 мм до 12 мм — 0,5 мм. .
* Предпочтительны только для однозаходной резьбы.
ЛЕКЦИЯ №15
Успокоители
Успокоители (демпферы) служат для устранения вредных собственных колебаний подвижной системы прибора. Почти в каждом приборе (рис. ) имеется подвижная система 1, которая под влиянием различных причин может быть выведена из равновесия и войти в колебания относительно неподвижной части, например, корпуса 2. Колебания могут быть вызваны ударами, вибрациями, ускорениями; даже при резком изменении измеряемой величины могут возникнуть собственные колебания подвижной системы прибора. Эти колебания приводят к искажению показаний приборов, затрудняют пользования ими, могут вообще вывести прибор из строя.
Успокоитель создает в движущейся системе прибора сопротивление, на преодоление которого расходуется энергия колебаний системы. Благодаря этому колебания затухают – успокаиваются.
Случай 1
Допустим, что в ПУ не установлен успокоитель, тогда уравнение примет вид:
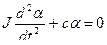 или
или 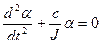
Решение уравнения имеет вид:
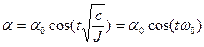 , ,
| (2) |
где α0 – угол отклонения системы от начального положения равновесия
при t = 0 и 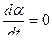 ;
; 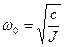 – круговая частота собственных колебаний.
– круговая частота собственных колебаний.
Из выражения (2) видно, что если систему вывести из состояния равновесия на угол α0, то она будет совершать незатухающие колебания по косинусному закону. График приведен на рисунке 3.
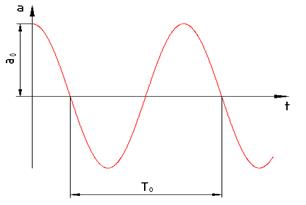
рис. 3
Период собственных незатухающих колебаний равен:
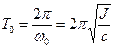
Очевидно, что чем больше момент инерции J и меньше жесткость упругого элемента c, тем больше Т0.
Частота собственных незатухающих колебаний будет в этом случае равна:
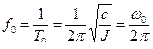
Наибольшее отклонение системы за период Т0 - амплитуда колебаний равная 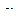 .
.
Случай 2
Рассмотрим случай, когда успокоитель в ПУ установлен. Тогда уравнение (1) будет иметь вид
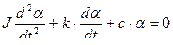
| (3) |
Характер движения подвижной системы прибора полностью определяется степенью успокоения (демпфирования) 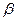 и круговой частотой собственных колебаний
и круговой частотой собственных колебаний 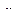 . Величина
. Величина 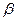 определяется по формуле:
определяется по формуле:
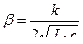 – степень успокоения (демпфирования)
– степень успокоения (демпфирования)
Если умножить 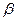 на
на 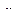 :
:
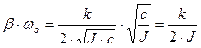 ,
,
то коэффициент успокоения k можно записать как:
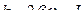 .
.
Тогда, в приведенном виде исходное уравнение (3) имеет вид:
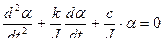
или
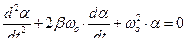
Рассмотрим влияние 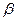 и
и 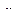 на характер движения подвижной системы рассмотрев три варианта:
на характер движения подвижной системы рассмотрев три варианта:  ;
;  ;
;  .
.
1. При  решение имеет вид:
решение имеет вид:
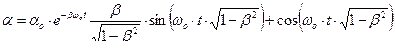
| (4) |
Из решения (4) видно, что с течением времени амплитуда колебаний будет убывать, т.е. колебания будут затухающими (рис. 4).
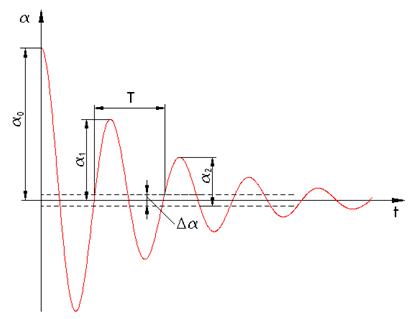
рис. 4
Установившейся считают подвижную систему, если колебания относительно положения равновесия не превосходят малой наперед заданной величины  , измеряемой в радианах. Для упрощения введен коэффициент
, измеряемой в радианах. Для упрощения введен коэффициент 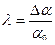 , характеризующий относительную точность установки системы в положение равновесия.
, характеризующий относительную точность установки системы в положение равновесия.
Время в течение, которого подвижная система приходит в положение равновесия, называют временем успокоения 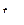 .
.
Из сравнения выражений (2) и (4) следует, что введение в систему успокоителя изменило частоту колебаний системы:
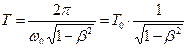
Таким образом, при 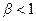 период
период 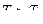 и по мере приближения
и по мере приближения 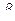 к единице, период
к единице, период  приближается к бесконечности, а колебания системы к апериодическому движению.
приближается к бесконечности, а колебания системы к апериодическому движению.
Для определения быстроты затухания колебаний вводится дополнительно характеристика - декремент затухания  , которым называют отношение предыдущей амплитуды
, которым называют отношение предыдущей амплитуды  колебания к последующей
колебания к последующей  , т.е.
, т.е.
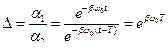 .
.
Наряду с декрементом затухания  в расчетах используют логарифмический декремент затухания
в расчетах используют логарифмический декремент затухания 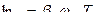 .
.
2. При 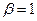 решение примет вид:
решение примет вид:
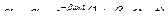
| (5) |
Режим колебаний при 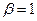 называется критическим режимом. В этом режиме в системе нет колебаний, и она долго подходит к положению равновесия (кривая 1 на рис. 5).
называется критическим режимом. В этом режиме в системе нет колебаний, и она долго подходит к положению равновесия (кривая 1 на рис. 5).
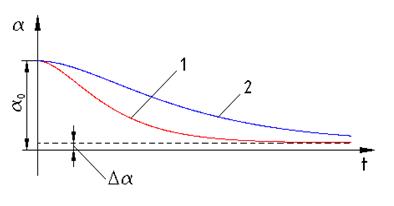
рис. 5
3. Решение при 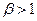 .
.
В этом случае также нет колебаний в системе, но система будет еще медленнее приближаться к положению равновесия (кривая 2 на рис. 5). В целом движение системы при 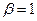 и
и 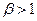 к положению равновесия называется апериодическим. Вывод: чем больше
к положению равновесия называется апериодическим. Вывод: чем больше 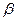 , тем медленнее система движется к состоянию покоя.
, тем медленнее система движется к состоянию покоя.
Вернемся к случаю, когда 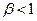 - это наиболее часто встречающийся на практике случай.
- это наиболее часто встречающийся на практике случай.
Подставив значение Т в выражение для  , получаем:
, получаем:
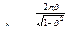
Из этого выражения видно, что, задаваясь величиной степени успокоения 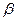 , можно определить декремент затухания
, можно определить декремент затухания  , а случае когда в приборе необходимо обеспечить определенный декремент затухания
, а случае когда в приборе необходимо обеспечить определенный декремент затухания  , то необходимая величина степени успокоения
, то необходимая величина степени успокоения 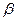 может быть подсчитана по формуле:
может быть подсчитана по формуле:
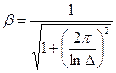
При расчете времени успокоения 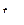 чаще всего пользуются коэффициентом
чаще всего пользуются коэффициентом 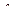 .
.
Время успокоения 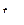 подсчитывается по формуле:
подсчитывается по формуле:
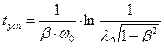
или
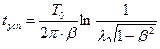
Итак, для расчета успокоителя должны быть заданы 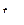 , J , c,
, J , c, 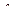 .
.
Расчет успокоителей.
Так как введенное в систему успокоение не только гасит собственные
колебания системы, но и влияет на ее частотные характеристики, то расчет успокоителя зависит от назначения и условий работы прибора. Это значит, что сначала в зависимости от предъявляемых требований надо определить необходимую степень успокоения для данного прибора, затем выбрать тип успокоителя и произвести расчет его основных параметров. В техническом задании на расчет прибора (или успокоителя) может быть указано, что успокоитель должен обеспечить необходимое затухание собственные колебаний системы в заданное время, обеспечить заданный коэффициент затухания колебаний (декремент затуханий), заданную амплитудную или фазовую погрешность прибора при исследовании колебательного процесса.
Определение необходимой степени успокоения.
Допустим, что по техническим условиям требуется обеспечить такое затухание собственных колебаний подвижной системы прибора, при котором начальное отклонение системы x0 должно уменьшиться до минимального xmin в течение заданного времени успокоения tусп (рис. ).
Так как практическое значение имеют только максимальные отклонения подвижной системы прибора, то для упрощения расчетов применяется уравнение экспоненты, огибающей вершины кривой колебаний:
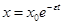 .
.
Тогда в соответствии с техническими условиями
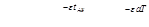
Или, введя степень успокоения  ,
,
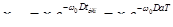 .
.
Из этого уравнения находим искомую степень успокоения:
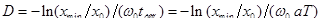 .
.
Производя преобразования, получаем:
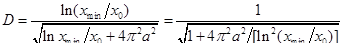 .
.
Необходимо отметить, что при сравнительно больших степенях успокоения
(D > 0 ,7) подвижная система прибора делает не более одного полуколебания.
Выбор типа успокоителя.
Наиболее распространенными являются успокоители, позволяющие получать в подвижной системе прибора линейное сопротивление. К таким успокоителям могут быть отнесены воздушные, жидкостные, и магнитоиндукционные успокоители. Воздушные и жидкостные успокоители в большинстве случаев выполняют поршневыми. Преимуществом жидкостных успокоителей является возможность получения практически любой степени успокоения в подвижной системе прибора. Но при этом, во-первых, приходится принимать меры предохранения от вытекания из них жидкости во внутренние полости прибора; во-вторых, вследствие зависимости вязкости жидкости от изменения температуры сопротивление, создаваемое успокоителем, также изменяется. Одинаково хорошо работают в широком диапазоне температур, мало изменяя вязкость, жидкости, полученные на основе кремнийорганических соединений.
Работа воздушного успокоителя почти не зависит от температуры окружающей среды. Но свойство сжимаемости воздуха может нарушить режим работы. И как следствие, воздушные приборы неэффективны в приборах, применяемых в условиях разреженного пространства. Расчеты успокоителей носят приближенный характер. В связи с этим в воздушных и жидкостных успокоителях предусматривают возможность регулирования проходных сечений рабочих отверстий, например, посредством регулировочных винтов.
Классификация успокоителей.












Рис. 7.
Все перечисленные группы успокоителей состоят из отдельных видов, характеризующихся в основном конструктивными признаками.
Воздушные успокоители
В электроизмерительных и других приборах, в которых требуется небольшая величина коэффициента успокоения k, применяются воздушные успокоители двух типов: крыльчатые и поршневые.
Воздушный крыльчатый успокоитель приведен на рис. 8.
Он состоит из закрытой неподвижной камеры прямоугольного сечения (1) и крыла (2), жестко соединенного с подвижной системой прибора. При движении системы по обеим сторонам крыла создается разное давление и возникает сила сопротивления движению, пропорциональная скорости. Для увеличения силы сопротивления применяют успокоитель с двумя крыльями, расположенными симметрично относительно оси подвижной системы. Чтобы исключить задевание крыла о стенки камеры делают зазор 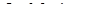 .
.
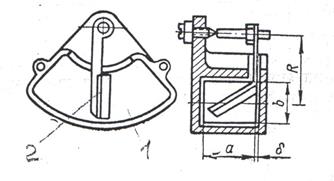
рис. 8
Уравнение движения системы с этим успокоителем имеет вид:
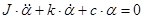 ,
,
следовательно,  .
.
Воздушный поршневой успокоитель приведен на рис. 9.
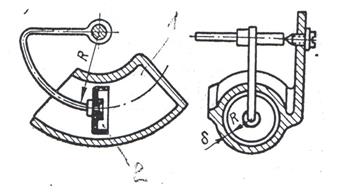
рис. 9
Он состоит из камеры 1 и перемещающегося в ней поршня 2, который жестко соединен с подвижной системой прибора. Между поршнем и стенками цилиндра делают зазор 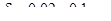 .
.
Поршневые успокоители прочнее крыльчатых и при равных площадях сечения камер имеют коэффициент успокоения k на 25-30% больше, чем крыльчатые.
Предыдущее уравнение движения справедливо и для поршневого успокоителя, но здесь 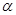 - угол отклонения поршня.
- угол отклонения поршня.
В воздушных успокоителях коэффициент k почти не зависит от изменения температуры, так как при этом коэффициент вязкости воздуха почти не изменяется.
Следует отметить, что при большой амплитуде и сравнительно низкой частоте колебаний системы обычно получается вполне достаточное успокоение
Жидкостные успокоители
Эти успокоители имеют сравнительно большой коэффициент успокоения k, поэтому они применяются в самопишущих приборах и других приборах с большими массами 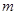 и моментами инерции J подвижных систем.
и моментами инерции J подвижных систем.
Резервуарные успокоители
Наиболее простые. Они представляют собой резервуар (обычно корпус прибора), заполненный жидкостью. В этой жидкости находится вся внутренняя часть прибора, в том числе его чувствительные элементы. Например, в сейсмографе СП-48 (используется при разведке полезных ископаемых) в жидкости находятся магниты и жестко закрепленные индукционные катушки. При движении магнитов в катушках возникают ЭДС. Для создания успокоения подвижной системы корпус прибора заполнен трансформаторным маслом.
Необходимая степень успокоения получается за счет изменения вязкости рабочей жидкости.
Жидкостной поршневой успокоитель.
Цилиндр 2, рис. 12, заполнен жидкостью. В нем перемещается поршень 1, соединенный с подвижной системой прибора.
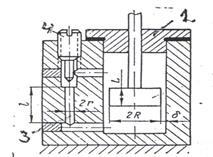
рис. 12
При движении поршня создается разность давлений по его обеим сторонам и жидкость перетекает из одной полости цилиндра в другую через зазор между стенками цилиндра и поршнем и капилляр 3. Винтом 4 можно изменять проходное сечение капилляра и регулировать величину коэффициента успокоения k.
Жидкостный пластинчатый успокоитель.
Успокоитель, рис. 13, состоит из резервуара, наполненного жидкостью, и ряда параллельно расположенных тонких пластин, жестко соединенных с подвижной системой прибора, и движущихся между пластинами, соединенными жестко с основанием прибора.
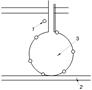
рис. 1
На рис. 13а показан элемент конструкции успокоителя, а на рис. 13б – схема успокоителя.
Жидкостный капиллярный (капельный) успокоитель.
Применяется для успокоения поперечных колебаний подвижной системы прибора на растяжках, два отверстия, через которые проходят растяжки 1 рис. 14, заполняются каплями масла.
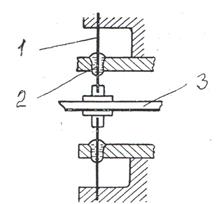
рис. 14
Масло не тормозит вращение растяжек, но успокаивает их поперечные колебания. Жидкость в рабочем капилляре удерживается за счет капиллярных сил. Используются эти успокоители в вибраторах.
Недостатком жидкостных успокоителей является изменение коэффициента успокоения, вследствие изменения вязкости жидкости при изменении температуры.
В успокоителях применяются трансформаторные и турбинные масла и их смеси, а также специальные жидкости.
Для расчета успокоителя должны быть заданы 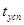 , J , c,
, J , c, 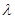 .
.
Чтобы выбрать тип успокоителя и определить его конструктивные параметры, необходимо определить величину требуемого коэффициента успокоения k.
Контрольные вопросы.
1. В каких приборах для устранения вредных собственных колебаний подвижной системы прибора используют успокоители?
2. Какими условиями эксплуатации могут быть вызваны колебания в подвижной системе прибора?
3. Что приводит к искажению показаний приборов, затрудняют пользования ими и пр. в случае отсутствия успокоителя?
3.Что такое степень упокоения?
Амортизаторы
Амортизаторы применяют для защиты приборов от внешних воздействий. Внешние воздействия на прибор могут быть переданы от работающего рядом оборудования, имеющего несбалансированные подвижные части, или в результате использования прибора в сложных динамических условиях, когда непосредственно на него передаются внешние нестационарные нагрузки. Защиту приборов от внешних воздействий разделяют на два вида: активная амортизация, когда источник возмущающих воздействий (оборудование) изолируется от опорного основания, и пассивная амортизация, когда сам прибор изолируют от основания, к которому приложены динамические нагрузки. Амортизацию называют противоударной, если она обеспечивает защиту приборов от ударных воздействий, и виброизолирующей, если осуществляется защита от механических колебаний. При разработке и эксплуатации приборов чаще всего приходится иметь дело с пассивной амортизацией.
В случае пассивной амортизации для уменьшения действия вибрационных и ударных нагрузок, вызывающих ускоренный износ деталей прибора, их деформацию, появление погрешностей в показаниях, применяют упругие подвесы – амортизаторы, на которых подвешивают отдельный прибор (или приборную доску), в частности, на летательном аппарате.
Эффект от введения амортизации характеризуют отношением амплитуды колебания амортизированного прибора к амплитуде колебания неамортизированных частей, на которых укрепляют прибор (или приборную доску). Это отношение, называемое коэффициентом амортизации, при правильно подобранном амортизаторе всегда меньше единицы. Цель амортизации – уменьшить этот коэффициент до возможно меньшего значения.
Наиболее часто в качестве упругих элементов используются винтовые или конические пружины или резиновые (прорезиненные) элементы.
Следует отметить, что в большинстве случаев амортизаторы используются в сочетании с успокоителями.
Рис.
Следовательно, график на рис.3 может характеризовать и изменение коэффициента передачи силы в зависимости от отношения угловых частот qa.
Из графика видно, что точке 1 соответствует коэффициент передачи силы, равный единице, передаваемая сила равна возмущающей. Это значит, что прибор жестко прикреплен к основанию без амортизации. График также показывает, что если отношение частот qa < 1,41 (точка В), то амортизатор увеличивает передаваемую силу. Анализ графика показывает, что коэффициент жесткости должен быть такой, чтобы угловая частота ω a собственных колебаний прибора на амортизаторе была мала по сравнению с угловой частотой ω возмущающей силы.
Коэффициент амортизации.
При наличии успокоителя (ka 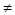 0) коэффициент динамичности не прямо пропорционален введенному в рассмотрение коэффициенту передачи силы. Теперь на прибор действует не только сила упругости с a xa амортизатора, но и сила успокоения, пропорциональная скорости относительного движения. Амплитуда этой силы
0) коэффициент динамичности не прямо пропорционален введенному в рассмотрение коэффициенту передачи силы. Теперь на прибор действует не только сила упругости с a xa амортизатора, но и сила успокоения, пропорциональная скорости относительного движения. Амплитуда этой силы  . Сила упругости амортизатора изменяется по закону синуса, сила успокоения - по закону косинуса, т.е. их векторы смещены на 90
. Сила упругости амортизатора изменяется по закону синуса, сила успокоения - по закону косинуса, т.е. их векторы смещены на 90 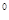 . Поэтому их суммарное воздействие на прибор можно записать как:
. Поэтому их суммарное воздействие на прибор можно записать как:
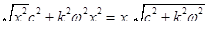 .
.
Переходя к коэффициенту передачи силы, по аналогии с уравнением (3) получим:

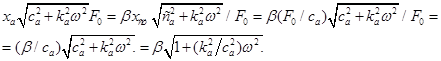 (4)
(4)
Введем известные обозначения ka / m =2ε , 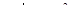 ,
,  , а также
, а также  и подставим их в выражение (4).
и подставим их в выражение (4).

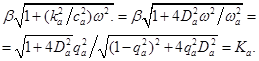 (5)
(5)
Это выражение называется коэффициентом амортизации. Очень часто коэффициентом амортизации называют и отношение амплитуды вынужденных колебаний прибора на амортизаторах к амплитуде колебаний основания, к которому прикреплены амортизаторы.
На рис.3 представлена зависимость коэффициента амортизации от отношения частот 
 и степени успокоения Da .Из выражения (5)легко найти значение qa , при котором коэффициент амортизации Ка меньше единицы, т.е. можно диапазон эффективной работы амортизатора, решив неравенство:
и степени успокоения Da .Из выражения (5)легко найти значение qa , при котором коэффициент амортизации Ка меньше единицы, т.е. можно диапазон эффективной работы амортизатора, решив неравенство:
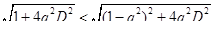
Результат решения  хорошо иллюстрируется графиком на рис.3. В диапазоне значений
хорошо иллюстрируется графиком на рис.3. В диапазоне значений  амортизатор обеспечивает уменьшение силы, действующей на прибор. С увеличением qa все кривые стремятся к нулю, т.е. эффективность амортизации возрастает. Из графика также видно, что при малых значениях qa значение Ка почти не отличается от единицы. При резонансе (qa=1) коэффициент Ка может возрасти до больших значений. Только введение в систему успокоителя позволяет значительно уменьшить резонансный пик. При резонансе коэффициент амортизации
амортизатор обеспечивает уменьшение силы, действующей на прибор. С увеличением qa все кривые стремятся к нулю, т.е. эффективность амортизации возрастает. Из графика также видно, что при малых значениях qa значение Ка почти не отличается от единицы. При резонансе (qa=1) коэффициент Ка может возрасти до больших значений. Только введение в систему успокоителя позволяет значительно уменьшить резонансный пик. При резонансе коэффициент амортизации
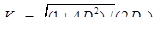
В этом случае желательно получить Ка более 1,5…2. Простой расчет показывает, что применение успокоения с Da=0,3…0,5 обеспечивает указанное значение коэффициента амортизации. С другой стороны, увеличение успокоения в диапазоне работы амортизаторов (при  ) ухудшает эффект амортизации. Тем не менее для защиты приборов, подверженных действию нестационарных сил, которые могут вызвать нежелательные свободные колебания, приходится идти на увеличение успокоения даже путем некоторого повышения коэффициента Ка в области высоких при степень успокоения приходится доводить до Da= 0,5. Исследования показывают, что при qa
) ухудшает эффект амортизации. Тем не менее для защиты приборов, подверженных действию нестационарных сил, которые могут вызвать нежелательные свободные колебания, приходится идти на увеличение успокоения даже путем некоторого повышения коэффициента Ка в области высоких при степень успокоения приходится доводить до Da= 0,5. Исследования показывают, что при qa 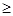 5 существенного улучшения амортизации не получается, поэтому обычно рекомендуют выбирать соотношение частот
5 существенного улучшения амортизации не получается, поэтому обычно рекомендуют выбирать соотношение частот  (Da=0) происходит уменьшения передаваемой силы на 80%, а при
(Da=0) происходит уменьшения передаваемой силы на 80%, а при  - на 95…96%. На графике логарифмической кривой представлена зависимость эффективности от соотношения частот qa при отсутствии успокоения (Da=0). Эффективность вычисляется по формуле
- на 95…96%. На графике логарифмической кривой представлена зависимость эффективности от соотношения частот qa при отсутствии успокоения (Da=0). Эффективность вычисляется по формуле 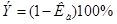 .
.
Прибор может испытывать со стороны основания и ударные воздействия. Примером такого воздействия может быть импульс силы – действие сравнительно большой силы в течение весьма малого промежутка времени. Ударное воздействие описывают уравнением 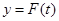 . Эта зависимость графически может быть представлена в виде кривых на рис.. Все указанные воздействия характеризуются формой кривой и длительного импульса tи. Для упрощения расчетов ударное воздействие часто заменяют одиночным импульсом синусоидальной полуволны (рис. ).
. Эта зависимость графически может быть представлена в виде кривых на рис.. Все указанные воздействия характеризуются формой кривой и длительного импульса tи. Для упрощения расчетов ударное воздействие часто заменяют одиночным импульсом синусоидальной полуволны (рис. ).
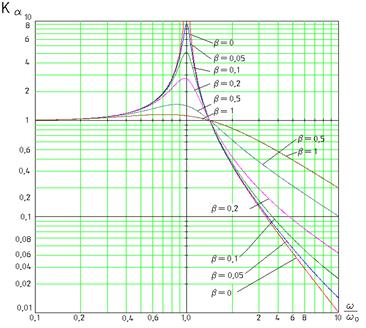
рис. 17
Контрольные вопросы
1. В каких случаях в приборах применяют амортизацию?
2. В чем разница между активной и пассивной амортизацией?
3. Что такое коэффициент динамичности амортизатора?
4. Как правильно подобрать коэффициент амортизации, чтобы избежать резонанса в приборе?
5. Какие достоинства и недостатки в конструкциях резиновых амортизаторов?
6. Какие достоинства и недостатки в конструкциях пружинных амортизаторов?
7. Какие достоинства и недостатки в конструкциях пружинно-фрикционных амортизаторов?
Конструкции амортизаторов.
В настоящее время применяются амортизаторы следующих типов:
- резиновые;
- пружинные;
- пружинно-резиновые;
- пружинно-фрикционные.
Наиболее простой конструкцией амортизатора является резиновая ножка (рис. 19). Суммарная жесткости четырех ножек равна 4c :
Из ранее приведенной формулы имеем:
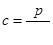
Отсюда:
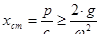 - проверка осадки
- проверка осадки

|
|
|
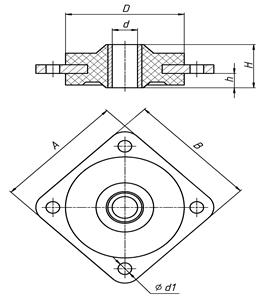
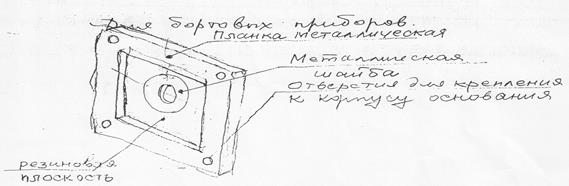
Резиновые амортизаторы, рис. 20 и рис. 21 нашли наиболее широкое применение. Резина в них служит одновременно и пружиной и хорошим успокоителем собственных колебаний вследствие большого внутреннего трения резины. Кроме того, резиновые амортизаторы имеют относительно небольшие размеры.
На рис. 22 показан амортизатор для бортовых приборов самолета. Здесь к центральному отверстию привинчивается один угол прибора, а всего их четыре, т.е. прибор подвешен на основании с помощью 4-х резиновых плоскостей (амортизаторов).
Пружинные амортизаторы с цилиндрической пружиной (рис. 22), применяют ограниченно, т.к. в них успокоение, получаемое в результате внутреннего трения материала пружины невелико, поэтому собственные колебания затухают медленно, а при резонансе амплитуды колебания прибора могут достигать больших величин.

рис. 22
На рис. 22: 1 – металлическая пружина; 2 – резина.
Особенность использования конических пружин заключается в том, что малые витки уходят внутрь, изменяется жесткость c. Особенность конструкции позволяет использовать конические пружины в качестве амортизаторов для полосы частот.
В резиновых амортизаторах в качестве упругого элемента используется резина, которая обладает хорошими упругими свойствами и высоким коэффициентом демпфирования из-за большого внутреннего трения. Кроме того, они компактны, легки и имеют небольшую стоимость. Основным недостатком указанных амортизаторов является зависимость упругих свойств резины от температуры окружающей среды и старение. При понижении температуры до 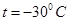 жесткость амортизаторов возрастает в 1,5 раза, а при
жесткость амортизаторов возрастает в 1,5 раза, а при 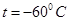 они практически не осуществляют виброзащиту. При высоких температурах (более
они практически не осуществляют виброзащиту. При высоких температурах (более 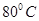 ) и солнечной радиации резина стареет и в ней образуются поверхностные трещины. Среднее значение деформации амортизаторов резиновых и резинометаллических
) и солнечной радиации резина стареет и в ней образуются поверхностные трещины. Среднее значение деформации амортизаторов резиновых и резинометаллических  при
при 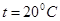 , а следовательно,
, а следовательно,  (
(  ).
).
Пружинные амортизаторы свободны от недостатков, свойственных резиновым и резинометаллическим амортизаторам. Однако их применение ограниченно, так как. у них собственное затухание (успокоение) невелико из-за малого внутреннего трения в материале пружины. Поэтому, собственные колебания в таких амортизаторах затухают медленно, а при резонансе колебания амортизируемого прибора могут быть значительны. Поэтому при использовании пружинных амортизаторов в систему виброзащиты необходимо вводить успокоитель.
Общим недостатком резиновых, резинометаллических и пружинных амортизаторов является то, что необходимое качество виброизоляции для каждого амортизатора обеспечивается лишь при определенной нагрузке и частоте внешних воздействий. Пружинные амортизаторы с демпфированием (равночастотные), изготовленные на основе конических пружин, обеспечивают необходимое качество виброзащиты при изменении частоты внешних воздействий и нагрузок в более широких пределах.
В амортизаторах с воздушным демпфированием (b =0.3…0.5), амортизатором является спиральная пружина 1. При увеличении нагрузки витки пружины осаживаются на опорную поверхность 2 и выключаются из работы. Это приводит к повышению жесткости амортизаторов к сохранению частоты собственных колебаний. Наличие резинового баллона 3 с калиброванным отверстием создает дополнительное затухание.
ЛЕКЦИЯ № 31
Демпферы
В приборе, изображенном на рисунке, подвижная система 1 выведена из равновесия и совершает колебания относительно неподвижного корпуса 2. Возникновение собственных колебаний системы 1 препятствует быстрой обработке сигнала измеряемой величины.
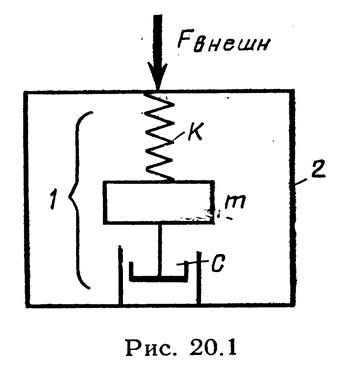
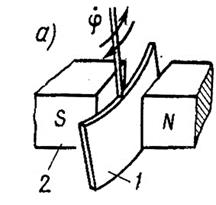
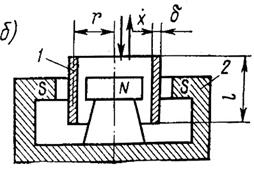
Рис.14.1 Рис.14.2
Успокоитель (демпфер) – устройство, предназначенное для уменьшения продолжительности колебаний подвижной системы прибора около точки установившегося отклонения.
Демпферы
ЛЕКЦИЯ № 33
Амортизаторы.
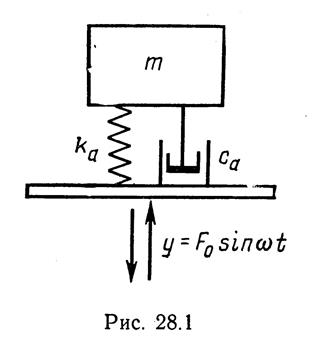
Колебательное движение основания (объекта), на котором укреплен прибор, можно описать функцией, изменяющейся во времени.
Например, 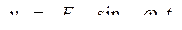
Дифференциальное уравнение движения прибора на амортизаторах:
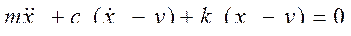 ,
,
где m - масса прибора; xa - смещение прибора относительно основания;
ca - коэффициент успокоения, создаваемого в амортизаторе; y - смещение основания; ka - коэффициент жесткости амортизатора.
Решение уравнения при синусоидальном законе движения основания:
 ,
,
где x 0 - начальный размах колебаний прибора на амортизаторе;
ε - половина удельного коэффициента успокоения в системе «прибор-амортизатор»;
ω a - частота собственных колебаний прибора;
γ a и γ1 - начальные фазы; β - коэффициент динамичности;
x ст - статическая деформация амортизатора под действием веса прибора.
Первое слагаемое описывает свободные затухающие колебания, второе слагаемое -движение самого прибора.
При отсутствии успокоения в системе амортизации (са = 0)
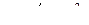 ,
,
где 
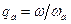 - отношение угловых частот вынужденных и собственных колебаний. На рис. показана зависимость коэффициента динамичности β от qa.. Коэффициент динамичности показывает, во сколько раз изменяется амплитуда вынужденных колебаний прибора, установленного на амортизаторе по сравнению с амплитудой колебаний основания:
- отношение угловых частот вынужденных и собственных колебаний. На рис. показана зависимость коэффициента динамичности β от qa.. Коэффициент динамичности показывает, во сколько раз изменяется амплитуда вынужденных колебаний прибора, установленного на амортизаторе по сравнению с амплитудой колебаний основания:
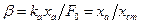 .
.
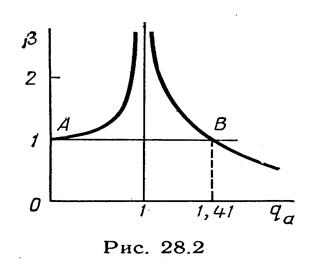
В точке 1 передаваемая сила равна возмущающей, а это значит, что прибор жестко прикреплен к основанию. Анализ графика показывает, что коэффициент жесткости должен быть такой, чтобы угловая частота ω a собственных колебаний прибора на амортизаторе была мала по сравнению с угловой частотой ω возмущающей силы. График также показывает, что если отношение частот qa < 1,41 (точка В), то амортизатор увеличивает передаваемую силу.
ЛЕКЦИЯ№30
Потенциометры
Потенциометры предназначены для получения электрического сигнала функционально зависящего от перемещения токосъёмного элемента. Потенциометр представляет собой регулируемый делитель напряжения, выполненный на основе резистивного элемента.

Рис.30.1.
Конструкция линейного потенциометра представляет собой жесткий каркас 1 постоянного поперечного сечения, выполненный из токонепроводящего материала. На каркас намотана проволока 5 (резистивный элемент), от которого в точках А и В сделаны два отвода 6. По зачищенной от изоляции контактной дорожке перемещается подвижный контакт 4, связанный с движком 2. От подвижного контакта 4 сделан отвод 3. Полная рабочая длина потенциометра меньше длины намотки. Это сделано для того, чтобы не происходило размыкание контакта 4 при выходе движка за расчетные пределы.
В соответствии с обозначениями электрической схемы входное напряжение подводится к точкам А и В, а выходное напряжение снимается с участка между точками А и С. Связь между омическим сопротивлением обмотки Rx c перемещением движка lx:
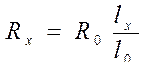 ,
,
где R 0  - полное сопротивление потенциометра.
- полное сопротивление потенциометра.
Выходное напряжение на линейном потенциометре:
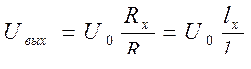

Зависимость U вых = f ( lx ) – характеристика потенциометра;
если зависимость Rx = f ( lx ) линейна, то потенциометр линейный;
если зависимость Rx = f ( lx ) нелинейна – функциональный потенциометр.
 Параметры потенциометров:
Параметры потенциометров:
|
2) мощность;
 3) предельное рабочее напряжение;
3) предельное рабочее напряжение;
|
перемещение движка;
5) момент трогания.
Характеристики потенциометра
1. Разрешающая способность - определяется витковой погрешностью.
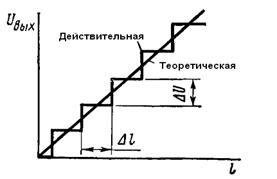
В проволочных потенциометрах равномерное перемещение движка приводит к дискретному изменению U вых . Это связано с переходом движка с одного витка на другой.
Величина Δ U обратно пропорциональна числу витков:
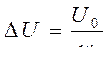
Δ U обусловливает витковую погрешность.
Витковая погрешность δв – наибольший отклонение U вых (зависит от теоретической характеристики). Величина этого отклонения равна Δ U /2.
В процентах U 0 % витковая погрешность δв равна: δв = (1/2 w )·100%.
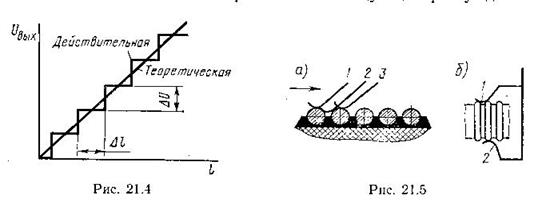
2. Общее сопротивление R 0 – зависит от геометрических размеров потенциометра и параметров обмотки (R 0 ограничивается снизу допустимым нагревом и точностью, а сверху – технологическими возможностями).
На характеристику потенциометра оказывает влияние сопротивление нагрузки R н .
При Rн = ∞, 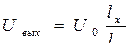
При Rн ≠ ∞, 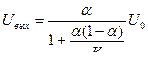 , где
, где 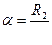 , К = R н / Ro .
, К = R н / Ro .
Погрешность δн от нагрузки равна
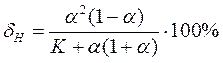
Погрешность δн тем больше, чем меньше K, следовательно К необходимо увеличивать, например, за счёт уменьшения R о .
3. Действительная мощность потенциометра P.
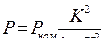 , где
, где 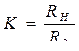
Номинальная мощность рассеяния P ном – величина мощности, которая может рассеиваться без ухудшения его характеристик.
Величина мощности позволяет определить максимальное допустимое значение U 0 max:
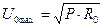
Действительная мощность рассеяния:
при R н = ∞, P ном = U 0 2 / R 0;
при R н ≠ ∞, 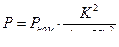 ; К = R н / Ro;
; К = R н / Ro;
при R н = R 0 (К = 1); P = 0,25۰P ном
4. Допустимая скорость перемещения движка не больше чем
100÷150 об/мин.
5. Рабочий вращающий момент; в проволочном потенциометре общего назначения 5 ÷ 36 Нмм.
Конструкция
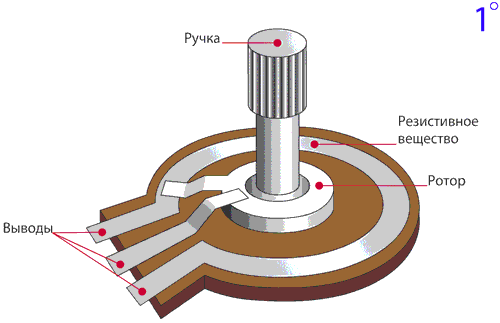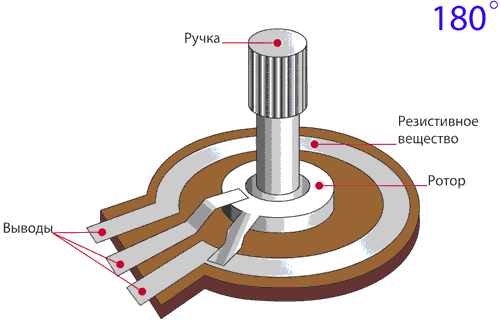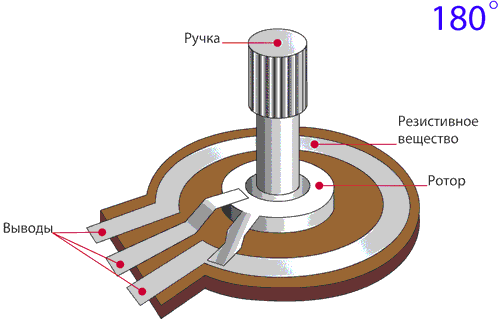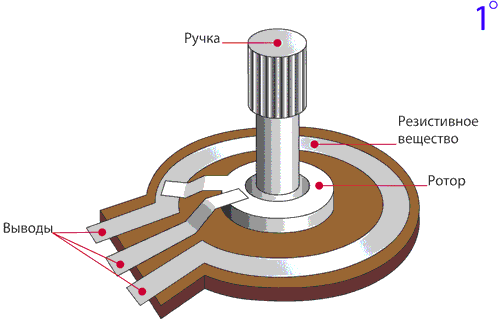
Каркасы: кольцевые (а), пластинчатые (б), стержневые (в), дуговые (г), многооборотные (д)
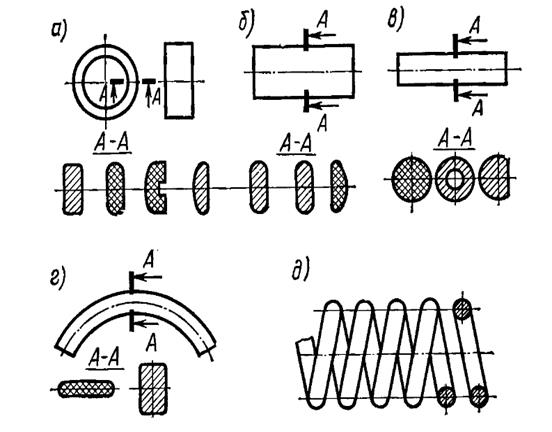
Рис.
Материалы: гетинакс марок B, Bв, Бв; текстолит марок ПТК, B4; пресспорошки марок К+18-2, К+21-22, АГ-4; алюминиевые сплавы АMг, Д16.
Изоляционная плёнка у металлических каркасов получается либо нанесением лака, либо анодированием с последующей пропиткой лаком.
При конструировании особое внимание следует обращать на выполнение выводных концов.
Для подсоединения выводного провода применяются пайка и сварка. Припой ПОС-40, ПОС-61; для нихрома – ПСр 25, ПСр 45. Из технологических соображений при диаметре проволоки d = 0.03…0.3 мм толщину каркаса следует брать > 4d; радиусы закругления > 2d .
Требования к проволоке:
1) высокое удельное сопротивление,
2) малый температурный коэффициент электрического сопротивления,
3) высокая коррозионная стойкость,
4) высокая прочность и износостойкость.
Материалы проволоки: константан, манганин, нихром, платина-иридий, платина – никель, палладий – серебро, золото – никель.
Расчёт потенциометров
Расчёт линейного потенциометра заключается в определении диаметра намоточного провода и геометрических размеров каркаса.
Обычно заданы: R 0 , U 0 , R н , δв допустимые габариты, условия эксплуатации.
1. Определяется P ном = U 0 2 / R 0; зная схему включения, определяется действительная мощность рассеяния P .
2. Вычисляется диаметр проволоки по формуле: 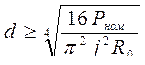
значения диаметра округляется в сторону увеличения до стандартного.
3. Определяется длина провода
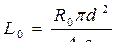 , где ρ – удельное сопротивление в Ом۰м
, где ρ – удельное сопротивление в Ом۰м
4. Вычисляется средняя длина витка lср = L/w;
при прямоугольном каркасе 
5. По средней длине витка выбирают число витков 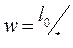 ,
,
где l0 - рабочая длина обмотки; t - шаг намотки.
Выбор диаметра проволоки d определяется тепловым режимом по допустимой плотности тока j:
· для каркасов из пресспорошка j = 10 А/мм2;
· для металлических каркасов j = 30 А/мм2;
· для благородных металлов j = 50 А/мм2;
· с охлаждением j = 80 ÷ 100 А/мм2.
Значения диаметров проволоки выбираются из интервала: d = 0,03÷0,3 мм.
Для устранения влияния нагрузки линейный потенциометр проектируют как функциональный. Например, можно применять схемы с дополнительным сопротивлением или шунтом.
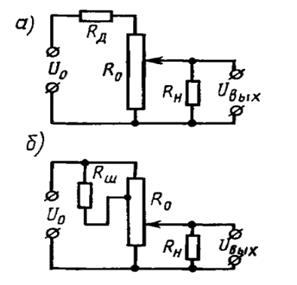
Подключение шунта наиболее эффективно в точке α = 0,74. Шунт должен иметь сопротивление Rш = 0,31Rн.
Электрические контакты.
Электрические контакты представляют собой конструктивно оформленные соединения токоподводящих частей.
Классификация
По функциональному признаку:
1. Неразъемные - пайка, сварка, обжатие и в виде зажимов.
2. Разъемные - штепсельные разъемы и другие виды разъемов.
3. Разрывные контакты – реле;
состояния: замкнутое - размыкание или разомкнутое - замыкание.
4. Скользящие - потенциометры и коллекторы.
Основное требование:
качество мест соприкосновения токоподводящих частей должно быть таким, чтобы контакты не оказывали влияния на параметры передаваемого сигнала.
В зависимости от формы поверхностей соприкосновения:
1) точечные - при малых токах и небольших контактных усилиях;
2) линейные - от нескольких ампер до десятков ампер;
3) плоскостные - обладают большой надежностью.
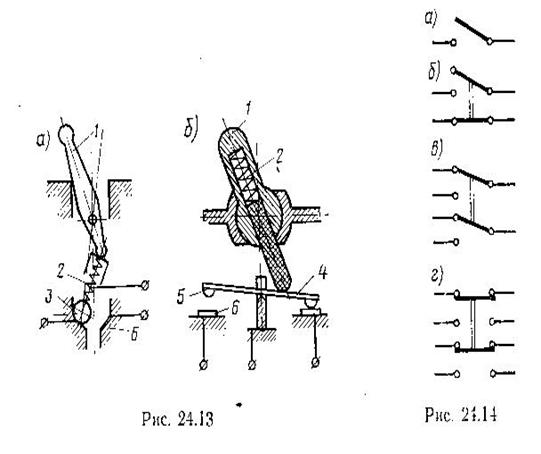
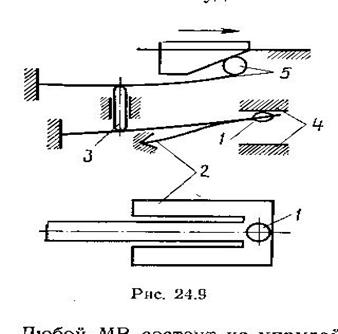
Размыкание контактов.
Характеризуется электрическим износом (эрозией) контактов, вызванным газоразрядными процессами. Вид газового разряда зависит от типа и параметров коммутируемой цепи, состояния поверхности и материалов контактов, расстояния между контактами, состава и состояние среды, в которой происходит размыкание.
В первый момент при размыкании происходит уменьшение числа контактирующих точек и площадей их соприкосновения (когда Uк превышает Uк2 достигается температура плавления). Расплавленные контактные точки сливаются в каплю жидкого металла, образуя жидкий мостик между анодом и катодом
- мостиковая эрозия анода. Мостиковая эрозия зависит от тока, материалов контактов и параметров окружающей среды.
Это явление предшествует газоразрядным процессам в зазоре.
Если U > U0 и I > I0 (для данного зазора δ) - то образуется электрическая дуга, где U0 и I0 – напряжение и ток дугообразования для данных материалов контактов.
Если известны вольтамперные характеристики дуги при различных δ, то зная U и R в цепи, можно графическим построением выбрать значение δ, достаточное для самогашение дуги. Гашение дуги при переменном токе осуществляется легче, чем при постоянном.
Вредное воздействие оказывает искра и поэтому необходимо применение схем искрогашения.
Разомкнутое состояние
Требование к контактам:
· большая изоляционная прочность контактного промежутка.
· необходимость обеспечить такой зазор δ, чтобы не произошел пробой при проверке электрической прочности изоляции в приборном устройстве.
Однако чрезмерное увеличение δ нежелательно, так как это ведет к дребезгу при замыкании, увеличению времени срабатывания и снижению ресурса контактирующей системы.
Замыкание контактов
Соединение контактов представляет собой ударный процесс, при котором происходит многократный переход кинетической энергии подвижных частей в потенциальную энергию упругих элементов контактной системы и обратно, пока излишек кинетической энергии не рассеется. Это приводит к вибрации контактов (дребезгу). Дребезжание сопровождается разбрызгиванием расплавленного материала. Износ контактов при замыкании может оказаться больше, чем при размыкании.
Дребезжание зависит от многих причин: свойств материалов, соотношения масс подвижных и неподвижных элементов, скорости движения подвижной системы и др.
Уменьшение дребезга:
а) уменьшение массы и скорости подвижной системы;
б) обеспечение интенсивного рассеивания энергии в момент замыкания путем увеличения гистерезисных потерь, увеличения сухого трения, снижения твердости материалов контактов, применения гасителей вибрации;
в) увеличение контактных усилий.
Материалы контактов
Требования:
1) низкое удельное сопротивление ρ0;
2) низкий температурный коэффициент сопротивления;
3) высокая удельная теплопроводность;
4) высокая износостойкость;
5) высокая температура плавления;
6) неокисляемость и антикоррозийность;
7) малая твердость, для улучшения условий замыкания;
8) хорошие технологические свойства.
Применяются материалы: медь, серебро, платина, палладий, золото, вольфрам и их сплавы с другими металлами и окислами.
Форма контактов выбирается в зависимости от характера эрозии, волн передаваемого тока, усилий в контактной паре, теплового режима работы контактов.
Скользящие контакты
Скользящий контакт должен обеспечивать непрерывные замыкания электрической цепи, в противном случае возникают электрические шумы.
Для скользящих контактов используют латунь, бронзу, серебро, золото платину, палладий. В электрических машинах медно-графитовые контакты.
Контактное сопротивление может быть представлено следующей формулой:
R к = R 0 + R пер + R пл R 0 << R пер + R пл
R0-сопротивление контактов (материалов);
Rпер-переходное сопротивление, вызванное наличием микронеровностей на поверхности контактов;
Rпл-пленочное сопротивление.
Основными факторами, влияющими на Rк, являются величины контактного усилия P и тока I, протекающего через контакт, а также механические электрические свойства материалов контактов и поверхностных пленок.
Для получения Rк наиболее часто используют формулу:
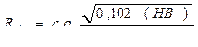
где с - коэффициент шероховатости поверхности;
с =3 - для очень грубых поверхностей;
с =2 - для грубых поверхностей;
с =1 – для чисто обработанных поверхностей.
b – коэффициент, зависящий от характера деформации, вида и формы зоны контакта;
b = 0.33 - при нагрузке ниже предела упругости;
b = 0.5 - при нагрузке выше предела упругости;
b = 0.7…1.0 – при отсутствии изолирующей плёнки;
b = 2 - при плоскостном контакте.
P - контактное усилие (Н).
HB - твердость по Бринелю наиболее мягкого материала (Н/см²)
Формула справедлива для не нагретых контактов. Большое влияние на величину Rк независимо от усилия Р оказывает напряжение Uк в контакте. При Uк1 –температура достигает температуры рекристаллизации и происходит резкое уменьшение механической прочности материала. Uк2 – температура достигающая температуры плавления.
ЛЕКЦИЯ № 29
Электромагнитные механизмы
Электромагнитными механизмами (ЭММ) называются механизмы, в которых для осуществления перемещения рабочего органа используются электромагнитные силы. ЭММ применяются в приборостроении в качестве различных электромагнитных контактных и релейных устройств, вибраторов, клапанов, арретиров, датчиков углового и линейного перемещения, датчиков сил и моментов. Особенно часто применяются в гироскопической технике, где механические элементы стали основными источниками погрешностей.
В последнее время ЭММ стали вытеснять обычные механические элементы, такие, как зубчатые и фрикционные передачи, опоры качения и скольжения.
ЭММ весьма разнообразны как по используемым принципам действия, по назначению, так и по конструктивным решениям.
Классификация ЭММ
1. В зависимости от способа создания магнитного потока и характера
действующей намагничивающей силы:
а) нейтральные постоянного тока;
б) поляризованные постоянного тока;
в) переменного тока.
В ЭММ постоянного тока рабочий поток создается с помощью катушек, подключенных к источнику постоянного тока. Действие нейтральных ЭММ зависит только от величины тока, протекающего по катушке, и не зависит от его направления.
Поляризованные ЭММ характеризуются наличием двух независимых магнитных потоков: поляризующего и рабочего. Поляризующий поток создается обычно постоянным магнитом (иногда электромагнитом). Действие поляризованного ЭММ зависит как от величины, так и от направления постоянного тока протекающего в рабочей катушке.
В ЭММ переменного тока рабочий магнитный поток изменяется по величине и направлению, создавая электромагнитную силу, пульсирующую от нуля до максимума, с удвоенной частотой по отношению к частоте питающего тока.
По характеру работы катушек ЭММ делятся на работающие:
а) в длительном режиме;
б) в прерывистом режиме;
в) в кратковременном режиме.
По скорости действия :
а) с нормальной скоростью;
б) быстродействующие;
в) замедленно действующие.
Это разделение весьма условное и свидетельствует о том, приняты ли специальные меры для получения необходимой скорости действия.
По способу включения катушек:
а) с параллельным включением;
б) с последовательным включением.
В зависимости от расположения подвижного элемента (якоря) относительно остальных частей ЭММ:
а) с внешним притягивающимся якорем (клапанные);
б) с втяжным якорем (плунжерные);
в) с поперечно движущимся якорем.
Несмотря на большое разнообразие ЭММ – механизмы состоят из основных частей одноименного назначения.
Основные части ЭММ
Конструктивные типы ЭМ и их особенности.
Существующие в настоящее время ЭМ характеризуются большим разнообразием конструктивных форм магнитопровода, количеством и расположением катушек и т. д.
Их классифицируют по следующим наиболее важным признакам:
· по характеру движения якоря — с прямоходовым и с поворотным якорем;
· по форме магнитопровода — с магнитопроводом Ш-образным, U-образным или подковообразным, цилиндрическим и т.д.,
· по расположению якоря относительно намагничивающей обмотки - с внутренним, или втягивающимся, якорем, который в этом случае иногда называют плунжером, и с внешним, или притягивающимся, якорем - клапаном.
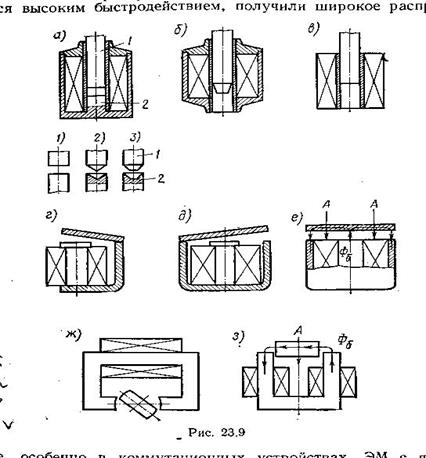
Последние, в свою очередь, подразделяются на ЭМ с внешним притягивающимся якорем (якорь движется в направлении магнитного потока Фδ, и ЭМ с якорем, движущимся поперек направления потока Фδ . ЭМ с втягивающимся якорем называют иногда соленоидными или плунжерными, а ЭМ с внешним притягивающимся якорем - ЭМ клапанного типа.
Основные конструктивные типы ЭМ изображены на рис.

1 - якорь
2 – стоп
3 - катушка
4 - неподвижная часть магнитопровода
5 - направляющая движения якоря
6 - каркас катушки
7 - рабочий зазор
На рис. 23.6, а элементы неподвижной части имеют следующие названия: 1 — ярмо (корпус, скоба), 5 — полюсный наконечник или шляпка,
7 — сердечник.
Магнитная цепь — это совокупность всех элементов, через которые замыкается магнитный поток. Она включает участки, выполненные из ферромагнитных материалов, и воздушные зазоры.
Конструктивно ЭМ состоит из двух основных частей: катушки с расположенной на ней обмоткой 6 (ЭМ может иметь несколько катушек и несколько обмоток) и магнитопровода — элементов из ферромагнитных материалов.
Обмотка в ЭМ служит для создания намагничивающего поля, а магнитопровод — для его усиления и проведения результирующего магнитного потока. Магнитопровод включает подвижный элемент 3, называемый якорем, и неподвижную часть. Неподвижная часть в зависимости от конструктивного исполнения и формы может носить разные названия, причем состоять из нескольких деталей (основания, корпуса, фланцев и т. д.).
Сердечником называют часть магнитопровода, находящуюся внутри катушки. Иногда роль сердечника выполняет якорь. Якорь отделяется от остальных частей магнитопровода воздушными зазорами и представляет собой элемент ЭМ, который, воспринимая электромагнитную силу, передает ее ведущему элементу ПМ ИЭММ. Количество и форма воздушных зазоров, отделяющих якорь от неподвижной части магнитопровода, зависят от конструкции ЭМ. Воздушные зазоры, в которых возникает полезная сила, называют рабочими 4 ; зазоры, в которых не возникают силы в направлении возможного перемещения якоря, называют паразитными (8 на рис.). Паразитные зазоры обусловлены технологическими факторами, а также необходимостью исключения залипания якоря от остаточной намагниченности при отключении ЭМ. Их размер колеблется от сотых до десятых долей миллиметра.
Для характеристики магнитного поля вводят понятия магнитного потока Ф [Вб], и его интенсивности или плотности В [Тл], которую называют магнитной индукцией.
В соответствии с определением: В = Ф/ S.
В качестве основных величин магнитного поля чаще всего принимают индукцию В и магнитную постоянную μ0 [Гн/м], или абсолютную магнитную проницаемость μ [Гн/м], причем индукция рассматривается как величина, характеризующая силовые возможности поля. Для удобства выполнения расчетов в дополнение к основным величинам В и μ0 формально вводят вспомогательную величину — напряженность поля Н [А/м], не давая ей физического толкования: Н = В/ μ, где μ = μr μ0, μ0 = 4π ۰10-7 [Гн/м], а μr - относительная магнитная проницаемость среды. При расчете ЭМ условно принимают, что для воздуха. и неферромагнитных материалов μr = 1; для магнитно-мягких материалов порядок расчетных значений величины Н обычно от десятков до тысяч А/м, а В — от десятых долей до 1,5... 2,0 Тл.
Источник магнитного поля характеризуется магнитодвижущей силой (МДС) обмотки:
Fт = I ∙ w , где I — сила тока в обмотке, w — число ее витков.
При анализе рабочего процесса в ЭМ кроме перечисленных характеристик магнитного поля пользуются также такой характеристикой, как потокосцепление намагничивающей обмотки ψ, которое равно алгебраической сумме потоков, пронизывающих отдельные витки обмотки ψ = Ф1+Ф2+…+Ф n. .
Если все витки обмотки w сцепляются с одним и тем же потоком Ф,
то ψ =w ∙Ф, если же они пронизываются разными потоками, причем известно изменение потока вдоль оси обмотки, которая является равномерно распределенной по длине, то ψ =w ∙Фср, где Фср – среднее значение потока по длине обмотки.
Часть полного магнитного потока Ф, которая проходит через рабочий зазор δ , называется рабочим магнитным потоком и обозначается Фδ. Часть потока Ф, которая не замыкается через рабочий зазор, называется потоком рассеяния или потоком утечки и обозначается Фs или Фy. Поверхности магнитопровода, ограничивающие рабочий зазор, называют полюсами 2.
Динамический режим работы ЭММ определяется общим уравнением сил
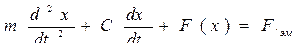
Левая часть уравнения представляет собой сумму сил сопротивления,
правая - движущую силу. В первом приближении инерционными силами можно пренебречь, тогда F(x) = Fэм. Тогда в левой части остаются механические силы сопротивления движению. Они зависят от перемещения якоря x.
Если воспользоваться обозначением величины зазора δ , то можно записать
F мех = f (δ) - эта зависимость называется механической характеристикой ЭММ.
Движущая сила также зависит от зазора Fэм= f2(δ) – эта зависимость называется статической тяговой характеристикой ЭММ.
Движение якоря возможно, когда F эм > F мех. .
Таким образом, механическая и тяговая характеристики должны быть согласованы.
Механическая характеристика, или характеристика противодействующих сил (нагрузки) - это зависимость полной силы (момента) сопротивления, приведенной к якорю, от его положения или размера рабочего зазора: F мех = f (δ).
Силы сопротивления включают силы полезной нагрузки, приложенные к конечному элементу передаточного механизма (с ними связано выполнение полезной работы), а также силы вредного сопротивления, к которым относятся силы трения, действующие на подвижные элементы, и сила возвратной пружины.
Тяговая характеристика - зависимость электромагнитной силы притяжения, действующей на якорь, от его положения или размера рабочего зазора F эм = f (δ). Различают статическую тяговую характеристику, если она рассматривается при постоянных значениях питающего тока (или напряжения),
т. е. при I = const (или U = const), и динамическую тяговую характеристику, учитывающую, в отличие от статической, изменение тока в обмотке ЭМ при движении якоря.

В силу разного характера изменения тока в режиме включения и отключения ЭММ динамические тяговые характеристики для этих режимов также различны. Взаимное расположение тяговых и механических характеристик показано на графике. На графике тяговая сила должна лежать выше механической. Якорь перемещается поперек магнитных силовых линий, поворачиваясь вокруг своей оси развивают сравнительно малые усилия, но позволяют путем согласования формы подвижного элемента менять в широких пределах тяговую характеристику.
Для надежного срабатывания ЭММ при включении необходимо, чтобы динамическая тяговая характеристика 2 во всем диапазоне изменения зазора δ проходила выше механической характеристики 3, а для четкого срабатывания ЭММ при отключении, наоборот, динамическая характеристика 4 должна проходить ниже механической. Обеспечение при расчете ЭММ необходимого взаимного расположения тяговой и механической характеристик называют их согласованием. Обычно ограничиваются согласованием статической тяговой 1 и механической 3 характеристик, поскольку построение динамической тяговой характеристики связано с определенными трудностями. При этом учитывают то обстоятельство, что динамическая тяговая характеристика 4 лежит ниже статической 1.
Материалы магнитопривода
Для изготовления магнитопривода ЭММ применяются преимущественно магнитомягкие материалы. Они характеризуются высокой магнитной проницаемостью μ и низкой коэрцитивной силой Hc . От правильного выбора материала во многом зависит качество конструкции ИЭММ в целом.
Применяют: низкоуглеродистые электротехнические стали марок Э, ЭА и ЭНА
(Hc =80 а/м, Вмах=1,5... 2 тл), кремнистые легированные стали марок Э11, Э21, Э31, Э41 (Нс=1,00…50 а/м), электротехнические х/к стали Э310, Э330, Э340 (μ=103); железоникелевые сплавы (пермаллой) : 50Н, 50НХС
(Нс=10…20 а/м, Вмах=1,5 тл, μ=(2... 5)*104) и с высоким содержанием никеля 79НН, 79НМА, 80НХС (Нс=1... 3 а/м, Вмах=0,75 тл, μ=105). Пермаллой обладает большим электрическим сопротивлением, имеет высокую μ, очень малую коэрцитивную силу Нс, т.е. малые потери на гистерезисе. Основной недостаток – невысокая Вмах.
В последнее время в приборостроении и автоматике широко используются ферриты и магнитодиэлектрики, представляющие собой ферромагнитный материал, получаемый спеканием порошковой металлургии.
Характеристики ЭММ
Основными характеристиками
ЭММ являются тяговая и механическая силы.
1) механическая характеристика – зависимость Fмех= f1(δ).
2) тяговая характеристика – зависимость Fэм= f2(δ)
Кроме основных:
3) нагрузочная характеристика – связывающая значение ЭМ силы с величинами Uэм, или Ìэм, при δ = const. Fэм = f ( U ); Fэм = f (Ì)
4) условная полезная мощность (P n)усл = Fэ δ max (δmax – δmin) при Ì = const
5) время срабатывания tср
6) характеристика нагрева vобщ = f(t)
Характеристика нагрева - зависимость температуры нагрева обмотки ЭМ от продолжительности включенного состояния ν = ν( t ).
Прочие характеристики и параметры: масса, габариты, потребляемая мощность, показатели эффективности и т. д.

Построение механической характеристики .
Для построения механической хар-ки весь путь якоря разбивают на отдельные участки и для каждого из них определяют величину сил, преодолеваемых якорем при притяжении. Сделать это можно либо расчетным путем, либо экспериментальным, т.е. непосредственным измерением этих сил с помощью граммометров, ньютометров и т. д.
ЛЕКЦИЯ №31
Кулачковые механизмы
31.1. Основные сведения
Кулачковая передача состоит из кулачка и толкателя. Чаще ведущим кинематическим звеном кулачковой передачи является кулачок. Кулачковые передачи преобразуют движение кулачка в поступательное движение или качание толкателя. Кулачковые передачи находят широкое применение в приборных устройствах и машинах, в различных автоматических, счетно-решающих, распределительных устройствах двигателей и станков-автоматов. Операционные кулачковые передачи используют для зажима деталей, возврата стрелок шкальных приборов на ноль, замыкания электрических контактов в электрических переключателях и при обработке деталей по копиру, фиксации взаимного положения деталей и узлов. Функциональная кулачковая передача служит для воспроизведения заданной функции. Большинство функциональных передач позволяет осуществить зависимость у = f (х). Перемещение кулачка, как и перемещение толкателя, может быть или линейным, или угловым.
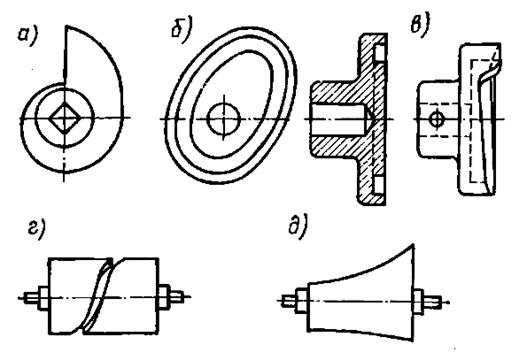
рис. 31.1
На рис. 31.1 показаны некоторые конструкции кулачков, которые применяются наиболее часто; а — плоский дисковый кулачок, б— торцовый кулачок с канавкой, в — торцовый кулачок без канавки, г — цилиндрический кулачок с канавкой, д — коноид. Кулачковый механизм с коноидом позволяет осуществить зависимость z = f (х, y ), где х пропорционально углу поворота коноида, у пропорционально перемещению коноида вдоль оси его вращения, z пропорционально перемещению толкателя. Радиус-вектор коноида изменяется не только при его вращении, но и при перемещении вдоль оси вращения.
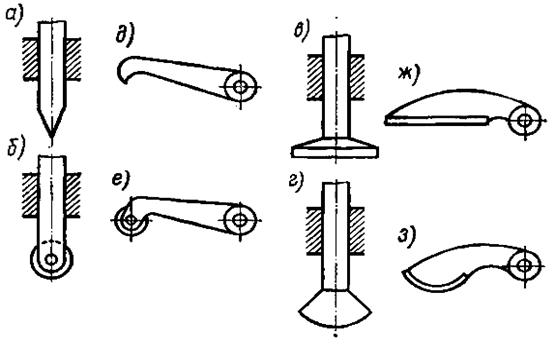
рис. 31.2
Заостренные толкатели (рис. 31.2, а, д) применяют только при небольших усилиях. Практически конец заостренного толкателя всегда имеет небольшое закругление. Часто используют толкатели, у которых имеется значительный радиус закругления конца (рис. 31.2, г, з), а также плоские толкатели (рис. 31.2, в, ж). Плоский толкатель работает с выпуклым кулачком. При роликовых толкателях между кулачком и толкателем действует трение качения (рис. 31.2, б, е). Благодаря этому уменьшаются трение и износ. Толкатели на рис. 31.2, а...г двигаются поступательно, а толкатели на рис. 31.2, д...з поворачиваются.
Кулачковые передачи могут иметь силовое или кинематическое замыкание. При силовом замыкании толкатель прижимается к кулачку пружиной. На рис. 31.4, а - ж представлены различные вариации кулачковых механизмов с силовым замыканием, где обозначены:
1 — кулачок, 2 — толкатель, 3 — пружина.
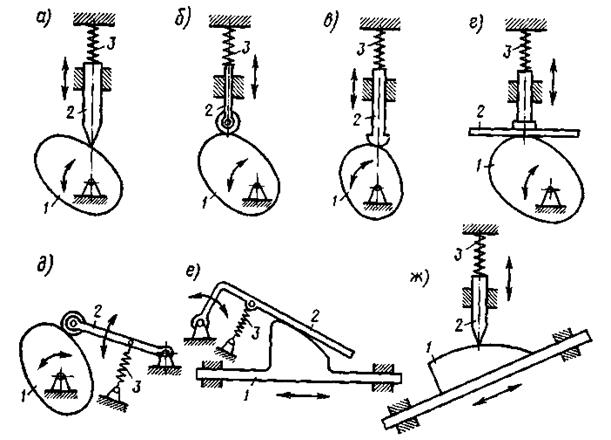
рис. 31.4
При кинематическом замыкании кулачкового механизма отпадает необходимость в пружине. Схемы кулачковых механизмов с кинематическим замыканием кинематической цепи показаны на рис. 31.5. При повороте торцового кулачка с канавкой (рис. 31.5, а) роликовый толкатель перемещается вверх или вниз вдоль своей направляющей, а ролик не выходит из канавки кулачка. Двойной дисковый кулачок (рис. 31.5, б) поворачивается относительно своей оси, вызывая угловое перемещение толкателя-коромысла. Ролики коромысла непрерывно касаются каждый своего кулачка. Поэтому профили обоих кулачков должны соответствовать один другому, что обеспечивается их построением. Хотя каждый из дисковых кулачков вместе со своим роликом составляет кулачковый механизм, требующий силового замыкания кинематической цепи, но их одновременное действие создает надежное кинематическое замыкание. При повороте цилиндрического кулачка с канавкой толкатель либо поворачивается (рис. 31.5, в), либо перемещается поступательно вдоль направляющей (рис. 31.5, г).
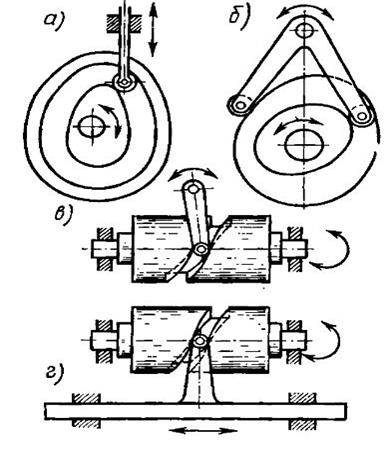
рис. 31.5
31.2 Кинематика кулачковых передач
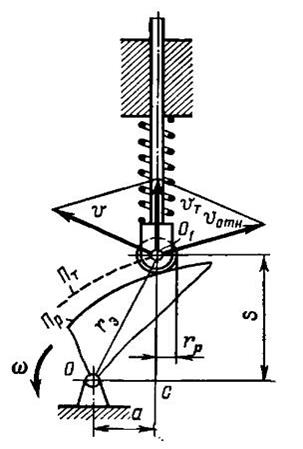
рис. 31.6
На рис. 31.6 показана кулачковая передача с поступательно перемещающимся дезаксиальным роликовым толкателем. Дезаксиальной эта передача называется потому, что средняя линия толкателя не проходит через геометрическую ось вращения кулачка О. Имеет место дезаксиал а = OC, причем OC перпендикулярно CO1. Кулачок вращается с угловой скоростью w. При этом геометрическая ось вращения ролика О1 перемещается по прямой вверх и все время находится на штриховой кривой, которая называется теоретическим профилем кулачка Пт. Длина пути s, проходимая толкателем, равна перемещению точки О1. Условно отсчитываем ее от точки С: 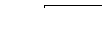 ,
,
где r э — радиус-вектор теоретического профиля Пт кулачка.
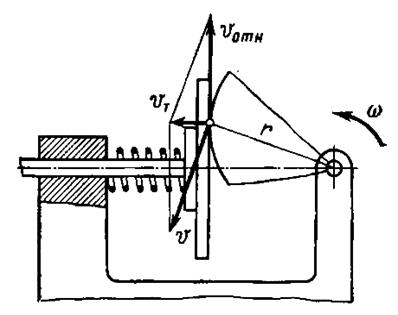
рис. 31.7
На рис. 31.7 построен план скоростей для центральной кулачковой передачи с дисковым кулачком и поступательно перемещающимся плоским толкателем. Окружная скорость кулачка перпендикулярна радиус-вектору r кулачка:
v = w r
Относительная скорость vотн, направлена по общей касательной, проведенной к поверхностям кулачка и толкателя в точке их касания. В данном случае она совпадает по направлению с плоскостью толкателя. Скорость толкателя vт направлена вдоль оси направляющей.
рис. 31.8
На рис. 31.8 показан план скоростей в кулачковом механизме с качающимся толкателем. Толкатель роликовый. Геометрическая ось вращения С ролика находится на теоретическом профиле Пт, кулачка. Реальный профиль Пр кулачка по отношению к теоретическому является эквидистантной кривой. Окружная скорость v перпендикулярна радиус-вектору rэ, а относительная скорость vотн касательна к теоретическому профилю в точке С. Окружная скорость vт толкателя перпендикулярна прямой O 2 C .
Программные механизмы
Кулачковые механизмы часто используют для смыкания и размыкания контактов. Программные механизмы обеспечивают размыкание групп контактов по определённой, заранее установленной, программе по времени. Набор кулачков из текстолита, установленных на общем валу, вращается с постоянной угловой скоростью w. Если кулачковый программный механизм совершает несколько оборотов, то программы повторяются. В этом случае программу указывают только для одного оборота и называют циклограммой. Заштрихованные участки соответствуют периодам замыкания, по горизонтали откладывается время (t), по вертикали количество кулачков (n).
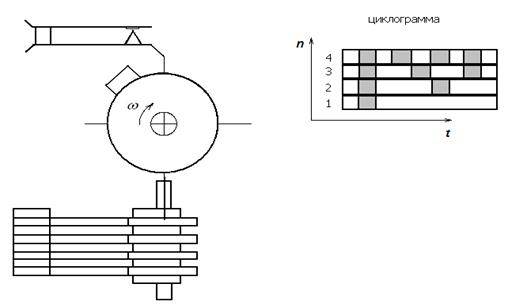
Силы в кулачковых передачах
На рис. 31.9 показаны силы в дезаксиальной кулачковой передаче с поступательно перемещающимся толкателем. Угол b между осевой линией толкателя и радиус-вектором, проведенным через точку касания толкателя и кулачка, называют углом толкателя. В общем случае угол b — переменная величина. Угол между линией действия силы F , приложенной к толкателю, и нормалью пп к поверхности кулачка в точке касания с толкателем называют углом давления a. Угол q между направлением радиус-вектора и нормалью к поверхности кулачка или линией действия нормальной силы Fn для той же точки называется углом кулачковой передачи или углом подъема кулачка.
Из треугольника ABE (рис. 31.10) получим формулу для определения угла передачи:
tg q = dr / ( rd g ),
где g — Угол поворота радиус-вектора кулачка.
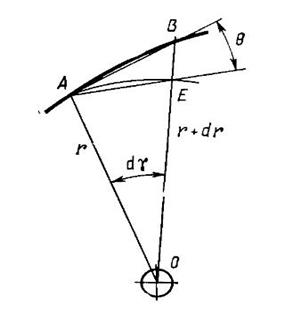
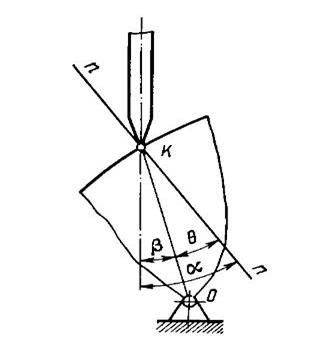
Треугольник ABE весьма близок к прямоугольному, причем угол ВЕА равен 90°. В этом легко убедиться, если учесть, что угол d g — бесконечно малая величина. Угол передачи может быть образован также касательной к поверхности кулачка и перпендикуляром к радиус-вектору, проведенному через точку касания. Из рис. 31.9 следует q = a ± b. Знак минус принимают, когда точка О находится правее линии действия силы F (рис. 31.11).
Для центрального кулачкового механизма
b = 0 и q = a
угол передачи в этом случае равен углу давления. Если не учитывать трения, то сила F, действующая на толкатель, вызовет нормальное давление
Fn = F / cos a
Сила трения, действующая на толкатель, равна
Fтр = f Fn
Равнодействующей сил Fn и Fтр является сила Fр. Угол между силами Fp и Fn равен углу трения j: f = tg j ,
где f — коэффициент трения между кулачком и толкателем. Увеличение угла давления при заданной силе F вызывает увеличение нормального давления Fn ,что способствует увеличению износа и потерь от трения. Сила Fр , действующая на толкатель, преодолевает силу пружины F и сопротивления от трения в направляющей. При значительных нагрузках реакции F 1 и F 2 возникают у краев направляющей. Они вызывают появление сил трения Fтрl = f1 F1 ; Fтр2 = f1 F2 ,
где f 1 — коэффициент трения между толкателем и направляющей.
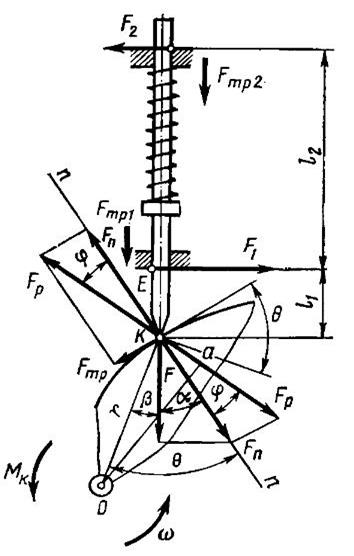
рис. 31.9
рис. 31.10 рис. 31.11
На рис. 31.3, а, б показано крепление роликов с подшипниками скольжения, на рис. 31.3, в, г — крепление роликов с подшипниками качения. Когда толкатель находится во взаимодействии с коноидом, то его конец имеет сферическую форму (рис. 31.3, д, е). Толкатель на рис. 8.3, д скользит по коноиду, а толкатель на рис. 31.3, е закреплен на подшипниках качения.
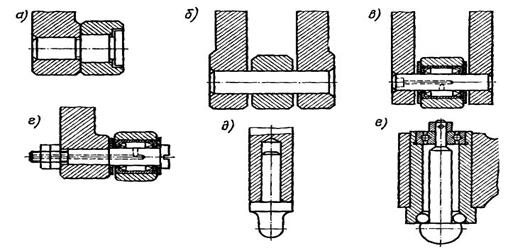
рис. 31.3
ЛЕКЦИЯ № 27
ЛЕКЦИЯ № 9
ЧЕРВЯЧНАЯ ПЕРЕДАЧА
Основные сведения. Классификация.
Червячные передачи применяют для передачи движения между перекрещивающимися осями. Угол перекрещивания может быть произвольным, но чаще используют угол равный 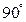 . По сравнению с зубчатыми передачами они дают возможность в больших пределах изменять угловые скорости. Червячная передача состоит из червяка, представляющего собой винт, и червячного колеса.
. По сравнению с зубчатыми передачами они дают возможность в больших пределах изменять угловые скорости. Червячная передача состоит из червяка, представляющего собой винт, и червячного колеса.

Обычно червячные передачи используют в качестве редукторов, когда движение передается от червяка к колесу, реже в мультипликаторах при обратной передаче (от колеса к червяку). В приборостроении применяются червячные передачи с эвольвентным профилем (даже в быстроходных механизмах при значительных нагрузках).
По форме поверхности, на которой образуется резьба, различают цилиндрические и глобоидные червяки (винт, нарезанный по поверхности тора).
В зависимости от формы профиля витка цилиндрических червяков различают:
- с архимедовым профилем (трапецеидальный в осевом сечении),
- с конволютным профилем (трапецеидальный в нормальном сечении),
- с эвольвентным профилем (в осевом сечении).
Дата: 2019-02-02, просмотров: 598.