Для проведения комплексной оценки хозяйственной деятельности предприятия сравнения по одному критерию явно недостаточно. В развернутом анализе экономические субъекты сравниваются сразу по нескольким критериям (например, по уровню рентабельности, оборачиваемости, росту продаж и т.д.). Многомерные сравнения необходимы для комплексной оценки результатов хозяйствования.
Комплексная оценка предполагает изучение совокупности показателей, которые дают многостороннюю характеристику изучаемого явления или объекта. Комплексная оценка применяется для анализа большинства экономических процессов, для исследования обобщающих данных о результатах деятельности предприятия.
При проведении в ходе комплексной оценки многомерных сравнений используются такие приемы, как построение многоосевых диаграмм показателей, методы ранжирования и расчета интегральных показателей, кластерный анализ (таксонометрический).
Последовательность оценки с использованием многоосевых диаграмм показателей следующая:
- выбираются критерии оценки;
- изображается окружность и наносятся оси для каждого критерия;
- выбирается область предпочтительных значений по построенным осям;
- фактические значения откладываются на осях и соединяются замкнутой линией.
В экономических исследованиях достаточно часто, приходится сталкиваться с проблемой группировки предприятий по нескольким признакам, для решения данной проблемы способы классических построений группировочных таблиц не приемлемы.
Пример 1
Имеются данные (табл.8.13.) по относительным показателям финансовой устойчивости и ликвидности предприятий. Изобразим их с помощью многоосевой диаграммы.
Таблица 8.13.
Показатели финансовой устойчивости и ликвидности предприятий
| Показатели | Рекомендуемые нормативы | Предприятие 1 | Предприятие 2 |
| Коэффициент абсолютной ликвидности | 0,2 | 0,3 | 0,1 |
| Коэффициент уточненной ликвидности | 0,8 | 1,0 | 0,8 |
| Коэффициент автономии | 0,5 | 0,8 | 0,6 |
| Коэффициент обеспеченности запасов и затрат собственными источниками финансирования | 0,7 | 0,8 | 0,5 |
| Коэффициент маневренности | 0,5 | 0,6 | 0,45 |
| Коэффициент устойчивости финансирования | 0,75 | 0,85 | 0,6 |
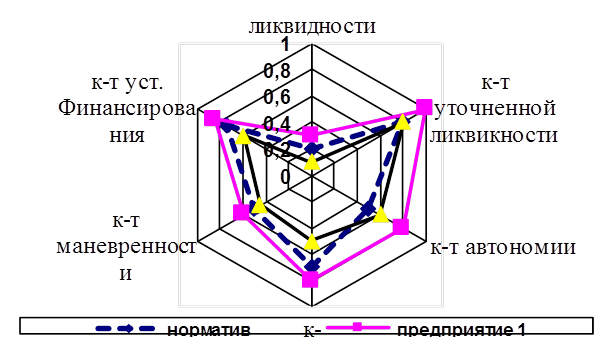 |
Рис. Пример многоосевой диаграммы
Кластерный анализ – один из методов многомерного анализа, предназначенный для группировки совокупности, элементы которой характеризуются многими признаками. Значения каждого из признаков служат координатами каждой единицы изучаемой совокупности в многомерном пространстве признаков. Каждое наблюдение, характеризующиеся значениями нескольких показателей, можно представить как точку в пространстве этих показателей, значения которых рассматриваются как координаты в многомерном пространстве.
Рассмотрим алгоритм кластерного анализа:
- от исходной совокупности наблюдений осуществляется переход к матрице нормированных значений;
- рассматривается симметричная матрица расстояний между элементами нормированной матрицы. Расстояние в n – мерном пространстве рассчитывается как модуль вектора евклидова (хеммингова) пространства, но каждая координата умножается на свой вес;
- поскольку матрица расстояний представляет собой симметричную матрицу, то для дальнейшего анализа выбирается ее верхняя (нижняя) половина. Элементы на главной диагонали исключаются из рассмотрения. Среди всех элементов рассматриваемой матрицы находится минимальный элемент. Строка найденного минимального элемента соответствует одному номеру наблюдений, а столбец другому. Эти два наблюдения объединяются в один кластер. Кластер в дальнейшем рассматривается как первый элемент исходной совокупности. При этом второй элемент исключается из дальнейшего рассмотрения. Количество элементов, вошедших в тот или иной кластер фиксируется. Таким образом размерность исходной информации уменьшается на единицу;
- вся процедура повторяется до тех пор, пока количество кластеров не станет равным заданному.
Пример
По данным, представленным в таблице 8.14, проведем классификацию n=5 цехов предприятий по двум показателям: расходы (млн.руб.) – x(1): и уровень прибыли x(2)
iii. Таблица 8.14.
Дата: 2019-02-02, просмотров: 364.