ЛЕКЦИЯ 14 ОБОБЩАЮЩАЯ КОМПЛЕКСНАЯ ОЦЕНКА

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ЛЕКЦИЯ 14 ОБОБЩАЮЩАЯ КОМПЛЕКСНАЯ ОЦЕНКА

ДЕЯТЕЛЬНОСТИ ПРЕДПРИЯТИЯ

Цели и задачи комплексного анализа экономического потенциала организации

Оценка производственного потенциала организации

Оценка финансового потенциала организации

Экономическая сущность хозяйственных резервов и их классификация

5. Методика определения величины резервов

Комплексный многомерный факторный анализ

Методы комплексной рейтинговой оценки

Показатели оценки производственной составляющей

Коэффициент обновления ОС 17,07 Коэффициент прироста ОС. 20,99 Коэффициент выбытия ОС 4,14

Показатели оценки материальной составляющей

Коэффициент неравномерности поставок материалов 1,56 Коэффициент вариации 2,4

Показатели оценки кадровой составляющей

Коэффициент оборота по приёму 20,9 Коэффициент оборота по выбытию 17,8 Коэффициент текучести кадров 17,4 Коэффициент постоянства кадров. 79,7

В вышеприведенной таблице полно представлены данные, характеризующие движение ППО в текущем периоде, и они позволяют сделать оценку его оставляющих. Значения показателей, характеризующих состояние составляющих ППО исследуемой организации, приведены в таблице 8.3.

Таблица 8.3

Текущее состояние составляющих ППО

Наименование показателя	Значение, %
Показатели оценки производственной составляющей
Коэффициент износа ОС	24,78
Коэффициент годности ОС	75,22
Коэффициенты использования парка: наличного, установленного, сданного в эксплуатацию оборудования	96,9 96,9 100
Показатели, характеризующие фонд времени использования оборудования, средний возраст машин и оборудования, лет	8,69
Коэффициенты использования производственных мощностей Коэффициент интегральной нагрузки	97,07
Показатели оценки материальной составляющей
Коэффициент обеспеченности материальными ресурсами фактический	105,23
Коэффициент обеспеченности материальными ресурсами плановый	97,61
Показатели оценки кадровой составляющей
Среднегодовая выработка товара одним работающим в предыдущем периоде, тыс.руб. в текущем периоде, тыс.руб.	531,72 647,49
Показатели баланса рабочего времени Удельный вес потерь рабочего времени Удельный вес простоев Удельный вес прогулов	63,40 9,48 59,85

Состав приведенных в таблице показателей и их значения отражают состояние составляющих ППО в текущем периоде.

В таблице 8.4 приведен набор показателей, характеризующих эффективность использования составляющих ППО исследуемой организации.

Таблица 8.4

Эффективность использования составляющих ППО

Наименование показателя

Значение, %

Показатели оценки производственной составляющей

Фондоотдача

4,34

Фондоемкость

23,0

Рентабельность по ОС

26,06

Коэффициент загрузки оборудования

91,07

Коэффициент сменности

Коэффициент интенсивной нагрузки оборудования

99,78

Показатель интегральной нагрузки.

96,85

Показатели оценки материальной составляющей

Материалоотдача товара

1,33

Материалоемкость товара

75,2

Удельный вес материальных затрат в себестоимости товара.

78,66

Оценка производственной составляющей

Износ основных средств

24,78 <50%

Соотношение коэффициентов обновления и выбытия основных средств.

17,07 >4,14

Фондоотдача

4,34> 1

Оценка материальной составляющей

1,2

Доля переменных затрат в себестоимости товара.

84,51>80 %

Соотношение изменения цен на сырье, материалы и изменения цен на товар.

< 1

Материалоотдача

1,33 < 1,5

Комплексная оценка ФПО.

На данном шаге определяется комплексная оценка ФПО.

Пример определения уровней ФПО приведен в таблице.

Таблица 8.10

Характеристика уровней финансового потенциала

Уровень ФПО	Краткая характеристика
Высокий уровень ФПО	Деятельность организации прибыльна. Финансовое положение стабильно.
Средний уровень ФПО	Деятельность организации прибыльна, однако финансовая стабильность во многом зависит от изменений, как во внутренней, так и во внешней среде.
Низкий уровень ФПО	Организация финансово нестабильна.

Данный этап рекомендуется проводить экспертным путем на основании значимости каждой составляющей.

Для нашего примера организация не по всем составляющим ФПО имеет высокие оценки, следовательно, ей можно присвоить средний уровень ФПО.

Таким образом, оценка производственного и финансового потенциала организации – необходимый этап стратегического анализа и управления, охватывающий все основные внутренние процессы. В результате такого анализа обеспечивается системный взгляд на организацию, который позволит не только выявить все сильные и слабые стороны, но и создать на этой основе комплексный план перспективного развития.

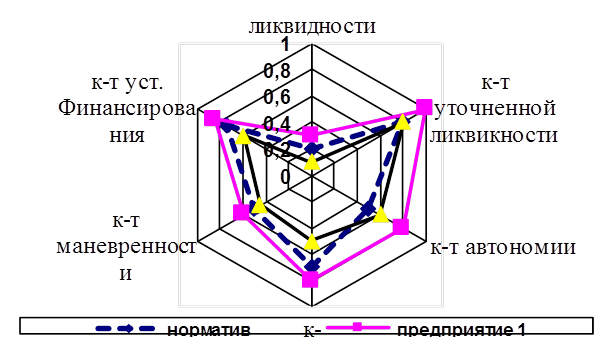
Пример 1

Имеются данные (табл.8.13.) по относительным показателям финансовой устойчивости и ликвидности предприятий. Изобразим их с помощью многоосевой диаграммы.

Таблица 8.13.

Показатели финансовой устойчивости и ликвидности предприятий

Показатели	Рекомендуемые нормативы	Предприятие 1	Предприятие 2
Коэффициент абсолютной ликвидности	0,2	0,3	0,1
Коэффициент уточненной ликвидности	0,8	1,0	0,8
Коэффициент автономии	0,5	0,8	0,6
Коэффициент обеспеченности запасов и затрат собственными источниками финансирования	0,7	0,8	0,5
Коэффициент маневренности	0,5	0,6	0,45
Коэффициент устойчивости финансирования	0,75	0,85	0,6

Рис. Пример многоосевой диаграммы

Кластерный анализ – один из методов многомерного анализа, предназначенный для группировки совокупности, элементы которой характеризуются многими признаками. Значения каждого из признаков служат координатами каждой единицы изучаемой совокупности в многомерном пространстве признаков. Каждое наблюдение, характеризующиеся значениями нескольких показателей, можно представить как точку в пространстве этих показателей, значения которых рассматриваются как координаты в многомерном пространстве.

Рассмотрим алгоритм кластерного анализа:

- от исходной совокупности наблюдений осуществляется переход к матрице нормированных значений;

- рассматривается симметричная матрица расстояний между элементами нормированной матрицы. Расстояние в n – мерном пространстве рассчитывается как модуль вектора евклидова (хеммингова) пространства, но каждая координата умножается на свой вес;

- поскольку матрица расстояний представляет собой симметричную матрицу, то для дальнейшего анализа выбирается ее верхняя (нижняя) половина. Элементы на главной диагонали исключаются из рассмотрения. Среди всех элементов рассматриваемой матрицы находится минимальный элемент. Строка найденного минимального элемента соответствует одному номеру наблюдений, а столбец другому. Эти два наблюдения объединяются в один кластер. Кластер в дальнейшем рассматривается как первый элемент исходной совокупности. При этом второй элемент исключается из дальнейшего рассмотрения. Количество элементов, вошедших в тот или иной кластер фиксируется. Таким образом размерность исходной информации уменьшается на единицу;

- вся процедура повторяется до тех пор, пока количество кластеров не станет равным заданному.

Пример

По данным, представленным в таблице 8.14, проведем классификацию n=5 цехов предприятий по двум показателям: расходы (млн.руб.) – x⁽¹⁾: и уровень прибыли x⁽²⁾

iii. Таблица 8.14.

Пример

Имеются данные показателей финансовой устойчивости по 10 предприятиям города. С помощью различных методов комплексной рейтинговой оценки составим их рейтинг.

1. Определим рейтинг с помощью метода геометрической средней

Для этого определим стандартизированные показатели, присвоив наилучшему значению показателя единицу. Лучшее значение коэффициента:

финансовой устойчивости 0,93

финансирования 14,27

инвестирования 1,32

маневренности 0,24

Покажем расчет рейтинга на примере предприятия №1

а₁= 0,42/0,93=0,451 b₁= 0,72/14,27=0,05

c₁= 1.21/1,32=0,916 d₁= 0,17/0,24=0,708

Таблица 8.15.

Расчет рейтинга по показателям финансовой устойчивости с помощью метода геометрической средней

Предприятия

Коэффициенты

Cтандартизированные показатели

Интегральный показатель

Рейтинг

финансовой устойчивости

финансирования

инвестирования

маневренности

0,42

0,72

1,21

0,17

0,451

0,050

0,916

0,708

0,350

0,6

1,53

1,23

0,19

0,645

0,107

0,931

0,791

0,475

0,81

4,31

1,21

0,17

0,871

0,302

0,916

0,708

0,643

0,44

0,8

1,32

0,24

0,473

0,056

1,000

0,405

0,7

2,34

1,25

0,2

0,752

0,164

0,946

0,833

0,560

0,93

14,27

1,32

0,24

1,000

0,89

8,36

1,21

0,17

0,957

0,585

0,916

0,708

0,776

0,78

3,61

1,29

0,22

0,838

0,253

0,977

0,916

0,660

0,75

3,04

1,26

0,21

0,806

0,213

0,954

0,875

0,616

10.

0,78

3,56

1,29

0,23

0,838

0,249

0,977

0,958

0,665

Далее согласно формулы находим произведение в степени ¼ стандартизированных показателей. Таким образом, рейтинг предприятия №1 равен:

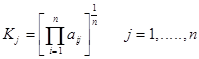
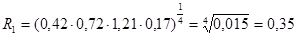
Среди исследуемых предприятий это наименьший результат, поэтому присваивается 10 место

2. Метод суммы мест предполагает предварительное ранжирование по выбранным показателям, затем суммирование и определение рейтинга.

iv. Таблица 8.16.

Расчет рейтинга с помощью метода суммы мест

Предприятия	Коэффициенты				Ранжирование показателей				Сумма мест
Предприятия	Фин. устойчивости	финансирования	инвестирования	маневренности	финансовой устойчивости	финансирования	инвест.	маневренности	Сумма мест
1.	0,42	0,72	1,21	0,17	10	10	8	8	36	10
2.	0,6	1,53	1,23	0,19	8	8	7	7	30	9
3.	0,81	4,31	1,21	0,17	3	3	1	8	15	2
4.	0,44	0,8	1,32	0,24	9	9	8	1	27	8
5.	0,7	2,34	1,25	0,2	7	7	6	6	26	7
6.	0,93	14,27	1,32	0,24	1	1	1	1	4	1
7.	0,89	8,36	1,21	0,17	2	2	8	8	20	2
8.	0,78	3,61	1,29	0,22	4	4	3	4	15	2
9.	0,75	3,04	1,26	0,21	6	6	5	5	22	6
10.	0,78	3,56	1,29	0,23	4	5	3	3	15	2

Покажем расчет рейтинга на примере предприятия №10

Сумма баллов по выбранным показателям составляет:

10+10+8+8=36

При использовании данного метода 1 место присваивается предприятию набравшему минимальную сумму мест. В нашем случае набранная сумма мест является максимальной, поэтому предприятие №1 в рейтинге занимает 10 место.

3. Определим рейтинг с помощью метода расстояний.

Стандартизированные показали нами были рассчитаны при определении рейтинга по средней геометрической, поэтому далее рейтинг для каждого предприятия определим по формуле:

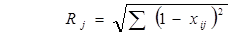
Таблица 8.17.

Расчет рейтинга с помощью метода расстояний

Предприятия	Коэффициенты				Cтандартизированные показатели				Интегральный показатель	Рейтинг
Предприятия	финансовой устойчивости	финансирования	инвестирования	маневренности	а	b	c	d	Интегральный показатель	Рейтинг
1.	0,42	0,72	1,21	0,17	0,451	0,050	0,916	0,708	1,138	10
2.	0,6	1,53	1,23	0,19	0,645	0,107	0,931	0,791	0,985	8
3.	0,81	4,31	1,21	0,17	0,871	0,302	0,916	0,708	0,772	5
4.	0,44	0,8	1,32	0,24	0,473	0,056	1,000	1,000	1,081	9
5.	0,7	2,34	1,25	0,2	0,752	0,164	0,946	0,833	0,889	7
6.	0,93	14,27	1,32	0,24	1,000	1,000	1,000	1,000	0,000	1
7.	0,89	8,36	1,21	0,17	0,957	0,585	0,916	0,708	0,515	2
8.	0,78	3,61	1,29	0,22	0,838	0,253	0,977	0,916	0,770	4
9.	0,75	3,04	1,26	0,21	0,806	0,213	0,954	0,875	0,821	6
10.	0,78	3,56	1,29	0,23	0,838	0,249	0,977	0,958	0,769	3

Так для предприятия №1 рейтинг составит:

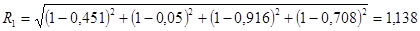
Максимальное значение интегрального показателя свидетельствует о последнем месте в рейтинге среди исследуемых предприятий по выбранным показателям.

Подведем итоги и составим таблицу расчета рейтинга предприятий по показателям финансовой устойчивости, с помощью различных методов комплексной оценки.

Данные таблицы 8.18. показывают, что все способы дали один и тот же вариант распределения рейтинга среди 10 предприятий города.

v. Таблица 8.18.

Итоги расчета рейтинга по показателям финансовой устойчивости с помощью методов комплексной оценки

Предприятия	Коэффициенты				МЕСТО В РЕЙТИНГЕ
Предприятия	финансовой устойчивости	финансирования	инвестирования	маневренности	Метод суммирования	Метод геометрической средней	Метод расстояний
1.	0,42	0,72	1,21	0,17	10	10	10
2.	0,6	1,53	1,23	0,19	8	8	8
3.	0,81	4,31	1,21	0,17	5	5	5
4.	0,44	0,8	1,32	0,24	9	9	9
5.	0,7	2,34	1,25	0,2	7	7	7
6.	0,93	14,27	1,32	0,24	1	1	1
7.	0,89	8,36	1,21	0,17	2	2	2
8.	0,78	3,61	1,29	0,22	4	4	4
9.	0,75	3,04	1,26	0,21	6	6	6
10.	0,78	3,56	1,29	0,23	3	3	3

ЛЕКЦИЯ 14 ОБОБЩАЮЩАЯ КОМПЛЕКСНАЯ ОЦЕНКА

ДЕЯТЕЛЬНОСТИ ПРЕДПРИЯТИЯ

Дата: 2019-02-02, просмотров: 709.

12 3 4 5 6 7 8 9 Следующая ⇒