Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

3.3.1. Расчётное контактное напряжение для цилиндрических передач /2,с.31/

 

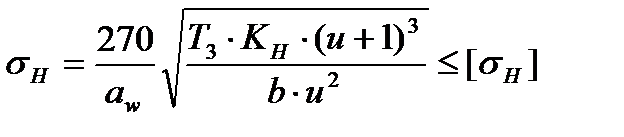                     ,                        (3.11)   

где K_H  – коэффициент нагрузки;

b    – ширина колеса расчётная (наименьшая).

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

13

ДМ 82 00 00 00

Окружная скорость колёс

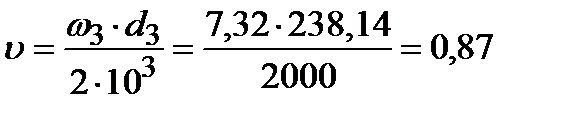м/с

  При такой скорости назначаем восьмую степень точности /2,с.32/.

Коэффициент нагрузки при проверочном расчёте на контактную прочность

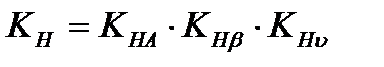                                                                      (3.12)

 

  где 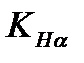  – коэффициент, учитывающий неравномерность распределения               нагрузки между зубьями;

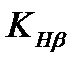  – коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба; 

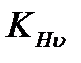  – коэффициент, учитывающий дополнительные динамические нагрузки.

По рекомендациям /2, с.39,40/ назначаем следующие значения коэффициентов:

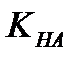 – = 1,07 при окружной скорости 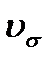=0,87 м/с и восьмой степени точности;

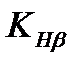– = 1,06 при значении коэффициента 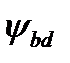=1,05, твёрдости зубьев менее НВ 350 и симметричном расположении относительно опор;

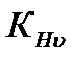 – = 1 при окружной скорости 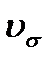=0,87 м/с , восьмой степени точности и твердости менее НВ 350.

 

   Расчет по формуле (3.12) дает .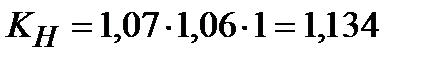

Ширину колеса берем в расчет минимальную и суммарную для обоих колес, т.е. в=80. Момент на колесе Т₃=482,24 Н∙м.

    Расчет по формуле (3.11) дает

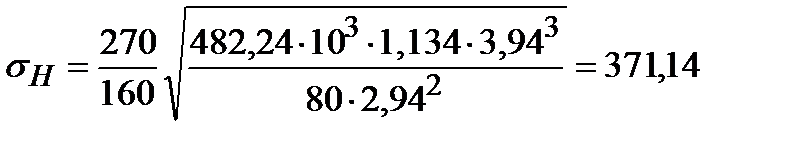                                                                                                                                                                              МПа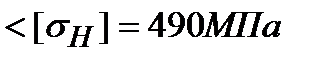           

                                           

 Условие прочности выполняется.

 

3.3.1 Расчет зубьев на контактную прочность по формуле (3.11) при кратковременных перегрузках моментом 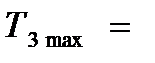1007,88 Н×м  дает        

Изм.

Лист

№ докум.

Подпись

Дата

Лист

14

ДМ 82 00 00 00

        

 

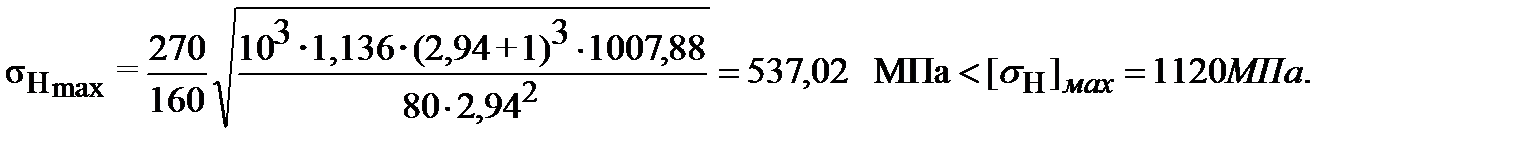
3.3.3 Напряжение изгиба зубьев  цилиндрических колёс при проверочном расчёте на выносливость вычисляются по формуле /2,с.46/

 

 

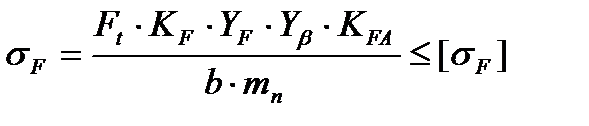                                             (3.13)

где F_t – окружная сила;

     K_F   – коэффициент нагрузки;

     Y_F  – коэффициент формы зуба;

     Y_β  – коэффициент, компенсирующий погрешности, возникающие из-за

              применения для косых зубьев той же расчётной схемы, что и для

              прямых;

     K_FA –  коэффициент, учитывающий неравномерность распределения на    

              грузки между зубьями;

     b – ширина колеса, находящаяся в зацеплении, мм;

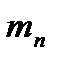     – модуль нормальный, мм;

В зацеплении колёс быстроходной передачи действуют следующие силы:

– окружная 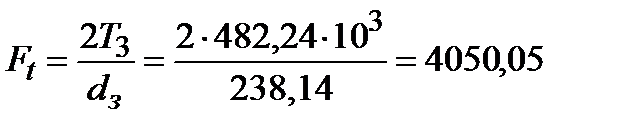              H;

 

     – радиальная 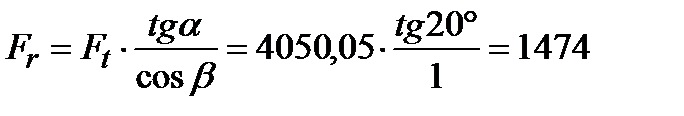       Н;

 

Коэффициент нагрузки /2, с.42/

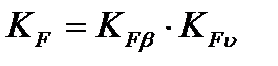                                                         (3.14)

где 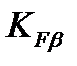– коэффициент, учитывающий неравномерность распределения          нагрузки по длине зубьев;       

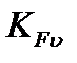– коэффициент, учитывающий дополнительные динамические   нагрузки.

 

Примем /2,с.43/ 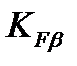=1,11с учетом, что твердость колес менее НВ 350, коэффициент  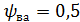,а каждое из колес расположено симметрично относительно опор.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

15

ДМ 82 00 00 00

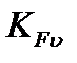Назначим =1,25, учитывая дополнительно, что окружная скорость 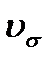=0,87 м/с, а степень точности принята 8.

Тогда по формуле (3.14) 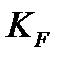=1,11·1,25=1,388

Без расчётов, руководствуясь только рекомендацией /2,с.47/, возьмём К_FA=0,92.

Коэффициент Y_β определим по формуле /2, с.46/:

                   

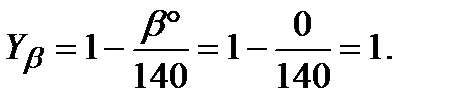
Коэффициент формы зуба 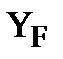, для прямозубых колес зависит от эквивалентного числа зубьев /2,с.46/,которое составляет

 для шестерни и колеса соответственно

 

       

 

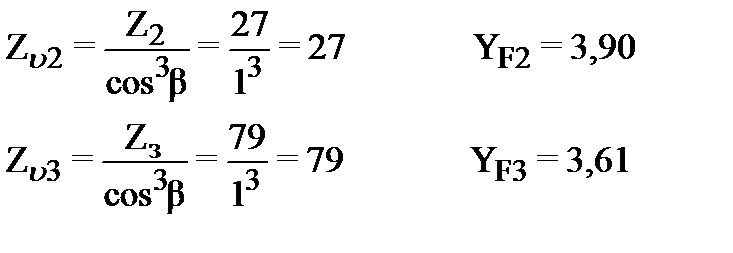
Расчет по формуле (3.13) дает для шестерни и колеса соответственно   (в МПа):

       

                    

Это значительно меньше вычисленных в пункте 3.1.4 допускаемых напряжений 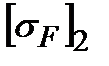=237 МПа и 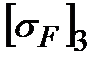=206 МПа.

 

3.3.4 Напряжение изгиба при кратковременных перегрузках вычисляются также по формуле (3.13) куда вместо окружной силы F_t следует подставить окружную силу при кратковременных перегрузках

                  

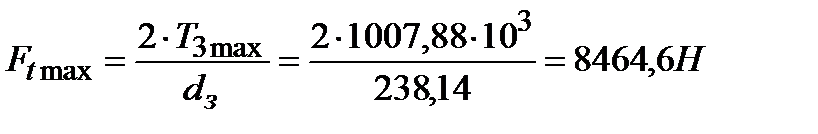
После подстановки получаем при перегрузках соответственно для шестерни и колеса напряжение изгиба

 

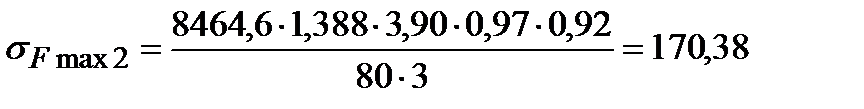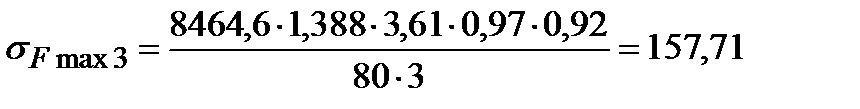МПа

 

              МПа

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

16

ДМ 82 00 00 00

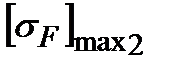Эти напряжения значительно меньше вычисленных в пункте 3.1.5 допускаемых напряжений =352 МПа и 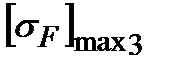=320 МПа.

 

3.3.5 Геометрические параметры колес цилиндрической передачи, обоснованные в результате расчетов, сведены в таблицу 3.1.

 

 

Таблица 3.1 – Геометрические параметры колес зубчатой передачи

Параметры

Шестерня

Колесо

Межосевое расстояние, мм

160

160

Нормальный модуль, мм

3

3

Угол наклона зубьев, град

0

0

Число зубьев

27

79

Направление зубьев

-

-

Делительные диаметры, мм

81

238,14

Диаметры вершин зубьев, мм

87

244,14

Диаметры впадин зубьев, мм

73,5

230,64

Ширина венцов колёс, мм

85

80

 

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

17

ДМ 82 00 00 00

4. Расчет ременной передачи

Исходные данные для расчета

– передаваемая мощность P₁=3,83кВт;

– частота вращения ведущего шкива n₁ = n_дв =720 об/мин ;

– передаточное отношение 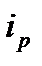= 3,5;

– момент на ведущем шкиве T₁=50,82 Н·м ;

– относительное скольжение ремня 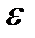 =0,015 возьмем по рекомендации /3,с.131/