Для непрерывной случайной величины невозможно описать закон распределения с помощью таблицы, в которой были бы перечислены все возможные значения этой величины и их вероятности. Однако различные области возможных значений этой величины все же не являются одинакого вероятными. т.е. и для непрерывной случайной величины существует свое “распределение вероятностей”, хотя и не в том смысле, как для дискретной величины.
1. Функцией распределения непрерывной случайной величины Х называется функция F(x) равная вероятности того, что случайная величина приняла значение, меньшее х: F ( x ) = P ( X < x ) .
Функцию F(x) называют еще интегральной функцией распределения.
Геометрически это равенство можно истолковать так: функция F(x) есть вероятность того, что случайная величина Х (случайная точка Х на оси Ох ) в результате опыта попадет левее точки х (рис. 3.).
Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения. Причем она существует для всех случайных величин, как дискретных, так и непрерывных.
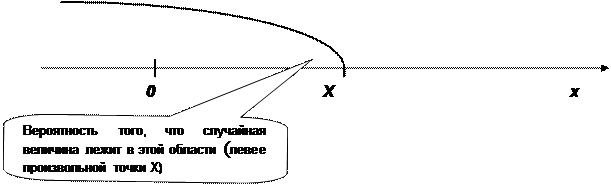 |
Рис. 3. Геометрический смысл функции распределения непрерывной случайной величины.
2. Основные свойства функции распределения:
1) Функция распределения принимает значения в интервале (0; 1):
0 ≤ F(х) ≤ 1.
2) F(x) - неубывающая функция, т.е. если х2 > х1 , то и F (х2 ) > F (х1).
3) Если все возможные значения непрерывной случайной величины X принадлежит интервалу ( a ; b ), то:
F ( x ) = 0 при x ≤ a; F ( x ) =1 при x ≥ b.
Следствие. Если возможные  значения непрерывной случайной велечины расположены на всей числовой оси, то справедливы следующие предельные соотношения :
значения непрерывной случайной велечины расположены на всей числовой оси, то справедливы следующие предельные соотношения :


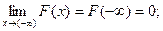

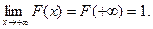
Это значит, что график функции распределения расположен в полосе, ограниченной прямыми y=0 и y =1.
3. Функцию f ( x ), равную производной ее интегральной функции распределения F ( x ) называемой плотностью распределения (или плотностью вероятности) непрерывной случайной велечины X: f ( x )= F / ( x ).
Поэтому функцию f ( x ) называют дифференциальной функцией распределения .
4. Кривая у= f ( x ), изображающая плотность распределения случайной величины называемой кривой распределения.
5. Основные свойства функции распределения:
1) Функция f ( x ) является неотрицательной: 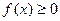
2) Вероятность того, что непрерывная случайная величина в результате испытания примет какое-либо значение из интервала (а,в) равна определенному интегралу от плотности вероятности в пределах от а до в :
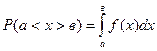 ; так как f ( x )= F / ( x ),
; так как f ( x )= F / ( x ),
то 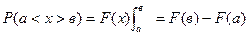
Т.о. вероятность того, что случайная величина примет значение, заключенное в интервал (а; в), равна приращению функции распределения на этом интервале F (в) - F (а).
Геометрически это выражение можно обосновать так (рис. 4.): вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (а; в) численно равна площади криволинейной трапеции, ограниченной осью Ох, прямыми х=а, х=в и кривой f ( x ).
Следствие 1 . Заменив пределы интегрирования а на 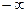 , в на х получим интеграл с переменным верхним пределом, который равен функции распределения этой случайной величины.
, в на х получим интеграл с переменным верхним пределом, который равен функции распределения этой случайной величины. 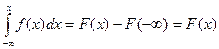
Следствие 2 . Несобственный интеграл от функции плотности распределения равен 1.
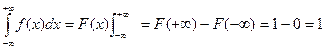 .
.
Это равенство называют условием нормировки плотности вероятности.
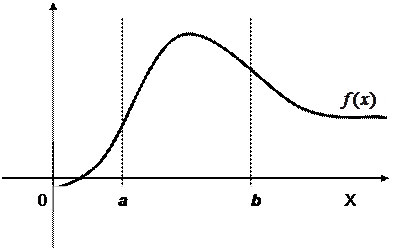
Рис. 4. Геометрический смысл функции плотности вероятности непрерывной случайной величины.
6. Числовые характеристики непрерывной случайной величины X с плотностью распределения f( x ) определяющая аналогично числовым характеристикам дисперсных случайных величин (за исключением моды и медианы).
· Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку (а;в) называют величину определенного интеграла:
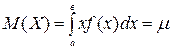 , где f ( x ) - плотность вероятности.
, где f ( x ) - плотность вероятности.
Название математического ожидания – центр распределения вероятностей случайной величины Х для непрерывных случайных величин даже более актуально, чем для дискретных.
· Дисперсией непрерывной случайной величины Х, возможные значения которой принадлежат отрезку (а; в), называют величину определенного интеграла:
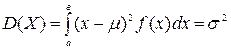 ,
,
где 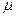 - математическое ожидание ; f ( x ) - плотность вероятности.
- математическое ожидание ; f ( x ) - плотность вероятности.
· Среднее квадратичное отклонение нерперывной случайной величины 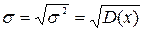 .
.
Пример 15.
Непрерывная случайная величина задана функцией распределения
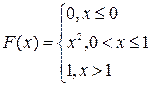
Найти М(Х), D(X), σ.
Решение.
1) Найдем функцию плотности вероятности 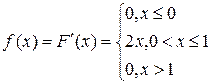
2) 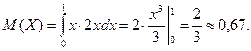
3) 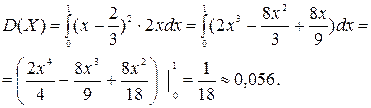
4) 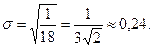
Дата: 2019-02-02, просмотров: 382.