Кафедра физики и медицинской информатики
ОСНОВЫ
ТЕОРИИ ВЕРОЯТНОСТЕЙ
Методическое пособие для студентов - заочников
Великое множество событий совершается в окружающем нас мире. События взаимосвязаны – одни из них являются следствием (исходом) других и, в свою очередь, служат причиной третьих. Вглядываясь в гигантский водоворот взаимосвязанных явлений, можно сделать два важных вывода. Во-первых, наряду с совершенно определенными, однозначными исходами встречаются неоднозначные. Если первые можно предсказать точно, то вторые допускают лишь вероятные предсказания. Во-вторых, неоднозначные исходы встречаются чаще чем однозначные.
Вы нажимаете кнопку настольной лампы, и она зажигается. Здесь второе событие (загорелась лампа) является однозначным исходом первого события (нажата кнопка). Такое событие называется строго детерминированным. Другой пример: вы подбрасываете игральный кубик, на разных гранях которого изображены различные числа; и кубик падает так, что на верхней грани оказывается 4 очка. В данном случае второе событие (выпала четверка) уже не является однозначным исходом первого события (подброшен кубик). Ведь могло выпасть любое число от 1 до 6. Выпадение того или иного числа очков есть пример случайного события. Из приведенных примеров хорошо видно различие между строго детерминированными и случайными событиями.
Со случайными событиями (и вообще со случайностями разного рода) мы встречаемся очень часто, значительно чаще, чем это обычно принято считать. Случаен результат встречи двух спортивных команд одного и того же уровня подготовки, количество солнечных дней в данной местности изменяется от года к году случайным образом .
Совокупность случайных факторов лежит в основе любого процесса массового обслуживания – торговли, телефонной связи, транспорта, медицинской помощи и т . д .
Часть I . ВЕРОЯТНОСТЬ СЛУЧАЙНЫХ СОБЫТИЙ
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
1.Испытанием или опытом в теории вероятностей называется любая совокупность условий, которая может без изменения повторяться сколько угодно большое число раз.
2.Результат испытания называется исходом.
3.Исход, интересующий нас в данном испытании называется событием.
Для обозначения событий используют заглавные (прописные) буквы латинского, реже русского, алфавита.
Пример 1:
Испытание: бросание игральной кости (кубика с пронумерованными от 1 до 6 очков гранями).
Всевозможные исходы этого испытания:
· Появление 1 очка на верхней грани;
· Появление 2 очков на верхней грани;
· Появление 3 очков на верхней грани;
· Появление 4 очков на верхней грани;
· Появление 5 очков на верхней грани;
· Появление 6 очков на верхней грани.
Событие А1 - появление 1 очка на верхней грани;
Событие А2 - появление 2 очков на верхней грани;
Событие А3 - появление 3 очков на верхней грани;
Событие А4 - появление 4 очков на верхней грани;
Событие А5 - появление 5 очков на верхней грани;
Событие А6 - появление 6 очков на верхней грани;
Событие В - появление четного числа очков на верхней грани;
Событие С - появление нечетного числа очков на верхней грани;
Событие D - появление 4 очков на верхней грани и т.п.
4. Классическое определение вероятности.
Вероятностью события называется отношение числа исходов, в которых может появиться данное событие (благоприятных для появления события), к общему числу всевозможных исходов испытания.
Вероятность события обозначается прописной латинской буквой Р с указанием в скобках обозначения события, например: вероятность события А – Р(А), число всевозможных исходов испытания обозначается буквой n, а число благоприятных исходов – буквой m или, конкретизируя какому именно событию благоприятствуют данные исходы, - mА, значение (величина) вероятности обозначается строчной латинской буквой p.
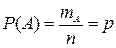 ,
, 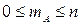
Пример 2:
· При бросании кубика (смотри пример 1) появлению события А будет благоприятствовать один исход (m=1) из 6 возможных (n=6), значит вероятность этого события будет равна 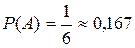 ;
;
· Появлению события В будут благоприятствовать 3 исхода (m=3) из 6 возможных, т.е. благоприятными будут исходы с появлением четных цифр 2, 4, 6, значит вероятность появления этого события 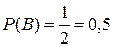
5. Событие называется случайным, если оно может появиться или не появиться в результате данного испытания. Если событие обязательно происходит в каждом исходе данного испытания, оно называется достоверным событием, если же событие не может произойти ни при одном исходе – оно называется невозможным.
6. Событие называется противоположным данному событию, если в результате испытания могут произойти только эти два события и они не могут появиться одновременно. Событие, противоположное данному событию А обозначается той же самой буквой, но с чертой над ней: 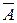 , значение вероятности противоположного события
, значение вероятности противоположного события 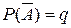 .
.
Пример 3:
При бросании монеты возможны два события:
· Событие А – появление «орла»;
· Событие В – появление «решки» или, иначе, не появление «орла».
Значит событие В можно считать противоположным событию А, т.е. 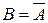 .
.
7. Основные свойства вероятности:
· Вероятность случайного события является неотрицательным числом и не превышает единицы: 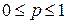 , т.к.
, т.к. 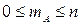 .
.
· Вероятность достоверного события равна единице: 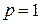 , т.к.
, т.к. 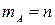 .
.
· Вероятность невозможного события равна нулю: 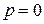 , т.к.
, т.к. 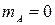 .
.
· Сумма вероятностей данного и противоположного событий равна единице: 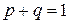 .
.
8. Два события называются равновозможными, если в результате опыта вероятности их появления равны.
9.Случайные события образуют полную группу, если при каждом испытании может осуществиться любое из них и не может осуществиться событие несовместимое с ним.
События, образующие полную группу иногда называют элементарными событиями.
Пример 4.
· Выпадение ‘орла’ или ‘решки’ при бросании монеты один раз.
· Выпадение 1,2,3,4,5 или 6 очков при бросании кубика один раз.
10. Два события называются совместными, если в результате опыта появление одного из них не противоречит появлению другого, т.е. они могут появиться одновременно. События, которые не могут ни при каких условиях появиться одновременно, т.е. появление одного из событий исключает появление другого, называются несовместными.
11. Два события называются зависимыми если вероятность появления одного из них зависит от того, произошло предварительно другое событие или нет, в противном случае, т.е. когда вероятность появления одного события не зависит от наступления другого, события называются независимыми.
Вероятность наступления события А, которое зависит от события В, называется условной вероятностью и обозначается 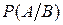 .
.
12. Суммой двух событий (А + В) называется событие С, которое заключается в наступлении по крайней мере (хотя бы) одного из этих событий, т.е. или первого, или второго, или обоих событий одновременно С = А + В = А или В.
13. Произведением двух событий (А * В) называется событие Д, которое заключается в одновременном наступлении обоих событий, т.е. и первого, и второго.
ФОРМУЛА БЕРНУЛЛИ
1. При практическом использовании теории вероятностей особое значение имеют события, связанные с независимыми повторными испытаниями, для которых выполняются условия:
| Эти условия получили название "схемы Бернулли" | 1) число испытаний n конечно;
2) каждое испытание имеет только два исхода:
· событие А осуществилось;
· событие А не осуществилось;
3) все испытания независимые;
4) вероятность появления события А в каждом испытании постоянна 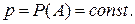
|
Пример 7.
1. При подбрасывании монеты выпадение "орла" и "решки" удовлетворяют этим условиям.
2. Многолетние наблюдения показывают, что в течении дня соль приобретают 10% покупателей бакалейного отдела. Какова вероятность, что из 100 покупателей, приобретающих товар в бакалейном отделе равно 10 будут покупать соль?
То есть во многих задачах требуется найти не вероятность каждого отдельного события, а вероятность осуществления события А ровно m раз в данной серии из n испытаний. Для этого пользуются формулой Бернулли.
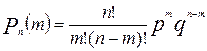
Здесь:
р - вероятность появления события А в отдельном испытании;
q - вероятность противоположного события q=1- p;
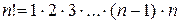 (читается «эн факториал» - произведение последовательных натуральных чисел от 1 до n, например 5!=1×2×3×4×5=120).
(читается «эн факториал» - произведение последовательных натуральных чисел от 1 до n, например 5!=1×2×3×4×5=120).
Пример 8.
Вернемся к предыдущему примеру с покупателями соли.
Вероятность покупки соли отдельным покупателем р=0,1, значит вероятность противоположного события, т.е. того, что соль не будет куплена q =1- p =1-0,1=0,9.
Общее число покупателей n=100, число предполагаемых покупателей соли m=10, поэтому n- m=100-10=90.
Подставляем данные в формулу Бернулли:
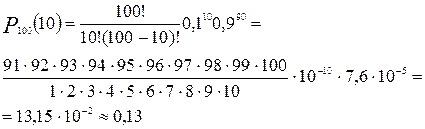
Вероятность того, что из данных 100 покупателей соль приобретут ровно 10 человек равна 13%, хотя по статистике только каждый 10-ый покупатель приобретает в этом отделе соль.
2. Частные случаи формулы Бернулли:
1. Вероятность осуществления события n раз в n испытаниях
(m = n): 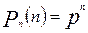 .
.
2. Вероятность осуществления события А ноль раз в n испытаниях (m = 0): 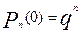 .
.
3. Вероятность осуществления события А не более m раз в n испытаниях: 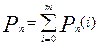 .
.
4. Вероятность осуществления события А не менее m раз из n испытаний: 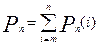 .
.
Пример 9.
Найти вероятность того, что в семье, имеющей пять детей, будет:
1) две девочки; 2) не менее двух девочек;
3) не более 4х девочек.
Считать вероятность рождения мальчика p м = 0,4 и девочки pд= 0,6.
Решение.
Общее количество детей n=5, вероятность рождения девочки p=0,6, значит вероятность рождения мальчика, т.е. не девочки q=1-0,6=0,4;
1) m=2. 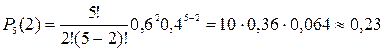
2) m³2.
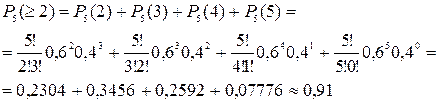
3) m£4.
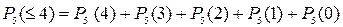
или, что тоже самое
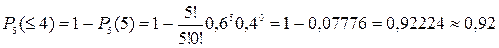

3. При большом числе n повторных испытаний некоторого события А формулой Бернулли пользоваться сложно. В этом случае используют формулу Лапласа.
Если вероятность осуществления события А в n испытаниях отличны от 0 и 1, то вероятность, что это событие осуществиться равно m раз равна значению функции:
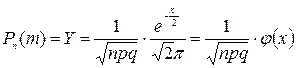 ,
,
где  - функция Лапласа, причем
- функция Лапласа, причем 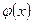 - функция четная и для определения ее значений есть таблица (табл. 1.);
- функция четная и для определения ее значений есть таблица (табл. 1.);
аргумент функции 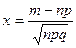 .
.
Пример 10.
Вероятность заболевания туберкулезом легких в некоторой местности 0,003. Какова вероятность того, что при осмотре 1000 человек будет выявлено 3 больных?
 n=1000 Р1000(3) =
n=1000 Р1000(3) = 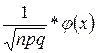 , где
, где 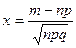
m=3 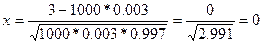 ,
, 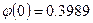
p=0,003
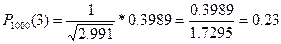 .
.
4. Формула Лапласа непригодна при малых значениях вероятности события А в одиночных испытаниях , (т.е. при р 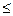 0.1). В этом случае пользуются законом редких событий (законом Пуассона):
0.1). В этом случае пользуются законом редких событий (законом Пуассона):
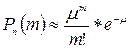 ,
,
где 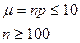
Пример 11.
Фармацевтический завод отправил на аптечный склад 10 000 ампул димедрола. Вероятность того, что в пути ампула будет повреждена 0.0002. Найти вероятность того, что на склад поступить 5 ампул поврежденных из этой серии.


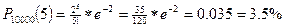
6. Наивероятнейшим числом появления события называется такое число повторений события, вероятность которого наибольшая.
По определению наивероятнейшее число появлений события К0 должно удовлетворять двум неравенствам:
Р n ( K 0 ) 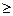 Pn ( K 0 +1)
Pn ( K 0 +1)
Pn ( K 0 ) 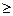 Pn ( K 0 -1)
Pn ( K 0 -1)
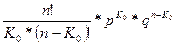
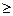
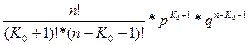

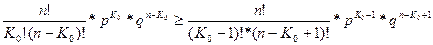
Решая эти неравенства, получаем:
K0 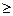 np - q
np - q
K 0 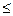 np + p
np + p
или двойное нерaвенство: ( np – q ) 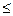 K 0
K 0 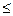 ( np + p )
( np + p )
Равенство имеет место, если ( np - q ) – целое число; тогда в этом случае К0 имеет два значения: K 0 =( np - q ) и K 0 = ( np + p ).
Если же ( np - q ) – дробное число, то между числами ( np - q ) и ( np + p ) заключено единственное целое число К0.
Если ( np )- целое число, то К0= np.
Примеры 12.
1. Вероятность производства нестандартной детали р=0,022. Найти наивероятнейшее число нестандартных деталей в партии на 500 деталей.
N=500 n*p-q=500*0.022-0,978=11-0,978=10,022
P=0.022 n*p+p=500*0.022+0.022=11.022
Q=0.978 10.022 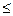 K0
K0 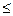 11.022 K 0 =11
11.022 K 0 =11
2. Вероятность попадания в цель при одном выстреле из орудия равна 0,2. Найти наивероятнейшее число попаданий в цель, если будет сделано 14 выстрелов.
N=14 n*p-q=14*0.2-0.8=2.8-0.8=2.0
P=0.2 n*p+p=14*0.2+0.2=2.8+0.2=3.0
Q=0.8 K 0 =2; K 0 =3
3. Найти наивероятнейшее число выпадения герба при 100 подбрасываниях монеты.
N=100 n*p=100*0.5=50 n*p-q=50-0.5=49.5
P=0.5 K0=50 n*p+q=50+0.5=50.5



 Q=0.5 49.5
Q=0.5 49.5 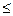 K0
K0 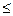 50.5
50.5
K 0 =50
Кафедра физики и медицинской информатики
ОСНОВЫ
ТЕОРИИ ВЕРОЯТНОСТЕЙ
Методическое пособие для студентов - заочников
Великое множество событий совершается в окружающем нас мире. События взаимосвязаны – одни из них являются следствием (исходом) других и, в свою очередь, служат причиной третьих. Вглядываясь в гигантский водоворот взаимосвязанных явлений, можно сделать два важных вывода. Во-первых, наряду с совершенно определенными, однозначными исходами встречаются неоднозначные. Если первые можно предсказать точно, то вторые допускают лишь вероятные предсказания. Во-вторых, неоднозначные исходы встречаются чаще чем однозначные.
Вы нажимаете кнопку настольной лампы, и она зажигается. Здесь второе событие (загорелась лампа) является однозначным исходом первого события (нажата кнопка). Такое событие называется строго детерминированным. Другой пример: вы подбрасываете игральный кубик, на разных гранях которого изображены различные числа; и кубик падает так, что на верхней грани оказывается 4 очка. В данном случае второе событие (выпала четверка) уже не является однозначным исходом первого события (подброшен кубик). Ведь могло выпасть любое число от 1 до 6. Выпадение того или иного числа очков есть пример случайного события. Из приведенных примеров хорошо видно различие между строго детерминированными и случайными событиями.
Со случайными событиями (и вообще со случайностями разного рода) мы встречаемся очень часто, значительно чаще, чем это обычно принято считать. Случаен результат встречи двух спортивных команд одного и того же уровня подготовки, количество солнечных дней в данной местности изменяется от года к году случайным образом .
Совокупность случайных факторов лежит в основе любого процесса массового обслуживания – торговли, телефонной связи, транспорта, медицинской помощи и т . д .
Дата: 2019-02-02, просмотров: 376.