Закон распределения случайной величины не всегда бывает известен. В этом случае для описания случайной величины достаточно бывает указать её числовые характеристики, которые выражают наиболее существенные особенности распределения.
К числовым характеристикам относятся: математическое ожидание, мода, медиана, дисперсия, среднее квадратическое отклонение.
1. Математическим ожиданием дискретной случайной величины X называют сумму произведений всех возможных значений случайной величины Х на вероятность этих значений:
.
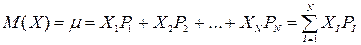Математическое ожидание - центр распределения и его можно рассматривать как "истинное'' значение случайной величины.
При большом числе испытаний n среднее арифметическое значение случайной величины близко к ее математическому ожиданию.
Пусть Х принимает значение x 1 m 1 раз, значение x 1 - m 1 раз, и т.д.; причем m 1 + m 2 +... mn = n, тогда:
.
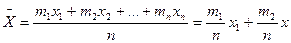
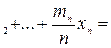
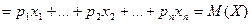При большом числе испытаний n их относительная частота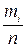 
стремится к вероятности p 1 (статистическое определение вероятности).
2. Основные свойства математического ожидания:
1) Математическое ожидание постоянной величины равно этой постоянной:
M(C) = C.
2) Постоянный множитель можно выносить за знак математического ожидания:
M(CX) = С*M(X), где с = const .
3) Mатематическое ожидание суммы случайных величин X и Y равно сумме их математических ожиданий:
.
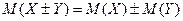4) Mатематическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
M ( X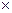 
Y ) =M ( X ) 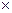M( Y ).
3. Модой М0 дискретного распределения случайной величины называют такое значение случайной величины, которому соответствует наибольшая вероятность.
4. Медианой Ме дискретного распределения случайной величины называют серединное значение между наименьшим и наибольшим значениями случайной величины.
Кроме математического ожидания мода и медиана являются характеристиками положения случайной величины.
5. Часто бывает необходимо знать степень рассеяния (разброса) случайной величины около математического ожидания. Для этого используют понятие дисперсии дискретной случайной величины.
Дисперсия D ( X ) равна математическому ожиданию квадрата разности случайной величины и ее математического ожидания :
,
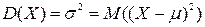где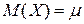 
- математическое ожидание случайной величины, и величина 
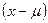- это центрированная случайная величина или отклонение.
Учитывая определение математического ожидания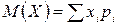 
, можно записать для дисперсии:
.
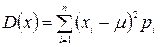Иначе дисперсия равна разности математического ожидания квадрата случайной величины и квадрата математического ожидания случайной величины:
.
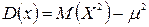Эти формулы можно применять для вычисления дисперсии равнозначно, т.к.
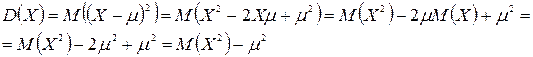
6. Свойства дисперсии случайной величины:
1) Дисперсия постоянной величины равна нулю, т.е. постоянная величина дисперсии не имеет:
D(С) = 0.
2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
D(С*X) =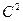 
*D(X).
3) Дисперсия суммы или разности двух независимых случайных величин равна сумме дисперсий этих величин :
D (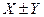 
)= D ( 
) 
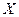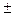D ( 
).
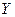7. Дисперсия имеет размерность квадрата случайной величины. В тех случаях, когда нужно иметь числовую характеристику рассеяния возможных значений в той же размерности, что и сама случайная величина, используют среднее квадратичное значение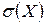 
: 
.
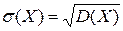Пример 14. Пусть закон распределения случайной величины задан следующей таблицей:
| X | 1 | 2 | 4 | 5 |
| P | 0.5 | 0.4 | 0.3 | 0.1 |
1) М0 = 2, т.к. вероятность для этого значения случайной величины наибольшая (p2 = 0,4).
2) Ме = 3 – это середина отрезка (1; 5).
3) M(Х)=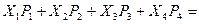 
.
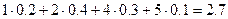4) 
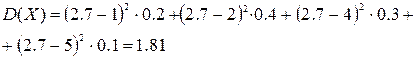или
5) D(x)=M(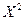 
) - 
= 
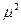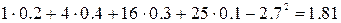
6) 
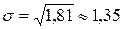М ± s = 2,7 ± 1,35
 |
Рис.2. Расположение числовых характеристик на числовой прямой.
Дата: 2019-02-02, просмотров: 258.
