Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Задача № 6  

Имеются 4 урны с шарами. В первых трех по 1 белому и 1 черному, в четвертой - 4 белых и 1 черный.

1. Из наугад взятой урны достали шар. Найти вероятность того, что он белый.

2. Наугад вынутый шар оказался белым. Найти вероятность того, что он из четвертой урны.

Решение.  

1. Пусть событие А состоит в том, что вынутый шар – белый. Это событие наступает в результате появления одного из двух несовместных событий (гипотез): В₁ – выбрали одну из первых трех урн;

В₂ – выбрали четвертую урну.

Очевидно, вероятности гипотез равны Р(В₁)= 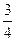, Р(В₂)= .

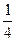Тогда, по формуле полной вероятности

.

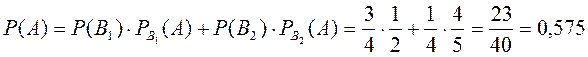Здесь 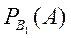 - вероятность извлечь белый шар из урны с одним белым, одним черным шарами,  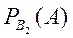- вероятность извлечь белый шар из четвертой урны.

Очевидно = , = .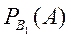

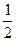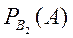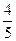2. Событие А уже произошло (вынули белый шар). Нужно найти так называемую переоцененную вероятность гипотезы В₂ - 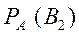. Применяем формулу Байеса

.

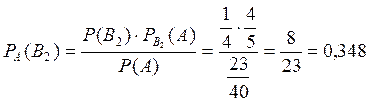Замечание: при сравнении переоцененной вероятности с безусловной убеждаемся, что они различны.

Ответ:

1. Вероятность того, что из наугад взятой урны достали белый шар, равна 0,575.

2. Вероятность того, что белый шар оказался из четвертой урны, равна 0,348.

 

Распределение Пуассона

Задача №7

Корректура в 400 страниц содержит 800 опечаток. Найти вероятность того, что наугад взятая страница содержит 3 опечатки.

Решение.  

Находим среднее число опечаток на одной странице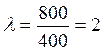

Применяем формулу Пуассона 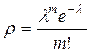 для 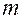=3. Получаем, что искомая вероятность равна .

 

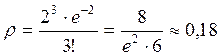Локальная, интегральная теоремы Лапласа, теорема Бернулли.

Задача №8

Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.

Решение.

По условию, n=243; k=70; p=0,25; q=0,75. Так как n=243 – достаточно большое число, воспользуемся локальной теоремой Лапласа:

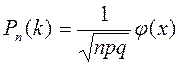, где  .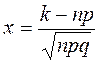

Найдем значение x:

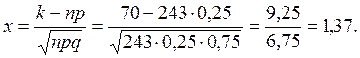
По таблице значений функции   

                           

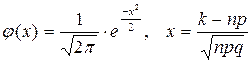
 найдем .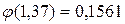

 Искомая вероятность

                       

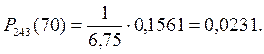
Ответ: вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, равна 0,0231.

Задача №9

Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна p=0,8. Найти вероятность того, что событие появится: а) не менее 75 раз и не более 90 раз; б) не менее 75 раз; в) не более 74 раз.

Решение.

Воспользуемся интегральной теоремой Лапласа:

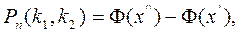 где Ф(x) – функция Лапласа,

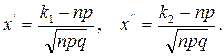
а) по условию, n=100; p=0,8; q=0,2; k₁=75; k₂=90. Вычислим x¢ и x¢¢:

;

.

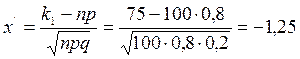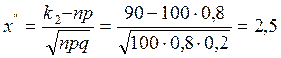Учитывая, что функция Лапласа нечетна, т.е. Ф(-x)=-Ф(x), получим

.

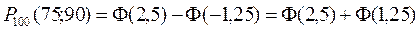По таблице значений функции 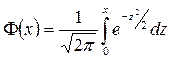  найдем:

Ф(2,5)=0,4938; Ф(1,25)=0,3944.

Искомая вероятность

Р₁₀₀(75;90)=0,4938+0,3944=0,8882.

б) требование, чтобы событие появилось не менее 75 раз, означает, что число появлений события может быть равно 75 либо 76, …, либо 100. Таким образом, в рассматриваемом случае следует принять k₁=75, k₂=100. Тогда

;

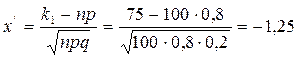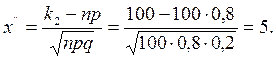
По таблице приложения 2 найдем Ф(1,25)=0,3944; Ф(5)=0,5.

Искомая вероятность

Р₁₀₀(75;100)=Ф(5)-Ф(-1,25)=Ф(5)+Ф(1,25)=0,5+0,3944=0,8944.

в) События – “А появилось не менее 75 раз” и “А появилось не более 74 раз” противовоположны, поэтому сумма вероятностей этих событий равна единице.

Следовательно, искомая вероятность Р₁₀₀(0;74)=1- Р₁₀₀(75;100)=1-0,8944=0,1056.

Задача №10

Вероятность появления события в каждом из 625 независимых испытаний равна 0,8. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,04.

Решение.

По условию, n=625; p=0,8; q=0,2; 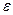=0,04.

Требуется найти вероятность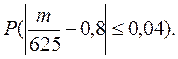

Воспользуемся формулой .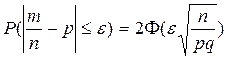

Имеем

.

По таблице приложения 2 найдем Ф(2,5)=0,4938. Следовательно, 2Ф(2,5)=2·0,4938=0,9876.

Ответ: искомая вероятность приближенно равна 0,9876.