Пусть событие А может наступить лишь при условии появления одного из несовместных событий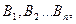 
которые образуют полную группу. Эти события называют ещё гипотезами. Известны вероятности гипотез 
и соответствующие условные вероятности события А 
.
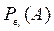Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий 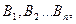образующих полную
группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
.
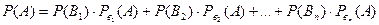Эта формула называется формулой полной вероятности.
Если событие А уже произошло, для нахождения так называемой переоценённой вероятности гипотез применяется формула Байеса:
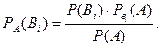
Повторные независимые испытания, формула Бернулли
Если производится несколько испытаний, причём вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.
Пусть производится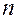 
независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Будем считать, что вероятность наступления события А в каждом испытании постоянна и равна p. Следовательно, вероятность ненаступления события А в каждом испытании равна q=1-p.
Вероятность того, что при 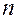независимых испытаниях интересующее нас событие наступит ровно 
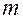раз определяется по формуле Бернулли
.
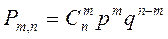Здесь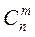 
- число сочетаний из 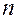элементов по 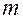, определяется по формуле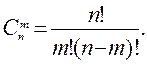 
Легко видеть, что пользоваться формулой Бернулли при больших значениях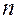 
достаточно трудно, так как требуется выполнение действий над громадными числами. Приведённая ниже теорема даёт асимптотическую формулу, которая позволяет приближённо найти вероятность появления события ровно 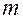раз при 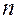испытаниях, если число испытаний достаточно велико.
Локальная теорема Лапласа
Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность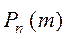 
того, что событие А появится в 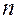испытаниях ровно 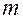раз приближённо определяется по формуле
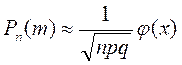при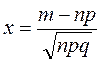 
.
Эта формула называется ещё формулой Муавра-Лапласа.
Значения функции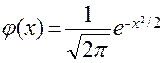 
находят по таблице (см. приложение 1) для положительных значений аргумента. Для отрицательных значений пользуются той же таблицей, так как функция 
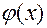чётна, т.е. 
.
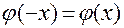Для вычисления вероятности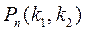 
того, что интересующее нас событие А появится в 
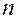испытаниях не менее 
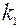и не более 
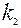раз применяется
Интегральная теорема Лапласа
Если вероятность р наступления события А в каждом испытании постоянна, отлична от нуля и единицы, то вероятность 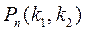того, что событие А появится в 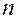испытаниях от 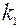до 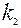раз, приближённо равна определённому интегралу
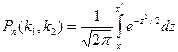
где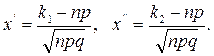 
Таблица для интеграла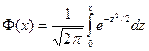 
приведена в приложении 2. Функцию 
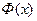называют функцией Лапласа. Она нечётна, т.е. 
.
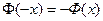Таким образом, искомая вероятность 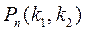попадания числа наступлений события А в заданный интервал равна разности значений функции Лапласа:
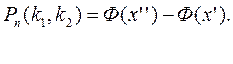
Распределение Пуассона
Пусть производится 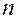независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности 
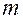появлений события в этих испытаниях используют формулу Бернулли. Если 
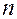велико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала (р 
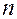0,1). В этих случаях ( велико, р мало) прибегают к асимптотической формуле Пуассона:
.
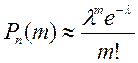Здесь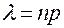 
сохраняет постоянное значение. Эта формула выражает закон распределения Пуассона вероятностей массовых ( 
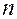велико) редких (р мало) событий. Число 
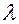есть среднее число событий, которые появляются в единицу времени. Тогда вероятность того, что за время t интересующее нас событие наступит ровно 
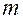раз при заданном 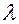определяется по формуле
.
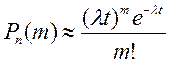Примеры решения задач типового расчета
Умножение вероятностей зависимых событий
Задача № 1
На десяти одинаковых карточках написаны различные цифры от 0 до 9. Определить вероятность того, что наудачу образованное из этих карточек 3-значное число делится на 5 (выборка без возвращения).
Решение
Первые две цифры могут быть любыми (первая отлична от 0), последней должен быть 0, либо 5. Следовательно, имеем одновременное выполнение трех условий, т.е. наступление трех событий, причем зависимых:
А – 1-я цифра любая, кроме 0;
В – 2-я цифра любая;
С – 3-я цифра 0, либо 5.
Тогда по теореме умножения вероятностей зависимых событий
.
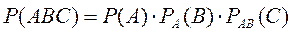
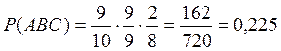Ответ: вероятность того, что образованное 3-значное число кратно 5 равна 0,225.
Задача № 2
За круглым столом 12 мест. 12 человек рассаживаются случайным образом. Найти вероятность того, что 2 определенных лица окажутся рядом.
Решение
Обозначим событие А – 2 определенных лица сядут рядом – как произведение двух событий: В – 1-й человек занял место (он может сесть на любой стул) и С – 2-й человек сел рядом с первым. Тогда А=В ∙ С. События В и С зависимы, поэтому Р(А) = Р(В) ∙ РВ(С).
Вероятность события В (1-й занял любое место) равна единице Р(В)=1
Вероятность события С при условии, что В произошло РВ(С) определяем как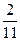 
(2-й может занять только 2 места из 11).
Тогда искомая вероятность Р(А) = Р(В) ∙ РВ(С)=1∙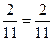 
=0,181.
Ответ: вероятность того, что 2 человека из 12 сядут рядом, равна 0,181.
Задача № 3
Слово М А Т Р О С разрезали на буквы, перемешали и извлекли 4 буквы. Найти вероятность того, что получилось слово Р О С А.
Решение.
I способ
Интересующее нас событие А – извлеченные буквы образуют слово РОСА есть произведение 4-х зависимых событий:
А1 – 1-я буква Р;
А2 – 2-я буква О;
А3 – 3-я буква С;
А4 – 4-я буква А.
Тогда по теореме умножения вероятностей зависимых событий имеем
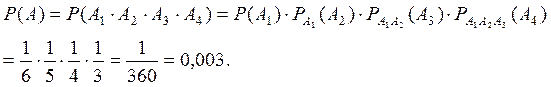
II способ
По классической формуле вероятности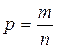 
, где m – число благоприятных исходов, n – общее число исходов.
Тогда в условиях данной задачи m=1 (слово РОСА можно образовать единственным способом из данного набора букв),
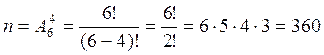
Окончательно имеем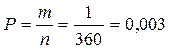 
.
Ответ: вероятность того, что наудачу взятые буквы образуют слово РОСА, равна 0,003.
Повторные независимые испытания, формула Бернулли.
Задача №4
Вероятность производства бракованной детали равна 0,008. Найти наивероятнейшее число бракованных среди 1000 деталей и вероятность такого количества их в партии.
Решение.
Наивероятнейшее число появлений события в n независимых испытаниях m0 определяем из условия np - q ≤ m0 < np + p.
Для нашей задачи n=1000, p=0,008, q=1-p=0,992.
Тогда 7,008 ≤ m0 < 8,008. Этому условию удовлетворяет целое число m0=8.
Найдем теперь вероятность того, что в партии из 1000 деталей равно 8 бракованных.
Поскольку число испытаний n=1000 достаточно велико, а p=0,008 достаточно мало, применим формулу Пуассона
,
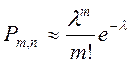где λ ≡ np – const – среднее число появлений события в одной серии испытаний.
Тогда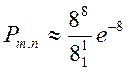 
≈ 0,14 - вероятность того, что в партии из 1000 деталей ровно 8 бракованных.
Задача № 5
Найти вероятность того, что при 5 бросках игральной кости 6 очков не выпадет ни разу.
Решение.
Вероятность наступления события при n независимых испытаниях m раз, находим по формуле Бернулли
,
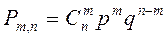где p – вероятность появления интересующего нас события при одном испытании, q – вероятность противоположного события.
Тогда в условиях нашей задачи
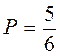(n=6, m=5, на верхней грани кубика любое число очков, кроме шести)
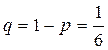. Применяя формулу Бернулли, получим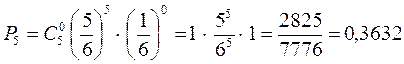 
Ответ: вероятность того, что при 5 бросках игральной кости 6 очков не выпадет ни разу, равна 0,3632.
Дата: 2019-02-02, просмотров: 271.
