ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Виды случайных событий
Случайным называется событие, которое при данных условиях может либо произойти, либо не произойти.
Например, событие “при бросании монеты выпал герб” – случайное.
Достоверным называют событие, которое обязательно произойдет в результате опыта.
Невозможным называется событие, которое заведомо не произойдет в условиях опыта.
Достаточно большое число однородных (т.е. происходящих при одних и тех же условиях) случайных событий подчиняется определенным, так называемым вероятностным закономерностям. Установлением этих закономерностей и занимается теория вероятностей.
События называются несовместными, если появление одного из них исключает появление других в одном и том же испытании. В противном случае события совместны.
Несовместные события А1, А2…Аn образуют полнуюгруппу, если в результате опыта обязательно происходит хотя бы одно из них.
Классическое определение вероятности
Вероятность является одним из основных понятий теории вероятностей.
Вероятностью события А называют отношение числа благоприятствующих этому событию исходов (m) к общему числу исходов (n).
Таким образом, вероятность события А определеяется по формуле
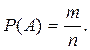
Суммой событий А и В называют событие А+В, состоящее либо в появлении А, либо в появлении В, либо в их совместном появлении.
Произведением событий А и В называют событие АВ, состоящее в совместном появлении этих событий.
Теорема сложения вероятностей несовместных событий
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
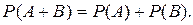
Теорема сложения вероятностей совместных событий
Вероятность появления хотя бы одного из двух совместных событий (т.е. вероятность их суммы) равна сумме вероятностей каждого в отдельности без вероятности их совместного появления:
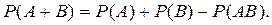
Теорема о вероятности полной группы событий
Сумма вероятностей событий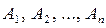 
, образующих полную группу, равна единице:
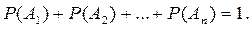
Таким образом сумма событий А1, А2…Аn есть событие достоверное.
Противоположными называют два единственно возможных события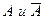 
, образующих полную группу.
Например, попадание и промах при одном выстреле – противоположные события.
Теорема о вероятностях противоположных событий
Сумма вероятностей противоположных событий равна единице:
.
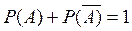Два события называют независимыми, если вероятность одного из них не зависит от появления или непоявления другого.
В противном случае события называют зависимыми.
Локальная теорема Лапласа
Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность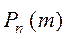 
того, что событие А появится в 
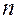испытаниях ровно 
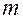раз приближённо определяется по формуле
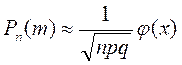при 
.
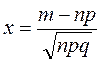Эта формула называется ещё формулой Муавра-Лапласа.
Значения функции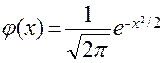 
находят по таблице (см. приложение 1) для положительных значений аргумента. Для отрицательных значений пользуются той же таблицей, так как функция 
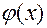чётна, т.е. 
.
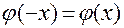Для вычисления вероятности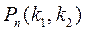 
того, что интересующее нас событие А появится в 
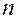испытаниях не менее 
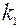и не более 
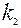раз применяется
Интегральная теорема Лапласа
Если вероятность р наступления события А в каждом испытании постоянна, отлична от нуля и единицы, то вероятность 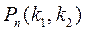того, что событие А появится в 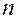испытаниях от 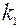до 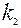раз, приближённо равна определённому интегралу
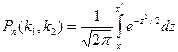
где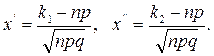 
Таблица для интеграла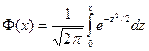 
приведена в приложении 2. Функцию 
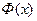называют функцией Лапласа. Она нечётна, т.е. 
.
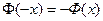Таким образом, искомая вероятность 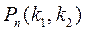попадания числа наступлений события А в заданный интервал равна разности значений функции Лапласа:
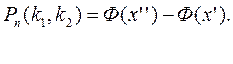
Распределение Пуассона
Пусть производится 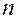независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности 
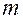появлений события в этих испытаниях используют формулу Бернулли. Если 
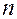велико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала (р 
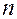0,1). В этих случаях ( велико, р мало) прибегают к асимптотической формуле Пуассона:
.
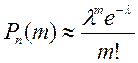Здесь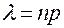 
сохраняет постоянное значение. Эта формула выражает закон распределения Пуассона вероятностей массовых ( 
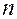велико) редких (р мало) событий. Число 
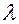есть среднее число событий, которые появляются в единицу времени. Тогда вероятность того, что за время t интересующее нас событие наступит ровно 
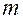раз при заданном 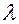определяется по формуле
.
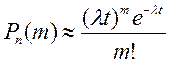Примеры решения задач типового расчета
Умножение вероятностей зависимых событий
Задача № 1
На десяти одинаковых карточках написаны различные цифры от 0 до 9. Определить вероятность того, что наудачу образованное из этих карточек 3-значное число делится на 5 (выборка без возвращения).
Решение
Первые две цифры могут быть любыми (первая отлична от 0), последней должен быть 0, либо 5. Следовательно, имеем одновременное выполнение трех условий, т.е. наступление трех событий, причем зависимых:
А – 1-я цифра любая, кроме 0;
В – 2-я цифра любая;
С – 3-я цифра 0, либо 5.
Тогда по теореме умножения вероятностей зависимых событий
.
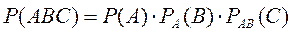
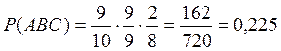Ответ: вероятность того, что образованное 3-значное число кратно 5 равна 0,225.
Задача № 2
За круглым столом 12 мест. 12 человек рассаживаются случайным образом. Найти вероятность того, что 2 определенных лица окажутся рядом.
Решение
Обозначим событие А – 2 определенных лица сядут рядом – как произведение двух событий: В – 1-й человек занял место (он может сесть на любой стул) и С – 2-й человек сел рядом с первым. Тогда А=В ∙ С. События В и С зависимы, поэтому Р(А) = Р(В) ∙ РВ(С).
Вероятность события В (1-й занял любое место) равна единице Р(В)=1
Вероятность события С при условии, что В произошло РВ(С) определяем как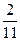 
(2-й может занять только 2 места из 11).
Тогда искомая вероятность Р(А) = Р(В) ∙ РВ(С)=1∙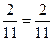 
=0,181.
Ответ: вероятность того, что 2 человека из 12 сядут рядом, равна 0,181.
Задача № 3
Слово М А Т Р О С разрезали на буквы, перемешали и извлекли 4 буквы. Найти вероятность того, что получилось слово Р О С А.
Решение.
I способ
Интересующее нас событие А – извлеченные буквы образуют слово РОСА есть произведение 4-х зависимых событий:
А1 – 1-я буква Р;
А2 – 2-я буква О;
А3 – 3-я буква С;
А4 – 4-я буква А.
Тогда по теореме умножения вероятностей зависимых событий имеем
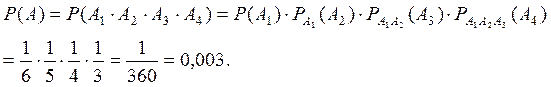
II способ
По классической формуле вероятности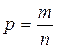 
, где m – число благоприятных исходов, n – общее число исходов.
Тогда в условиях данной задачи m=1 (слово РОСА можно образовать единственным способом из данного набора букв),
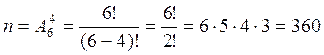
Окончательно имеем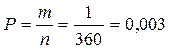 
.
Ответ: вероятность того, что наудачу взятые буквы образуют слово РОСА, равна 0,003.
Повторные независимые испытания, формула Бернулли.
Задача №4
Вероятность производства бракованной детали равна 0,008. Найти наивероятнейшее число бракованных среди 1000 деталей и вероятность такого количества их в партии.
Решение.
Наивероятнейшее число появлений события в n независимых испытаниях m0 определяем из условия np - q ≤ m0 < np + p.
Для нашей задачи n=1000, p=0,008, q=1-p=0,992.
Тогда 7,008 ≤ m0 < 8,008. Этому условию удовлетворяет целое число m0=8.
Найдем теперь вероятность того, что в партии из 1000 деталей равно 8 бракованных.
Поскольку число испытаний n=1000 достаточно велико, а p=0,008 достаточно мало, применим формулу Пуассона
,
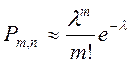где λ ≡ np – const – среднее число появлений события в одной серии испытаний.
Тогда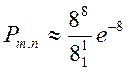 
≈ 0,14 - вероятность того, что в партии из 1000 деталей ровно 8 бракованных.
Задача № 5
Найти вероятность того, что при 5 бросках игральной кости 6 очков не выпадет ни разу.
Решение.
Вероятность наступления события при n независимых испытаниях m раз, находим по формуле Бернулли
,
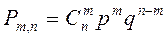где p – вероятность появления интересующего нас события при одном испытании, q – вероятность противоположного события.
Тогда в условиях нашей задачи
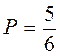(n=6, m=5, на верхней грани кубика любое число очков, кроме шести)
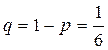. Применяя формулу Бернулли, получим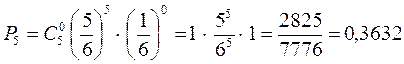 
Ответ: вероятность того, что при 5 бросках игральной кости 6 очков не выпадет ни разу, равна 0,3632.
Ответ:
1. Вероятность того, что из наугад взятой урны достали белый шар, равна 0,575.
2. Вероятность того, что белый шар оказался из четвертой урны, равна 0,348.
Распределение Пуассона
Задача №7
Корректура в 400 страниц содержит 800 опечаток. Найти вероятность того, что наугад взятая страница содержит 3 опечатки.
Решение.
Находим среднее число опечаток на одной странице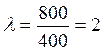 
Применяем формулу Пуассона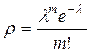 
для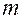 
=3. Получаем, что искомая вероятность равна 
.
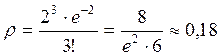Задача №8
Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
Решение.
По условию, n=243; k=70; p=0,25; q=0,75. Так как n=243 – достаточно большое число, воспользуемся локальной теоремой Лапласа:
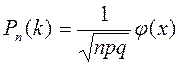, где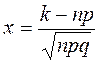 
.
Найдем значение x:
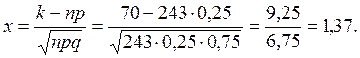
По таблице значений функции
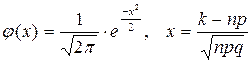
найдем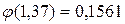 
.
Искомая вероятность
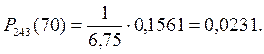
Ответ: вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, равна 0,0231.
Задача №9
Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна p=0,8. Найти вероятность того, что событие появится: а) не менее 75 раз и не более 90 раз; б) не менее 75 раз; в) не более 74 раз.
Решение.
Воспользуемся интегральной теоремой Лапласа:
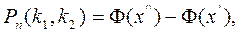где Ф(x) – функция Лапласа,
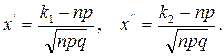
а) по условию, n=100; p=0,8; q=0,2; k1=75; k2=90. Вычислим x¢ и x¢¢:
;
.
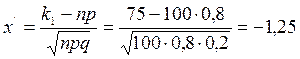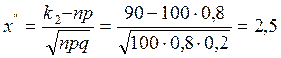Учитывая, что функция Лапласа нечетна, т.е. Ф(-x)=-Ф(x), получим
.
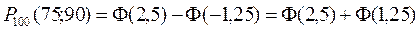По таблице значений функции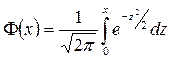 
найдем:
Ф(2,5)=0,4938; Ф(1,25)=0,3944.
Искомая вероятность
Р100(75;90)=0,4938+0,3944=0,8882.
б) требование, чтобы событие появилось не менее 75 раз, означает, что число появлений события может быть равно 75 либо 76, …, либо 100. Таким образом, в рассматриваемом случае следует принять k1=75, k2=100. Тогда
;
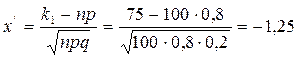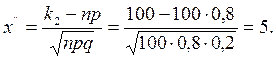
По таблице приложения 2 найдем Ф(1,25)=0,3944; Ф(5)=0,5.
Искомая вероятность
Р100(75;100)=Ф(5)-Ф(-1,25)=Ф(5)+Ф(1,25)=0,5+0,3944=0,8944.
в) События – “А появилось не менее 75 раз” и “А появилось не более 74 раз” противовоположны, поэтому сумма вероятностей этих событий равна единице.
Следовательно, искомая вероятность Р100(0;74)=1- Р100(75;100)=1-0,8944=0,1056.
Задача №10
Вероятность появления события в каждом из 625 независимых испытаний равна 0,8. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,04.
Решение.
По условию, n=625; p=0,8; q=0,2;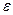 
=0,04.
Требуется найти вероятность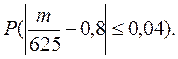 
Воспользуемся формулой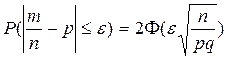 
.
Имеем
.
По таблице приложения 2 найдем Ф(2,5)=0,4938. Следовательно, 2Ф(2,5)=2·0,4938=0,9876.
Ответ: искомая вероятность приближенно равна 0,9876.
Задача «О шарах»
В урне 2 белых, 3 черных, 1 красный шар. Наудачу извлекают 2 шара. Найти вероятность того, что это будут белый и черный шары.
Решение.
I способ (шары извлекаются последовательно).
Рассмотрим интересующее нас событие А - появление одного черного и одного белого шара – как сумму событий А1 – первый шар белый, второй черный и А2 – первый черный, второй белый.
Тогда А= А1 + А2, т.е. событие А состоит в появлении либо события А1, либо события А2.
В свою очередь, А1 есть произведение (совместное наступление) событий В1 и С1:
В1 – первым извлекли белый шар,
С1 – вторым извлекли черный шар.
Поскольку В1 и С1 события зависимые, то P(A1)=P(B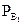1) ∙ 
(C1).
Найдем вероятность события B1.
Всего шаров в урне шесть, из них 2 белых. Следовательно, вероятность извлечь белый шар равна 2/6.
Найдем 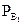(С1). Событие С1 наступает после события В1, в урне осталось 5 шаров, из них 3 черных.
Следовательно,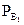 
(С1)=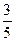 
.
Тогда P(A1)=P(B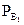1) ∙ (C1)=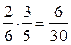 
.
Аналогично найдем вероятность события А2 (сначала черный, потом белый).
Введем события В2 и С2:
В2 ‑ первым появился черный шар,
С2 – вторым появился белый шар.
Тогда P(B2) =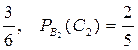 
и искомая вероятность P(A2)=P(B2) ∙ 
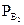(C2)=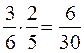 
.
Наконец, интересующая нас вероятность события А равна
P(A)=P(A1) + P(A2) =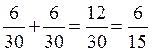 
.
II способ (шары извлекаются одновременно)
Согласно классической формуле вероятности P=m/n, где m - число благоприятных исходов, n – общее число исходов.
Общее число n исходов опыта в данной задаче (извлечение двух шаров из шести возможных) определяется числом способов, какими можно извлечь два шара из шести. Это число сочетаний из шести по два, n=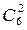 
.
При этом благоприятное число исходов m =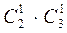 
- из двух белых извлекаем один { 
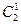} способами и из трех черных извлекаем один { 
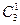} способами.
Применяя формулу сочетаний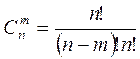 
, получим
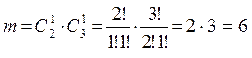
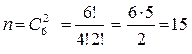. Окончательно, P= 
.
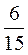Ответ: вероятность того, что из двух извлеченных наудачу шаров будет один белый и один черный, равна .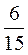
Задача «О лгунах»
В городе N жителей. Некто пустил слух, рассказав «новость» 1-му жителю. Тот рассказал следующему и т.д. Какова вероятность того, что 10-й житель расскажет «новость» тому, кто узнал ее первым.
Решение.
Для того, чтобы произошло интересующее нас событие А – 10-й житель рассказал «новость» первому, необходимо, чтобы первые девять этого не сделали. Очевидно, что первые два жителя из этих девяти не сделают этого с вероятностью, равной единице.
Остальные семь – с вероятностью, равной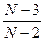 
. Десятый же расскажет «новость» первому с вероятностью 
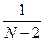, т.к. благоприятный исход один, общее - N-2, поскольку в общем случае новость рассказывается любому жителю из N за исключением того, от кого услышана.
Таким образом, искомая вероятность определяется как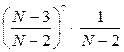 
.
ТИПОВЫЕ РАСЧЕТЫ
I вариант
1. Наудачу взятый телефонный номер состоит из 5 цифр. Какова вероятность того, что в нем все цифры нечетные.
2. N охотников договорились стрелять по дичи в такой последовательности: следующий стреляет лишь в случае промаха предыдущего. Вероятность попадания каждого равна ½. Найти вероятность того, что будет произведено 2 выстрела.
3. Слово Т О Л О К Н О разрезали на буквы, перемешали их и извлекли 3 буквы. Найти вероятность того, что получилось слово Т О Н.
4. Вероятность сработать автомату при опускании одной монеты неправильно – 0,01.
Найти наивероятнейшее число случаев правильной работы автомата, если опущено 200 монет.
5. Какова вероятность того, что при 10 бросках игральной кости три очка появятся ровно 1 раз?
6. Сборщик получил 2 коробки одинаковых деталей с завода №1 и 3 коробки деталей с завода №2. Вероятность того, что деталь завода №1 стандартна, равна 0,9, а завода №2 – 0,7. Из наудачу взятой коробки сборщик наудачу извлек деталь.
А. Найти вероятность того, что извлечена стандартная деталь.
В. Извлеченная деталь оказалась стандартной. Найти вероятность того, что она 1) с завода №1; 2) с завода №2.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 2. Применяя закон Пуассона, найти вероятность того, что за 2 минуты поступит 3 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,8. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 100 анализах будет получено ровно 75 положительных результатов.
9. В партии 60% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 200 деталей первосортных не менее 120 и не более 150 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,9, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,01.
Вероятность попадания при одном выстреле равна 0,8.
II вариант
1. Из десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 выбирают с возвратом 4 цифры.
Найти вероятность того, что в выборке все цифры одинаковые.
2. В ряду 10 стульев. Какова вероятность того, что при произвольном рассаживании десяти человек 3 определенных лица окажутся рядом?
3. Слово Б У Л А В К А разрезали на буквы, перемешали их и извлекли 4 буквы. Найти вероятность того, что получилось слово Л А В А.
4. Вероятность сработать автомату при опускании одной монеты неправильно – 0,02.
Найти наивероятнейшее число случаев правильной работы автомата, если опущено 100 монет.
5. Какова вероятность того, что при 10 бросках игральной кости число очков, кратное трем, появится ровно три раза?
6. Сборщик получил 2 коробки одинаковых деталей с завода №1 и 3 коробки деталей с завода №2. Вероятность того, что деталь завода №1 стандартна, равна 0,8, а завода №2 – 0,6. Из наудачу взятой коробки сборщик наудачу извлек деталь.
А. Найти вероятность того, что извлечена стандартная деталь.
В. Извлеченная деталь оказалась стандартной. Найти вероятность того, что она 1) с завода №1; 2) с завода №2.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 3. Применяя закон Пуассона, найти вероятность того, что за 1 минуту поступит 2 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,7. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 150 анализах будет получено ровно 100 положительных результатов.
9. В партии 50% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 300 деталей первосортных не менее 160 и не более 200 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,99, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,1.
Вероятность попадания при одном выстреле равна 0,9.
III вариант
1. На карточках написаны цифры от 1 до 9. Карточки перемешивают, наугад берут 4 из них и раскладывают в порядке появления. Какова вероятность получить при этом число 5678?
2. Двенадцать человек садятся за круглый стол. Какова вероятность того, что при этом два определенных лица сядут порознь?
3. Слово В О Д О Р О Д разрезали на буквы, перемешали и извлекли 4 буквы. Найти вероятность того, что получилось слово Д В О Р.
4. Чему равна вероятность наступления события в каждом испытании, если произведено 49 независимых испытаний, а наивероятнейшее число наступлений события из них равно 30?
5. Какова вероятность того, что при 10 бросках игральной кости три очка появятся ровно три раза?
6. Сборщик получил 2 коробки одинаковых деталей с завода №1 и 3 коробки деталей с завода №2. Вероятность того, что деталь завода №1 стандартна, равна 0,7, а завода №2 – 0,5. Из наудачу взятой коробки сборщик наудачу извлек деталь.
А. Найти вероятность того, что извлечена стандартная деталь.
В. Извлеченная деталь оказалась стандартной. Найти вероятность того, что она 1) с завода №1; 2) с завода №2.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 4. Применяя закон Пуассона, найти вероятность того, что за 0,5 минуты поступит 3 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,75. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 20 анализах будет получено ровно 13 положительных результатов.
9. В партии 70% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 400 деталей первосортных не менее 260 и не более 300 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,85, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,05.
Вероятность попадания при одном выстреле равна 0,8.
IV вариант
1. Из десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 выбирают с возвратом 4 цифры.
Найти вероятность того, что в выборке три цифры одинаковые.
2. В ряду 9 стульев. Какова вероятность того, что при произвольном рассаживании 9 человек 3 определенных лица окажутся рядом?
3. Слово П О Л О Т Н О разрезали на буквы, перемешали их и извлекли 3 буквы. Найти вероятность того, что получилось слово Л О Т.
4. Вероятность сработать автомату при опускании одной монеты неправильно – 0,02.
Найти наивероятнейшее число случаев правильной работы автомата, если опущено 200 монет.
5. Какова вероятность того, что при 10 бросках игральной кости число очков, кратное трем, появится ровно 4 раза?
6. Сборщик получил 2 коробки одинаковых деталей с завода №1 и 3 коробки деталей с завода №2. Вероятность того, что деталь завода №1 стандартна, равна 0,5, а завода №2 – 0,8. Из наудачу взятой коробки сборщик наудачу извлек деталь.
А. Найти вероятность того, что извлечена стандартная деталь.
В. Извлеченная деталь оказалась стандартной. Найти вероятность того, что она 1) с завода №1; 2) с завода №2.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 5. Применяя закон Пуассона, найти вероятность того, что за 0,2 минуты поступит 2 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,8. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 30 анализах будет получено ровно 20 положительных результатов.
9. В партии 80% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 500 деталей первосортных не менее 350 и не более 450 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,9, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,01.
Вероятность попадания при одном выстреле равна 0,9.
V вариант
1. Набирая номер телефона, абонент забыл последние две цифры, но помня, что эти цифры различны, набрал наугад. Определить вероятность того, что набраны нужные цифры.
2. Буквенный замок содержит на общей оси 4 диска, каждый из которых разделен на 6 секторов с различными нанесенными на них буквами. Замок открывается, когда каждый диск занимает определенное положение относительно корпуса замка.
Определить вероятность открытия замка, если установлена произвольная комбинация букв.
3. Слово С Е Р Е Б Р О разрезали на буквы, перемешали и извлекли 3 буквы. Найти вероятность того, что получилось слово Б О Р.
4. Вероятность сработать автомату при опускании одной монеты неправильно – 0,03. Найти наивероятнейшее число случаев правильной работы автомата, если опущено 150 монет.
5. Какова вероятность того, что при 10 бросках игральной кости три очка не выпадут ни разу?
6. Сборщик получил 2 коробки одинаковых деталей с завода №1 и 3 коробки деталей с завода №2. Вероятность того, что деталь завода №1 стандартна, равна 0,6, а завода №2 – 0,8. Из наудачу взятой коробки сборщик наудачу извлек деталь.
А. Найти вероятность того, что извлечена стандартная деталь.
В. Извлеченная деталь оказалась стандартной. Найти вероятность того, что она 1) с завода №1; 2) с завода №2.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 1. Применяя закон Пуассона, найти вероятность того, что за 3 минуты поступит 4 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,85. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 25 анализах будет получено ровно 22 положительных результатов.
9. В партии 90% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 600 деталей первосортных не менее 520 и не более 560 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,95, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,05.
Вероятность попадания при одном выстреле равна 0,8.
VI вариант
1. Из десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 выбирают с возвратом 4 цифры. Найти вероятность того, что в выборке только 2 одинаковые цифры.
2. В ряду 8 стульев. Какова вероятность того, что при произвольном рассаживании 8 человек 3 определенных лица окажутся рядом?
3. Слово С У Л Т А Н разрезали на буквы, перемешали и извлекли 4 буквы. Найти вероятность того, что получилось слово С Т А Н.
4. Вероятность сработать автомату при опускании одной монеты неправильно – 0,01.
Найти наивероятнейшее число случаев правильной работы автомата, если опущено 250 монет.
5. Производится 10 выстрелов по мишени. Вероятность попадания при одном выстреле 0,8. Найти вероятность ровно 5-ти попаданий.
6. Имеются три урны с шарами. В первой 4 белых и 3 черных, во второй 5 белых и 2 черных, в третьей 2 белых и 5 черных. Выбирают наугад одну из урн и вынимают 1 шар.
А. Найти вероятность того, что он белый.
В. Вынутый шар оказался белым. Найти вероятности того, что он:
1) из первой урны;
2) из второй урны;
3) из третьей урны.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 2. Применяя закон Пуассона, найти вероятность того, что за 2 минуты поступит 5 вызовов.
8. Вероятность положительного результата при химическом анализе равна 0,9. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 35 анализах будет получено ровно 30 положительных результатов.
9. В партии 40% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 100 деталей первосортных не менее 40 и не более 50 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,9, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,05.
Вероятность попадания при одном выстреле равна 0,7.
VII вариант
1. Наудачу взятый телефонный номер состоит из 5 цифр. Какова вероятность того, что в нем все цифры нечетные.
2. Из 11 билетов выигрышными являются 3. Определить вероятность того, что среди взятых наудачу четырех билетов два выигрышных.
3. Слово В Ы Б О Р К А разрезали на буквы, перемешали и извлекли 4 буквы. Найти вероятность того, что получилось слово К Р А Б.
4. Вероятность сработать автомату при опускании одной монеты неправильно – 0,03.
Найти наивероятнейшее число случаев правильной работы автомата, если опущено 50 монет.
5. Производится 10 выстрелов по мишени. Вероятность попадания при одном выстреле 0,8. Найти вероятность ровно 4-х попаданий.
6. Имеются три урны с шарами. В первой 3 белых и 7 черных, во второй 4 белых и 6 черных, в третьей 5 белых и 5 черных. Выбирают наугад одну из урн и вынимают 1 шар.
А. Найти вероятность того, что он белый.
В. Вынутый шар оказался белым. Найти вероятности того, что он:
1) из первой урны;
2) из второй урны;
3) из третьей урны.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 3. Применяя закон Пуассона, найти вероятность того, что за 1 минуту поступит 2 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,6. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 100 анализах будет получено ровно 55 положительных результатов.
9. В партии 30% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 200 деталей первосортных не менее 60 и не более 70 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,95, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,01.
Вероятность попадания при одном выстреле равна 0,75.
VIII вариант
1. Из десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 выбирают с возвратом 4 цифры. Найти вероятность того, что в выборке по 2 пары одинаковых цифр.
2. Семь человек случайным образом садятся на семь поставленных в ряд стульев. Какова вероятность того, что 3 определенных лица окажутся рядом?
3. Слово К Р Е П О С Т Ь разрезали на буквы, перемешали и извлекли 4 буквы. Найти вероятность того, что получилось слово П О С Т.
4. Сколько нужно взять деталей, чтобы наивероятнейшее число годных было равно 50, если вероятность наугад взятой детали оказаться бракованной равна 0,1?
5. Производится 10 выстрелов по мишени. Вероятность попадания при одном выстреле 0,9. Найти вероятность того, что будет не менее 5 попаданий.
6. Имеются три урны с шарами. В первой 4 белых и 5 черных, во второй 3 белых и 6 черных, в третьей 2 белых и 7 черных. Выбирают наугад одну из урн и вынимают 1 шар.
А. Найти вероятность того, что он белый.
В. Вынутый шар оказался белым. Найти вероятности того, что он:
1) из первой урны;
2) из второй урны;
3) из третьей урны.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 4. Применяя закон Пуассона, найти вероятность того, что за минуту поступит 2 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,65. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 40 анализах будет получено ровно 25 положительных результатов.
9. В партии 20% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 300 деталей первосортных не менее 50 и не более 60 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,9, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,05.
Вероятность попадания при одном выстреле равна 0,9.
IX вариант
1. На карточках написаны цифры от 1 до 9. Карточки перемешивают, наугад берут 4 из них и раскладывают в порядке появления. Какова вероятность получить нечетное число?
2. N охотников стреляют по дичи в такой последовательности: каждый стреляет лишь в случае промаха предыдущего. Вероятность попадания каждого – ½.
Найти вероятность того, что будет произведено N-2 выстрела.
3. Сколько перестановок можно получить из букв слова К О М И С С И Я?
Сколько перестановок начинается с первой буквы слова и кончается последней?
Сколько таких перестановок, в которых 2 одинаковые гласные стоят рядом?
4. Вероятность попадания в цель при одном выстреле – 0,8.
Найти наивероятнейшее число попаданий при 14 выстрелах.
5. Производится 10 выстрелов по мишеням. Вероятность попадания при одном выстреле 0,9.
Найти вероятность того, что будет не менее 9 попаданий.
6. Имеются три урны с шарами. В первой 4 белых и 4 черных, во второй 3 белых и 5 черных, в третьей 2 белых и 6 черных. Выбирают наугад одну из урн и вынимают 1 шар.
А. Найти вероятность того, что он белый.
В. Вынутый шар оказался белым. Найти вероятности того, что он:
1) из первой урны; 2) из второй урны; 3) из третьей урны.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 5. Применяя закон Пуассона, найти вероятность того, что за 0,2 минуты поступит 3 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,5. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 45 анализах будет получено ровно 20 положительных результатов.
9. В партии 10% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 400 деталей первосортных не менее 35 и не более 45 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,85, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,01.
Вероятность попадания при одном выстреле равна 0,9.
X вариант
1. Из десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 выбирают с возвратом 4 цифры.
Найти вероятность того, что в выборке все цифры разные.
2. Буквенный замок содержит на общей оси 3 диска, каждый из которых разделен на 8 секторов с различными нанесенными на них буквами. Замок открывается, когда каждый диск занимает определенное положение относительно корпуса замка. Определить вероятность открытия замка, если установлена произвольная комбинация букв.
3. Слово К В А Р Т И Р А разрезали на буквы, перемешали и извлекли 3 буквы. Найти вероятность того, что получилось слово Т И Р .
4. Вероятность изготовления стандартной детали в некоторых условиях – 0,98. Найти наивероятнейшее число стандартных деталей из 625.
5. Какова вероятность того, что при десяти бросаниях монеты «орел» выпадет ровно пять раз?
6. Имеются три урны с шарами. В первой 2 белых и 4 черных, во второй 3 белых и 3 черных, в третьей 1 белых и 5 черных. Выбирают наугад одну из урн и вынимают 1 шар.
А. Найти вероятность того, что он белый.
В. Вынутый шар оказался белым. Найти вероятности того, что он:
1) из первой урны;
2) из второй урны;
3) из третьей урны.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 6. Применяя закон Пуассона, найти вероятность того, что за 0,5 минуты поступит 4 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,55. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 50 анализах будет получено ровно 25 положительных результатов.
9. В партии 75% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 500 деталей первосортных не менее 350 и не более 400 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,99, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,1.
Вероятность попадания при одном выстреле равна 0,7.
XI вариант
1. Производится прием кодовых операций, содержащих 4 цифры от 1 до 4. Определить вероятность того, что в принятой комбинации цифры образуют последовательность 1, 2, 3, 4.
2. Из 10 билетов выигрышными являются 2. Определить вероятность того, что среди взятых наудачу пяти билетов один выигрышный.
3. Из букв слова М У Ж Е С Т В О составляются четырехбуквенные слова.
Определить:
а) сколько таких слов можно получить?
б) сколько таких слов начинается с буквы «М»?
в) сколько таких слов заканчивается гласной буквой?
4. Вероятность сработать автомату при опускании одной монеты неправильно – 0,01. Найти наивероятнейшее число случаев правильной работы автомата, если опущено 250 монет.
5. Вероятность попадания по быстродвижущейся цели при автоматической наводке орудия равна 0,7. Определить вероятность 5 попаданий при 10 выстрелах.
6. Радиолампа, поставленная в телевизор, может принадлежать одной из трех партий с вероятностями 0,2; 0,5; 0,3. Вероятности того, что лампа проработает определенное число часов, равны соответственно 0,1; 0,2; 0,4.
А. Определить вероятность того, что наугад взятая лампа проработает заданное число часов.
В. Наугад взятая лампа проработала заданное число часов. Найти вероятность того, что 1) лампа принадлежит 1-й партии;
2) 2-й партии; 3) 3-й партии.
7. Корректура в 500 страниц содержит 1500 опечаток. Применяя закон Пуассона, найти вероятность того, что наудачу взятая страница содержит 1 опечатку.
8. Вероятность положительного результата при химическом анализе равна 0,7. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 30 анализах будет получено ровно 25 положительных результатов.
9. В партии 70% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 1000 деталей первосортных не менее 500 и не более 700 штук.
10. Применяя теорему Бернулли, определить вероятность того, что при 40 выстрелах по мишени относительная частота попаданий отклонится от постоянной вероятности, не более чем на 0,01.
Вероятность попадания при одном выстреле равна 0,7.
XII вариант
1. Производится прием кодовых операций, содержащих 4 цифры от 1 до 4. Определить вероятность того, что в принятой последовательности цифра 1 оказалась последней.
2. Из 15-ти билетов выигрышными являются 3. Определить вероятность того, что среди взятых наудачу четырех билетов один выигрышный.
3. Из букв слова М У З Ы К А Н Т составляются четырехбуквенные слова.
Определить:
а) сколько таких слов можно получить?
б) сколько таких слов начинается с буквы «М»?
в) сколько таких слов заканчивается гласной буквой?
4. Вероятность попадания в цель при одном выстреле – 0,9.
Найти наивероятнейшее число попаданий при 15 выстрелах.
5. Вероятность того, что кинокамера, взятая напрокат, будет возвращена исправной, равна 0,8. Какова вероятность того, что из 4-х кинокамер, взятых напрокат, три окажутся неисправными?
6. Радиолампа, поставленная в телевизор, может принадлежать одной из трех партий с вероятностями 0,4; 0,5; 0,1. Вероятности того, что лампа проработает определенное число часов, равны соответственно 0,7; 0,8; 0,9.
А. Определить вероятность того, что наугад взятая лампа проработает заданное число часов.
В. Наугад взятая лампа проработала заданное число часов.
Найти вероятность того, что 1) лампа принадлежит 1-й партии;
2) 2-й партии;
3) 3-й партии.
7. Корректура в 600 страниц содержит 1200 опечаток. Применяя закон Пуассона, найти вероятность того, что наудачу взятая страница содержит 1 опечатку.
8. Вероятность положительного результата при химическом анализе равна 0,8. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 35 анализах будет получено ровно 24 положительных результатов.
9. В партии 80% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 900 деталей первосортных не менее 700 и не более 800 штук.
10. Применяя теорему Бернулли, определить вероятность того, что при 30 выстрелах по мишени относительная частота попаданий отклонится от постоянной вероятности не более чем на 0,01.
Вероятность попадания при одном выстреле равна 0,7.
XIII вариант
1. Определить вероятность того, что номер первой встречающейся автомашины не содержит одинаковых цифр.
2. Из 15 билетов выигрышными являются 3. Определить вероятность того, что среди взятых наудачу шести билетов: а) оба выигрышных; б) оба проигрышных.
3. Из букв слова М У Ш К Е Т Е Р составляются четырехбуквенные слова.
Определить:
а) сколько таких слов можно получить?
б) сколько таких слов начинается с буквы «М»?
в) сколько таких слов заканчивается гласной буквой?
4. В результате многолетних наблюдений для некоторой местности было установлено, что вероятность первого июля быть дождливым днем равна 0,4. Найти наивероятнейшее число дождливых дней первого июля за ближайшие 50 лет.
5. Вероятность попадания в цель при одном выстреле – 0,85.
Найти вероятность 8 попаданий при 10 выстрелах.
6. Радиолампа, поставленная в телевизор, может принадлежать одной из трех партий с вероятностями 0,1; 0,2; 0,7. Вероятности того, что лампа проработает определенное число часов, равны соответственно 0,6; 0,7; 0,8.
А. Определить вероятность того, что наугад взятая лампа проработает заданное число часов.
В. Наугад взятая лампа проработала заданное число часов.
Найти вероятность того, что
1) лампа принадлежит 1-й партии;
2) 2-й партии; 3) 3-й партии.
7. Корректура в 700 страниц содержит 1400 опечаток. Применяя закон Пуассона, найти вероятность того, что наудачу взятая страница содержит 2 опечатки.
8. Вероятность положительного результата при химическом анализе равна 0,6. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 40 анализах будет получено ровно 30 положительных результатов.
9. В партии 60% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 800 деталей первосортных не менее 480 и не более 500 штук.
10. Применяя теорему Бернулли, определить вероятность того, что при 50 выстрелах по мишени относительная частота попаданий отклонится от постоянной вероятности не более чем на 0,05.
Вероятность попадания при одном выстреле равна 0,8.
XIV вариант
1. В книге 500 страниц. Какова вероятность того, что наугад открытая страница будет иметь порядковый номер, кратный 7?
2. Из колоды (52 карты) наугад извлекаются три карты. Определить вероятность того, что все они одной масти.
3. Из букв слова М Я Т Е Ж Н И К составляются четырехбуквенные слова.
Определить:
а) сколько таких слов можно получить?
б) сколько таких слов начинается с буквы «М»?
в) сколько таких слов заканчивается гласной буквой?
4. Вероятность попадания в цель при одном выстреле – 0,9.
Найти наивероятнейшее число попаданий при 10 выстрелах.
5. Производство дает такие изделия, для каждого из которых вероятность быть бракованным равна 0,1. На испытание наугад отобрано 4 изделия. Определить вероятность того, что среди них бракованных не более одного.
6. Радиолампа, поставленная в телевизор, может принадлежать одной из трех партий с вероятностями 0,6; 0,2; 0,2. Вероятности того, что лампа проработает определенное число часов, равны соответственно 0,5; 0,6; 0,7.
А. Определить вероятность того, что наугад взятая лампа проработает заданное число часов.
В. Наугад взятая лампа проработала заданное число часов.
Найти вероятность того, что
1) лампа принадлежит 1-й партии;
2) 2-й партии;
3) 3-й партии.
7. Корректура в 500 страниц содержит 1000 опечаток. Применяя закон Пуассона, найти вероятность того, что наудачу взятая страница содержит 1 опечатку.
8. Вероятность положительного результата при химическом анализе равна 0,9. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 45 анализах будет получено ровно 35 положительных результатов.
9. В партии 75% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 700 деталей первосортных не менее 500 и не более 550 штук.
10. Применяя теорему Бернулли, определить вероятность того, что при 40 выстрелах по мишени относительная частота попаданий отклонится от постоянной вероятности не более чем на 0,01.
Вероятность попадания при одном выстреле равна 0,75.
XV вариант
1. На карточках написаны цифры от 1 до 9. Карточки перемешивают, наугад берут 4 из них и раскладывают в порядке появления. Какова вероятность получить при этом число 1234?
2. Из колоды (52 карты) наугад извлекаются (без возвращения) четыре карты. Определить вероятность того, что это валет, дама, король и туз.
3. Из букв слова М А Г Н Е З И Я составляются четырехбуквенные слова.
Определить:
а) сколько таких слов можно получить?
б) сколько таких слов начинается с буквы «М»?
в) сколько таких слов заканчивается гласной буквой?
4. Вероятность попадания в цель при одном выстреле – 0,7.
Найти наивероятнейшее число попаданий при 20 выстрелах.
5. Для каждого мотора в цехе вероятность быть включенным равна 0,5. Сколько всего моторов в цехе, если с вероятностью, равной 5/16, можно утверждать, что в данный момент включено два мотора.
6. Радиолампа, поставленная в телевизор, может принадлежать одной из трех партий с вероятностями 0,1; 0,8; 0,1. Вероятности того, что лампа проработает определенное число часов, равны соответственно 0,4; 0,5; 0,6.
А. Определить вероятность того, что наугад взятая лампа проработает заданное число часов.
В. Наугад взятая лампа проработала заданное число часов.
Найти вероятность того, что 1) лампа принадлежит 1-й партии;
2) 2-й партии;
3) 3-й партии.
7. Корректура в 1000 страниц содержит 1000 опечаток. Применяя закон Пуассона, найти вероятность того, что наудачу взятая страница содержит 2 опечатки.
8. Вероятность положительного результата при химическом анализе равна 0,4. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 50 анализах будет получено ровно 25 положительных результатов.
9. В партии 65% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 600 деталей первосортных не менее 390 и не более 400 штук.
10. Применяя теорему Бернулли, определить вероятность того, что при 30 выстрелах по мишени относительная частота попаданий отклонится от постоянной вероятности не более чем на 0,02.
Вероятность попадания при одном выстреле равна 0,85.
XVI вариант
1. На карточках написаны цифры от 1 до 9. Карточки перемешивают, наугад берут 4 из них и раскладывают в порядке появления. Какова вероятность получить четное число?
2. Из колоды в 36 карт наудачу извлекают 3 карты. Определить вероятность того, что все они разной масти.
3. Из букв слова М А Г Н О Л И Я составляются четырехбуквенные слова.
Определить:
а) сколько таких слов можно получить?
б) сколько таких слов начинается с буквы «М»?
в) сколько таких слов заканчивается гласной буквой?
4. Вероятность попадания в цель при одном выстреле – 0,75.
Найти наивероятнейшее число попаданий при 30 выстрелах.
5. В результате длительной проверки на деревообделочным заводе было установлено, что вероятность выпуска бракованного оконного блока равна 0,2. Найти вероятность 2 бракованных блоков в партии из 10 штук.
6. Сборщик получил 3 ящика деталей: в первом 40 деталей, из них 20 окрашенных; во втором – 50, из них 10 окрашенных, в третьем – 30 деталей, из них 15 окрашенных.
А. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика окажется окрашенной.
В. Извлеченная деталь оказалась окрашенной. Найти вероятность того, что она 1) из I – го ящика;
2) из II – го ящика;
3) из III – го ящика.
7. Корректура в 600 страниц содержит 1200 опечаток. Применяя закон Пуассона, найти вероятность того, что наудачу взятая страница содержит 2 опечатки.
8. Вероятность положительного результата при химическом анализе равна 0,5. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 60 анализах будет получено ровно 35 положительных результатов.
9. В партии 55% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 500 деталей первосортных не менее 250 и не более 300 штук.
10. Применяя теорему Бернулли, определить вероятность того, что при 50 выстрелах по мишени относительная частота попаданий отклонится от постоянной вероятности не более чем на 0,03.
Вероятность попадания при одном выстреле равна 0,9.
XVII вариант
1. Наудачу взятый телефонный номер состоит из 5 цифр. Какова вероятность того, что в нем все цифры разные.
2. Из колоды в 36 карт наудачу извлекают 4 карты. Определить вероятность того, что все они разной масти.
3. Из букв слова М Е Д Я Ш К А составляются четырехбуквенные слова.
Определить:
а) сколько таких слов можно получить?
б) сколько таких слов начинается с буквы «М»?
в) сколько таких слов заканчивается гласной буквой?
4. Вероятность попадания в цель при одном выстреле – 0,95.
Найти наивероятнейшее число попаданий при 20 выстрелах.
5. В типографии четыре печатающих устройства. Вероятность того, что одно какое-то устройство в данный момент работает, равна 0,8. Какова вероятность того, что в данный момент работают 3 печатающих устройства?
6. Сборщик получил 3 ящика деталей: в первом 20 деталей, из них 10 окрашенных; во втором – 30, из них 20 окрашенных, в третьем – 15 деталей, из них 5 окрашенных.
А. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика окажется окрашенной.
В. Извлеченная деталь оказалась окрашенной. Найти вероятность того, что она 1) из I – го ящика;
2) из II – го ящика;
3) из III – го ящика.
7. Корректура в 700 страниц содержит 1400 опечаток. Применяя закон Пуассона, найти вероятность того, что наудачу взятая страница содержит 1 опечатку.
8. Вероятность положительного результата при химическом анализе равна 0,6. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 70 анализах будет получено ровно 40 положительных результатов.
9. В партии 45% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 400 деталей первосортных не менее 160 и не более 180 штук.
10. Применяя теорему Бернулли, определить вероятность того, что при 20 выстрелах по мишени относительная частота попаданий отклонится от постоянной вероятности не более чем на 0,04.
Вероятность попадания при одном выстреле равна 0,75.
XVIII вариант
1. Определить вероятность того, что номер первой встречающейся автомашины состоит из одинаковых цифр.
2. Из колоды в 36 карт наудачу извлекают 4 карты. Определить вероятность того, что среди них 2 карты бубновой и 2 карты червонной масти.
3. Из букв слова М А Н И Ф Е С Т составляются четырехбуквенные слова.
Определить:
а) сколько таких слов можно получить?
б) сколько таких слов начинается с буквы «М»?
в) сколько таких слов заканчивается гласной буквой?
4. Вероятность попадания в цель при одном выстреле – 0,95.
Найти наивероятнейшее число попаданий при 30 выстрелах.
5. Студент заочник получает учебники по почте. Вероятность того, что учебник имеет твердый переплет, равна 0,8. Определить вероятность того, что из 5-ти учебников, высланных студенту, без твердого переплета будет три учебника.
6. Сборщик получил 3 ящика деталей: в первом 25 деталей, из них 5 окрашенных; во втором – 35, из них 7 окрашенных, в третьем – 45 деталей, из них 9 окрашенных.
А. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика окажется окрашенной.
В. Извлеченная деталь оказалась окрашенной. Найти вероятность того, что она 1) из I – го ящика;
2) из II – го ящика;
3) из III – го ящика.
7. Корректура в 500 страниц содержит 1000 опечаток. Применяя закон Пуассона, найти вероятность того, что наудачу взятая страница содержит 2 опечатки.
8. Вероятность положительного результата при химическом анализе равна 0,7. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 80 анализах будет получено ровно 60 положительных результатов.
9. В партии 85% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 300 деталей первосортных не менее 240 и не более 260 штук.
10. Применяя теорему Бернулли, определить вероятность того, что при 25 выстрелах по мишени относительная частота попаданий отклонится от постоянной вероятности не более чем на 0,05.
Вероятность попадания при одном выстреле равна 0,7.
XIX вариант
1. Набирая номер телефона, абонент забыл последние две цифры, но помня, что эти цифры различны, набрал наугад. Определить вероятность того, что нужные цифры переставлены местами.
2. Из колоды в 36 карт наудачу извлекают 4 карты. Определить вероятность того, что среди них нет карт трефовой масти.
3. Из букв слова М А Н И К Ю Р составляются четырехбуквенные слова.
Определить:
а) сколько таких слов можно получить?
б) сколько таких слов начинается с буквы «М»?
в) сколько таких слов заканчивается гласной буквой?
4. Вероятность попадания в цель при одном выстреле – 0,95.
Найти наивероятнейшее число попаданий при 15 выстрелах.
5. Студент заочник получает учебники по почте. Вероятность того, что учебник имеет твердый переплет, равна 0,9. Определить вероятность того, что из 4-х учебников, высланных студенту, без твердого переплета будет три учебника.
6. Сборщик получил 3 ящика деталей: в первом 30 деталей, из них 6 окрашенных; во втором – 40, из них 5 окрашенных, в третьем – 28 деталей, из них 7 окрашенных.
А. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика окажется окрашенной.
В. Извлеченная деталь оказалась окрашенной. Найти вероятность того, что она 1) из I – го ящика;
2) из II – го ящика;
3) из III – го ящика.
7. Корректура в 800 страниц содержит 800 опечаток. Применяя закон Пуассона, найти вероятность того, что наудачу взятая страница содержит 2 опечатки.
8. Вероятность положительного результата при химическом анализе равна 0,8. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 90 анализах будет получено ровно 70 положительных результатов.
9. В партии 25% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 320 деталей первосортных не менее 60 и не более 80 штук.
10. Применяя теорему Бернулли, определить вероятность того, что при 30 выстрелах по мишени относительная частота попаданий отклонится от постоянной вероятности не более чем на 0,06.
Вероятность попадания при одном выстреле равна 0,8.
XX вариант
1. На десяти одинаковых карточках написаны различные цифры от 0 до 9. Определить вероятность того, что наудачу образованное из этих карточек двузначное число делится на 18 (выборка без возвращения).
2. Из колоды в 36 карт наудачу извлекают 4 карты. Найти вероятность того, что это 4 туза.
3. Из букв слова М Е Д О В А Р составляются четырехбуквенные слова.
Определить:
а) сколько таких слов можно получить?
б) сколько таких слов начинается с буквы «М»?
в) сколько таких слов заканчивается гласной буквой?
4. Вероятность сработать автомату при опускании одной монеты неправильно – 0,01.
Найти наивероятнейшее число случаев правильной работы автомата, если опущено 150 монет.
5. Какова должна быть вероятность попадания при одном выстреле, чтобы с вероятностью, равной 0,8, можно было утверждать, что из трех выстрелов не будет ни одного попадания?
6. Сборщик получил 3 ящика деталей: в первом 15 деталей, из них 3 окрашенных; во втором – 18, из них 6 окрашенных, в третьем – 21 деталей, из них 7 окрашенных.
А. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика окажется окрашенной.
В. Извлеченная деталь оказалась окрашенной. Найти вероятность того, что она 1) из I – го ящика;
2) из II – го ящика;
3) из III – го ящика.
7. Корректура в 800 страниц содержит 1600 опечаток. Применяя закон Пуассона, найти вероятность того, что наудачу взятая страница содержит 1 опечатку.
8. Вероятность положительного результата при химическом анализе равна 0,4. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 70 анализах будет получено ровно 30 положительных результатов.
9. В партии 35% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 600 деталей первосортных не менее 200 и не более 220 штук.
10. Применяя теорему Бернулли, определить вероятность того, что при 35 выстрелах по мишени относительная частота попаданий отклонится от постоянной вероятности не более чем на 0,07. Вероятность попадания при одном выстреле равна 0,9.
ЛИТЕРАТУРА
Список основной литературы
1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшее образование, 2008.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, часть II. – М.: ОНИКС, 2005.
Приложение 1
Таблица значений функции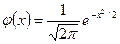 
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0,0 | 0,3989 | 0,3989 | 0,3989 | 0,3988 | 0,3986 | 0,3984 | 0,3982 | 0,3980 | 0,3977 | 0,3973 |
| 0,1 | 0,3970 | 0,3965 | 0,3961 | 0,3956 | 0,3951 | 0,3945 | 0,3939 | 0,3932 | 0,3925 | 0,3918 |
| 0,2 | 0,3910 | 0,3902 | 0,3894 | 0,3885 | 0,3876 | 0,3867 | 0,3857 | 0,3847 | 0,3836 | 0,3825 |
| 0,3 | 0,3814 | 0,3802 | 0,3790 | 0,3778 | 0,3765 | 0,3752 | 0,3739 | 0,3726 | 0,3712 | 0,3697 |
| 0,4 | 0,3683 | 0,3668 | 0,3652 | 0,3637 | 0,3621 | 0,3605 | 0,3589 | 0,3572 | 0,3555 | 0,3538 |
| 0,5 | 0,3521 | 0,3503 | 0,3485 | 0,3467 | 0,3448 | 0,3429 | 0,3410 | 0,3391 | 0,3372 | 0,3352 |
| 0,6 | 0,3332 | 0,3312 | 0,3292 | 0,3271 | 0,3251 | 0,3230 | 0,3209 | 0,3187 | 0,3166 | 0,3144 |
| 0,7 | 0,3123 | 0,3101 | 0,3079 | 0,3056 | 0,3034 | 0,3011 | 0,2989 | 0,2966 | 0,2943 | 0,2920 |
| 0,8 | 0,2897 | 0,2874 | 0,2850 | 0,2827 | 0,2803 | 0,2780 | 0,2756 | 0,2732 | 0,2709 | 0,2685 |
| 0,9 | 0,2661 | 0,2637 | 0,2613 | 0,2589 | 0,2565 | 0,2541 | 0,2516 | 0,2492 | 0,2468 | 0,2444 |
| 1 | 0,2420 | 0,2396 | 0,2371 | 0,2347 | 0,2323 | 0,2299 | 0,2275 | 0,2251 | 0,2227 | 0,2203 |
| 1,1 | 0,2179 | 0,2155 | 0,2131 | 0,2107 | 0,2083 | 0,2059 | 0,2036 | 0,2012 | 0,1989 | 0,1965 |
| 1,2 | 0,1942 | 0,1919 | 0,1895 | 0,1872 | 0,1849 | 0,1826 | 0,1804 | 0,1781 | 0,1758 | 0,1736 |
| 1,3 | 0,1714 | 0,1691 | 0,1669 | 0,1647 | 0,1626 | 0,1604 | 0,1582 | 0,1561 | 0,1539 | 0,1518 |
| 1,4 | 0,1497 | 0,1476 | 0,1456 | 0,1435 | 0,1415 | 0,1394 | 0,1374 | 0,1354 | 0,1334 | 0,1315 |
| 1,5 | 0,1295 | 0,1276 | 0,1257 | 0,1238 | 0,1219 | 0,1200 | 0,1182 | 0,1163 | 0,1145 | 0,1127 |
| 1,6 | 0,1109 | 0,1092 | 0,1074 | 0,1057 | 0,1040 | 0,1023 | 0,1006 | 0,0989 | 0,0973 | 0,0957 |
| 1,7 | 0,0940 | 0,0925 | 0,0909 | 0,0893 | 0,0878 | 0,0863 | 0,0848 | 0,0833 | 0,0818 | 0,0804 |
| 1,8 | 0,0790 | 0,0775 | 0,0761 | 0,0748 | 0,0734 | 0,0721 | 0,0707 | 0,0694 | 0,0681 | 0,0669 |
| 1,9 | 0,0656 | 0,0644 | 0,0632 | 0,0620 | 0,0608 | 0,0596 | 0,0584 | 0,0573 | 0,0562 | 0,0551 |
| 2 | 0,0540 | 0,0529 | 0,0519 | 0,0508 | 0,0498 | 0,0488 | 0,0478 | 0,0468 | 0,0459 | 0,0449 |
| 2,1 | 0,0440 | 0,0431 | 0,0422 | 0,0413 | 0,0404 | 0,0396 | 0,0387 | 0,0379 | 0,0371 | 0,0363 |
| 2,2 | 0,0355 | 0,0347 | 0,0339 | 0,0332 | 0,0325 | 0,0317 | 0,0310 | 0,0303 | 0,0297 | 0,0290 |
| 2,3 | 0,0283 | 0,0277 | 0,0270 | 0,0264 | 0,0258 | 0,0252 | 0,0246 | 0,0241 | 0,0235 | 0,0229 |
| 2,4 | 0,0224 | 0,0219 | 0,0213 | 0,0208 | 0,0203 | 0,0198 | 0,0194 | 0,0189 | 0,0184 | 0,0180 |
| 2,5 | 0,0175 | 0,0171 | 0,0167 | 0,0163 | 0,0158 | 0,0154 | 0,0151 | 0,0147 | 0,0143 | 0,0139 |
| 2,6 | 0,0136 | 0,0132 | 0,0129 | 0,0126 | 0,0122 | 0,0119 | 0,0116 | 0,0113 | 0,0110 | 0,0107 |
| 2,7 | 0,0104 | 0,0101 | 0,0099 | 0,0096 | 0,0093 | 0,0091 | 0,0088 | 0,0086 | 0,0084 | 0,0081 |
| 2,8 | 0,0079 | 0,0077 | 0,0075 | 0,0073 | 0,0071 | 0,0069 | 0,0067 | 0,0065 | 0,0063 | 0,0061 |
| 2,9 | 0,0060 | 0,0058 | 0,0056 | 0,0055 | 0,0053 | 0,0051 | 0,0050 | 0,0048 | 0,0047 | 0,0043 |
| 3 | 0,0044 | 0,0043 | 0,0042 | 0,0040 | 0,0039 | 0,0038 | 0,0037 | 0,0036 | 0,0035 | 0,0034 |
| 3,1 | 0,0033 | 0,0032 | 0,0031 | 0,0030 | 0,0029 | 0,0028 | 0,0027 | 0,0026 | 0,0025 | 0,0025 |
| 3,2 | 0,0024 | 0,0023 | 0,0022 | 0,0022 | 0,0021 | 0,0020 | 0,0020 | 0,0019 | 0,0018 | 0,0018 |
| 3,3 | 0,0017 | 0,0017 | 0,0016 | 0,0016 | 0,0015 | 0,0015 | 0,0014 | 0,0014 | 0,0013 | 0,0013 |
| 3,4 | 0,0012 | 0,0012 | 0,0012 | 0,0011 | 0,0011 | 0,0010 | 0,0010 | 0,0010 | 0,0009 | 0,0009 |
| 3,5 | 0,0009 | 0,0008 | 0,0008 | 0,0008 | 0,0008 | 0,0007 | 0,0007 | 0,0007 | 0,0007 | 0,0006 |
| 3,6 | 0,0006 | 0,0006 | 0,0006 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0004 |
| 3,7 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0003 | 0,0003 | 0,0003 | 0,0003 |
| 3,8 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 |
| 3,9 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0001 | 0,0001 |
Приложение 2
Таблица значений функции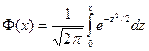 
| x | Ф(х) | x | Ф(х) | x | Ф(х) | x | Ф(х) |
| 0 | 0,0000 | 0,43 | 0,1664 | 0,86 | 0,3051 | 1,29 | 0,4015 |
| 0,01 | 0,0040 | 0,44 | 0,1700 | 0,87 | 0,3078 | 1,3 | 0,4032 |
| 0,02 | 0,0080 | 0,45 | 0,1736 | 0,88 | 0,3106 | 1,31 | 0,4049 |
| 0,03 | 0,0120 | 0,46 | 0,1772 | 0,89 | 0,3133 | 1,32 | 0,4066 |
| 0,04 | 0,0160 | 0,47 | 0,1808 | 0,9 | 0,3159 | 1,33 | 0,4082 |
| 0,05 | 0,0199 | 0,48 | 0,1844 | 0,91 | 0,3186 | 1,34 | 0,4099 |
| 0,06 | 0,0239 | 0,49 | 0,1879 | 0,92 | 0,3212 | 1,35 | 0,4115 |
| 0,07 | 0,0279 | 0,5 | 0,1915 | 0,93 | 0,3238 | 1,36 | 0,4131 |
| 0,08 | 0,0319 | 0,51 | 0,1950 | 0,94 | 0,3264 | 1,37 | 0,4147 |
| 0,09 | 0,0359 | 0,52 | 0,1985 | 0,95 | 0,3289 | 1,38 | 0,4162 |
| 0,1 | 0,0398 | 0,53 | 0,2019 | 0,96 | 0,3315 | 1,39 | 0,4177 |
| 0,11 | 0,0438 | 0,54 | 0,2054 | 0,97 | 0,3340 | 1,4 | 0,4192 |
| 0,12 | 0,0478 | 0,55 | 0,2088 | 0,98 | 0,3365 | 1,41 | 0,4207 |
| 0,13 | 0,0517 | 0,56 | 0,2123 | 0,99 | 0,3389 | 1,42 | 0,4222 |
| 0,14 | 0,0557 | 0,57 | 0,2157 | 1 | 0,3413 | 1,43 | 0,4236 |
| 0,15 | 0,0596 | 0,58 | 0,2190 | 1,01 | 0,3438 | 1,44 | 0,4251 |
| 0,16 | 0,0636 | 0,59 | 0,2224 | 1,02 | 0,3461 | 1,45 | 0,4265 |
| 0,17 | 0,0675 | 0,6 | 0,2257 | 1,03 | 0,3485 | 1,46 | 0,4279 |
| 0,18 | 0,0714 | 0,61 | 0,2291 | 1,04 | 0,3508 | 1,47 | 0,4292 |
| 0,19 | 0,0753 | 0,62 | 0,2324 | 1,05 | 0,3531 | 1,48 | 0,4306 |
| 0,2 | 0,0793 | 0,63 | 0,2357 | 1,06 | 0,3554 | 1,49 | 0,4319 |
| 0,21 | 0,0832 | 0,64 | 0,2389 | 1,07 | 0,3577 | 1,5 | 0,4332 |
| 0,22 | 0,0871 | 0,65 | 0,2422 | 1,08 | 0,3599 | 1,51 | 0,4345 |
| 0,23 | 0,0910 | 0,66 | 0,2454 | 1,09 | 0,3621 | 1,52 | 0,4357 |
| 0,24 | 0,0948 | 0,67 | 0,2486 | 1,1 | 0,3643 | 1,53 | 0,4370 |
| 0,25 | 0,0987 | 0,68 | 0,2517 | 1,11 | 0,3665 | 1,54 | 0,4382 |
| 0,26 | 0,1026 | 0,69 | 0,2549 | 1,12 | 0,3686 | 1,55 | 0,4394 |
| 0,27 | 0,1064 | 0,7 | 0,2580 | 1,13 | 0,3708 | 1,56 | 0,4406 |
| 0,28 | 0,1103 | 0,71 | 0,2611 | 1,14 | 0,3729 | 1,57 | 0,4418 |
| 0,29 | 0,1141 | 0,72 | 0,2642 | 1,15 | 0,3749 | 1,58 | 0,4429 |
| 0,3 | 0,1179 | 0,73 | 0,2673 | 1,16 | 0,3770 | 1,59 | 0,4441 |
| 0,31 | 0,1217 | 0,74 | 0,2703 | 1,17 | 0,3790 | 1,6 | 0,4452 |
| 0,32 | 0,1255 | 0,75 | 0,2734 | 1,18 | 0,3810 | 1,61 | 0,4463 |
| 0,33 | 0,1293 | 0,76 | 0,2764 | 1,19 | 0,3830 | 1,62 | 0,4474 |
| 0,34 | 0,1331 | 0,77 | 0,2794 | 1,2 | 0,3849 | 1,63 | 0,4484 |
| 0,35 | 0,1368 | 0,78 | 0,2823 | 1,21 | 0,3869 | 1,64 | 0,4495 |
| 0,36 | 0,1406 | 0,79 | 0,2852 | 1,22 | 0,3883 | 1,65 | 0,4505 |
| 0,37 | 0,1443 | 0,8 | 0,2881 | 1,23 | 0,3907 | 1,66 | 0,4515 |
| 0,38 | 0,1480 | 0,81 | 0,2910 | 1,24 | 0,3925 | 1,67 | 0,4525 |
| 0,39 | 0,1517 | 0,82 | 0,2939 | 1,25 | 0,3944 | 1,68 | 0,4535 |
| 0,4 | 0,1554 | 0,83 | 0,2967 | 1,26 | 0,3962 | 1,69 | 0,4545 |
| 0,41 | 0,1591 | 0,84 | 0,2995 | 1,27 | 0,3980 | 1,7 | 0,4554 |
| 0,42 | 0,1628 | 0,85 | 0,3023 | 1,28 | 0,3997 | 1,71 | 0,4564 |
| x | Ф(х) | x | Ф(х) | x | Ф(х) | x | Ф(х) |
| 1,72 | 0,4573 | 1,94 | 0,4738 | 2,32 | 0,4898 | 2,76 | 0,4971 |
| 1,73 | 0,4582 | 1,95 | 0,4744 | 2,34 | 0,4904 | 2,78 | 0,4973 |
| 1,74 | 0,4591 | 1,96 | 0,4750 | 2,36 | 0,4909 | 2,8 | 0,4974 |
| 1,75 | 0,4599 | 1,97 | 0,4756 | 2,38 | 0,4913 | 2,82 | 0,4976 |
| 1,76 | 0,4608 | 1,98 | 0,4761 | 2,4 | 0,4918 | 2,84 | 0,4977 |
| 1,77 | 0,4616 | 1,99 | 0,4767 | 2,42 | 0,4922 | 2,86 | 0,4979 |
| 1,78 | 0,4625 | 2 | 0,4772 | 2,44 | 0,4927 | 2,88 | 0,4980 |
| 1,79 | 0,4633 | 2,02 | 0,4783 | 2,46 | 0,4931 | 2,9 | 0,4981 |
| 1,8 | 0,4641 | 2,04 | 0,4793 | 2,48 | 0,4934 | 2,92 | 0,4982 |
| 1,81 | 0,4649 | 2,06 | 0,4803 | 2,5 | 0,4938 | 2,94 | 0,4984 |
| 1,82 | 0,4656 | 2,08 | 0,4812 | 2,52 | 0,4941 | 2,96 | 0,4985 |
| 1,83 | 0,4664 | 2,1 | 0,4821 | 2,54 | 0,4945 | 2,98 | 0,4986 |
| 1,84 | 0,4671 | 2,12 | 0,4830 | 2,56 | 0,4948 | 3 | 0,49865 |
| 1,85 | 0,4678 | 2,14 | 0,4838 | 2,58 | 0,4951 | 3,2 | 0,49931 |
| 1,86 | 0,4686 | 2,16 | 0,4846 | 2,6 | 0,4953 | 3,4 | 0,49966 |
| 1,87 | 0,4693 | 2,18 | 0,4854 | 2,62 | 0,4956 | 3,6 | 0,499841 |
| 1,88 | 0,4699 | 2,2 | 0,4861 | 2,64 | 0,4959 | 3,8 | 0,499928 |
| 1,89 | 0,4706 | 2,22 | 0,4868 | 2,66 | 0,4961 | 4 | 0,499968 |
| 1,9 | 0,4713 | 2,24 | 0,4875 | 2,68 | 0,4963 | 4,5 | 0,499997 |
| 1,91 | 0,4719 | 2,26 | 0,4881 | 2,7 | 0,4965 | 5 | 0,499999 |
| 1,92 | 0,4726 | 2,28 | 0,4887 | 2,72 | 0,4967 | ||
| 1,93 | 0,4732 | 2,3 | 0,4893 | 2,74 | 0,4969 | ||
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Виды случайных событий
Случайным называется событие, которое при данных условиях может либо произойти, либо не произойти.
Например, событие “при бросании монеты выпал герб” – случайное.
Достоверным называют событие, которое обязательно произойдет в результате опыта.
Невозможным называется событие, которое заведомо не произойдет в условиях опыта.
Достаточно большое число однородных (т.е. происходящих при одних и тех же условиях) случайных событий подчиняется определенным, так называемым вероятностным закономерностям. Установлением этих закономерностей и занимается теория вероятностей.
События называются несовместными, если появление одного из них исключает появление других в одном и том же испытании. В противном случае события совместны.
Несовместные события А1, А2…Аn образуют полнуюгруппу, если в результате опыта обязательно происходит хотя бы одно из них.
Классическое определение вероятности
Вероятность является одним из основных понятий теории вероятностей.
Вероятностью события А называют отношение числа благоприятствующих этому событию исходов (m) к общему числу исходов (n).
Таким образом, вероятность события А определеяется по формуле
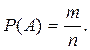
Суммой событий А и В называют событие А+В, состоящее либо в появлении А, либо в появлении В, либо в их совместном появлении.
Произведением событий А и В называют событие АВ, состоящее в совместном появлении этих событий.
Дата: 2019-02-02, просмотров: 1077.
