При решении многих задач оптимальной организации торговли, бытового обслуживания, складского хозяйства и т.п. часто используется интерпретация производственной структуры как системы массового обслуживания (СМО), т.е. системы в которой с одной стороны, постоянно возникают запросы на выполнение каких-либо работ, а с другой стороны происходит постоянное удовлетворение этих запросов.
Каждая СМО состоит из определенного числа обслуживающих единиц, которые будем называть каналами обслуживания. По числу каналов СМО подразделяют на одноканальные и многоканальные.
Предметом теории массового обслуживания является построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность и т.д.) с показателями эффективности СМО:
· абсолютная пропускная способность A – среднее число заявок, обслуживаемых в единицу времени;
· относительная пропускная способность Q – средняя доля пришедших заявок, обслуживаемых системой;
· Pотк – вероятность отказа, т.е. того, что заявка покинет СМО необслуженной;
· 
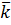- среднее число занятых каналов (для многоканальной системы);
· 
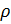- интенсивность нагрузки канала;
· Lсист – среднее число заявок в системе;
· Tсист – среднее время пребывания заявки в системе;
· Lоч – среднее число заявок в очереди (длина очереди);
· Tоч – среднее время пребывания заявки в очереди;
· Pзан – вероятность того, что канал занят (степень загрузки канала);
· Lоб – среднее число заявок, находящихся под обслуживанием и тд.;
СМО делят на два основных типа: СМО с отказами и СМО с ожиданием (очередью). В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ и покидает СМО без дальнейшего участия в процессе обслуживания. СМО с ожиданием подразделяются на разные виды, в зависимости от того, как организована очередь: с ограниченной или неограниченной очередью, с ограниченным временем ожидания и т.п.
Формулы для расчета показателей эффективности работы СМО
СМО с отказами
Одноканальная система:
, 
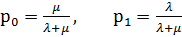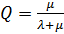
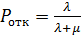
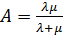
Многоканальная система:
, 
.
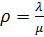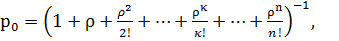
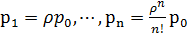
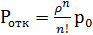
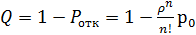
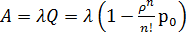
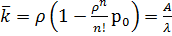3.1.2. СМО с неограниченной очередью:
Одноканальная система:
, 
, 
, 
,
, 
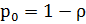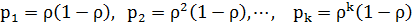
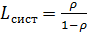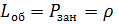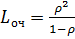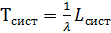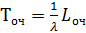
Многоканальная система:
, 
, 
, 
.
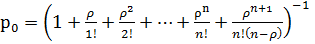
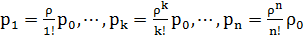
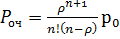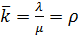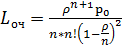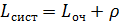3.1.3. СМО с ограниченной очередью:
Одноканальная система:
, 
, 
, 
, 
.
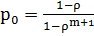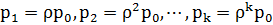
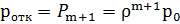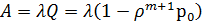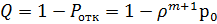
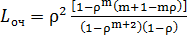
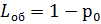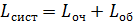Многоканальная система:
,
, 
, 
, 
, 
.
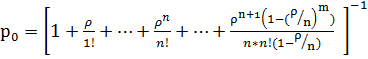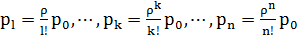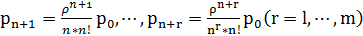
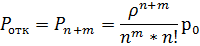
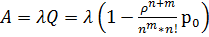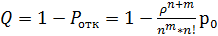
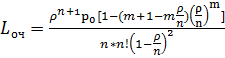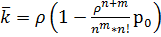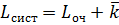Примеры расчета показателей эффективности работы СМО
Пример 1. Магазин посещает в среднем 90 человек в час. Имеющийся один кассир обслуживает в среднем одного покупателя в минуту. Очередь в зал обслуживания ограничена 5 покупателями. Оценить эффективность работы СМО.
Решение:
Система одноканальная с ограниченной очередью.
имеем λ=90 час-1 =1,5 мин-1 , μ=1 мин-1 , ρ=λ/μ=1,5, m=5. Находим р0 и ротк :
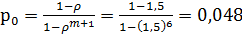
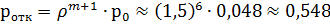т.е. 54,8% покупателей получают отказ в обслуживании.
Среднее число людей, стоящих в очереди:
, .
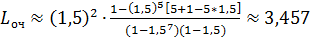
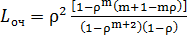
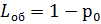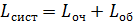Среднее время пребывания в очереди:
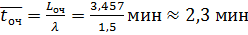
Вывод: необходимо посадить ещё одного кассира, либо уменьшить время обслуживания каждого покупателя.
Пример 2 . На склад в среднем прибывает 3 машины в час. Разгрузку осуществляют 3 бригады грузчиков. Среднее время разгрузки машины - 1час. В очереди в ожидании разгрузки могут находиться не более 4-х машин. Дать оценку работы СМО.
Решение:
Многоканальная система с ограниченной очередью.
Имеем: n = 3, λ = 3 час-1, μ = 1 час-1, ρ = λ/μ = 3, m = 4. Так как ρ = n, то р0 - вероятность отсутствия машин на складе, находим по формуле:
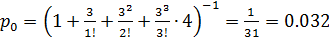
т.е. грузчики работают практически без отдыха.
По формуле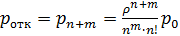 
находим вероятность отказа в обслуживании прибывшей на склад машины:
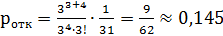
Относительная пропускная способность равна:
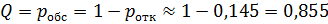
Среднее число машин в очереди:
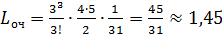машин.
Среднее время пребывания машины на складе:
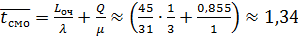часа
Это сравнимо со средним временем разгрузки машины. Можно сделать вывод, что разгрузка машины на складе организована эффективно.
Пример 3 . Небольшое кафе в парке отдыха, одно из многих, имеет 9 столиков. Посетители, увидевшие свободный столик, садятся и их обслуживают. Время пребывания клиентов за столиком в среднем составляет 24 мин.
Если свободных мест нет, люди проходят мимо в расположенные неподалеку практически такие же кафе. Интенсивность потока потенциальных клиентов – 1 человек (пара или группа) за 2 минуты.
Хозяин подумывает немного расширить кафе и довести количество столиков до дюжины. Принесет ли ему выгоду этот шаг, если занятый столик приносит 750 руб в час из которых остается оплатить содержание одного столика - 300 руб/час?
Какое количество столиков принесет ему наибольшую прибыль?
Решение:
Для расчета прибыли от кафе, зависящей, очевидно, от коэффициента загрузки столиков, нужно вычислить характеристики системы массового обслуживания, которую и представляет собой данное кафе.
По условию данной задачи очереди нет совсем. Это соответствует модели СМО с отказами. Видимо предполагается, что столики маленькие и если даже один клиент сидит за ним, к нему никто не подсаживается. Количество каналов равно 9.
Интенсивность входящего потока 30 клиентов в час, т.е. λ=30.
Среднее время обслуживания 24 минуты. Интенсивность потока обслуживания в расчете на часовой интервал времени будет равна μ=2,5 (=60/24) клиентов в час.
Посчитаем прибыль владельца кафе при 9 столиках
, 
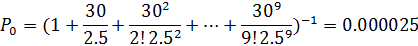
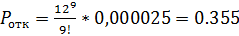
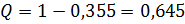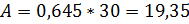
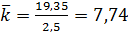
Выручка = 750*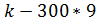 
= 750*7,74-2700=3105
Хозяин платит за столик 300 рублей в час, соответственно за 9 столиков – 2700 рублей в час.
Посчитаем прибыль владельца кафе при 10 столиках
, 
,
, 
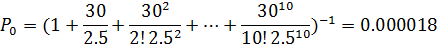
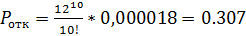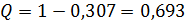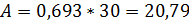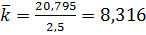
Выручка = 750*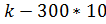 
= 750*8,316-300*10=3237
При 10 столиках он будет получать прибыль в размере 3237 в час.
Посчитаем прибыль владельца кафе при 11 столиках
, 
, 
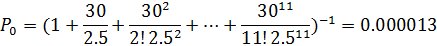
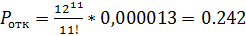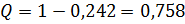
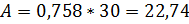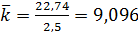
Выручка = 750*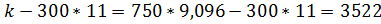 
При 11 столиках он будет получать прибыль в размере 3522 в час.
Посчитаем прибыль владельца кафе при 12 столиках
, 
, 
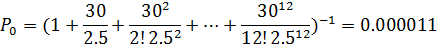
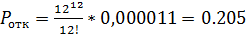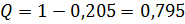
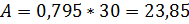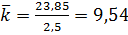
Выручка = 750*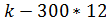 
=750*9,54-300*12=3555
При 12 столиках он будет получать прибыль в размере 3555 в час.
Наш расчет показывает, что если увеличить количество столиков до 12, отдача каждого столика упадет. Но за счет того, что доля потерянных клиентов сильно уменьшится, общая прибыль возрастет.
Таким образом, увеличить количество столиков до 12 - выгодно.
4. Контрольные задания.
Номер контрольного задания определяется традиционно по последней цифре в номере зачетной книжки.
| Номер варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Номера задач | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
Контрольная работа оформляется на листах А4, шрифт Times New Roman 14. Поля: слева – 2,5; справа – 1,5; верхнее и нижнее – по 2 см.
Для защиты контрольной работы иметь электронный вариант.
Дата: 2018-12-28, просмотров: 1518.
