Принятие решений в условии определенности

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ

Методические указания

к выполнению контрольной работы

для студентов направления 38.03.01 «Экономика»

направленности «Финансы и кредит»

заочной формы обучения

Курган 2016

Кафедра: «Торговое дело и логистика»

Дисциплина: «Методы оптимальных решений»

(направление 38.03.01)

Составил: канд. физ.-мат. наук, доцент Лупашко С.Г.

Утверждены на заседании кафедры «1» сентября 2016 г.

Введение

Человеческая деятельность связана с принятием множества решений по способам достижения поставленных целей. При принятии решений приходится учитывать много факторов, в первую очередь, ограниченность ресурсов, неопределенность внешних условий, присутствие конкурирующих сторон.

«Методы оптимальных решений» – это предмет, который изучает математические модели экстремальных (оптимизационных) задач принятия решений. Основным способом моделирования в экономике является метод математи ческого моделирования, который представляет собой описание основных особенностей реального процесса с помощью системы математических формул. Круг развитых к настоящему времени моделей и методов весьма широк. Все они возникли как ответ на непосредственный заказ практического бизнеса, поэтому их распространенность в реальной деловой практике сейчас очень велика.

Принятие решений в условии определенности

Линейное программирование

Методы анализа моделей линейной оптимизации позволяют не просто получить оптимальное решение, но и дают информацию о том, как может изменяться это решение при изменении параметров модели. Именно эта информация, позволяющая получить ответы на вопросы типа “что - если”, представляет особую ценность для лица, принимающего решение.

При постановке любой задачи оптимизации необходимо, прежде всего, определить количественную характеристику цели, которую мы хотим достичь в процессе оптимизации – целевую функцию. Это может быть максимум прибыли или минимум издержек. Целевая функция показывает, почему одно рассматриваемое решение лучше или хуже другого. Целевая функция зависит от величин, называемых переменными решения. Эти величины, мы должны изменять, разыскивая оптимальное решение. Любая оптимизация всегда проводится при наличии некоторых ограничений – условий, ограничивающих изменения переменных решения при поиске максимальной или минимальной целевой функции. Эти ограничения могут диктоваться:

- вторичными целями (например, минимизируя риск инвестиционного портфеля, мы одновременно хотим добиться ожидаемой прибыли не хуже заданной)

- ограниченностью ресурсов, находящихся в нашем распоряжении (денежных, временных, материальных

- установленными «правилами игры» (рыночные ограничения, нормативные акты, лимитирующие ту или иную характеристику или любые требования субъекта, принимающего решения).

Цель оптимизации найти такие значения переменных решения, при которых целевая функция максимальна (или минимальна).

Пример нахождения оптимального решения и его анализ на устойчивость

Большой универсальный магазин собирается заказать новую коллекцию костюмов. Решено заказать 4 модели костюмов. Три модели – это костюмы широкого потребления: (1) костюмы из полиэстера, (2) шерстяные костюмы и (3) костюмы из хлопка. Четвертый тип – это дорогие импортные модельные костюмы. Имеющийся у менеджеров магазина опыт и специальные исследования позволяют оценить средние затраты рабочего времени продавцов на продажу одного костюма каждого типа, затраты на рекламу и площадь в расчете на один костюм каждого типа.

Тип костюма	Прибыль на один костюм	Рабочее время продавцов	Затраты на рекламу	Площадь на один костюм (кв. фут)
Полиэстер	$35	0.4	$2	1.00
Шерсть	$47	0.5	$4	1.50
Хлопок	$30	0.3	$3	1.25
Импорт	$90	1.0	$9	3.00

Магазин предполагает, что сезон будет длиться 90 дней. Магазин открыт 10 часов в день 7 дней в неделю. Предполагается, что 2 продавца постоянно будут в отделе костюмов. Выделенная отделу площадь составляет прямоугольник 100 60 футов. Бюджет, выделенный на рекламу составляет $15000.

a. Сколько костюмов каждого типа нужно закупить для максимизации прибыли?

b . Обоснуйте, будет ли каждое из предлагаемых решений полезно для магазина:

i. Отдать в распоряжение отдела костюмов 400 кв.футов от отдела женской спортивной одежды, предполагается, что на этой площади магазин может получить прибыль $750 за последующие 90 дней;

ii. Истратить дополнительно $400 на рекламу;

iii. Нанять дополнительно продавца на 26 полных дней (все субботы и воскресенья). Это будет стоить магазину $3600 (зарплата, комиссионные).

Решение. Вводим исходные данные в таблицу так, как это показано на рисунке. Следующим шагом определяем переменные. В данной задаче переменными будет количество костюмов каждого типа, которые нужно закупить. Для них создаём новый столбец (он выделен). Никакие данные в этот столбец вводить не нужно, их мы получим в результате поиска решения!

Также необходимо добавить все данные для ограничений. Для удобства расположим их прямо под таблицей.

В ячейке E10 будет ограничение времени. Из условий делаем вывод о том, что работает магазин ежедневно, каждый день 10 часов, поэтому 10 часов умножаем на 90 дней, получаем 900 часов. Но учитываем, что в отделе всегда будет работать 2 продавца, поэтому удваиваем время 900*2=1800 часов. Любая формула начинается со знака «=».

После того, как ввели числа, как на рисунке, и нажали клавишу Enter, компьютер сам совершит расчёт, и в ячейке появится число 1800.

Следующее ограничение по площади. Опять совершаем расчёт: площадь = 100*60 = 6000 футов. Аналогично предыдущему ограничению, вводим это в строку.

Ограничение по рекламе: $15000. Никаких дополнительных вычислений он не требует, поэтому вручную вводим в ячейку F10 число 15000.

Под заданными ограничениями рассчитаем значения реальных расходов, которые получатся у нас при закупке разного количества костюмов. Все они находятся с помощью функции «СУММПРОИЗВ» - сумма произведений.

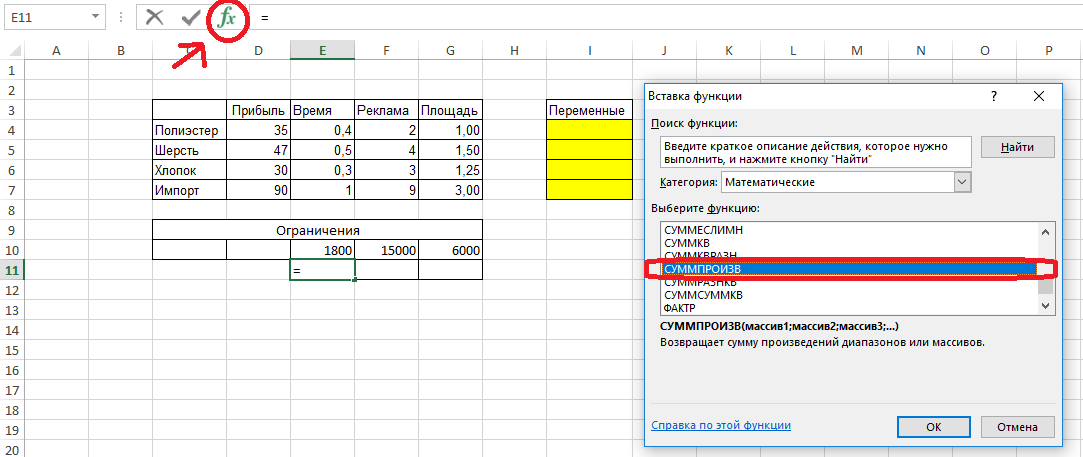
Для расчёта расхода рабочего времени необходимо попарно умножить переменные (ячейки I4:I7) на ячейки расхода времени по продаже 1 костюма (ячейки E4:E7) и сложить эти произведения. Сделаем это с помощью формулы СУММПРОИЗВ. Для этого нажимаем (на рисунке обведена кружочком), появляется окно «Вставка функции». Выбираем категорию «Математические» и среди них ищем СУММПРОИЗВ. В массив 1 помещаем переменные. Массив 2 – расход времени, нажимаем ОК. Компьютер сразу введёт в ячейку готовый результат. Но сейчас этот результат будет 0. Так и должно быть, ведь столбец «переменные» ещё не заполнен. Аналогично вводятся ограничения по рекламе и по площади.

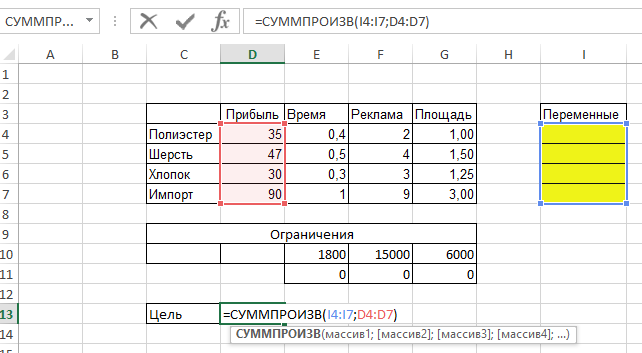
В данной задаче целевая функция будет показывать прибыль, которую получит предприятие. Т.е. нужно умножить переменные на прибыль. Для этого воспользуемся функцией СУММПРОИЗВ. Получаем:

Переходим непосредственно к поиску решения. Он находится на вкладке «Данные» - «Анализ». Нажимаем на «Поиск решения», появляется окно «Параметры поиска решения», с которыми нам предстоит работать.

В первой строке «Оптимизировать целевую функцию» выбираем цель, в нашем случае это ячейка D13. Вторая строка «До», то есть то, к чему стремится функция, выбираем к максимуму.

Изменяя ячейки переменных . В этой строке выбираем все переменные. После этих действий добавляем ограничения с помощью кнопки «Добавить».

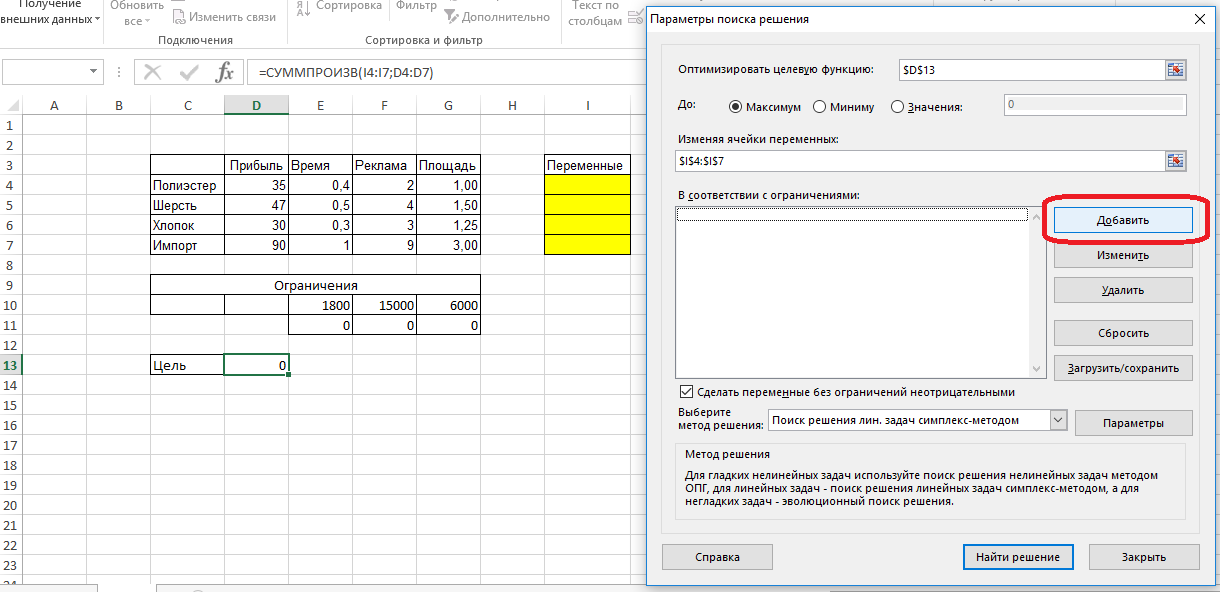
Во-первых, все переменные должны быть не отрицательны (все переменные больше или равны 0). Нажимаем «добавить» и переходим к следующему ограничению. Время, которое мы используем, должно быть не больше, чем имеющийся у нас фонд времени, т.е. ячейка Е11 должна быль меньше или равна ячейки Е10. Вновь нажимаем «Добавить». Аналогично предыдущему добавляем ограничения по рекламе и площади и нажимаем ОК. Получаем:

В методе решения выбираем РЕШЕНИЕ ЛИНЕЙНЫХ ЗАДАЧ СИМПЛЕКСНЫМ МЕТОДОМ.

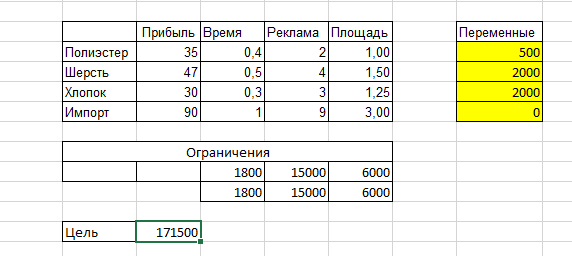
Самое интересное – нажимаем «Найти решение».

Решение найдено. Все ограничения и условия оптимальности выполнены. Нажимаем ОК и смотрим, что же нам предлагает компьютер.

Нам предлагается купить 500 костюмов из полиэстера, 2000 костюмов из шерсти, 2000 костюмов из хлопка и совсем не покупать импортные костюмы, и в таком случае мы должны будем получить прибыль в размере 171500 $.

Для ответа на вопросы b необходимо создать «Отчет об устойчивости». Мы вновь заходим в окно «Поиск решения», нажимаем «Найти решение» и в колонке «отчёты» выбираем «устойчивость».

Кликаем ОК. Теперь на новом листе появился отчёт об устойчивости, в котором можно найти много информации, касающейся переменных и ограничений.

Ячейки переменных

Окончат.

Приведен.

Целев.функ.

Допустим.

Допустимое

Яч-ка

Имя

Значение

Стоимость

Коэффиц.

Увеличен.

Уменьшен.

$I$4

Полиэстер

500

1,57

$I$5

Шерсть

2000

0,5

1,375

$I$6

Хлопок

2000

2,75

0,5

$I$7

Импорт

-5,83

5,83

1E+30

Ограничения

Окончат.

Теневая

Ограничение

Допустимое

Яч-ка

Имя

Значение

Цена

Прав. стор.

Увеличен.

Уменьшен.

$E$11

Время

1800

73,33

1800

300

150

$F$11

15000

1,83

15000

428,57

1500

$G$11

Площадь

6000

500

250

Первая таблица содержит данные о переменных. Если продукт (в данной задаче это определенный тип костюма) входит в оптимальный план, то его приведённая стоимость равна 0. Если же продукт не входит в оптимальный план, то его приведённая стоимость отрицательна. Это значит, что если мы хотим, чтобы продукт вошёл в оптимальный план, то нужно увеличить целевой коэффициент на эту величину.

Вторая таблица содержит всю информацию по ограничениям. Окончательное значение содержит величину левой части ограничений. В нашем случае это реальный расход ресурсов.

Теневая цена никак не соотносится с рыночной и представляет величину изменения целевой функции при изменении правой части ограничений на единицу. В нашем случае – это ценность ресурса для производителя. Она показывает, насколько изменится целевая функция при изменении запаса ресурса на единицу. Например, если площадь увеличится на 1 кв. фут, то целевая функция увеличится на 2.

ВАЖНО! Если мы меняем целевые коэффициенты или правую сторону ограничений в пределах их интервалов устойчивости, то целевая функция меняется, а оптимальное решение остается неизменным. В СЛУЧАЕ ЕСЛИ МЫ ВЫХОДИМ ЗА ПРЕДЕЛЫ ИНТЕРВАЛА УСТОЙЧИВОСТИ, МЕНЯЕТСЯ ВСЁ!

i. Согласно условию, в распоряжение отдела костюмов могут выделить площадь 400кв. футов.

Поскольку увеличение площади будет в пределах интервала устойчивости, для расчета увеличения прибыли воспользуемся значением Теневой Цены. 400*2=800.

Но по условиям сказано, что если эта площадь останется за отделом женской спортивной одежды, то ожидаемая прибыль составит 750 у.е. за последующие 90 дней. Итого: 800-750=50. В данном случае, прибыль увеличивается незначительно, поэтому, стоит ли отдавать данные площади, будет решать руководитель предприятия.

Так же как и в предыдущем пункте, увеличение расходов на рекламу будет в пределах интервала устойчивости. Увеличение целевой функции составит: 400*1,83= 732 у.е.

Обратив внимание на теневую цену, можно смело сказать, что и увеличение расходов на рекламу и увеличение площади отдела не играет особо важной роли, более эффективно будет изменять такой ресурс, как время.

Дополнительное время составит 260 часов (в пределах интервала устойчивости). Это позволит увеличить доход на 260*73,33=19065,8 у.е. Но из этой величины необходимо вычесть 3600 у.е. - зарплата и комиссионные. Увеличение целевой функции составит: 19065,8-3600=15465,8 у.е.

Игры с природой

К играм с природой относятся ситуации, в которых второй игрок принимает решение о выборе своей стратегии неосознанно, случайным образом.

Собираясь в туристический поход, мы укладываем вещи в рюкзак с учетом неизвестной погоды и преследуем цель получить максимум удовольствий, не превращаясь в рекордсмена по переноске тяжестей. Создавая систему профилактических и аварийных ремонтов, мы преследуем цель, не зная в точности времени возникновения аварий.

Пример выбора оптимальной стратегии

Планируется выпуск новой продукции, для чего необходимо закупить станки. Система оптовой торговли может поставить не более 50 станков; комплект поставки - 10 станков. Минимальный объем поставок - 20 станков. Соответственно, вектор решений об объеме поставок X = (20,30,40,50).

Ежегодный доход от продукции, снимаемой с одного станка, cоставляет 21.9 тыс.руб. Оптовая цена одного станка 4.775 тыс.руб., эксплуатационные расходы - 3.6 тыс. руб. Затраты на подготовку производства составляют 25.5 тыс.руб. и не зависят от числа станков и объема выпуска.

Решение. Пусть спрос пропорционален количеству продукции, снимаемой с S работающих станков, вектор состояния спроса S = (0,10,20,30,40,50).

Элементы платежной матрицы:

W_ij = (21.9 - 3.6) * min( X_i, S_j) - 4.775 X_i - 25.5


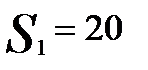
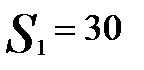
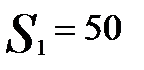
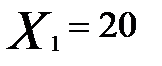
-121	62	245	245	245	245
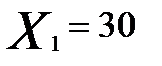
-168,75	14,25	197,25	280,25	380,35	380,25
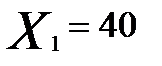
-216,5	-33,5	149,5	332,5	515,5	515,5
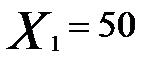
-264,25	-81,25	101,75	284,75	467,75	650,75

Например,

W₁₁ = -(4.775 20+25.5) = -121,
W₁₂ = (21.9-3.6) * 10-(4.775 20+25.5) = 62,
W₁₃ = (21.9-3.6) * 20-(4.775 20+25.5) = 245,
W₁₄ = W₁₅ = 245 (спрос останется неудовлетворенным).

Предположим, что в нашем распоряжении имеются статистические данные, позволяющие оценить вероятность того или иного спроса, и этот опыт может быть использован для оценки будущего. При известных вероятностях P_j для спроса S_j можно найти математическое ожидание W(X,S,P) и определить вектор X^*, дающий

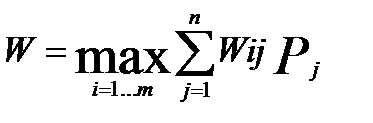
Если для вышеприведенного примера задать вектор P = (0.01, 0.09, 0.2, 0.3, 0.3, 0.1), то математические ожидания прибыли при разных выборах:

W₁ =-121*0.01 + 62*0.09 + 245*0.2 + 245*0.3 + 245*0.3 + 245*0.1 = 224.87,

W₂ = 305.22, W₃ = 330.675, W₄ = 301.12

и выбор максимального значения обнаруживает оптимальность варианта 40 станков с ожидаемой прибылью 330.675 тыс.руб.

Критерий Лапласа

Если нет достаточных оснований считать, что вероятности того или иного спроса имеют неравномерное распределение, то они принимаются одинаковыми и задача сводится к поиску варианта, дающего

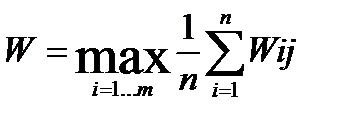
Для нашего примера

W₁ = (-121 + 62 + 245 + 245 + 245 + 245)/6 = 153.5,
W₂ = 197.25, W₃ =210.5, W₄ = 193.5

и выбор максимального значения обнаруживает оптимальность выбора варианта 40 станков с ожидаемой прибылью 210.5 тыс.руб.

Критерий Вальда

Критерий Вальда обеспечивает выбор осторожной, пессимистической стратегии. Для каждого решения X_i выбирается самая худшая ситуация (наименьшее из W_ij) и среди них отыскивается гарантированный максимальный эффект.

В нашем примере W = max(-121, -168.75, -216.5, -264.25) = -121, т.е. по этому критерию следует закупить 20 станков и максимальный возможный убыток не превысит 121 тыс.руб.

Критерий Гурвица

Критерий Гурвица предлагает некоторый компромисс:

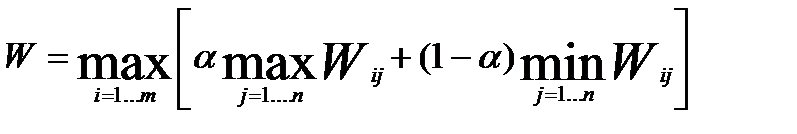, где параметр α принимает значение от 0 до 1 и выступает как коэффициент оптимизма. Так в нашем примере значения W рассчитаны для различных α:


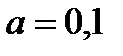
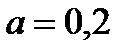
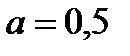
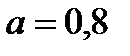
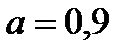
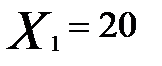
-84,4	-47,0	62	171	206,4
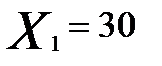
-113,85	-58,95	105,75	270,45	325,35
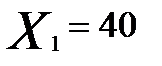
-140,4	-70,1	149,5	369,1	442,3
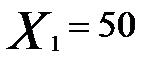
-172,75	-81,25	193,25	467,75	559,25

При α=0.5 (равновероятных шансах на успех и неудачу) следует закупить 50 станков и ожидать прибыль порядка 193.25 тыс. руб.

При вероятности успеха 0.2 не следует закупать более 20 станков с надеждой, что убытки не превысят 47 тыс.руб.

Критерий Сэвиджа

Суть этого критерия заключается в нахождении минимального риска. При выборе решения по этому критерию сначала матрице функции полезности (эффективности) сопоставляется матрица сожалений:

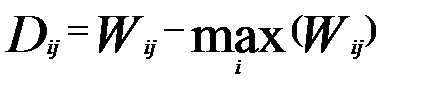
элементы которой отражают выгоду, упущенную в результате принятия i-го решения в j-м состоянии. Затем по матрице D выбирается решение по пессимистическому критерию Вальда, дающее наименьшее значение максимального сожаления.

Для нашего примера отыскиваем матрицу D, вычитая (-121) из первого столбца матрицы полезности, 62 из второго и т.д.


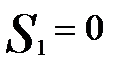
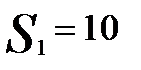
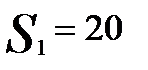
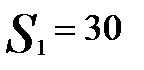
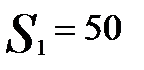
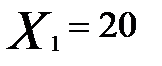
0	0	0	-135,25	-270,5	-405,75
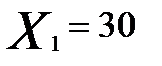
-47,75	-47,75	-47,75	0	-135,25	-270,5
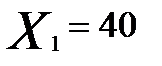
-95,5	-95,5	-95,5	-47,75	0	-135,25
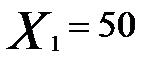
-143,25	-143,25	-143,25	-95,5	-47,75	0

Наибольшее значение среди минимальных элементов строк здесь равно max[-405.75, -270.5, -135.25, -143.25]=-135.25 и, покупая 40 станков, мы уверены, что в худшем случае убытки не превысят 135.25 тыс.руб.

Выбор критерия нахождения оптимального решения осуществляется с учетом имеющейся информации о втором игроке и реальной ситуации.

Различные критерии приводят к различным выводам:

Возможность выбора критерия дает свободу лицам, принимающим экономические решения, при условии, что они располагают достаточными средствами для постановки подобной задачи.

СМО с отказами

Одноканальная система:

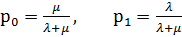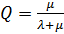
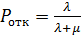
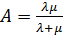
Многоканальная система:

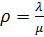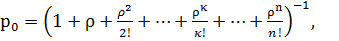
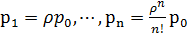
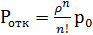
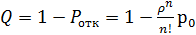
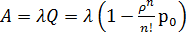
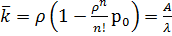3.1.2. СМО с неограниченной очередью:

Одноканальная система:

, , ,

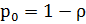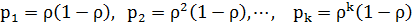
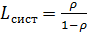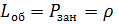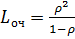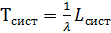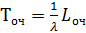
Многоканальная система:

, , , .

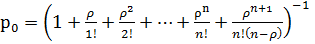
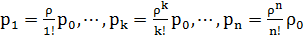
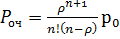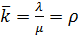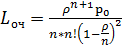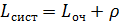3.1.3. СМО с ограниченной очередью:

Одноканальная система:

, ,

, .

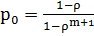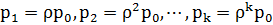
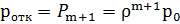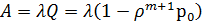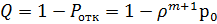
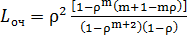
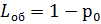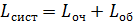Многоканальная система:

, , .

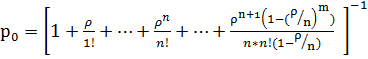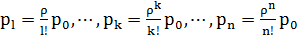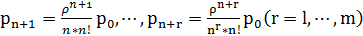
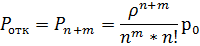
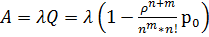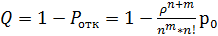
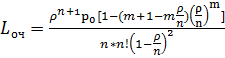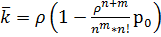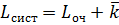Примеры расчета показателей эффективности работы СМО

Пример 1. Магазин посещает в среднем 90 человек в час. Имеющийся один кассир обслуживает в среднем одного покупателя в минуту. Очередь в зал обслуживания ограничена 5 покупателями. Оценить эффективность работы СМО.

Решение:

Система одноканальная с ограниченной очередью.

имеем λ=90 час^-1=1,5 мин^-1, μ=1 мин^-1, ρ=λ/μ=1,5, m=5. Находим р₀и р_отк:

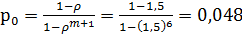
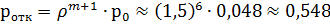т.е. 54,8% покупателей получают отказ в обслуживании.

Среднее число людей, стоящих в очереди:

, .

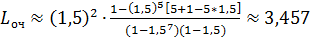
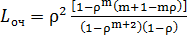
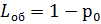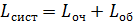Среднее время пребывания в очереди:

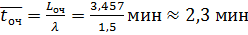
Вывод: необходимо посадить ещё одного кассира, либо уменьшить время обслуживания каждого покупателя.

Пример 2 . На склад в среднем прибывает 3 машины в час. Разгрузку осуществляют 3 бригады грузчиков. Среднее время разгрузки машины - 1час. В очереди в ожидании разгрузки могут находиться не более 4-х машин. Дать оценку работы СМО.

Решение:

Многоканальная система с ограниченной очередью.

Имеем: n = 3, λ = 3 час-1, μ = 1 час-1, ρ = λ/μ = 3, m = 4. Так как ρ = n, то р₀ - вероятность отсутствия машин на складе, находим по формуле:

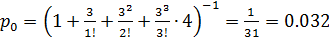
т.е. грузчики работают практически без отдыха.

По формуле 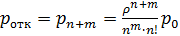находим вероятность отказа в обслуживании прибывшей на склад машины:

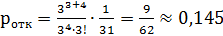
Относительная пропускная способность равна:

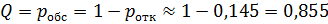
Среднее число машин в очереди:

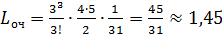машин.

Среднее время пребывания машины на складе:

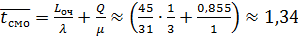часа

Это сравнимо со средним временем разгрузки машины. Можно сделать вывод, что разгрузка машины на складе организована эффективно.

Пример 3 . Небольшое кафе в парке отдыха, одно из многих, имеет 9 столиков. Посетители, увидевшие свободный столик, садятся и их обслуживают. Время пребывания клиентов за столиком в среднем составляет 24 мин.

Если свободных мест нет, люди проходят мимо в расположенные неподалеку практически такие же кафе. Интенсивность потока потенциальных клиентов – 1 человек (пара или группа) за 2 минуты.

Хозяин подумывает немного расширить кафе и довести количество столиков до дюжины. Принесет ли ему выгоду этот шаг, если занятый столик приносит 750 руб в час из которых остается оплатить содержание одного столика - 300 руб/час?

Какое количество столиков принесет ему наибольшую прибыль?

Решение:

Для расчета прибыли от кафе, зависящей, очевидно, от коэффициента загрузки столиков, нужно вычислить характеристики системы массового обслуживания, которую и представляет собой данное кафе.

По условию данной задачи очереди нет совсем. Это соответствует модели СМО с отказами. Видимо предполагается, что столики маленькие и если даже один клиент сидит за ним, к нему никто не подсаживается. Количество каналов равно 9.

Интенсивность входящего потока 30 клиентов в час, т.е. λ=30.

Среднее время обслуживания 24 минуты. Интенсивность потока обслуживания в расчете на часовой интервал времени будет равна μ=2,5 (=60/24) клиентов в час.

Посчитаем прибыль владельца кафе при 9 столиках

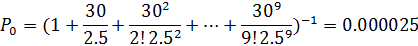
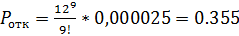
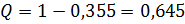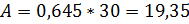
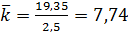
Выручка = 750* 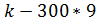= 750*7,74-2700=3105

Хозяин платит за столик 300 рублей в час, соответственно за 9 столиков – 2700 рублей в час.

Посчитаем прибыль владельца кафе при 10 столиках

, ,

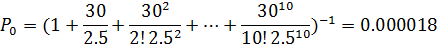
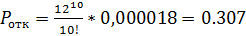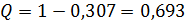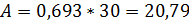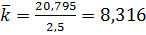
Выручка = 750* 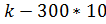= 750*8,316-300*10=3237

При 10 столиках он будет получать прибыль в размере 3237 в час.

Посчитаем прибыль владельца кафе при 11 столиках

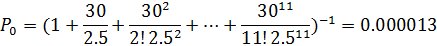
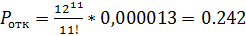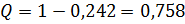
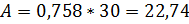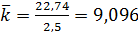
Выручка = 750*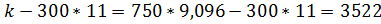

При 11 столиках он будет получать прибыль в размере 3522 в час.

Посчитаем прибыль владельца кафе при 12 столиках

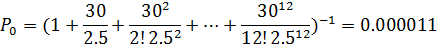
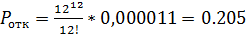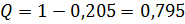
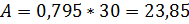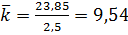
Выручка = 750* 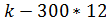=750*9,54-300*12=3555

При 12 столиках он будет получать прибыль в размере 3555 в час.

Наш расчет показывает, что если увеличить количество столиков до 12, отдача каждого столика упадет. Но за счет того, что доля потерянных клиентов сильно уменьшится, общая прибыль возрастет.

Таким образом, увеличить количество столиков до 12 - выгодно.

4. Контрольные задания.

Номер контрольного задания определяется традиционно по последней цифре в номере зачетной книжки.

Номер варианта	1	2	3	4	5	6	7	8	9	10
Номера задач	1	2	3	4	5	6	7	8	9	10
	11	12	13	14	15	16	17	18	19	20
	21	22	23	24	25	26	27	28	29	30

Контрольная работа оформляется на листах А4, шрифт Times New Roman 14. Поля: слева – 2,5; справа – 1,5; верхнее и нижнее – по 2 см.

Для защиты контрольной работы иметь электронный вариант.

Тема «Теория игр»

ЗАДАЧА 11. Производитель аэросаней должен сделать заказ на двигатели на месяц за два месяца вперед. Кампания делает сани на заказ и количество произведенной продукции определяется числом заказов на сани на следующий месяц. Число заказов неизвестно, но предыдущий опыт позволяет оценить вероятность различных уровней спроса. Данные представлены в таблице.

Кол-во двигателей	500	750	1000	1250	1500	1750
Вероятность продаж	0,15	0,25	0,25	0,2	0,1	0,05

Если купленный двигатель используется в тот месяц, для которого он куплен, он дает прибыль $250, если он залеживается до следующего месяца, это влечет убытки $50.

a. Постройте матрицу прибылей и затрат. Каков оптимальный размер заказа? Какова цена совершенной информации?

b. Используйте критерии максимина, минимаксного риска для принятия решения о величине заказа.

c. Как изменится оптимальное решение, если потери от неиспользованного вовремя, двигателя составляют $200? Как изменится стоимость совершенной информации?

ЗАДАЧА 12. Менеджер оптового склада хозяйственных товаров должен решить, сколько газонокосилок заказать для наступающего сезона. Каждая газонокосилка, проданная в сезон, дает $100 прибыли, а каждая непроданная – приносит убытка на $150. Менеджер может разместить заказ только на целое число сотен косилок. И продавать их дилерам собирается по сотням. Вероятности различных значений спроса, которые определяются имеющимися у менеджера статистическими данными, представлены в таблице.

Спрос	100	200	300	400	500	600	700
Вероятности	0,03	0,08	0,17	0,27	0,3	0,11	0,04

a. Постройте таблицы выигрышей-потерь. Используйте различные критерии для нахождения оптимального решения о величине заказа. Какой критерий Вы предпочли бы в этой ситуации? Почему?

b. Маркетинговое агентство предлагает провести специальное исследование для уточнения спроса на данный вид товара в наступающем сезоне. Стоимость исследования $8000.Стоит ли менеджеру воспользоваться услугами агентства? Почему?

ЗАДАЧА 13. Менеджер закупочного отдела магазина хозяйственных товаров должен решить сколько циркулярных пил закупить для продажи в текущем строительном сезоне. Каждая пила покупается у дилера за $60, а продается в магазине за $100. Каждая непроданная в сезон пила требует серьезных расходов на хранение и в результате приносит убыток $25.

Менеджер может покупать товар у дилера только партиями по 100 штук. Из прошлого опыта известны вероятности продать партии товара различного размера:

Спрос	300	400	500	600	700
Вероятности	0,1	0,2	0,3	0,25	0,15

a. Сформируйте матрицу прибылей (выигрышей) и матрицу упущенных возможностей (рисков). Используйте различные критерии для принятия решения о величине заказа циркулярных пил. Какова будет средняя прибыль при каждом из выборов партии? Какой критерий Вы предпочитаете в данной ситуации? Объясните.

b. Независимая служба маркетинговых исследований предлагает сделать прогноз спроса на пилы в районе данного магазина на наступающий сезон. Стоимость исследования $3100. Воспользовались ли бы Вы таким предложением, будь Вы на месте менеджера закупочного отдела? Ответ обоснуйте.

ЗАДАЧА 14. Годовой запас ботинок некоторого популярного типа для большого универмага нужно заказывать заранее. Каждая пара стоит $ 30, продается за $ 60, и может быть продана на распродаже только за $ 15, если не будет продана до конца года. Рассматриваются следующие варианты заказа: 20, 30, 40, или 50 пар.

Уровни спроса и их вероятности даны в таблице:

Спрос	20	25	30	35	40	45	50
Вероятность	0,20	0,25	0,20	0,15	0,10	0,05	0,05

a. Сформируйте матрицу прибылей (выигрышей) и матрицу упущенных возможностей (рисков). Сколько пар ботинок нужно заказывать, чтобы максимизировать ожидаемую прибыль?

b. Используйте различные критерии для принятия решения о величине заказа. Какой критерий Вы предпочитаете в данной ситуации? Объясните.

ЗАДАЧА 15. Зеленщица на маленьком рынке в провинциальном городке продает зелень, выращенную в собственной отапливаемой теплице. Свежесрезанная зелень продается в тот же день за 3 рубля. Если часть зелени не продается, ее приходится выбрасывать и зеленщица теряет на этом в среднем по 2 руб за пучок, (издержки по содержанию теплицы). Хозяйка каждый день записывает, сколько десятков пучков зелени ей удалось продать. Записи за последние 3 или 4 месяца можно было бы обобщить следующим образом: 1 день удалось продать только 4 десятка пучков зелени, 4 дня - 5 дес. пучков, 15 дней – 6 дес., 25 – 7 дес., 30 – 8, 23 – 9, 9 – 10, 4 – 11 и 1 день – 12 дес. пучков.

a. Подскажите хозяйке, какое количество пучков зелени нужно срезать к торговому дню, чтобы максимизировать прибыль?

b. Соседка зеленщицы - гадалка, иногда предсказывает ей какое количество зелени нужно приготовить к следующему дню. Гадалка предлагает за 5 рублей за сеанс каждый вечер предсказывать спрос на завтра. Стоит ли зеленщице тратиться на гадалку?

c. Используйте различные критерии принятия решения о количестве подготавливаемой зелени.

ЗАДАЧА 16. Маленькая кондитерская в курортном городе продает выпечку собственного производства. Фирменные торты выпекаются каждое утро и продаются по цене $7 (при себестоимости - $3). Если торт не продается в день изготовления, он выбрасывается. Записи, которые ведет хозяйка, показывают, что за последние 100 дней спрос на эти торты имел следующее распределение.

Кол-во проданных тортов	8	9	10	11	12
Кол-во дней	15	25	30	20	10

a. Подскажите хозяйке, какое количество тортов нужно выпекать, чтобы максимизировать прибыль?

b. Хозяйка водит дружбу с гадалкой, которая каждый вечер предсказывает ей какое количество тортов нужно выпекать на следующий день и берет за услугу $2. Стоит ли хозяйке тратиться на гадалку?

c. Используйте различные критерии для принятия решения о партии тортов.

ЗАДАЧА 17. Фирма Тракторы и СХ Орудия Барни продает малые трактора владельцам окрестных ферм. Дилер должен решить, сколько тракторов заказать у производителя зимой, когда цены наиболее низкие, чтобы обеспечить продажи в течение. Базируясь на исторических данных, дилер полагает, что распределение вероятностей спроса, связанное с количеством проданных тракторов, следующее:

Количество тракторов, шт	5-14	15-19	20-24	25-29	30-33	35-40
Вероятность спроса	0,1	0,25	0,35	0,2	0,05	0,05

Прибыль дилеру от продажи одного трактора 5000 $, а потеря, связанная с необходимостью хранить трактор до следующего сезона 2000 $. Дилер может заказывать любое количество тракторов.

a. Каков оптимальный размер партии? Какой критерий Вы использовали бы, если дилер собирается запасать известную марку трактора?

b. Вообразите, что дилер хотел бы переключится на новую, практически неизвестную потребителю, марку трактора. Какой размер партии Вы рекомендовали бы в этом случае?

c. Местное маркетинговое агентство предлагает делать специальное рыночное исследование относительно спроса на тракторы на следующий сезон и просит о 6000$. Вы купите его услуги?

ЗАДАЧА 18. Компания «Супермаски» продает маски Halloween в киосках в местном парке. Магазинчики открыты в течение октября месяца. Маски стоят магазину $ 3.45 каждая; они продаются в розницу по $9.95. Любая маска, не купленная вовремя, после праздника продается специалисту по распродаже товаров по цене $1.80.

Результаты продаж за последние 3 года в 10 киосках компании сведены в таблицу.

Средние продажи	750	800	850	900	950	1000	1050	1100
Случаев	1	4	9	6	4	3	2	1

Поскольку маски импортированы из Азии, заказ должен быть размещен в мае, последующее изменение заказа невозможно.

a. Постройте таблицу выигрышей и потерь. Подсчитайте вероятности различных уровней спроса.

b. Какой заказ (в расчете на 1 киоск) максимизирует среднюю ожидаемую прибыль?

c. Какова будет прибыль, если стоимость арендной платы, труда, страхования и прочие издержки по использованию киоска - приблизительно $ 3000 за сезон продаж?

Задача 19. Компьютерная школа проводит курсы по подготовке специалистов по обслуживанию компьютерных сетей. Школа гарантирует трудоустройство каждому слушателю, успешно закончившему курсы в течении недели. В противном случае школа возвращает слушателю всю стоимость обучения ($2000). С каждого трудоустроенного выпускника школа имеет прибыль - $1000. Из предыдущего опыта и из анализа объявлений о приглашении на работу квалифицированных специалистов по компьютерным сетям менеджер школы оценил вероятность трудоустройства подготовленных специалистов для типичной недели.

Спрос	10	11	12	13	14	15
Вероятность	0,1	0,2	0,25	0,25	0,15	0,05

a. Сформируйте матрицу прибылей (выигрышей) и матрицу упущенных возможностей (рисков). Какой величины класс нужно формировать школе, чтобы максимизировать прибыль? Какова будет средняя прибыль при оптимальном размере класса?

b. Используйте различные критерии для принятия решения о величине класса.

c. Независимая служба маркетинговых исследований предлагает сделать прогноз спроса на специалистов, выпускаемых школой. Стоимость исследования $1300. Воспользовались ли бы Вы таким предложением, будь Вы на месте менеджера школы. Ответ обоснуйте количественно.

ЗАДАЧА 20. Менеджер оптовой базы должен решить, сколько вагонов упаковочных ящиков заказать для наступающего сезона сбора мандаринов. Каждый вагон, проданный в сезон, дает $1200 прибыли, а каждый непроданный приносит убытка на $1000, вследствие замораживания капитала, расходов на хранение, потерь вследствие небрежного хранения и проч.

Кол-во необходимой тары	1	2	3	4	5	6	7	8	9	10	11
Вероятности	0,01	0,02	0,03	0,05	0,07	0,1	0,14	0,17	0,21	0,17	0,03

Вероятности различных значений спроса, которые определяются имеющимися у менеджера статистическими данными по урожаям за многие годы, представлены в таблице.

a. Постройте таблицы выигрышей-потерь. Используйте критерий максимина, минимаксного риска и EMV о величине заказа. Какой критерий Вы предпочли бы в этой ситуации? Почему?

b. Аналитическая служба местной администрации предлагает провести специальное исследование для оценки ожидающегося урожая в наступающем сезоне. Какую предельную сумму менеджер может платить за такие ежегодные исследования.

МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ

Методические указания

к выполнению контрольной работы

для студентов направления 38.03.01 «Экономика»

направленности «Финансы и кредит»

заочной формы обучения

Курган 2016

Кафедра: «Торговое дело и логистика»

Дисциплина: «Методы оптимальных решений»

(направление 38.03.01)

Составил: канд. физ.-мат. наук, доцент Лупашко С.Г.

Утверждены на заседании кафедры «1» сентября 2016 г.

Введение

Принятие решений в условии определенности

Линейное программирование

- ограниченностью ресурсов, находящихся в нашем распоряжении (денежных, временных, материальных

Пример нахождения оптимального решения и его анализ на устойчивость

Тип костюма	Прибыль на один костюм	Рабочее время продавцов	Затраты на рекламу	Площадь на один костюм (кв. фут)
Полиэстер	$35	0.4	$2	1.00
Шерсть	$47	0.5	$4	1.50
Хлопок	$30	0.3	$3	1.25
Импорт	$90	1.0	$9	3.00

a. Сколько костюмов каждого типа нужно закупить для максимизации прибыли?

b . Обоснуйте, будет ли каждое из предлагаемых решений полезно для магазина:

ii. Истратить дополнительно $400 на рекламу;

Также необходимо добавить все данные для ограничений. Для удобства расположим их прямо под таблицей.

В методе решения выбираем РЕШЕНИЕ ЛИНЕЙНЫХ ЗАДАЧ СИМПЛЕКСНЫМ МЕТОДОМ.

Самое интересное – нажимаем «Найти решение».

Ячейки переменных

Окончат.

Приведен.

Целев.функ.

Допустим.

Допустимое

Яч-ка

Имя

Значение

Стоимость

Коэффиц.

Увеличен.

Уменьшен.

$I$4

Полиэстер

500

1,57

$I$5

Шерсть

2000

0,5

1,375

$I$6

Хлопок

2000

2,75

0,5

$I$7

Импорт

-5,83

5,83

1E+30

Ограничения

Окончат.

Теневая

Ограничение

Допустимое

Яч-ка

Имя

Значение

Цена

Прав. стор.

Увеличен.

Уменьшен.

$E$11

Время

1800

73,33

1800

300

150

$F$11

15000

1,83

15000

428,57

1500

$G$11

Площадь

6000

500

250

i. Согласно условию, в распоряжение отдела костюмов могут выделить площадь 400кв. футов.

Дата: 2018-12-28, просмотров: 1426.

12 3 4 5 Следующая ⇒