Количественные методы выбора наилучших альтернатив в условиях неопределенности и риска, методы теории игр часто могут служить хорошей основой для выработки стратегии компании в условиях быстро меняющейся окружающей среды.

Поиск оптимального решения в антогонистических играх

Интересы участников игры (игроков) могут оказаться несовпадающими и даже противоположными. В последнем случае игра называется антагонистической.

Система правил, однозначно определяющая выбор хода игрока в зависимости от сложившейся ситуации, называется стратегией.

Каждая фиксированная стратегия игрока, где любой ситуации сопоставлен конкретный выбор, называется чистой. В реальности чаще используются т.н. смешанные стратегии, где чистые стратегии смешиваются с некоторыми вероятностями.

Простейшими являются игры 2 лиц с нулевой суммой.

Пусть в такой игре игрок 1 имеет m выборов и игрок 2 - n выборов. Если игрок 1 делает свой i-й выбор, а игрок 2-свой j-й выбор, то выигрыш игрока 1 (проигрыш игрока 2) равен Rij. Такая игра называется матричной и матрица R = [ R_ij/ i=1..m , j=1..n ] называется матрицей выигрышей (платежной матрицей).

При ведении игры игрок должен ориентироваться на оптимальную политику партнера и наказывать его за отступления от таковой. Проведем рассуждения за игрока 1. Если Я воспользуюсь i-м выбором, мой противник для минимизации моего выигрыша сделает тот из своих выборов, который даст min R_ij. Соответственно, Я должен использовать тот выбор, который гарантирует мне выигрыш, не меньший

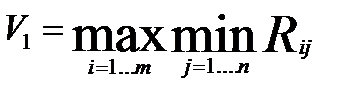
Противник, рассуждая аналогично, приходит к выводу о гарантированном проигрыше.

Если в матрице выигрышей существует элемент R_kl= V₁= V₂, то говорят о наличии оптимальной политики "в пространстве чистых стратегий" и оптимальными выборами для игроков соответственно являются выборы k и l. Пару (k, l) называют седловой точкой.

Если седловой точки нет – решение находится в смешанных стратегиях.

Игры с природой

К играм с природой относятся ситуации, в которых второй игрок принимает решение о выборе своей стратегии неосознанно, случайным образом.

Собираясь в туристический поход, мы укладываем вещи в рюкзак с учетом неизвестной погоды и преследуем цель получить максимум удовольствий, не превращаясь в рекордсмена по переноске тяжестей. Создавая систему профилактических и аварийных ремонтов, мы преследуем цель, не зная в точности времени возникновения аварий.

Пример выбора оптимальной стратегии

Планируется выпуск новой продукции, для чего необходимо закупить станки. Система оптовой торговли может поставить не более 50 станков; комплект поставки - 10 станков. Минимальный объем поставок - 20 станков. Соответственно, вектор решений об объеме поставок X = (20,30,40,50).

Ежегодный доход от продукции, снимаемой с одного станка, cоставляет 21.9 тыс.руб. Оптовая цена одного станка 4.775 тыс.руб., эксплуатационные расходы - 3.6 тыс. руб. Затраты на подготовку производства составляют 25.5 тыс.руб. и не зависят от числа станков и объема выпуска.

Решение. Пусть спрос пропорционален количеству продукции, снимаемой с S работающих станков, вектор состояния спроса S = (0,10,20,30,40,50).

Элементы платежной матрицы:

W_ij = (21.9 - 3.6) * min( X_i, S_j) - 4.775 X_i - 25.5

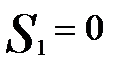
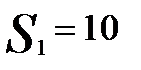
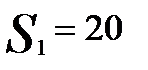
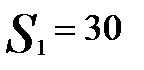
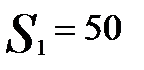
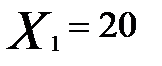
	-121	62	245	245	245	245
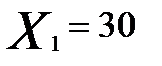
	-168,75	14,25	197,25	280,25	380,35	380,25
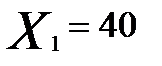
	-216,5	-33,5	149,5	332,5	515,5	515,5
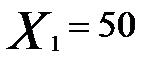
	-264,25	-81,25	101,75	284,75	467,75	650,75

Например,

W₁₁ = -(4.775 20+25.5) = -121,
W₁₂ = (21.9-3.6) * 10-(4.775 20+25.5) = 62,
W₁₃ = (21.9-3.6) * 20-(4.775 20+25.5) = 245,
W₁₄ = W₁₅ = 245 (спрос останется неудовлетворенным).

Предположим, что в нашем распоряжении имеются статистические данные, позволяющие оценить вероятность того или иного спроса, и этот опыт может быть использован для оценки будущего. При известных вероятностях P_j для спроса S_j можно найти математическое ожидание W(X,S,P) и определить вектор X^*, дающий

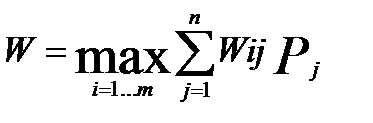
Если для вышеприведенного примера задать вектор P = (0.01, 0.09, 0.2, 0.3, 0.3, 0.1), то математические ожидания прибыли при разных выборах:

W₁ =-121*0.01 + 62*0.09 + 245*0.2 + 245*0.3 + 245*0.3 + 245*0.1 = 224.87,

W₂ = 305.22, W₃ = 330.675, W₄ = 301.12

и выбор максимального значения обнаруживает оптимальность варианта 40 станков с ожидаемой прибылью 330.675 тыс.руб.

Критерий Лапласа

Если нет достаточных оснований считать, что вероятности того или иного спроса имеют неравномерное распределение, то они принимаются одинаковыми и задача сводится к поиску варианта, дающего

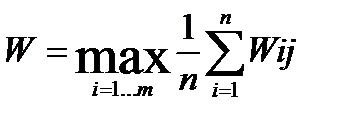
Для нашего примера

W₁ = (-121 + 62 + 245 + 245 + 245 + 245)/6 = 153.5,
W₂ = 197.25, W₃ =210.5, W₄ = 193.5

и выбор максимального значения обнаруживает оптимальность выбора варианта 40 станков с ожидаемой прибылью 210.5 тыс.руб.

Критерий Вальда

Критерий Вальда обеспечивает выбор осторожной, пессимистической стратегии. Для каждого решения X_i выбирается самая худшая ситуация (наименьшее из W_ij) и среди них отыскивается гарантированный максимальный эффект.

В нашем примере W = max(-121, -168.75, -216.5, -264.25) = -121, т.е. по этому критерию следует закупить 20 станков и максимальный возможный убыток не превысит 121 тыс.руб.

Критерий Гурвица

Критерий Гурвица предлагает некоторый компромисс:      

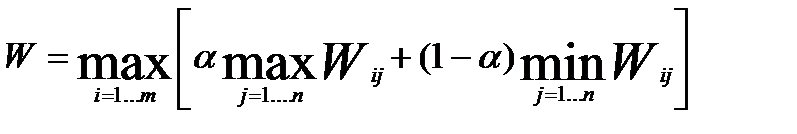, где параметр α принимает значение от 0 до 1 и выступает как коэффициент оптимизма. Так в нашем примере значения W рассчитаны для различных α:

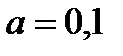
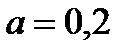
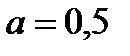
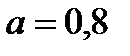
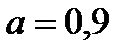
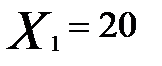
	-84,4	-47,0	62	171	206,4
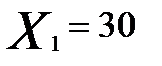
	-113,85	-58,95	105,75	270,45	325,35
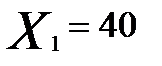
	-140,4	-70,1	149,5	369,1	442,3
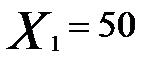
	-172,75	-81,25	193,25	467,75	559,25

При α=0.5 (равновероятных шансах на успех и неудачу) следует закупить 50 станков и ожидать прибыль порядка 193.25 тыс. руб.

При вероятности успеха 0.2 не следует закупать более 20 станков с надеждой, что убытки не превысят 47 тыс.руб.

Критерий Сэвиджа

Суть этого критерия заключается в нахождении минимального риска. При выборе решения по этому критерию сначала матрице функции полезности (эффективности) сопоставляется матрица сожалений:

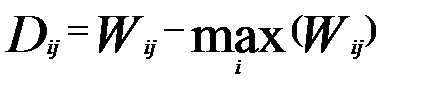
элементы которой отражают выгоду, упущенную в результате принятия i-го решения в j-м состоянии. Затем по матрице D выбирается решение по пессимистическому критерию Вальда, дающее наименьшее значение максимального сожаления.

Для нашего примера отыскиваем матрицу D, вычитая (-121) из первого столбца матрицы полезности, 62 из второго и т.д.

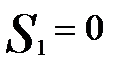
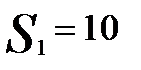
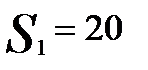
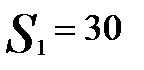
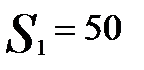
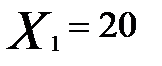
	0	0	0	-135,25	-270,5	-405,75
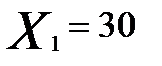
	-47,75	-47,75	-47,75	0	-135,25	-270,5
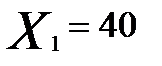
	-95,5	-95,5	-95,5	-47,75	0	-135,25
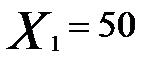
	-143,25	-143,25	-143,25	-95,5	-47,75	0

Наибольшее значение среди минимальных элементов строк здесь равно max[-405.75, -270.5, -135.25, -143.25]=-135.25 и, покупая 40 станков, мы уверены, что в худшем случае убытки не превысят 135.25 тыс.руб.

Выбор критерия нахождения оптимального решения осуществляется с учетом имеющейся информации о втором игроке и реальной ситуации.

Различные критерии приводят к различным выводам:

Возможность выбора критерия дает свободу лицам, принимающим экономические решения, при условии, что они располагают достаточными средствами для постановки подобной задачи.