Примеры задач статистики. Основные понятия и категории статистики. Предмет статистики, его особенности. Примеры на различные формы, виды и способы статистического наблюдения. Расчет ошибки наблюдения. Виды наблюдений в статистике. План статистического наблюдения, его назначение и содержание. Ряды распределения. Построение ряда распределения.
Основные понятия, на которые следует обратить внимание при изучении темы: понятия и категории статистики, статистическое наблюдение, ряды распределения.
Практическое задание №1 « Определение средних и предельных ошибок при различных видах выборочных наблюдений»
Задача 1. В механическом цехе завода в десяти бригадах работает 100 рабочих. В целях изучения квалификации рабочих была произведена 20%-ная серийная бесповторная выборка, в которую вошли 2 бригады. Получено следующее распределение обследованных рабочих по разрядам:
| Рабочие | Разряды рабочих в бригаде 1 | Разряды рабочих в бригаде 2 | Рабочие | Разряды рабочих в бригаде 1 | Разряды рабочих в бригаде 2 |
| 1 | 2 | 3 | 6 | 6 | 4 |
| 2 | 4 | 6 | 7 | 5 | 2 |
| 3 | 5 | 1 | 8 | 8 | 1 |
| 4 | 2 | 5 | 9 | 4 | 3 |
| 5 | 5 | 3 | 10 | 5 | 2 |
Необходимо определить с вероятностью 0,997 пределы, в которых находится средний разряд рабочих механического цеха.
Задача 2. 200 ящиков деталей упакованы по 40 шт. в каждом. Для проверки качества деталей был проведен сплошной контроль деталей в 20 ящиках (выборка бесповторная). В результате контроля установлено, что доля бракованных деталей составляет 15%. Межсерийная дисперсия равна 49. С вероятностью 0,997 определить пределы, в которых находится доля бракованной продукции в партии ящиков.
Задача 3. Для определения среднего процента выполнения норм выработки проведена 5%-ная типическая выборка из трех групп рабочих с разным стажем. Результаты следующие:
| Группа рабочих со стажем, лет | Объем выборки, чел., ni | Средний процент выполнения норм
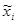
| Среднее квадратическое отклонение, %, si |
| 1-2 | 15 | 98 | 3 |
| 3-5 | 20 | 102 | 2 |
| Более 5 | 65 | 104 | 4 |
Определить: 1)средний процент выполнения норм для всех рабочих в выборочной совокупности; 2) вероятность того, что выборочная средняя (процент выполнения норм) отличается от генеральной не более чем на 1%.
Задача 4. Из партии готовой продукции в порядке механической выборки проверено 50 лампочек на продолжительность горения. Последняя оказалась равна 840 ч при среднем квадратическом отклонении 60 ч. Определить: 1) среднюю ошибку (m) выборочной средней продолжительности горения лампочки; 2) с вероятностью 0,95 доверительные пределы продолжительности горения лампочки в генеральной совокупности.
Задача 5. На городской телефонной станции в порядке собственно случайной выборки проведено 100 наблюдений и установлено, что средняя продолжительность одного телефонного разговора составляет 10 мин при среднем квадратическом отклонении 5 мин.
Определить: 1) с вероятностью 0,997 доверительные пределы для генеральной средней; 2) можно ли считать данную выборку репрезентативной?
Задача 6. На машиностроительном заводе с числом рабочих 5000 человек было проведено 4 %-ное выборочное обследование квалификации рабочих методом случайного бесповторного отбора. В результате обследования получены следующие данные:
| квалификация рабочих (тарифный разряд) | 1 | 2 | 3 | 4 | 5 | 6 |
| число рабочих | 10 | 30 | 40 | 70 | 30 | 20 |
С вероятностью 0,997 определите пределы, в которых находится средний тарифный разряд рабочих завода.
Задача 7. При обследовании 500 образцов изделий, отобранных из партии готовой продукции предприятия в случайном порядке, 40 оказались нестандартными. С вероятностью 0,954 определите пределы, в которых находится доля нестандартной продукции, выпускаемой заводом.
Задача 8. Для выявления затрат времени на обработку деталей рабочими разных квалификаций на заводе была произведена 10 %-ная типическая выборка пропорционально численности выделенных групп (внутри типичных по специальности групп произведен механический отбор). Результаты обследования представлены в таблице.
| Группы рабочих по квалификации | Число рабочих в выборке | Средние затраты времени на обработку одной детали, мин. | Среднее квадратическое отклонение |
| 1 | 60 | 10 | 1 |
| 2 | 120 | 14 | 4 |
| 3 | 80 | 20 | 2 |
| 4 | 40 | 25 | 6 |
С вероятностью 0,954 определите пределы, в которых находятся средние затраты времени на обработку деталей рабочими завода.
Задача 9. С целью определения доли брака по всей партии изготовленных деталей была произведена типическая выборка с отбором единиц пропорционально численности единиц типических групп. Внутри типических групп применялся метод механического отбора. Результаты выборки представлены в таблице:
| Тип станка | Выработка одного станка, шт. | Процент брака по данным выборки |
| 1 | 1500 | 2,0 |
| 2 | 2000 | 3,0 |
| 3 | 4000 | 1,5 |
| 4 | 5000 | 1,0 |
| 5 | 2500 | 1,8 |
С вероятностью 0,997 определите пределы, в которых находятся доля брака во всей партии деталей, изготовленных на всех станках.
Задача 10. Из совокупности, разбитой на 100 равных по величине серий, методом механического отбора отобрано 10 серий. Межсерийная дисперсия равна 20, а средняя величина признака в выборке – 140. С вероятностью 0,997 определите пределы, в которых находится генеральная средняя.
Задача 11. При изучении естественной убыли произведено 5%-ное выборочное обследование партии хранящихся на складе товаров с помощью механического отбора. В результате анализа установлено следующее распределение образцов.
| Процент естественной убыли, % | Количество образцов, шт. |
| до 4 | 5 |
| 4-6 | 10 |
| 6-8 | 20 |
| 8-10 | 50 |
| свыше10 | 15 |
| Итого | 100 |
Определите: А) среднюю ошибку выборочной доли продукции с естественной убылью от 10% и выше (размер нестандартной продукции); Б) средняя ошибка выборочного среднего процента естественной убыли.
Задача 12. При проведении выборки объемом 100 шт. методом случайного повторного отбора средняя длина детали 10 мм и дисперсия 4 мм. Определите с вероятностью 0,683 предельную ошибку выборки.
Задача 13. На основании результатов выборочного обследования рабочих предприятия с помощью 10% бесповторного типического отбора
| Цех | Всего рабочих, чел. | Обследовано, чел. | Число дней временной нетрудоспособности за год | |
| среднее значение | дисперсия | |||
| 1 | 200 | 20 | 20 | 49 |
| 2 | 500 | 50 | 11 | 25 |
| 3 | 300 | 30 | 15 | 16 |
| Итого | 1000 | 100 | ||
Определите среднюю ошибку типического бесповторного отбора.
Задача 14. Выборочное обследование 5 рабочих малого предприятия показало, что на выполнение одной из производственных операций рабочие затрачивали времени (мин.):
3, 2, 3, 5, 2.
Определите среднюю ошибку малой выборки.
Таблица 1
Индивидуальные варианты заданий
| Порядковый номер студента в группе | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Номер задачи | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Номер задачи | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Порядковый номер студента в группе | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Номер задачи | 11 | 12 | 13 | 14 | 1 | 2 | 3 | 4 | 5 | 6 |
| Номер задачи | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Порядковый номер студента в группе | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Номер задачи | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 1 | 2 |
| Номер задачи | 11 | 12 | 13 | 14 | 1 | 2 | 3 | 4 | 5 | 6 |
Практическое задание №2 «Определение численности выборки при различных способах ее проведения»
Задача 1. На заводе, имеющем 200 бригад, проектируется серийная выборка для установления доли рабочих завода, выполняющих норму выработки. Требуется определить необходимую численность выборки, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 5%. если межсерийная дисперсия доли равна 225.
Задача 2. В городе 12 тыс. жителей. Из них 7 тыс. женщин и 5 тыс. мужчин. С целью определения доли жителей в возрасте старше 60 лет предполагается провести типическую выборку жителей с пропорциональным отбором. Отбор внутри типов механический. Какое количество жителей необходимо отобрать, чтобы с вероятностью 0,997 ошибка выборки не превышала 5%? На основе предыдущих обследований известно, что дисперсия типической выборки 1600.
Задача 3. Намечается провести выборочное обследование покупателей в одном из крупных универмагов города в целях определения доли покупателей из других городов. Каким должен быть объем выборки, чтобы с вероятностью 0,954 можно было гарантировать точность результатов до 5%?
Задача 4. Какой должна быть необходимая численность выборки (при механическом отборе), проводимой в целях определения доли единиц в генеральной совокупности, обладающих тем или иным признаком, чтобы с вероятностью 0,954 можно было гарантировать ошибку доли не более 3%. Дисперсия доли неизвестна.
Ответ дать в предположении, что генеральная совокупность содержит: а) 1000 единиц; б) 10 000 единиц — либо численность ее неизвестна.
Задача 5. Определить, какое количество продукции (изделий) следует подвергнуть выборочному обследованию для определения среднего срока службы, чтобы с вероятностью 0,9545 относительная предельная ошибка выборки не превысила 5%. Коэффициент вариации среднего срока службы изделий по пробной выборке составил 30%, а вся партия обследуемой продукции состоит из 2000 единиц.
Задача 6. На склад поступило 100 ящиков готовых изделий по 80 шт. в каждом. На основе предыдущих обследований известно, что дисперсия серийной выборки равна 5. Для установления среднего веса деталей следует провести серийную выборку деталей методом механического отбора так, чтобы с вероятностью 0,954 ошибка выборки не превышала 2 г. Определите объем выборки.
Задача 7. На заводе 2000 рабочих. Из них 1500 мужчин и 500 женщин. С целью определения доли рабочих, которые проработали на заводе более 5 лет, предполагается провести типическую выборку рабочих с пропорциональным отбором. Отбор внутри групп механический. Какое число рабочих необходимо отобрать, чтобы с вероятностью 0,683 ошибка выборки не превышала 3%, если на основе обследований известно, что дисперсия типической выборки равна 2100?
Задача 8. На заводе предполагается провести выборочное обследование средней часовой выработки рабочих методом случайного повторного отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала 5 шт., если на основе предыдущих обследований известно, что дисперсия равна 225.
Задача 9. На заводе с числом рабочих 15 тыс. человек в порядке механической выборки предполагается определить долю рабочих со стажем работы 20 лет и более. Какова должна быть численность выборки, чтобы с вероятностью 0, 954 ошибка выборки не превышала 0,03, если на основе предыдущих обследований известно, что дисперсия равна 0,2?
Задача 10. Совокупность разбита на 100 серий. Межсерийная дисперсия равна 20. Сколько серий надо отобрать бесповторным методом, чтобы с вероятностью 0,997 ошибка выборочной средней не превысила 4?
Таблица 2
Индивидуальные варианты заданий
| Порядковый номер студента в группе | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Номер задачи | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Номер задачи | 5 | 6 | 7 | 8 | 9 | 10 | 1 | 2 | 3 | 4 |
| Порядковый номер студента в группе | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Номер задачи | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Номер задачи | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 1 | 2 | 3 |
| Порядковый номер студента в группе | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Номер задачи | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Номер задачи | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 1 | 2 |
Контрольные вопросы
1. Какие Вы знаете виды выборок?
2. От каких факторов зависит средняя ошибка выборки?
3. Как определяется предельная ошибка выборки?
4. Определение средней ошибки собственно-случайной выборки при повторном и бесповторном отборе.
5. Как определяется средняя ошибка механической выборки?
6. Особенности определения средней и предельной ошибки серийной выборки.
7. Как определяется средняя ошибка типического отбора?
8. От каких факторов зависит численность выборки?
9. Проблемы определения численности выборки.
10. Подходы к определению численности выборки.
11. Как определяется численность собственно-случайной выборки при повторном и бесповторном отборе?
12. Как определяется численность механической выборки?
13. Как определяется численность типической выборки при повторном и бесповторном отборе?
14. Как определяется численность серийной выборки при повторном и бесповторном отборе?
Практическое задание № 3. Построение графиков интервальных рядов.
На сайте Росстата возьмите данные о среднемесячной номинальной начисленной заработной плате работников в соответствующем варианту федеральном округе за прошедший год.
Таблица 1
Например: Среднемесячная номинальная начисленная заработная плата работников
в целом по экономике по ПФО в 2013 году
| Регион | ЗП, руб. |
| Республика Башкортостан | 22440,2 |
| Республика Марий Эл | 18558,3 |
| Республика Мордовия | 17885,3 |
| Республика Татарстан | 26012,0 |
| Удмуртская Республика | 21415,1 |
| Чувашская Республика | 19423,8 |
| Пермский край | 24790,7 |
| Кировская область | 19332,7 |
| Нижегородская область | 23802,0 |
| Оренбургская область | 21543,2 |
| Пензенская область | 20649,3 |
| Самарская область | 23432,5 |
| Саратовская область | 20474,8 |
| Ульяновская область | 19217,8 |
Сформировать интервальный ряд распределения. Построить графики полигона распределения, гистограмму, кумуляту, огиву.
Контрольные вопросы
- Что такое полигон распределения?
- Что такое кумулята?
- Что такое огива?
- Как построить соответствующие графики?
Дата: 2019-02-02, просмотров: 475.