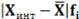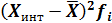Основные понятия, на которые следует обратить внимание при изучении темы: понятия и категории статистики, статистическое наблюдение, ряды распределения.
Пример решения практических задач.
В табл. 1 приведены данные о среднемесячной номинальной начисленной заработной плате работников в Приволжском федеральном округе за 2013 год.
Таблица 1
Среднемесячная номинальная начисленная заработная плата работников
в целом по экономике по ПФО в 2013 году
| Регион | ЗП, руб. |
| Республика Башкортостан | 22440,2 |
| Республика Марий Эл | 18558,3 |
| Республика Мордовия | 17885,3 |
| Республика Татарстан | 26012,0 |
| Удмуртская Республика | 21415,1 |
| Чувашская Республика | 19423,8 |
| Пермский край | 24790,7 |
| Кировская область | 19332,7 |
| Нижегородская область | 23802,0 |
| Оренбургская область | 21543,2 |
| Пензенская область | 20649,3 |
| Самарская область | 23432,5 |
| Саратовская область | 20474,8 |
| Ульяновская область | 19217,8 |
Сформировать интервальный ряд распределения. Построить графики полигона распределения, гистограмму, кумуляту, огиву.
Решение:
Оптимальное число интервалов для заданного числа наблюдений (N=14) рассчитаем по формуле Стерджесса:
n=1+3,322log(N)=4,8
Итак, сформируем интервальную группировку с числом интервалов n=4.
Определим размах вариации:
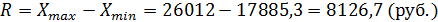
Определим размах интервала:
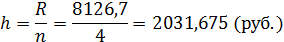
Сформируем интервальный ряд распределения (табл. 2), где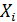 
– значение признака, 
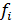– частота, 
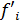– накопленная частота.
Таблица 2
Интервальный ряд распределения
| Xi | fi | f ’ i |
| 17885,3 – 19916,975 | 5 | 5 |
| 19916,975 – 21948,65 | 4 | 9 |
| 21948,65 – 23980,325 | 2 | 11 |
| 23980,325 – 26012 | 3 | 14 |
Сумма
14
Для построения графиков используем программу MS Excel.
Для построения полигона на оси абсцисс откладывают значения варьирующего признака, а на оси ординат – частоты. Тип графического представления в Excel следует выбирать «График». Аналогично строится гистограмма, но с выбором типа графика «Гистограмма». Для построения кумуляты значения варьирующего признака откладываются по оси абсцисс, а на оси ординат помещаются накопленные итоги частот. Для построения огивы на оси ординат помещаются накопленные итоги частот в обратном порядке. В обоих случаях в программе Excel следует выбирать тип «График».
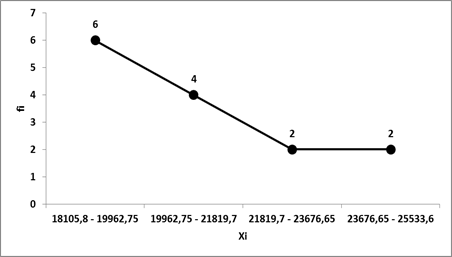
Рис. 1 Полигон распределения
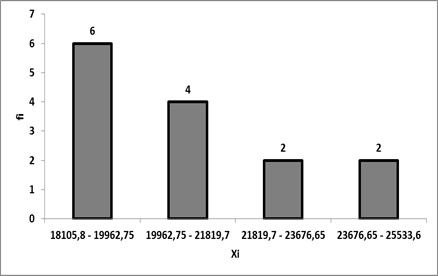
Рис. 2 Гистограмма
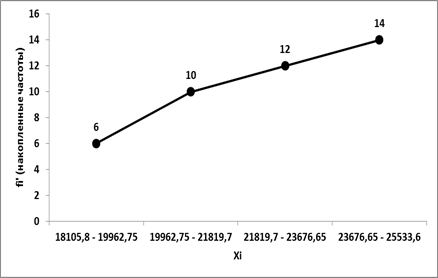
Рис. 3 Кумулята
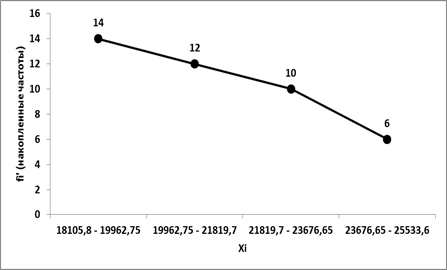
Рис. 4 Огива
Тема 2. Абсолютные и относительные величины
Основные понятия, на которые следует обратить внимание при изучении темы: абсолютные и относительные статистические показатели, средние величины и их показатели, стандартное отклонение, дисперсия, коэффициент вариации.
Пример решения практических задач.
Задача. По данным о распределении субъектов Приволжского федерального округа по величине номинальной начисленной заработной платы работников в 2013 году (табл. 2) необходимо:
а) рассчитать среднюю величину;
б) определить типичность средней величины с помощью линейного и квадратического коэффициентов вариации.
в) рассчитать моду.
г) рассчитать медиану.
Решение:
а) средняя величина:
Для расчетов используем формулу средней арифметической взвешенной:
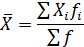
Т.к. расчет ведется по интервальной группировке, в формуле используем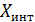 
– середину интервала.
Построим вспомогательную расчетную таблицу (все промежуточные расчеты целесообразно осуществлять в программе MS Excel):
Таблица 5
| Xi | fi | Xинт | Xинтfi |
| 17885,3 – 19916,975 | 5 | 18901,14 | 94505,6875 |
| 19916,975 – 21948,65 | 4 | 20932,81 | 83731,25 |
| 21948,65 – 23980,325 | 2 | 22964,49 | 45928,975 |
| 23980,325 – 26012 | 3 | 24996,16 | 74988,4875 |
Сумма
14
299154,4
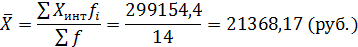
Т.е. средняя номинальная начисленная заработная плата работников в субъектах ПФО в 2013 г. составляла 21368,17 рублей.
б) определение типичности средней величины с помощью коэффициентов вариации:
– линейный коэффициент вариации (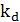 
):
Построим вспомогательную расчетную таблицу (все промежуточные расчеты целесообразно осуществлять в программе MS Excel):
Таблица 6
| Xi | fi | Xинт |
|
| 17885,3 – 19916,975 | 5 | 18901,14 | 12335,16964 |
| 19916,975 – 21948,65 | 4 | 20932,81 | 1741,44 |
| 21948,65 – 23980,325 | 2 | 22964,49 | 3192,632143 |
| 23980,325 – 26012 | 3 | 24996,16 | 10883,97321 |
Сумма
14
28153,21
Среднее линейное отклонение (d) рассчитаем по формуле:
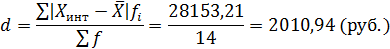
Линейный коэффициент вариации:
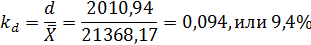
Т.к.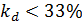 
,следовательно, найденная средняя величина типична для рассматриваемой совокупности.
– квадратический коэффициент вариации:
Построим вспомогательную расчетную таблицу (все промежуточные расчеты целесообразно осуществлять в программе MS Excel):
Таблица 7
| Xi | fi | Xинт |
|
| 17885,3 – 19916,975 | 5 | 18901,14 | 30431282,02 |
| 19916,975 – 21948,65 | 4 | 20932,81 | 758149,59 |
| 21948,65 – 23980,325 | 2 | 22964,49 | 5096450 |
| 23980,325 – 26012 | 3 | 24996,16 | 39486957,64 |
Сумма
14
75772839,25
Среднее квадратическое отклонение (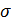 
) рассчитаем по формуле:
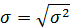
где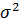 
– дисперсия.
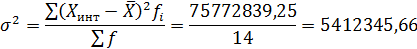
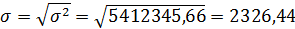
Квадратический коэффициент вариации (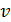 
):
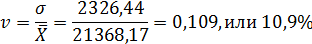
Т.к.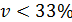 
,следовательно, найденная средняя величина типична для рассматриваемой совокупности.
в) расчет моды:
Модальный интервал – это интервал с наибольшей частотой fi, т.е. интервал 17885,3 – 19916,975):
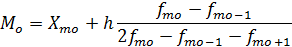
где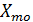 
– нижняя граница модального интервала;
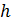– размах интервала;
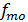– частота признака в модальном интервале;
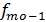– частота признака в интервале, предшествующем модальному;
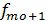– частота признака в интервале, следующем за модальным.
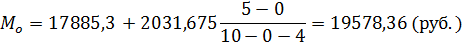
Т.е. наиболее часто встречаемая номинальная начисленная заработная плата в субъектах ПФО в 2013 г. составляла 19578,36 рублей.
г) расчет медианы:
Медианный интервал – это интервал, приходящийся на середину ряда распределения, т.е. интервал 19916,975 – 21948,65.
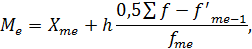
где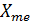 
– нижняя граница медианного интервала;
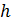– размах интервала;
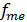– частота признака в медианном интервале;
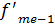– частота признака, накопленная до начала медианного интервала.
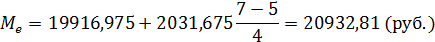
Т.е. половина субъектов ПФО в 2013 г. имела номинальную начисленную заработную плату меньше 20932,81 рублей, а половина – больше этого значения.
Тема 3. Индексы.
Основные понятия, на которые следует обратить внимание при изучении темы: индивидуальные и общие индексы, базисные, цепные и средние показатели.
Пример решения практических задач.
В табл. 16 приведены данные о продажах двух видов товара:
Таблица 16
Товар
Цена за шт., тыс. руб.
Объем продаж, шт.
Определить: 1) индивидуальные индексы цен, физического объема и выручки; 2) общие индексы цен, физического объема и выручки; 3) выполнить факторный анализ выручки, определить абсолютное изменение выручки за счет изменений цен, структурного сдвига и объемов продаж.
Решение:
Начнем решение задачи с определения выручки и ее абсолютного и относительного изменения.
Выручка определяется по формуле:
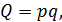
где p – цена товара;
q – физический объем (количество);
Q – выручка (товарооборот).
Рассчитаем выручку по каждому товару в 1 кв. 2014 г. (Q 0 j) и во 2 кв. 2014 г. (Q 1 j) в табл. 17.
Таблица 17
| Товар j | 1 кв. 2014 г. Q 0 j | 2 кв. 2014 г. Q 1 j | Изменение выручки ∆ Qj = Q 1 j – Q 0 j |
| Смартфоны | 20*100 = 2000 | 18*160 = 2880 | 880 |
| Планшеты | 22*150 = 3300 | 25*120 = 3000 | -300 |
| Итого | 5300 | 5880 | 580 |
Из таблицы видно, что абсолютное изменение общей выручки составило: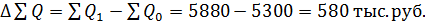 
, то есть она выросла на 580 тыс. руб.
Общий индекс изменения выручки равняется:
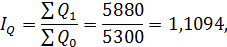
то есть выручка от продажи товаров увеличилась в 1,1094 раза или на 10,94% во 2 кв. 2014 г. по сравнению с 1 кв. 2014 г.
1. Индивидуальные индексы.
Индивидуальный индекс цен (ip):
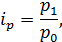
где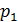 
– значение цены в отчетном периоде;
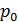– значение цены в базисном периоде.
Индивидуальный индекс физического объема (iq):
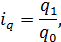
где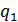 
– значение количества проданного товара в отчетном периоде;
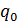– значение количества проданного товара в базисном периоде.
Индивидуальный индекс выручки (iQ):
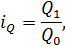
где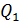 
– значение выручки в отчетном периоде;
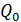– значение выручки в базисном периоде.
Индивидуальный индекс доли товара (id):
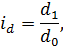
где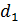 
– значение доли товара в отчетном периоде;
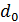– значение доли товара в базисном периоде.
Результаты расчетов представим в табл. 18.
Таблица 18
| Индивидуальный индекс | Смартфоны | Планшеты |
| количества iq | 160/100 = 1,6 | 120/150 = 0,8 |
| отпускных цен ip | 18/20 = 0,9 | 25/22 = 1,136 |
| выручки iQ | 2880/2000=1,44 | 3000/3300=0,909 |
| доли товара id | (160/280)/(100/250) = 1,429 | (120/280)/(150/250) = 0,714 |
Из таблицы видно, что в 1 кв. 2014 г. по сравнению со 2 кв. 2014 г.:
– количество проданных смартфонов увеличилось в 1,6 раза или на 60%, а планшетов – уменьшилось в 0,8 раза или на 20%;
– цена смартфонов понизилась в 0,9 раза или на 10%, а планшетов – повысилась в 1,136 раза или на 13,6%;
– выручка по смартфонам выросла в 1,44 раза или на 44%, а по планшетам – снизилась в 0,909 раза или на 9,1%;
– доля проданных смартфонов увеличилась в 1,429 раза или на 42,9%, а планшетов – уменьшилась в 0,714 раза или на 28,6%.
2. Общие индексы.
Агрегатный общий индекс физического объема Ласпейреса определяется по формуле:
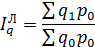
В нашей задаче:
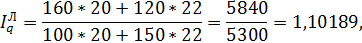
то есть количество проданных товаров в базисных ценах выросло в 1,10189 раза или на 10,189% во 2 кв. 2014 г. по сравнению с 1 кв. 2014г.
Агрегатный общий индекс цен Пааше рассчитывается по формуле:
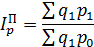
В нашей задаче:
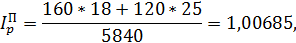
то есть цена проданных товаров при объемах продаж отчетного периода выросла в 1,00685 раза или на 0,685% во 2 кв. 2014 г. по сравнению с 1 кв. 2014г.
Контроль осуществляется по формуле: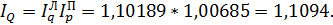 
Агрегатный общий индекс цен Ласпейреса вычисляется по формуле:
= 
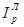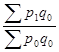
В нашей задаче =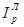 
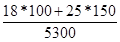= 5550/5300 = 1,04717, то есть цена проданных товаров при объемах продаж базисного периода выросла в 1,04717 раза или на 4,717% во 2 кв. 2014 г. по сравнению с 1 кв. 2014г.
Агрегатный общий количественный индекс Пааше рассчитывается по формуле:
= 
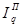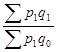
В нашей задаче 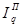= 5880/5550 =1,05946, то есть количество проданных товаров в отчетных ценах выросло в 1,05946 раза или на 5,946% во 2 кв. 2014 г. по сравнению с 1 кв. 2014г.
Контроль осуществляется по формуле: IQ = 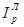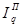= 1,04717*1,05946 =1,1094.
Средняя геометрическая величина определяется из индексов Ласпейреса и Пааше (по методике Фишера) для количества товаров по формуле:
= 
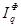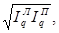
а для цен по формуле:
= 
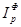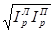
В нашей задаче =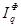 
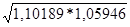=1,0805, то есть в среднем количество проданных товаров выросло в 1,0805 раза или на 8,05%; = 
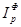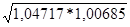=1,0268, то есть в среднем цена проданных товаров выросла в 1,0268 раза или на 2,68%.
Далее выполняется факторный анализ общей выручки. В его основе лежит следующая трехфакторная мультипликативная модель выручки:
IQ =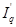 
,
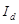
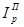где =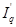 
,
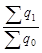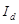– индекс структурных сдвигов, показывающий как изменилась выручка под влиянием фактора изменения долей проданных фруктов в отчетном периоде по сравнению с базисным периодом. Он определяется по формуле:
= 
= 
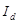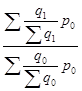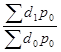
В нашей задаче =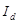 
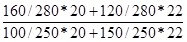= 0,9838, то есть структурный сдвиг должен был уменьшить отчетную выручку в базисных ценах в 0,9838 раза или на 1,62%.
Тогда изменение выручки за счет изменения общего количества товаров определяется по формуле (74):
= 
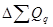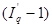
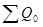
В нашей задаче 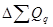= (1,12-1)*5300 = 636 (тыс. руб.), то есть изменение количества проданных товаров увеличило выручку на 636 тыс. руб.
Изменение общей выручки за счет структурных сдвигов находится по формуле:
= 
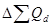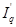
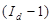
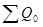
В нашей задаче 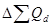= 1,12*(0,9838-1)*5300 = –96 (тыс. руб.), то есть структурный сдвиг в количестве проданных товаров уменьшил выручку на 96 тыс. руб.
Изменение общей выручки за счет изменения отпускных цен рассчитывается по формуле:
= 
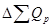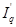
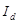
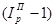
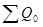
В нашей задаче 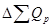=1,12*0,9838*(1,00685-1)*5300 = 40 (тыс. руб.), то есть изменение цен на товары увеличило выручку на 40 тыс. руб.
Контроль правильности расчетов производится по формуле, согласно которой общее изменение выручки равно сумме ее изменений за счет каждого фактора в отдельности:
= 
- = + +
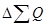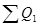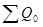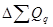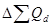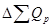
В нашей задаче 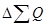= 636 + (–96) + 40 = 580 тыс. руб.
Результаты факторного анализа общей выручки занесем в табл. 19.
Таблица 19
Товар
j
Изменение выручки,
Тыс. руб.
В том числе за счет
Дата: 2019-02-02, просмотров: 205.
