Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Нерекурсивный алгоритм сложнее рекурсивного.

1. Находится место вставки и вершина, высота которой не изменится при вставке (это вершина, у которой высота левого поддерева не равна высоте правого; будем называть её PrimeNode)
2. Выполняется спуск от PrimeNode до места вставки с изменением балансов
3. Выполняется ребалансировка PrimeNode при наличии переполнения

Нерекурсивное удаление из АВЛ-дерева сверху вниз

Для реализации удаления будем исходить из того же принципа, что и при вставке: найдём вершину, удаление из которой не приведёт к изменению её высоты. Существует два случая:

1. высота левого поддерева равна высоте правого поддерева (исключая случай, когда у листа нет поддеревьев)
2. высота дерева по направлению движения меньше противоположной(«брат» направления) и баланс «брата» равен 0 (разбор этого варианта довольно сложен, так что пока без доказательства)

Для облегчения понимания приведённый алгоритм не содержит каких-либо оптимизаций. В отличие от рекурсивного алгоритма, найденная удаляемая вершина заменяется значением из левой подветви. Этот алгоритм можно оптимизировать так же, как и рекурсивный (за счёт того, что после нахождения удаляемой вершины известно направление движения):

1. ищем удаляемый элемент и попутно находим нашу замечательную вершину
2. производим изменение балансов, в случае необходимости делаем ребалансировку
3. удаляем наш элемент (в действительности не удаляем, а заменяем его ключ и значение, учёт перестановок вершин будет немного сложнее)

Расстановка балансов при удалении

Как уже говорилось, если удаляемая вершина — лист, то она удаляется, и обратный обход дерева происходит от родителя удалённого листа. Если не лист — ей находится «замена», и обратный обход дерева происходит от родителя «замены». Непосредственно после удаления элемента — «замена» получает баланс удаляемого узла.

При обратном обходе: если при переходе к родителю пришли слева — баланс увеличивается на 1, если же пришли справа — уменьшается на 1.

Это делается до тех пор, пока при изменении баланса он не станет равным −1 или 1 (обратите внимание на различие с вставкой элемента!): в данном случае такое изменение баланса будет гласить о неизменной дельта-высоте поддеревьев. Повороты происходят по тем же правилам, что и при вставке.

Расстановка балансов при одинарном повороте

Обозначим:

• «Current» — узел, баланс которого равен −2 или 2: то есть тот, который нужно повернуть (на схеме — элемент a)
• «Pivot» — ось вращения. +2: левый сын Current’а, −2: правый сын Current’а (на схеме — элемент b)

Если поворот осуществляется при вставке элемента, то баланс Pivot’а равен либо 1, либо −1. В таком случае после поворота балансы обоих устанавливаются равными 0. При удалении всё иначе: баланс Pivot’а может стать равным 0 (в этом легко убедиться).

Приведём сводную таблицу зависимости финальных балансов от направления поворота и исходного баланса узла Pivot:

Направление поворота	Old Pivot.Balance	New Current.Balance	New Pivot.Balance
Левый или Правый	-1 или +1	0	0
Правый	0	-1	+1
Левый	0	+1	-1

Расстановка балансов при двойном повороте

Pivot и Current — те же самые, но добавляется третий участник поворота. Обозначим его за «Bottom»: это (при двойном правом повороте) левый сын Pivot’а, а при двойном левом — правый сын Pivot’а.

При данном повороте — Bottom в результате всегда приобретает баланс 0, но от его исходного баланса зависит расстановка балансов для Pivot и Current.

Приведём сводную таблицу зависимости финальных балансов от направления поворота и исходного баланса узла Bottom:

Направление	Old Bottom.Balance	New Current.Balance	New Pivot.Balance
Левый или Правый	0	0	0
Правый	+1	0	-1
Правый	-1	+1	0
Левый	+1	-1	0
Левый	-1	0	+1

Оценка эффективности

Из формулы, приведённой выше, высота АВЛ-дерева никогда не превысит высоту идеально сбалансированного дерева более, чем на 45%. Для больших n {\displaystyle n} имеет место оценка 1.04 log 2 ⁡ n {\displaystyle 1.04\log _{2}{n}} . Таким образом, выполнение основных операций требует порядка log 2 ⁡ n {\displaystyle \log _{2}{n}} сравнений. Экспериментально выяснено, что одна балансировка приходится на каждые 2 включения и на каждые 5 исключений.

См. также

Сбалансированные (самобалансирующиеся) деревья:

• Красно-чёрное дерево
• Матричное дерево
• Идеально сбалансированное дерево
• Расширяющееся дерево
• Список структур данных (деревья)

 

 

Расширяющееся дерево

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 сентября 2016; проверки требуют 2 правки.

Расширяющееся дерево

Тип

Дерево

Изобретено в

1985 году

Изобретено

Дэниел Слитор и Роберт Андре Тарьян

Временная сложность
в О-символике

  В среднем В худшем случае Расход памяти O(n) O(n) Поиск O(log n) O(log n) Вставка O(log n) O(log n) Удаление O(log n) O(log n)

Расширяющееся (англ. splay tree) или косое дерево является двоичным деревом поиска, в котором поддерживается свойство сбалансированности. Это дерево принадлежит классу «саморегулирующихся деревьев», которые поддерживают необходимый баланс ветвления дерева, чтобы обеспечить выполнение операций поиска, добавления и удаления за логарифмическое время от числа хранимых элементов. Это реализуется без использования каких-либо дополнительных полей в узлах дерева (как, например, в Красно-чёрных деревьях или АВЛ-деревьях, где в вершинах хранится, соответственно, цвет вершины и глубина поддерева). Вместо этого «расширяющие операции» (splay operation), частью которых являются вращения, выполняются при каждом обращении к дереву.

Учётная стоимость (англ.) в расчёте на одну операцию с деревом составляет O ( log ⁡ n ) {\displaystyle O(\log n)} .

Расширяющееся дерево придумали Роберт Тарьян и Даниель Слейтор в 1983 году.

Содержание

• 1 Операции
• 1.1 Splay (расширение)
• 1.2 Search (поиск элемента)
• 1.3 Insert (добавление элемента)
• 1.4 Delete (удаление элемента)
• 1.5 Merge (объединение двух деревьев)
• 1.6 Split (разделение дерева на две части)
• 2 Реализация
• 3 Примечание
• 4 См. также
• 5 Литература

Операции

В другом языковом разделе есть более полная статья Splay tree (англ.) Вы можете помочь проекту, расширив текущую статью с помощью перевода. При этом, для соблюдения правил атрибуции, следует установить шаблон {{Переведённая статья}} на страницу обсуждения, либо указать ссылку на статью-источник в комментарии к правке.

Splay (расширение)

Основная операция дерева. Заключается в перемещении вершины в корень при помощи последовательного выполнения трёх операций: Zig, Zig-Zig и Zig-Zag. Обозначим вершину, которую хотим переместить в корень за x, её родителя — p, а родителя p (если существует) — g.

Zig: выполняется, когда p является корнем. Дерево поворачивается по ребру между x и p. Существует лишь для разбора крайнего случая и выполняется только один раз в конце, когда изначальная глубина x была нечётна.

Zig-Zig: выполняется, когда и x, и p являются левыми (или правыми) сыновьями. Дерево поворачивается по ребру между g и p, а потом — по ребру между p и x.

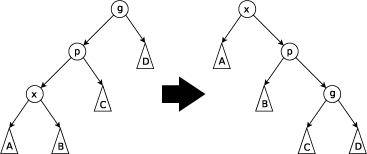
Zig-Zag: выполняется, когда x является правым сыном, а p — левым (или наоборот). Дерево поворачивается по ребру между p и x, а затем — по ребру между x и g.

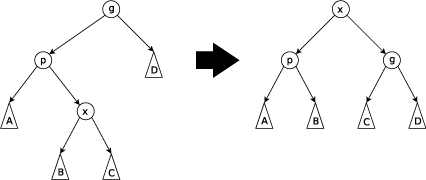
Search (поиск элемента)

Поиск выполняется как в обычном двоичном дереве поиска. При нахождении элемента запускаем Splay для него.

Insert (добавление элемента)

Вставка происходит как в обычном бинарном дереве поиска, после, запускаем Split() от добавляемого элемента и подвешиваем получившиеся деревья за него.

Delete (удаление элемента)

Находим элемент в дереве, делаем Splay для него, делаем текущим деревом Merge его детей.

Merge (объединение двух деревьев)

Для слияния деревьев T1 и T2, в которых все ключи T1 меньше ключей в T2, делаем Splay для максимального элемента T1, тогда у корня T1 не будет правого ребенка. После этого делаем T2 правым ребенком T1.