Соотношение с технологическими укладами

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Экономические циклы

Название цикла Характерный период Цикл Китчина 3—4 года Цикл Жюгляра 7—11 лет Цикл Кузнеца 15—25 лет Цикл Кондратьева 45—60 лет

ЦИКЛЫ КИТЧИНА

- короткие (продолжительностью около 4 лет) экономические циклы, связанные с движением товарно-материальных запасов. Смысл Ц. К. в следующем: увеличение размеров реальных инвестиций в основной капитал вызывает превышение товарных запасов над потребностью в них. В этом случае спрос на инвестиции падает и начинается замедление темпов роста производства. Т. о., Ц. К. связаны с восстановлением равновесия на потребительском и инвестиционном рынках. Названы именем англ. статистика Джозефа Китчина (1861-1932), который ввел их в экономическую теорию.

Циклы Жюгляра

Циклы Жюгляра — среднесрочные экономические циклы с характерным периодом в 7—11 лет. Названы по имени французского экономиста Клемана Жюгляра, одним из первых описавшего эти циклы^[1]. В отличие от циклов Китчина в рамках циклов Жюгляра мы наблюдаем колебания не просто в уровне загрузки существующих производственных мощностей (и, соответственно, в объёме товарных запасов), но и колебания в объёмах инвестиций в основной капитал. В результате, к временным запаздываниям, характерным для циклов Китчина, здесь добавляются ещё и временные задержки между принятием инвестиционных решений и возведением соответствующих производственных мощностей (а также между возведением и актуальным запуском соответствующих мощностей). Дополнительная задержка формируется и между спадом спроса и ликвидацией соответствующих производственных мощностей. Данные обстоятельства и обуславливают то, что характерный период циклов Жюгляра оказывается заметно более продолжительным, чем характерный период циклов Китчина. Циклические экономические кризисы/рецессии могут рассматриваться в качестве одной из фаз цикла Жюгляра (наряду с фазами оживления, подъёма и депрессии). Вместе с тем от фазы кондратьевской волны зависит глубина этих кризисов^[2].

В своей работе Жюгляр приводит следующие значения данных о кризисах во Франции, Британии и США^[3]:

1803—1804
1810—1810
1813—1815—1814
1818—1818—1818
1826—1826—1826
1830—1830—1830
1836—1837—1837
1839—1839—1839
1847—1847—1848
1857—1857—1857

Поскольку чёткой периодичности не наблюдается, было взято среднее значение в 7—10 лет. Обусловленное резонансом (ускорением) или диссонансом (замедлением) векторов циклов Китчина.

Фазы цикла Жюгляра

В цикле Жюгляра достаточно часто выделяют четыре фазы, в которых некоторые исследователи выделяют подфазы:

фаза оживления (подфазы старта и ускорения);
фаза подъёма, или процветания (подфазы роста и перегрева, или бума) ;
фаза рецессии (подфазы краха/острого кризиса и спада);
фаза депрессии, или застоя (подфазы стабилизации и сдвига)^[4].

Фазы подъёма (пика) и депрессии (дна) традиционно совпадают с экстремумом подфаз - циклов Китчена.

3. Ритмы Кузнеца

Материал из Википедии — свободной энциклопедии

Циклы (ритмы) Кузнеца имеют продолжительность примерно 15—25 лет. Они получили название циклов Кузнеца по имени американского экономиста, лауреата Нобелевской премии Саймона Кузнеца. Были открыты им в 1930 году^[1].

Кузнец связывал эти волны с демографическими процессами, в частности, притоком иммигрантов и строительными изменениями, поэтому он назвал их «демографическими» или «строительными» циклами.

В настоящее время рядом авторов ритмы Кузнеца рассматриваются в качестве технологических, инфраструктурных циклов^[2]. В рамках этих циклов происходит массовое обновление основных технологий. Кроме того хорошо совпадают с циклом Кузнеца большие циклы цен на недвижимость на примере Японии 1980—2000 годов и длительность большой полуволны подъёма цен в США.

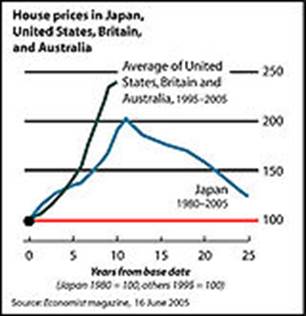
Высказывалось также и предложение рассматривать ритмы Кузнеца в качестве третьей гармоники Кондратьевской волны^[3].

В своей работе Мозес Абрамовиц приводит следующие данные касательно лет начала затяжных депрессий или стагнаций в США, соотнося их с циклами Кузнеца^[4]:

1815
1836
1853
1873
1882
1892
1907
1920
1929

Как видно из этого перечня, чёткой периодичности не наблюдается, поэтому исследователи берут среднее значение в 15—20 лет. Аналогичная ситуация и для других показателей, относящихся к труду и производству, приводимых Абрамовицом.

Циклы Кондратьева

Циклы Кондратьева (К-циклы или К-волны) — периодические циклы сменяющихся подъёмов и спадов современной мировой экономики продолжительностью 48—55 лет, описанные в 1920-е годы Николаем Кондратьевым.

Концепция активно исследуется и развивается на протяжении всего времени существования, однако широкого консенсуса в сообществе учёных-экономистов на счёт её практической применимости не достигнуто: многие исследователи (особенно в России) широко используют кондратьевские циклы в своих исследованиях, однако значительная часть экономистов их не рассматривает или прямо отвергает существование таких циклов^[1].

Содержание

1 История
2 Концепция
3 Датировки волн
4 Соотношение с технологическими укладами
5 Примечания
6 Литература
7 Ссылки

История

В 1913 году голландский экономист Якоб Ван Гельдерен (нид.)русск. в книге «Springvloed, Beschouwingenover industrielle Ontwikkeling en Prijsbewegung» разработал теорию волнообразного эволюционного развития при капитализме, в которой обосновал существование 50—60 летних циклов.

В 1922 году Кондратьев опубликовал наблюдение, согласно которому в долгосрочной динамике некоторых экономических индикаторов наблюдается определенная циклическая регулярность, в ходе которой на смену фазам роста соответствующих показателей приходят фазы их относительного спада с характерным периодом этих долгосрочных колебаний порядка 50 лет^[2] и в дальнейшем развил, охарактеризовал и обосновал обнаруженную закономерность. Исследования и выводы Кондратьева основывались на эмпирическом анализе большого числа экономических показателей различных стран на довольно длительных промежутках времени, охватывавших 100—150 лет, среди изученных показателей — индексы цен, государственные долговые бумаги, номинальная заработная плата, показатели внешнеторгового оборота, добыча угля, золота, производство свинца, чугуна^[3].

Основной оппонент Кондратьева в 1920-е — 1930-е годы Дмитрий Опарин указывал на то, что временные ряды исследованных экономических показателей, хотя и дают большие или меньшие отклонения от средней величины в ту или иную сторону в разные периоды экономической жизни, но характер этих отклонений как по отдельному показателю, так и по корреляции показателей, не позволяют выделить строгой цикличности. Прочие оппоненты указывали на отступления Кондратьева от марксизма, в частности использование им для объяснения циклов количественной теории денег, а не социальных механизмов (Лев Троцкий, например, в работе «О кривой капиталистического развития» утверждал, что периоды упадка и подъёма капиталистического хозяйства в долгосрочной перспективе обусловлены большей или меньшей напряжённостью классовой борьбы).

Основной вклад в популяризацию идей Кондратьева внёс в своих работах Йозеф Шумпетер^[4]^[5] — именно он ввёл термин «кондратьевские волны»^[6], а в 1939 году в своей книге «Деловые циклы» поддержал и развил закономерность, обнаруженную Кондратьевым, вкупе с 7—11-летними циклами производства и занятости^[7].

Интерес к исследованиям Кондратьева в среде российских экономистов возобновился после работы С. Меньшикова и Л. Клименко «Длинные волны в экономике» 1989 года. Среди учёных конца XX — начала XXI веков, применяющих кондратьевские циклы в своих исследованиях — Аскар Акаев, Лусинэ Бадалян, Сергей Глазьев, Виктор Дементьев, Виктор Криворотов, Дмитрий Львов^[8].

Концепция

Характерный период кондратьевских волн — 50 лет с возможным отклонением в 10 лет (от 40 до 60 лет), циклы состоят из чередующихся фаз относительно высоких и относительно низких темпов экономического роста. Кондратьев отметил четыре эмпирические закономерности в развитии больших циклов.

Первая — перед началом повышательной волны каждого большого цикла, а иногда в самом начале её наблюдаются значительные изменения в условиях хозяйственной жизни общества. Изменения выражаются в технических изобретениях и открытиях, в изменении условий денежного обращения, в усилении роли новых стран в мировой хозяйственной жизни. Указанные изменения в той или иной степени происходят постоянно, но, по утверждению Кондратьева, они протекают неравномерно и наиболее интенсивно выражены перед началом повышательных волн больших циклов и в их начале.

Вторая — периоды повышательных волн больших циклов, как правило, значительно богаче крупными социальными потрясениями и переворотами в жизни общества (революции, войны), чем периоды понижательных волн.

Третья — понижательные волны этих больших циклов сопровождаются длительной депрессией сельского хозяйства.

Четвёртая — большие циклы экономической конъюнктуры выявляются в том же едином процессе динамики экономического развития, в котором выявляются и средние циклы с их фазами подъёма, кризиса и депрессии^[9].

Шумпетером установлена связь между длинными циклами Кондратьева и среднесрочными циклами Жюгляра. Существует мнение, что относительная правильность чередования повышательных и понижательных фаз кондратьевских волн (каждая фаза 20—30 лет) определяется характером группы близлежащих среднесрочных циклов. Во время повышательной фазы кондратьевской волны быстрое расширение экономики неизбежно приводит общество к необходимости изменения. Но возможности изменения общества отстают от требований экономики, поэтому развитие переходит в понижательную В-фазу, в течение которой кризисно-депрессивные явления и трудности заставляют перестраивать экономические и иные отношения^[10].

Датировки волн

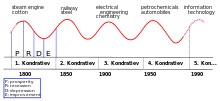
Для периода после промышленной революции обычно выделяются следующие кондратьевские волны:

1-й цикл — с 1803 до 1841—1843 годов (отмечены моменты минимумов экономических показателей мировой экономики);
2-й цикл — с 1844—1851 до 1890—1896 годов;
3-й цикл — с 1891—1896 до 1945—1947 годов;
4-й цикл — с 1945—1947 до 1981—1983 годов;
5-й цикл — с 1981—1983 до ~2018 годов (прогноз);
6-й цикл — с ~2018 до ~ 2060 (прогноз)^[11].

Однако имеются различия в датировке «посткондратьевских» циклов, например, также приводятся следующие границы начала и конца «посткондратьевских» волн^[12]:

3-й цикл: 1890—1896 — 1939—1950;
4-й цикл: 1939—1950 — 1984—1991;
5-й цикл: 1984—1991 — ?

Циклы Шмихулы

Циклы Шмихулы — долгосрочные циклы технологического прогресса, являющиеся частью долгосрочных экономических волн.^[1] Они являются ключевым понятием теории технологического прогресса Даниэля Шмихулы.

Содержание

1 Характеристика теории
2 Технологические революции
3 Критика теории
4 Примечания

Характеристика теории

Теория циклов технологических революций Даниэля Шхмиулы заключается в том, что главные технологические инновации происходят не постоянно, а посредством особых циклов, и временные интервалы этих циклов сокращаются из-за технического прогресса.^[2] ^[3] ^[4]

Период времени с наиболее высокой концентрацией технологических новшеств обозначается “технологической революцией”. Период технологической революции (этап инноваций) соотносится с фазой начала экономического роста. Когда появляются новые технологии, доказавшие свою пригодность на практике, происходит временное сокращение новых технологических разработок, так как в этот период делается упор на максимальное практическое применение уже существующих технологий. Этот период обозначается как этап применения. Этот этап связан с периодом экономического роста и, возможно, даже экономическим бумом. Однако в определенный момент прибыльность (соотношение прибыли и цены) новых технологий снижается до уровня технологий предыдущего поколения. Рынки насыщены технологическими продуктами, а новые капиталовложения в этот изначально новый сектор не принесут прибыли выше средней. В этот момент начинается кризис, который подталкивает к новым технологическим исследованиям. Таким образом, этап стагнации и кризис преодолеваются новой технологической революцией с новыми технологиями, которые оживят экономику.^[5] И эта новая технологическая революция - начало новой волны.^[6]

Внутренняя структура каждой длинной волны такова:

1) этап инноваций – технологическая революция (начало экономического роста после кризиса, конца предыдущей волны)

2) этап применения (экономический бум)

3) этап стагнации – насыщение экономики и общества инновациями (экономический кризис)

Технологические революции

Согласно теории Шмихулы, технологические революции являются главным двигателем экономического развития, и, следовательно, долгосрочные экономические циклы зависят от волн технологических инноваций^[7]. Шмихула определил шесть циклов технологических инноваций современной эпохи, начатых технологическими революциями (одна из них - гипотетическая революция в ближайшем будущем). Также, он выделил подобные циклы в предсовременной эпохе.

Технологические циклы предсовременной эпохи:

Цикл	Период	Технологическая революция	Наиболее важные инновации
1.	1900-1100 до н.э.	Индоевропейская технологическая революция	Коневодство, обработка железа
2.	700-200 до н.э	Кельтская и греческая технологическая революция	Железные инструменты и оружие, античная греческая цивилизация
3.	300-700 н.э.	Германо-славянская технологическая революция	Двухпольное система земледелия, использование тяжелого плуга, использования конских стремян
4.	930-1200	Средневековая технологическая революция	Трехпольная система земледелия, подковывание лошадей, водные и ветряные мельницы, удобрения
4.	1340-1470	Технологическая революция эпохи ренессанса	Огнестрельное оружие, доменная печь, книгопечатние подвижными литерами, часы, астролябия, компас, великие географические открытия

Технологические циклы современной эпохи:

Цикл	Период	Технологическая революция	Лидирующие сектора экономики
1.	1600–1740	Финансово-агрокультурная революция	Финансы, сельское хозяйство, торговля
2.	1780–1840	Индустриальная революция	Текстиль, железо, уголь, железные дороги, каналы
3.	1880–1920	Техническая революция	Химия, электротехническая промышленность, машиностроение
4.	1940–1970	Научно-техническая революция	Авиационная промышленность, ядерная промышленность, космонавтика, синтетические материалы, нефтяная промышленность, кибернетика

5.	1985–2000	Информационная и телекоммуникационная революция	Телекоммуникации, кибернетика, информатика, интернет
6.	2015-2025 (?)	Гипотетическая пост-информационная технологическая революция	Биомедицина, нанотехнологии, альтернативные виды топлива

Теория Шмихулы технологических революций популярна среди сторонников теории длинных экономических волн (например, циклов Кондратьева) и среди ученых, которые полагают, что экономический кризис в 2007-2012 годах был результатом технологического застоя^[8] ^[9] ^[10] ^[11].

Российский социолог А.А. Давыдов определил математическую формулу для определения длин циклов Шмихулы, которая основана на последовательности Фибоначчи^[12].

Критика теории

Данная теория имеет ту же проблему, что и другие теории длинного цикла - иногда её трудно обосновать точными данными, в связи с отсутствием необходимых и достаточных статистических данных, а потенциальная долгосрочная кривая всегда изменяется под влиянием других кратковременных или более масштабных факторов, поэтому ее курс всегда лишь довольно абстрактная реконструкция. Кроме того, идея концентрации наиболее важных нововведений в определенные периоды времени представляется логичной, но ее проверка зависит от весьма субъективного определения «наиболее важных» технологических инноваций. Теория циклов Шмихулы более популярна в России, Бразилии^[13] и Индии^[14], чем в Европе^[15]^[16].

Примечания

↑ Показывать компактно

1. ↑ Niels Posthumus: Financiële lente is nog ver weg (Trouw, 12/11/10)

2. ↑ Šmihula, Daniel (2009): The waves of the technological innovations of the modern age and the present crisis as the end of the wave of the informational technological revolution, Studia politica Slovaca, 1/2009, Bratislava, ISSN 1337-8163 , pp. 32-47 [1]

3. ↑ Šmihula, Daniel (2011): Long waves of technological innovations, Studia politica Slovaca, 2/2011, Bratislava, ISSN 1337-8163 , pp. 50-69 [2]

4. ↑ D.Šmihula: Informačná a komunikačná revolúcia sa stáva minulosťou, SLOVO, 2008 [3]

5. ↑ Brian Chan: Future of Product Design (2011)

6. ↑ Shipbuilding – Market Forecast

7. ↑ Halina Ward: „The Future of Democracy in the Face of Climate Change“, Foundation for Democracy and Sustainable Development (January 2012), p. 86 and 127

8. ↑ Smihula’s Modified Kondratiev-Wave Schema

9. ↑ Kondratieff Wave

10. ↑ Lewy Land: Kondratieff Waves... Crashed Our Economy!

11. ↑ Mag. Veronika Hornung-Prähauser, MAS: Systemic innovations enabled by information and communication technology in education (2011) [4]

12. ↑ А.А. Давыдов: ВОЛНЫ ИННОВАЦИЙ И ЧИСЛА ФИБОНАЧЧИ: ОЦЕНКА ПЕРСПЕКТИВНОСТИ ГИПОТЕЗЫ [5]

13. ↑ Ivan Barbosa da Cunha: RELATÓRIO E PARECER PRÉVIO DAS CONTAS ANUAIS DO GOVERNO DO ESTADO DO PARÁ EXERCÍCIO 2009 (2010)[6]

14. ↑ Dr. Prashant Wasankar: Riding the Bull

15. ↑ Enrico Tronchin: Disruptive innovation for sustained economic growth, Why New Zealand’s innovation system should be open, distributed and inclusive of innovative users (2011), in Proceedings of the International Conference on Invention, Innovation and Commercialisation with special emphasis on Technology Users Innovation (TUI), p.37 [7][8]

16. ↑ Simon Berkovich: Obtaining inexhaustible clean energy by parametric resonance under nonlocality clocking (2010) [9]

Содержание

1 Биография
2 Монографии
3 Научные статьи
4 Ссылки

Биография

Окончил факультет психологии МГУ им. М. В. Ломоносова (1981), кандидат социологических наук, доктор философских наук, профессор. Руководитель социологической службы управления «Главмосремонт» при Исполкоме Моссовета (1981—1985), младший научный сотрудник (1985), старший научный сотрудник Института социологии РАН (1992—1996), главный научный сотрудник Института социологии РАН (2000), эксперт ВЦИОМ и аналитического управления Администрации Президента РФ, преподаватель МГИМО МИД РФ, первый федеральный вице-президент РОС, руководитель Научно-исследовательского комитета «Системная социология» РОС (1989).

Основные направления научной деятельности: теория, моделирование и прогнозирование социальных систем, разработчик теории системной социологии и концепции нанообщества.

Действительный член Нью-Йоркской академии наук, член-корреспондент Международной академии информационных процессов и технологий.

Автор более 100 научных работ, из них 7 монографий.

Монографии

Давыдов А. А. Модульный анализ и конструирование социума. М.: ИС РАН, 1994.
Давыдов А. А., Чураков А. Н. Модульный анализ и моделирование социума. М.: ИС РАН, 2000.
Давыдов А. А. Системный подход в социологии: законы социальных систем. М.: Эдиториал УРСС, 2004.
Давыдов А. А. Системный подход в социологии: новые направления, теории и методы анализа социальных систем. М.: Эдиториал УРСС, 2005.
Давыдов А. А. Системная социология. М.: Эдиториал УРСС, 2006.
Давыдов А. А. Системная социология: введение в анализ динамики социума. М.: ЛКИ, 2007.
Давыдов А. А. Конкурентные преимущества системной социологии. М.: ИС РАН, 2008.

Числа Фибоначчи

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 ноября 2017; проверки требует 1 правка.

Чи́сла Фибона́ччи (также Фибона́чи^[1]) — элементы числовой последовательности

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (последовательность A000045 в OEIS),

в которой первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел. Названы в честь средневекового математика Леонардо Пизанского (известного как Фибоначчи)^[2].

Более формально, последовательность чисел Фибоначчи { F n } {\displaystyle \left\{F_{n}\right\}} задаётся линейным рекуррентным соотношением:

F 0 = 0 , F 1 = 1 , F n = F n − 1 + F n − 2 , n ⩾ 2 , n ∈ Z . {\displaystyle F_{0}=0,\qquad F_{1}=1,\qquad F_{n}=F_{n-1}+F_{n-2},\quad n\geqslant 2,\quad n\in \mathbb {Z} .}

Иногда числа Фибоначчи рассматривают и для отрицательных значений n {\displaystyle n} , как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. При этом члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: F n = F n + 2 − F n + 1 {\displaystyle F_{n}=F_{n+2}-F_{n+1}} :

n	…	−10	−9	−8	−7	−6	−5	−4	−3	−2	−1	0	1	2	3	4	5	6	7	8	9	10	…
F n {\displaystyle F_{n}}	…	−55	34	−21	13	−8	5	−3	2	−1	1	0	1	1	2	3	5	8	13	21	34	55	…

Легко заметить, что F − n = ( − 1 ) n + 1 F n {\displaystyle F_{-n}=(-1)^{n+1}F_{n}} .

Содержание

1 Происхождение
2 Формула Бине
3 Тождества
4 Свойства
5 Вариации и обобщения
6 В других областях

6.1 В природе

7 См. также
8 Примечания
9 Литература
10 Ссылки

Происхождение

Страница Книги абака (лат. Liber abaci) Фибоначчи из Национальной центральной библиотеки Флоренции.
В правом блоке демонстрируется последовательность Фибоначчи.
Позиции от 0 до 12 обозначены тёмным цветом римскими цифрами, а значения красным цветом индо-арабскими цифрами

Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении) намного раньше, чем стала известна в Европе.

Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».

На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая, что: изначально есть новорожденная пара кроликов (самец и самка); со второго месяца после своего рождения кролики начинают спариваться и каждый месяц производить новую пару кроликов; кролики никогда не умирают. Сколько пар кроликов будет через год?

В начале первого месяца есть только одна новорожденная пара (1).
В конце первого месяца по-прежнему только одна пара кроликов, но уже спарившаяся (1)
В конце второго месяца первая пара рождает новую пару и опять спаривается (2)
В конце третьего месяца первая пара рождает ещё одну новую пару и спаривается, вторая пара только спаривается (3)
В конце четвёртого месяца первая пара рождает ещё одну новую пару и спаривается, вторая пара рождает новую пару и спаривается, третья пара только спаривается (5)

В конце n {\displaystyle n} -го месяца количество пар кроликов будет равно количеству пар в предыдущем месяце плюс количество новорожденных пар, которых будет столько же, сколько пар было два месяца назад. Таким образом: F n = F n − 2 + F n − 1 . {\displaystyle F_{n}=F_{n-2}+F_{n-1}.}

Формула Бине

Формула Бине выражает в явном виде значение F n {\displaystyle F_{n}} как функцию от n:

F n = ( 1 + 5 2 ) n − ( 1 − 5 2 ) n 5 = φ n − ( − φ ) − n φ − ( − φ ) − 1 = φ n − ( − φ ) − n 2 φ − 1 , {\displaystyle F_{n}={\frac {\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}}{\sqrt {5}}}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{\varphi -(-\varphi )^{-1}}}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{2\varphi -1}},}

где φ = 1 + 5 2 {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}} — золотое сечение. При этом φ {\displaystyle \varphi } и ( − φ ) − 1 = 1 − φ {\displaystyle (-\varphi )^{-1}=1-\varphi } являются корнями характеристического уравнения x 2 − x − 1 = 0 {\displaystyle x^{2}-x-1=0} .

Из формулы Бине следует, что для всех n ⩾ 0 {\displaystyle n\geqslant 0} , F n {\displaystyle F_{n}} есть ближайшее к φ n 5 {\displaystyle {\frac {\varphi ^{n}}{\sqrt {5}}}} целое число, то есть F n = ⌊ φ n 5 ⌉ {\displaystyle F_{n}=\left\lfloor {\frac {\varphi ^{n}}{\sqrt {5}}}\right\rceil } . В частности, при n → ∞ {\displaystyle n\to \infty } справедлива асимптотика F n ∼ φ n 5 {\displaystyle F_{n}\sim {\frac {\varphi ^{n}}{\sqrt {5}}}} .

Формула Бине может быть аналитически продолжена следующим образом:

F z = 1 5 ( φ z − cos ⁡ π z φ z ) . {\displaystyle F_{z}={\frac {1}{\sqrt {5}}}\left(\varphi ^{z}-{\frac {\cos {\pi z}}{\varphi ^{z}}}\right).}

При этом соотношение F z + 2 = F z + 1 + F z {\displaystyle F_{z+2}=F_{z+1}+F_{z}} выполняется для любого комплексного числа z.

Тождества

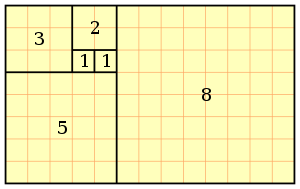
Иллюстрация формулы для суммы квадратов первых n чисел Фибоначчи^[3].

F 1 + F 2 + F 3 + ⋯ + F n = F n + 2 − 1 {\displaystyle F_{1}+F_{2}+F_{3}+\dots +F_{n}=F_{n+2}-1}
F 1 + F 3 + F 5 + ⋯ + F 2 n − 1 = F 2 n {\displaystyle F_{1}+F_{3}+F_{5}+\dots +F_{2n-1}=F_{2n}}
F 2 + F 4 + F 6 + ⋯ + F 2 n = F 2 n + 1 − 1 {\displaystyle F_{2}+F_{4}+F_{6}+\dots +F_{2n}=F_{2n+1}-1}
F n + 1 F n + 2 − F n F n + 3 = ( − 1 ) n {\displaystyle F_{n+1}F_{n+2}^{}-F_{n}F_{n+3}=(-1)^{n}}
F 1 2 + F 2 2 + F 3 2 + ⋯ + F n 2 = F n F n + 1 {\displaystyle F_{1}^{2}+F_{2}^{2}+F_{3}^{2}+\dots +F_{n}^{2}=F_{n}F_{n+1}} (см. рис.)
F n 2 + F n + 1 2 = F 2 n + 1 {\displaystyle F_{n}^{2}+F_{n+1}^{2}=F_{2n+1}}
F 2 n = F n + 1 2 − F n − 1 2 {\displaystyle F_{2n}=F_{n+1}^{2}-F_{n-1}^{2}}
F 3 n = F n + 1 3 + F n 3 − F n − 1 3 {\displaystyle F_{3n}=F_{n+1}^{3}+F_{n}^{3}-F_{n-1}^{3}}
F 5 n = 25 F n 5 + 25 ( − 1 ) n F n 3 + 5 F n {\displaystyle F_{5n}=25F_{n}^{5}+25(-1)^{n}F_{n}^{3}+5F_{n}}
F n + 1 = C n 0 + C n − 1 1 + C n − 2 2 + . . . {\displaystyle F_{n+1}=C_{n}^{0}+C_{n-1}^{1}+C_{n-2}^{2}+...}

И более общие формулы:

F n + m = F n − 1 F m + F n F m + 1 = F n + 1 F m + 1 − F n − 1 F m − 1 {\displaystyle F_{n+m}^{}=F_{n-1}F_{m}+F_{n}F_{m+1}=F_{n+1}F_{m+1}-F_{n-1}F_{m-1}}
F ( k + 1 ) n = F n − 1 F k n + F n F k n + 1 {\displaystyle F_{(k+1)n}^{}=F_{n-1}F_{kn}+F_{n}F_{kn+1}}
F n = F l F n − l + 1 + F l − 1 F n − l {\displaystyle F_{n}^{}=F_{l}F_{n-l+1}+F_{l-1}F_{n-l}}
Числа Фибоначчи представляются значениями континуант на наборе единиц: F n + 1 = K n ( 1 , … , 1 ) {\displaystyle F_{n+1}=K_{n}(1,\dots ,1)} , то есть

F n + 1 = det ( 1 1 0 ⋯ 0 − 1 1 1 ⋱ ⋮ 0 − 1 ⋱ ⋱ 0 ⋮ ⋱ ⋱ ⋱ 1 0 ⋯ 0 − 1 1 ) {\displaystyle F_{n+1}=\det {\begin{pmatrix}1&1&0&\cdots &0\\-1&1&1&\ddots &\vdots \\0&-1&\ddots &\ddots &0\\\vdots &\ddots &\ddots &\ddots &1\\0&\cdots &0&-1&1\end{pmatrix}}} , а также F n + 1 = det ( 1 i 0 ⋯ 0 i 1 i ⋱ ⋮ 0 i ⋱ ⋱ 0 ⋮ ⋱ ⋱ ⋱ i 0 ⋯ 0 i 1 ) {\displaystyle \ F_{n+1}=\det {\begin{pmatrix}1&i&0&\cdots &0\\i&1&i&\ddots &\vdots \\0&i&\ddots &\ddots &0\\\vdots &\ddots &\ddots &\ddots &i\\0&\cdots &0&i&1\end{pmatrix}}} ,

где матрицы имеют размер n × n {\displaystyle n\times n} , i — мнимая единица.

Числа Фибоначчи можно выразить через многочлены Чебышёва:

F n + 1 = ( − i ) n U n ( − i 2 ) , {\displaystyle F_{n+1}=(-i)^{n}U_{n}\left({\frac {-i}{2}}\right),}

F 2 n + 2 = U n ( 3 2 ) . {\displaystyle F_{2n+2}=U_{n}\left({\frac {3}{2}}\right).}

Для любого n,

( 1 1 1 0 ) n = ( F n + 1 F n F n F n − 1 ) . {\displaystyle {\begin{pmatrix}1&1\\1&0\end{pmatrix}}^{n}={\begin{pmatrix}F_{n+1}&F_{n}\\F_{n}&F_{n-1}\end{pmatrix}}.}

· Следствие. Подсчёт определителей даёт

( − 1 ) n = F n + 1 F n − 1 − F n 2 . {\displaystyle (-1)^{n}=F_{n+1}F_{n-1}-F_{n}^{2}.}

Рекуррентная формула для получения чисел Фибоначчи:

F n + 1 = F n + 5 F n 2 ± 4 2 {\displaystyle F_{n+1}={\frac {F_{n}+{\sqrt {5F_{n}^{2}\pm 4}}}{2}}}

Знак перед коэффициентом 4 выбирается так, чтобы корень извлекался нацело.

Свойства

Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, то есть ( F m , F n ) = F ( m , n ) {\displaystyle (F_{m},F_{n})=F_{(m,n)}} . Следствия:

F m {\displaystyle F_{m}} делится на F n {\displaystyle F_{n}} тогда и только тогда, когда m {\displaystyle m} делится на n {\displaystyle n} (за исключением n = 2 {\displaystyle n=2} ). В частности, F m {\displaystyle F_{m}} делится на F 3 = 2 {\displaystyle F_{3}=2} (то есть является чётным) только для m = 3 k {\displaystyle m=3k} ; F m {\displaystyle F_{m}} делится на F 4 = 3 {\displaystyle F_{4}=3} только для m = 4 k {\displaystyle m=4k} ; F m {\displaystyle F_{m}} делится на F 5 = 5 {\displaystyle F_{5}=5} только для m = 5 k {\displaystyle m=5k} и т. д.
F m {\displaystyle F_{m}} может быть простым только для простых m {\displaystyle m} (с единственным исключением m = 4 {\displaystyle m=4} ). Например, число F 13 = 233 {\displaystyle F_{13}=233} простое, и его индекс 13 также прост. Обратное не верно, наименьший контрпример — F 19 = 4181 = 37 ⋅ 113 {\displaystyle F_{19}=4181=37\cdot 113} . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.

Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен x 2 − x − 1 {\displaystyle x^{2}-x-1} имеет корни φ {\displaystyle \varphi } и − 1 φ {\displaystyle -{\frac {1}{\varphi }}} .
Отношения F n + 1 F n {\displaystyle {\frac {F_{n+1}}{F_{n}}}} являются подходящими дробями золотого сечения ϕ {\displaystyle \phi } и, в частности, lim n → ∞ F n + 1 F n = φ . {\displaystyle \lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}=\varphi .}
Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы

F n + 1 = ∑ k = 0 ⌊ n / 2 ⌋ ( n − k k ) {\displaystyle F_{n+1}=\sum _{k=0}^{\lfloor n/2\rfloor }{n-k \choose k}} .

В 1964 году Дж. Кон (J. H. E. Cohn) доказал,^[4] что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12:

F 0 = 0 2 = 0 {\displaystyle F_{0}=0^{2}=0} , F 1 = 1 2 = 1 {\displaystyle F_{1}=1^{2}=1} , F 2 = 1 2 = 1 {\displaystyle F_{2}=1^{2}=1} , F 12 = 12 2 = 144 {\displaystyle F_{12}=12^{2}=144} .

Производящей функцией последовательности чисел Фибоначчи является:

x + x 2 + 2 x 3 + 3 x 4 + 5 x 5 + ⋯ = ∑ n = 0 ∞ F n x n = x 1 − x − x 2 {\displaystyle x+x^{2}+2x^{3}+3x^{4}+5x^{5}+\dots =\sum _{n=0}^{\infty }F_{n}x^{n}={\frac {x}{1-x-x^{2}}}}

Множество чисел Фибоначчи совпадает с множеством неотрицательных значений многочлена

z ( x , y ) = 2 x y 4 + x 2 y 3 − 2 x 3 y 2 − y 5 − x 4 y + 2 y , {\displaystyle z(x,y)=2xy^{4}+x^{2}y^{3}-2x^{3}y^{2}-y^{5}-x^{4}y+2y,}

на множестве неотрицательных целых чисел x и y.^[5]

Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.

Период чисел Фибоначчи по модулю натурального числа n называется периодом Пизано и обозначается π(n). Периоды Пизано π(n) образуют последовательность:

1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175 в OEIS)

В частности, последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом π(10)=60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом π(100)=300, последние три цифры — с периодом π(1000)=1500, последние четыре — с периодом π(10000)=15000, последние пять — с периодом π(100000)=150000 и т. д.

Натуральное число N является числом Фибоначчи тогда и только тогда, когда 5 N 2 + 4 {\displaystyle 5N^{2}+4} или 5 N 2 − 4 {\displaystyle 5N^{2}-4} является квадратом.^[6]
Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи.^[7]
Число Фибоначчи F n + 2 = F n + 1 + F n {\displaystyle F_{n+2}=F_{n+1}+F_{n}} равно количеству кортежей длины n из нулей и единиц, в которых нет двух соседних единиц. При этом F n + 1 {\displaystyle F_{n+1}} равно количеству таких кортежей, начинающихся с нуля, а F n {\displaystyle F_{n}} — начинающихся с единицы.
Число 0,112358132134… (после запятой записаны подряд идущие числа Фибоначчи) является иррациональным.^[^{источник не указан 1289 дней}^]

Вариации и обобщения

Числа трибоначчи
Числа Фибоначчи являются частным случаем последовательностей Люка F n = U n ( 1 , − 1 ) {\displaystyle F_{n}=U_{n}(1,-1)} .

При этом их дополнением являются числа Люка L n = V n ( 1 , − 1 ) {\displaystyle L_{n}=V_{n}(1,-1)} .

В других областях

Существует мнение, что почти все утверждения, находящие числа Фибоначчи в природных и исторических явлениях, неверны — это распространённый миф, который часто оказывается неточной подгонкой под желаемый результат^[8]^[9].

В природе

Филлотаксис (листорасположение) у растений описывается последовательностью Фибоначчи. Семена подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса также располагаются согласно последовательности Фибоначчи^[10]^[11]^[12]^[13]
Длины фаланг пальцев человека относятся примерно как числа Фибоначчи^[10]^[14].
Раковины моллюсков, в частности Наутилуса, строятся по спирали, соотносящейся^[^как?^] с рядом чисел Фибоначчи.^[^{источник не указан 557 дней}^]

См. также

Дерево Фибоначчи
Метод Фибоначчи с запаздываниями
Метод Фибоначчи поиска экстремума
Фибоначчи
Фибоначчиева система счисления
Числа Леонардо
Таблица Витхоффа
Последовательность коров Нараяны

Примечания

↑ Т. В. Кропотова, В. Г. Подольский, П. Е. Кашаргин. ВВЕДЕНИЕ В ВЫСШУЮ МАТЕМАТИКУ. Казанский федеральный университет институт физики
↑ Числа Фибоначчи // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.

↑ Фибоначчи числа // Энциклопедический словарь юного математика / Сост. Савин А. П.. — 2-е изд. — М.: Педагогика, 1989. — С. 312—314. — 352 с. — ISBN 5715502187.
↑ J H E Cohn. Square Fibonacci Numbers Etc, стр. 109–113.
↑ P. Ribenboim. The New Book of Prime Number Records. — Springer, 1996. — С. 193.
↑ Ira Gessel Problem H-187 // Fibonacci Quarterly. — 1972. — Т. 10. — С. 417–419.
↑ В. Серпинский . Задача 66 // 250 задач по элементарной теории чисел. — М.: Просвещение, 1968. — 168 с.
↑ Fibonacci Flim-Flam (англ.)
↑ The Myth That Will Not Go Away (англ.)

.Золотое сечение в природе
↑ Числа Фибоначчи
↑ Числа Фибоначчи
↑ Акимов О. Е. Конец науки.
↑ Г. Манукян. Поэзия чисел Фибоначчи

Литература

Н. Н. Воробьёв. Числа Фибоначчи. — Наука, 1978. — Т. 39. — (Популярные лекции по математике).
А. И. Маркушевич. Возвратные последовательности. — Гос. Издательство Технико-Теоретической Литературы, 1950. — Т. 1. — (Популярные лекции по математике).
А. Н. Рудаков Числа Фибоначчи и простота числа 2¹²⁷-1 // Математическое Просвещение, третья серия. — 2000. — Т. 4.
Дональд Кнут . Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4.
Дональд Кнут , Роналд Грэхем , Орен Паташник . Конкретная математика. Основание информатики = Concrete Mathematics. A Foundation for Computer Science. — М.: Мир; Бином. Лаборатория знаний, 2006. — С. 703. — ISBN 5-94774-560-7.
ГрантАракелян. Математика и история золотого сечения. — М.: Логос, 2014. — С. 404. — ISBN 978-5-98704-663-0.

Дерево Фибоначчи

Материал из Википедии — свободной энциклопедии

Стабильная версия была проверена 21 февраля 2017. Имеются непроверенные изменения в шаблонах или файлах.

В этой статье не хватает ссылок на источники информации . Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 21 февраля 2017 года.

Дерево Фибоначчи — АВЛ-дерево с наименьшим числом вершин при заданной высоте (глубине).

Если для какой-либо из вершин высота поддерева, для которого эта вершина является корнем, равна h {\displaystyle h} , то правое и левое поддерево этой вершины имеют высоты равные соответственно h − 1 {\displaystyle h-1} и h − 2 {\displaystyle h-2} , или h − 2 {\displaystyle h-2} и h − 1 {\displaystyle h-1} . Каждое поддерево дерева Фибоначчи также является деревом Фибоначчи.
Пустое дерево — дерево Фибоначчи высоты 0.
Дерево с одной вершиной — дерево Фибоначчи высоты 1.

Число вершин

Одно из весьма существенных свойств дерева Фибоначчи — количество вершин в нём может принимать только некоторый набор значений. Пусть N h {\displaystyle N_{h}} — число вершин в дереве Фибоначчи с высотой h {\displaystyle h} , тогда N 0 = 0 {\displaystyle N_{0}=0} , N 1 = 1 {\displaystyle N_{1}=1} , а для произвольного h число вершин можно описать рекуррентно: N h = N h − 1 + N h − 2 + 1 {\displaystyle N_{h}=N_{h-1}+N_{h-2}+1} . Дерево Фибоначчи названо так из-за схожести приведённой формулы с рекуррентным соотношением, определяющим последовательность чисел Фибоначчи. Для высоты h {\displaystyle h} число вершин N h = Φ h + 2 − 1 {\displaystyle N_{h}=\Phi _{h+2}-1} , где Φ n {\displaystyle \Phi _{n}} — n {\displaystyle n} -ое число Фибоначчи.

См. также

Дерево

Двоичное дерево

Двоичное дерево поиска

АВЛ-дерево

Числа Фибоначчи
Фибоначчи

Дерево (структура данных)

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 июня 2017; проверки требуют 2 правки.

У этого термина существуют и другие значения, см. Дерево (значения).

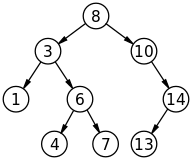
Простой пример дерева

Дерево — одна из наиболее широко распространённых структур данных в информатике, эмулирующая древовидную структуру в виде набора связанных узлов. Является связным графом, не содержащим циклы. Большинство источников также добавляют условие на то, что рёбра графа не должны быть ориентированными. В дополнение к этим трём ограничениям, в некоторых источниках указывается, что рёбра графа не должны быть взвешенными.

Содержание

1 Определения
2 Узлы

2.1 Корневые узлы

3 Поддеревья
4 Упорядочивание деревьев
5 Представление деревьев

5.1 Деревья как графы

6 Методы обхода
7 Общие операции
8 Общее применение
9 См. также
10 Примечания
11 Литература
12 Ссылки

Определения

Корневой узел — самый верхний узел дерева (узел 8 на примере).
Корень — одна из вершин, по желанию наблюдателя.

лист, листовой или терминальный узел — узел, не имеющий дочерних элементов (узлы 1, 4, 7, 13).

Внутренний узел — любой узел дерева, имеющий потомков, и таким образом, не являющийся листовым узлом (3, 6, 10, 14).

Дерево считается ориентированным, если в корень не заходит ни одно ребро.

Полный сцепленный ключ — идентификатор записи, который образуется путём конкатенации всех ключей экземпляров родительских записей (групп).

Узлы

Узел является экземпляром одного из двух типов элементов графа, соответствующим объекту некоторой фиксированной природы. Узел может содержать значение, состояние или представление отдельной информационной структуры или самого дерева. Каждый узел дерева имеет ноль или более узлов-потомков, которые располагаются ниже по дереву (по соглашению, деревья 'растут' вниз, а не вверх, как это происходит с настоящими деревьями). Узел, имеющий потомка, называется узлом-родителем относительно своего потомка (или узлом-предшественником, или старшим). Каждый узел имеет не больше одного предка. Высота узла — это максимальная длина нисходящего пути от этого узла к самому нижнему узлу (краевому узлу), называемому листом. Высота корневого узла равна высоте всего дерева. Глубина вложенности узла равна длине пути до корневого узла.

Корневые узлы

Узел, не имеющий предков (самый верхний), называется корневым узлом. Это узел, на котором начинается выполнение большинства операций над деревом (хотя некоторые алгоритмы начинают выполнение с «листов» и выполняются, пока не достигнут корня). Все прочие узлы могут быть достигнуты путём перехода от корневого узла по рёбрам (или ссылкам). (Согласно формальному определению, каждый подобный путь должен быть уникальным). В диаграммах он обычно изображается на самой вершине. В некоторых деревьях, например, кучах, корневой узел обладает особыми свойствами. Каждый узел дерева можно рассматривать как корневой узел поддерева, «растущего» из этого узла.

Поддеревья

Поддерево — часть древообразной структуры данных, которая может быть представлена в виде отдельного дерева. Любой узел дерева T вместе со всеми его узлами-потомками является поддеревом дерева T. Для любого узла поддерева либо должен быть путь в корневой узел этого поддерева, либо сам узел должен являться корневым. То есть поддерево связано с корневым узлом целым деревом, а отношения поддерева со всеми прочими узлами определяются через понятие соответствующее поддерево (по аналогии с термином «соответствующее подмножество»).

Упорядочивание деревьев

Существует два основных типа деревьев. В рекурсивном дереве или неупорядоченном дереве имеет значение лишь структура самого дерева без учёта порядка потомков для каждого узла. Дерево, в котором задан порядок (например, каждому ребру, ведущему к потомку, присвоены различные натуральные числа) называется деревом с именованными рёбрами или упорядоченным деревом со структурой данных, заданной перед именованием и называемой структурой данных упорядоченного дерева.

Упорядоченные деревья являются наиболее распространёнными среди древовидных структур. Двоичное дерево поиска — одно из разновидностей упорядоченного дерева.

Представление деревьев

Существует множество различных способов представления деревьев. Наиболее общий способ представления изображает узлы как записи, расположенные в динамически выделяемой памяти с указателями на своих потомков, предков (или и тех и других), или как элементы массива, связанные между собой отношениями, определёнными их позициями в массиве (например, двоичная куча).

Деревья как графы

В теории графов дерево — связный ациклический граф. Корневое дерево — это граф с вершиной, выделенной в качестве корневой. В этом случае любые две вершины, связанные ребром, наследуют отношения «родитель-потомок». Несвязный граф, состоящий исключительно из деревьев, называется лесом.

Методы обхода

Основная статья: Обход дерева

Пошаговый перебор элементов дерева по связям между узлами-предками и узлами-потомками называется обходом дерева. Зачастую операция может быть выполнена переходом указателя по отдельным узлам. Обход, при котором каждый узел-предок просматривается прежде его потомков, называется предупорядоченным обходом или обходом в прямом порядке (pre-order walk), а когда просматриваются сначала потомки, а потом предки, то обход называется поступорядоченным обходом или обходом в обратном порядке (post-order walk). Существует также симметричный обход, при котором посещается сначала левое поддерево, затем узел, затем — правое поддерево, и обход в ширину, при котором узлы посещаются уровень за уровнем (N-й уровень дерева — множество узлов с высотой N). Каждый уровень обходится слева направо.

Общие операции

вставка нового элемента в определённую позицию;
вставка поддерева;
добавление ветви дерева (называется прививкой);
нахождение корневого элемента для любого узла;
нахождение наименьшего общего предка двух вершин;
перебор всех элементов дерева;
перебор элементов ветви дерева;
поиск изоморфного поддерева;
поиск элемента;
удаление ветви дерева (называется обрезкой);
удаление поддерева;
удаление элемента.

Общее применение

управление иерархией данных;
упрощение поиска информации (см. обход дерева);
управление сортированными списками данных;
синтаксический разбор арифметических выражений (англ. parsing), оптимизация программ;
в качестве технологии компоновки цифровых картинок для получения различных визуальных эффектов;
форма принятия многоэтапного решения (см. деловые шахматы).

См. также

Двоичное разбиение пространства
Куча (структура данных)
Дерево (теория графов)
Дерево (теория наборов)
Древовидная структура
Префиксное дерево
Экспоненциальное дерево

Распространённые древовидные структуры

Двоичное дерево

Самобалансирующиеся двоичные деревья поиска

АА-дерево
АВЛ-дерево
Красно-чёрное дерево
Расширяющееся дерево
Дерево со штрафами

Прочие деревья

B-дерево (2-3-дерево, B+-деревья, B*-дерево, UB-дерево)
DSW-алгоритм
Танцующее дерево
Анфилада
Смешанное дерево
k-мерное дерево
Октодерево
Квадродерево
R-дерево (структура_данных)
Дерево покрытий
Дерево остатков
Сегментное дерево
Список с пропусками
T-дерево
T-пирамида
Верхнее дерево
Дерево ван Емде Боаса
Список структур данных (деревья)

Примечания

Литература

Дональд Э. Кнут . Глава 2.3. Деревья // Искусство программирования = The Art of Computer Programming. — 3-е изд. — М.: Вильямс, 2000. — Т. 2. Основные алгоритмы. — 832 с. — 7000 экз. — ISBN 5-8459-0081-6 (рус.) ISBN 0-201-89684-2 (англ.).
Томас Кормен , Чарльз Лейзерсон , Рональд Ривест , Клиффорд Штайн . Introduction to Algorithms. — 2nd Edition. — MIT Press, McGraw-Hill, 2001. — ISBN 0-262-03293-7.

Section 10.4: Representing rooted trees, pp.214-217.
Chapters 12-14 (Binary Search Trees, Red-Black Trees, Augmenting Data Structures), pp. 253—320.

Ссылки

Описание из Словаря алгоритмов и структур данных
Описание древовидных структур
Обходы бинарных деревьев
Красно-черные деревья

АВЛ-дерево

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 декабря 2015; проверки требуют 11 правок.

Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей.

АВЛ-дерево

Тип

дерево поиска

Изобретено в

1962 году

Изобретено

Адельсон-Вельский Георгий Максимович и Ландис Евгений Михайлович

Временная сложность
в О-символике

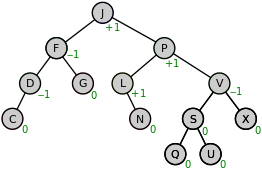
В среднем В худшем случае Расход памяти O(n) O(n) Поиск O(log n) O(log n) Вставка O(log n) O(log n) Удаление O(log n) O(log n)

АВЛ-дерево — сбалансированное по высоте двоичное дерево поиска: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.

АВЛ — аббревиатура, образованная первыми буквами фамилий создателей (советских учёных) Адельсон-Вельского Георгия Максимовича и Ландиса Евгения Михайловича.

Содержание

1 Максимальная высота
2 Балансировка
3 Алгоритм добавления вершины
4 Алгоритм удаления вершины
5 Нерекурсивная вставка в АВЛ-дерево сверху-вниз
6 Нерекурсивное удаление из АВЛ-дерева сверху вниз
7 Расстановка балансов при удалении
8 Расстановка балансов при одинарном повороте
9 Расстановка балансов при двойном повороте
10 Оценка эффективности
11 См. также
12 Примечания
13 Литература

Максимальная высота

Максимальная высота АВЛ-дерева при заданном числе узлов ^[1]:

h ≤ ⌊ 1.45 log 2 ⁡ ( n + 2 ) ⌋ {\displaystyle h\;\leq \;\lfloor 1.45\log _{2}(n+2)\rfloor \;}

Количество возможных высот на практике сильно ограничено (при 32-битной адресации максимальная высота равна 45, при 48-битной — 68), поэтому лучше заранее подсчитать все возможные значения минимального количества узлов для каждой высоты с помощью рекуррентной формулы для дерева Фибоначчи:

n 0 = 0 {\displaystyle n_{0}=0} ,

n 1 = 1 {\displaystyle n_{1}=1} ,

n h = n h − 2 + n h − 1 + 1 {\displaystyle n_{h}=n_{h-2}+n_{h-1}+1} .

Промежуточные значения количества узлов будут соответствовать предыдущей (меньшей) высоте.

Балансировка

Относительно АВЛ-дерева балансировкой вершины называется операция, которая в случае разницы высот левого и правого поддеревьев = 2, изменяет связи предок-потомок в поддереве данной вершины так, что разница становится <= 1, иначе ничего не меняет. Указанный результат получается вращениями поддерева данной вершины.

Используются 4 типа вращений:

Малое левое вращение		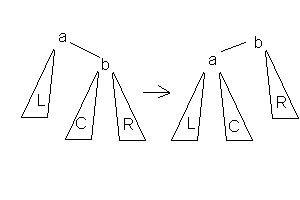Данное вращение используется тогда, когда высота b-поддерева — высота L = 2 и высота С <= высота R.
Большое левое вращение		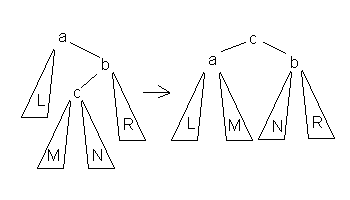Данное вращение используется тогда, когда высота b-поддерева — высота L = 2 и высота c-поддерева > высота R.
Малое правое вращение		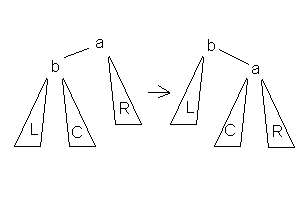Данное вращение используется тогда, когда высота b-поддерева — высота R = 2 и высота С <= высота L.
Большое правое вращение		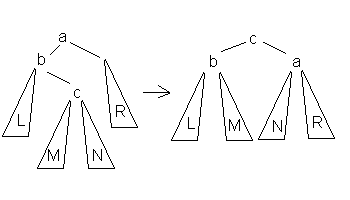Данное вращение используется тогда, когда высота b-поддерева — высота R = 2 и высота c-поддерева > высота L.

В каждом случае достаточно просто доказать то, что операция приводит к нужному результату и что полная высота уменьшается не более чем на 1 и не может увеличиться. Также можно заметить, что большое левое вращение это композиция правого малого вращения и левого малого вращения. Из-за условия балансированности высота дерева О(log(N)), где N- количество вершин, поэтому добавление элемента требует O(log(N)) операций.

Алгоритм добавления вершины

Показатель сбалансированности в дальнейшем будем интерпретировать как разность между высотой левого и правого поддерева, а алгоритм будет основываться на типе TAVLTree, описанном выше. Непосредственно при вставке (листу) присваивается нулевой баланс. Процесс включения вершины состоит из трех частей (данный процесс описан Никлаусом Виртом в «Алгоритмы и структуры данных»):

Прохода по пути поиска, пока не убедимся, что ключа в дереве нет.
Включения новой вершины в дерево и определения результирующих показателей балансировки.
«Отступления» назад по пути поиска и проверки в каждой вершине показателя сбалансированности. Если необходимо — балансировка.

Будем возвращать в качестве результата функции, уменьшилась высота дерева или нет. Предположим, что процесс из левой ветви возвращается к родителю (рекурсия идет назад), тогда возможны три случая: { h_l — высота левого поддерева, h_r — высота правого поддерева } Включение вершины в левое поддерево приведет к

h_l < h_r: выравняется h_l = h_r. Ничего делать не нужно.
h_l = h_r: теперь левое поддерево будет больше на единицу, но балансировка пока не требуется.
h_l > h_r: теперь h_l — h_r = 2, — требуется балансировка.

В третьей ситуации требуется определить балансировку левого поддерева. Если левое поддерево этой вершины (Tree^.left^.left) выше правого (Tree^.left^.right), то требуется большое правое вращение, иначе хватит малого правого. Аналогичные (симметричные) рассуждения можно привести и для включение в правое поддерево.

Алгоритм удаления вершины

Для простоты опишем рекурсивный алгоритм удаления. Если вершина — лист, то удалим её и вызовем балансировку всех её предков в порядке от родителя к корню. Иначе найдём самую близкую по значению вершину в поддереве наибольшей высоты (правом или левом) и переместим её на место удаляемой вершины, при этом вызвав процедуру её удаления.

Докажем, что данный алгоритм сохраняет балансировку. Для этого докажем по индукции по высоте дерева, что после удаления некоторой вершины из дерева и последующей балансировки высота дерева уменьшается не более, чем на 1. База индукции: Для листа очевидно верно. Шаг индукции: Либо условие балансированности в корне (после удаления корень может изменится) не нарушилось, тогда высота данного дерева не изменилась, либо уменьшилось строго меньшее из поддеревьев => высота до балансировки не изменилась => после уменьшится не более чем на 1.

Очевидно, что в результате указанных действий процедура удаления вызывается не более 3 раз, так как у вершины, удаляемой по второму вызову, нет одного из поддеревьев. Но поиск ближайшего каждый раз требует O(N) операций. Становится очевидной возможность оптимизации: поиск ближайшей вершины может быть выполнен по краю поддерева, что сокращает сложность до O(log(N)).

Оценка эффективности

Из формулы, приведённой выше, высота АВЛ-дерева никогда не превысит высоту идеально сбалансированного дерева более, чем на 45%. Для больших n {\displaystyle n} имеет место оценка 1.04 log 2 ⁡ n {\displaystyle 1.04\log _{2}{n}} . Таким образом, выполнение основных операций требует порядка log 2 ⁡ n {\displaystyle \log _{2}{n}} сравнений. Экспериментально выяснено, что одна балансировка приходится на каждые 2 включения и на каждые 5 исключений.

См. также

Сбалансированные (самобалансирующиеся) деревья:

Красно-чёрное дерево
Матричное дерево
Идеально сбалансированное дерево
Расширяющееся дерево
Список структур данных (деревья)

Расширяющееся дерево

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 сентября 2016; проверки требуют 2 правки.

Расширяющееся дерево

Тип

Дерево

Изобретено в

1985 году

Изобретено

Дэниел Слитор и Роберт Андре Тарьян

Временная сложность
в О-символике

В среднем В худшем случае Расход памяти O(n) O(n) Поиск O(log n) O(log n) Вставка O(log n) O(log n) Удаление O(log n) O(log n)

Расширяющееся (англ. splay tree) или косое дерево является двоичным деревом поиска, в котором поддерживается свойство сбалансированности. Это дерево принадлежит классу «саморегулирующихся деревьев», которые поддерживают необходимый баланс ветвления дерева, чтобы обеспечить выполнение операций поиска, добавления и удаления за логарифмическое время от числа хранимых элементов. Это реализуется без использования каких-либо дополнительных полей в узлах дерева (как, например, в Красно-чёрных деревьях или АВЛ-деревьях, где в вершинах хранится, соответственно, цвет вершины и глубина поддерева). Вместо этого «расширяющие операции» (splay operation), частью которых являются вращения, выполняются при каждом обращении к дереву.

Учётная стоимость (англ.) в расчёте на одну операцию с деревом составляет O ( log ⁡ n ) {\displaystyle O(\log n)} .

Расширяющееся дерево придумали Роберт Тарьян и Даниель Слейтор в 1983 году.

Содержание

1 Операции

1.1 Splay (расширение)
1.2 Search (поиск элемента)
1.3 Insert (добавление элемента)
1.4 Delete (удаление элемента)
1.5 Merge (объединение двух деревьев)
1.6 Split (разделение дерева на две части)

2 Реализация
3 Примечание
4 См. также
5 Литература

Операции

В другом языковом разделе есть более полная статья Splay tree (англ.) Вы можете помочь проекту, расширив текущую статью с помощью перевода. При этом, для соблюдения правил атрибуции, следует установить шаблон {{Переведённая статья}} на страницу обсуждения, либо указать ссылку на статью-источник в комментарии к правке.

Splay (расширение)

Основная операция дерева. Заключается в перемещении вершины в корень при помощи последовательного выполнения трёх операций: Zig, Zig-Zig и Zig-Zag. Обозначим вершину, которую хотим переместить в корень за x, её родителя — p, а родителя p (если существует) — g.

Zig: выполняется, когда p является корнем. Дерево поворачивается по ребру между x и p. Существует лишь для разбора крайнего случая и выполняется только один раз в конце, когда изначальная глубина x была нечётна.

Zig-Zig: выполняется, когда и x, и p являются левыми (или правыми) сыновьями. Дерево поворачивается по ребру между g и p, а потом — по ребру между p и x.

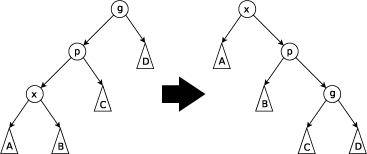
Zig-Zag: выполняется, когда x является правым сыном, а p — левым (или наоборот). Дерево поворачивается по ребру между p и x, а затем — по ребру между x и g.

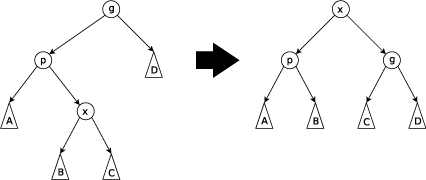
Search (поиск элемента)

Поиск выполняется как в обычном двоичном дереве поиска. При нахождении элемента запускаем Splay для него.

Insert (добавление элемента)

Вставка происходит как в обычном бинарном дереве поиска, после, запускаем Split() от добавляемого элемента и подвешиваем получившиеся деревья за него.

Delete (удаление элемента)

Находим элемент в дереве, делаем Splay для него, делаем текущим деревом Merge его детей.

Merge (объединение двух деревьев)

Для слияния деревьев T1 и T2, в которых все ключи T1 меньше ключей в T2, делаем Splay для максимального элемента T1, тогда у корня T1 не будет правого ребенка. После этого делаем T2 правым ребенком T1.

Реализация

Одной из реализаций расширяющегося дерева может послужить реализация, использующая 3 указателя в каждой вершине: указатель на правого и левого сыновей, а также на родителя. Это позволяет избежать рекурсивной реализации, что, в свою очередь, повлечет экономию памяти. Минусом в данном случае выступает большее количество присваиваний для обновления указателей, что может сказаться на конечной производительности.

Ниже представлена реализация расширяющегося дерева, использующая по 3 указателя в каждом узле. Также, в данной реализации операция Splay используется во всех основных операциях, выполняемых над деревом - при вставке, удалении и поиске для достижения лучшей сбалансированности дерева.

#ifndef SPLAYTREE_H#define SPLAYTREE_H template<typename T> class SplayTree {private: struct SplayNode { Node * leftChild; Node * rightChild Node * parent; T data; Node (const T & key = T()) : leftChild(nullptr), rightChild(nullptr), parent(nullptr), key(key) {} ~Node () { if (leftChild) delete leftChild; if (rightChild) delete rightChild; if (parent) delete parent; } } * root; private: SplayNode * _Successor(SplayNode * localRoot) const { SplayNode * successor = localRoot; if (successor->rightChild != nullptr) { successor = _Minimum(successor->rightChild); } else { while (successor != successor->parent->leftChild || successor != root) { successor = successor->parent; } } return successor; } SplayNode * _Predecessor(SplayNode * localRoot) const { SplayNode * predecessor = localRoot; if (predecessor->leftChild != nullptr) { predecessor = _Maximum(predecessor->leftChild); } else { while (predecessor != predecessor->parent->rightChild || predecessor != root) { predecessor = predecessor->parent; } } return predecessor; } SplayNode * _Minimum(SplayNode * localRoot) const { SplayNode * minimum = localRoot; while (minimum != nullptr) minimum = minimum->leftChild; return minimum; } SplayNode * _Maximum(SplayNode * localRoot) const { SplayNode * maximum = localRoot; while (maximum != nullptr) maximum = maximum->rightChild; return maximum; } SplayNode * _Search(const T & key) { SplayNode * searchedElement = root; while (searchedElement != nullptr) { if (searchedElement->data < key) searchedElement = searchedElement->rightChild; else if (key < searchedElement->data) searchedElement = searchedElement->leftChild; else if (searchedElement->data == key) { _Splay(searchedElement); return searchedElement; } } return nullptr; } void _LeftRotate(SplayNode * localRoot) { SplayNode * rightChild = localRoot->rightChild; localRoot->rightChild = rightChild->leftChild; if (rightChild->leftChild != nullptr) rightChild->leftChild->parent = localRoot; _Transplant(localRoot, rightChild); rightChild->leftChild = localRoot; rightChild->leftChild->parent = rightChild; } void _RightRotate(SplayNode * localRoot) { SplayNode * leftChild = localRoot->leftChild; localRoot->leftChild = leftChild->rightChild; if (leftChild->rightChild != nullptr) leftChild->rightChild->parent = localRoot; _Transplant(localRoot, leftChild); leftChild->rightChild = localRoot; leftChild->rightChild->parent = leftChild; } void _Transplant(SplayNode * localParent, SplayNode * localChild) { if (localParent->parent == nullptr) root = localChild; else if (localParent == localParent->parent->leftChild) localParent->parent->leftChild = localChild; else if (localParent == localParent->parent->rightChild) localParent->parent->rightChild = localChild; if (localChild != nullptr) localChild->parent = localParent->parent; } void _Splay(SplayNode * pivotElement) { while (pivotElement != root) { if (pivotElement->parent == root) { if (pivotElement == pivotElement->parent->leftChild) _RightRotate(pivotElement); else if (pivotElement == pivotElement->parent->rightChild) { _LeftRotate(pivotElement); } else { // Zig-Zig step. if (pivotElement == pivotElement->parent->leftChild && pivotElement->parent == pivotElement->parent->parent->leftChild) { _RightRotate(pivotElement->parent->parent); _RightRotate(pivotElement->parent); } else if (pivotElement == pivotElement->parent->rightChild && pivotElement->parent == pivotElement->parent->parent->rightChild) { _LeftRotate(pivotElement->parent->parent); _LeftRotate(pivotElement->parent); } // Zig-Zag step. else if (pivotElement == pivotElement->parent->rightChild && pivotElement->parent == pivotElement->parent->parent->leftChild) { _LeftRotate(pivotElement->parent); _RightRotate(pivotElement->parent->parent); } else if (pivotElement == pivotElement->parent->leftChild && pivotElement->parent == pivotElement->parent->parent->rightChild) { _RightRotate(pivotElement->parent); _LeftRotate(pivotElement->parent->parent); } } } } public: SplayTree() { root = nullptr; } virtual ~SplayTree() { delete root; } void Insert(const T & key) { SplayNode * preInsertPlace = nullptr; SplayNode * insertPlace = root; while (insertPlace != nullptr) { preInsertPlace = insertPlace; if (insertPlace->data() < key) insertPlace = insertPlace->rightChild; else if (key < insertPlace->data) { insertPlace = insertPlace->leftChild; } SplayNode * insertElement = new SplayNode(key); insertElement->parent = preInsertPlace; if (preInsertPlace == nullptr) root = insertElement; else if (preInsertPlace->data < insertElement->data) preInsertPlace->rightChild = insertElement; else if (insertElement->data < preInsertPlace->data) preInsertPlace->leftChild = insertElement; _Splay(insertElement); } void Remove(const T & key) { SplayNode * removeElement = _Search(key); if (removeElement != nullptr) { if (removeElement->rightChild == nullptr) _Transplant(removeElement, removeElement->leftChild); else if (removeElement->leftChild == nullptr) _Transplant(removeElement, removeElement->leftChild); else { SplayNode * newLocalRoot = _Minimum(removeElement->rightChild); if (newLocalRoot->parent != removeElement) { _Transplant(newLocalRoot, newLocalRoot->rightChild); newLocalRoot->rightChild = removeElement->rightChild; newLocalRoot->rightChild->parent = newLocalRoot; } _Transplant(removeElement, newLocalRoot); newLocalRoot->leftChild = removeElement->leftChild; newLocalRoot->leftChild->parent = newLocalRoot; _Splay(newLocalRoot); } delete removeElement; } } bool Search(const T &key) { return _Search(key) != nullptr; } bool isEmpty() const { return root == nullptr; } T Successor(const T & key) { if (_Successor(_Search(key)) != nullptr) { return _Successor(_Search(key))->getValue(); } else { return -1; } } T Predecessor(const T & key) { if (_Predecessor(_Search(key)) != nullptr) { return _Predecessor(_Search(key))->getValue(); } else { return -1; } }}; #endif //SPLAYTREE_H

Примечание

Расширяющееся дерево предоставляет самоизменяющуюся структуру — структуру, характеризующуюся тенденцией хранить узлы, к которым часто происходит обращение, вблизи верхушки дерева, в то время как узлы к которым обращение происходит редко перемещаются ближе к листьям. Таким образом время обращения к часто посещаемым узлам будет меньше, а время обращения к редко посещаемым узлам — больше среднего.

Расширяющееся дерево не обладает никакими явными функциями балансировки, но процесс скоса узлов к корню способствует поддержанию дерева в сбалансированном виде.

См. также

Сбалансированные (самобалансирующиеся) деревья:

· Красно-чёрное дерево

· Матричное дерево

· АВЛ-дерево

· Идеально сбалансированное дерево

Список структур данных (деревья)

Литература

Томас Х. Кормен и др. Алгоритмы: построение и анализ. — 2-е изд. — М.: Издательский дом «Вильямс», 2007. — С. 1296. — ISBN 5-8459-0857-4.
Daniel Sleator, Robert Tarjan. A data structure for dynamic trees. — Journal of Computer and System Sciences, 1983. — С. 262-391.

Экономические циклы

ЦИКЛЫ КИТЧИНА

Циклы Жюгляра

В своей работе Жюгляр приводит следующие значения данных о кризисах во Франции, Британии и США^[3]:

1803—1804
1810—1810
1813—1815—1814
1818—1818—1818
1826—1826—1826
1830—1830—1830
1836—1837—1837
1839—1839—1839
1847—1847—1848
1857—1857—1857

Фазы цикла Жюгляра

В цикле Жюгляра достаточно часто выделяют четыре фазы, в которых некоторые исследователи выделяют подфазы:

фаза оживления (подфазы старта и ускорения);
фаза подъёма, или процветания (подфазы роста и перегрева, или бума) ;
фаза рецессии (подфазы краха/острого кризиса и спада);
фаза депрессии, или застоя (подфазы стабилизации и сдвига)^[4].

Фазы подъёма (пика) и депрессии (дна) традиционно совпадают с экстремумом подфаз - циклов Китчена.

3. Ритмы Кузнеца

Материал из Википедии — свободной энциклопедии

1815
1836
1853
1873
1882
1892
1907
1920
1929

Циклы Кондратьева

Содержание

1 История
2 Концепция
3 Датировки волн
4 Соотношение с технологическими укладами
5 Примечания
6 Литература
7 Ссылки

История

Концепция

Датировки волн

Для периода после промышленной революции обычно выделяются следующие кондратьевские волны:

1-й цикл — с 1803 до 1841—1843 годов (отмечены моменты минимумов экономических показателей мировой экономики);
2-й цикл — с 1844—1851 до 1890—1896 годов;
3-й цикл — с 1891—1896 до 1945—1947 годов;
4-й цикл — с 1945—1947 до 1981—1983 годов;
5-й цикл — с 1981—1983 до ~2018 годов (прогноз);
6-й цикл — с ~2018 до ~ 2060 (прогноз)^[11].

3-й цикл: 1890—1896 — 1939—1950;
4-й цикл: 1939—1950 — 1984—1991;
5-й цикл: 1984—1991 — ?

Соотношение с технологическими укладами

Основная статья: Технологический уклад

Многие исследователи связывают смену волн с технологическими укладами. Прорывные технологии открывают возможности для расширения производства и формируют новые секторы экономики, образующие новый технологический уклад. Кроме того, кондратьевские волны являются одной из важнейших форм реализации индустриальных принципов производства^[13].

Сводная система кондратьевских волн и соответствующих им технологических укладов выглядит следующим образом:

1-й цикл — текстильные фабрики, промышленное использование каменного угля;
2-й цикл — угледобыча и чёрная металлургия, железнодорожное строительство, паровой двигатель;
3-й цикл — тяжёлое машиностроение, электроэнергетика, неорганическая химия, производство стали и электрических двигателей;
4-й цикл — производство автомобилей и других машин, химическая промышленность, нефтепереработка и двигатели внутреннего сгорания, массовое производство;
5-й цикл — развитие электроники, робототехники, вычислительной, лазерной и телекоммуникационной техники;
6-й цикл — возможно, NBIC-конвергенция (конвергенция нано-, био-, информационных и когнитивных технологий)^[14].

Даниэль Шмихула (Daniel Šmihula) в работе «The waves of the technological innovations of the modern age and the present crisis as the end of the wave of the informational technological revolution» (2009) считает, что к началу 21 века циклы данного типа сократились по времени с 60 до 30 или даже 20 лет из-за постоянного ускорения развития технологий^[15] (см. Циклы Шмихулы).

Циклы Шмихулы

Содержание

1 Характеристика теории
2 Технологические революции
3 Критика теории
4 Примечания

Характеристика теории

Внутренняя структура каждой длинной волны такова:

2) этап применения (экономический бум)

3) этап стагнации – насыщение экономики и общества инновациями (экономический кризис)

Технологические революции

Технологические циклы предсовременной эпохи:

Цикл	Период	Технологическая революция	Наиболее важные инновации
1.	1900-1100 до н.э.	Индоевропейская технологическая революция	Коневодство, обработка железа
2.	700-200 до н.э	Кельтская и греческая технологическая революция	Железные инструменты и оружие, античная греческая цивилизация
3.	300-700 н.э.	Германо-славянская технологическая революция	Двухпольное система земледелия, использование тяжелого плуга, использования конских стремян
4.	930-1200	Средневековая технологическая революция	Трехпольная система земледелия, подковывание лошадей, водные и ветряные мельницы, удобрения
4.	1340-1470	Технологическая революция эпохи ренессанса	Огнестрельное оружие, доменная печь, книгопечатние подвижными литерами, часы, астролябия, компас, великие географические открытия

Технологические циклы современной эпохи:

Цикл	Период	Технологическая революция	Лидирующие сектора экономики
1.	1600–1740	Финансово-агрокультурная революция	Финансы, сельское хозяйство, торговля
2.	1780–1840	Индустриальная революция	Текстиль, железо, уголь, железные дороги, каналы
3.	1880–1920	Техническая революция	Химия, электротехническая промышленность, машиностроение
4.	1940–1970	Научно-техническая революция	Авиационная промышленность, ядерная промышленность, космонавтика, синтетические материалы, нефтяная промышленность, кибернетика

5.	1985–2000	Информационная и телекоммуникационная революция	Телекоммуникации, кибернетика, информатика, интернет
6.	2015-2025 (?)	Гипотетическая пост-информационная технологическая революция	Биомедицина, нанотехнологии, альтернативные виды топлива

Критика теории

Примечания

↑ Показывать компактно

1. ↑ Niels Posthumus: Financiële lente is nog ver weg (Trouw, 12/11/10)

3. ↑ Šmihula, Daniel (2011): Long waves of technological innovations, Studia politica Slovaca, 2/2011, Bratislava, ISSN 1337-8163 , pp. 50-69 [2]

4. ↑ D.Šmihula: Informačná a komunikačná revolúcia sa stáva minulosťou, SLOVO, 2008 [3]

5. ↑ Brian Chan: Future of Product Design (2011)

6. ↑ Shipbuilding – Market Forecast

7. ↑ Halina Ward: „The Future of Democracy in the Face of Climate Change“, Foundation for Democracy and Sustainable Development (January 2012), p. 86 and 127

8. ↑ Smihula’s Modified Kondratiev-Wave Schema

9. ↑ Kondratieff Wave

10. ↑ Lewy Land: Kondratieff Waves... Crashed Our Economy!

11. ↑ Mag. Veronika Hornung-Prähauser, MAS: Systemic innovations enabled by information and communication technology in education (2011) [4]

12. ↑ А.А. Давыдов: ВОЛНЫ ИННОВАЦИЙ И ЧИСЛА ФИБОНАЧЧИ: ОЦЕНКА ПЕРСПЕКТИВНОСТИ ГИПОТЕЗЫ [5]

13. ↑ Ivan Barbosa da Cunha: RELATÓRIO E PARECER PRÉVIO DAS CONTAS ANUAIS DO GOVERNO DO ESTADO DO PARÁ EXERCÍCIO 2009 (2010)[6]

14. ↑ Dr. Prashant Wasankar: Riding the Bull

16. ↑ Simon Berkovich: Obtaining inexhaustible clean energy by parametric resonance under nonlocality clocking (2010) [9]

Дата: 2018-12-28, просмотров: 363.

12 3 4 Следующая ⇒