Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Материал из Википедии — свободной энциклопедии

В Википедии есть статьи о других людях с такой фамилией, см. Давыдов; Давыдов, Андрей.

Андрей Александрович Давыдов

Дата рождения: 29 декабря 1954 (62 года) Место рождения: Москва Страна:

• СССР
• Россия

Научная сфера: социология Место работы: Институт социологии РАН Альма-матер : МГУ им. М. В. Ломоносова Учёная степень: доктор философских наук]] кандидат социологических наук Учёное звание: профессор Известен как: специалист в области системной социологии и нанообщества Награды и премии: Финалист I Всемирного конкурса работ молодых социологов (Испания, Мадрид, 1990)

Андре́й Алекса́ндрович Давы́дов (род. 29 декабря 1954, Москва) — российский социолог.

Содержание

• 1 Биография
• 2 Монографии
• 3 Научные статьи
• 4 Ссылки

Биография

Окончил факультет психологии МГУ им. М. В. Ломоносова (1981), кандидат социологических наук, доктор философских наук, профессор. Руководитель социологической службы управления «Главмосремонт» при Исполкоме Моссовета (1981—1985), младший научный сотрудник (1985), старший научный сотрудник Института социологии РАН (1992—1996), главный научный сотрудник Института социологии РАН (2000), эксперт ВЦИОМ и аналитического управления Администрации Президента РФ, преподаватель МГИМО МИД РФ, первый федеральный вице-президент РОС, руководитель Научно-исследовательского комитета «Системная социология» РОС (1989).

Основные направления научной деятельности: теория, моделирование и прогнозирование социальных систем, разработчик теории системной социологии и концепции нанообщества.

Действительный член Нью-Йоркской академии наук, член-корреспондент Международной академии информационных процессов и технологий.

Автор более 100 научных работ, из них 7 монографий.

Монографии

• Давыдов А. А. Модульный анализ и конструирование социума. М.: ИС РАН, 1994.
• Давыдов А. А., Чураков А. Н. Модульный анализ и моделирование социума. М.: ИС РАН, 2000.
• Давыдов А. А. Системный подход в социологии: законы социальных систем. М.: Эдиториал УРСС, 2004.
• Давыдов А. А. Системный подход в социологии: новые направления, теории и методы анализа социальных систем. М.: Эдиториал УРСС, 2005.
• Давыдов А. А. Системная социология. М.: Эдиториал УРСС, 2006.
• Давыдов А. А. Системная социология: введение в анализ динамики социума. М.: ЛКИ, 2007.
• Давыдов А. А. Конкурентные преимущества системной социологии. М.: ИС РАН, 2008.

Числа Фибоначчи

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 ноября 2017; проверки требует 1 правка.

Чи́сла Фибона́ччи (также Фибона́чи^[1]) — элементы числовой последовательности

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (последовательность A000045 в OEIS),

в которой первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел. Названы в честь средневекового математика Леонардо Пизанского (известного как Фибоначчи)^[2].

Более формально, последовательность чисел Фибоначчи { F n } {\displaystyle \left\{F_{n}\right\}} задаётся линейным рекуррентным соотношением:

F 0 = 0 , F 1 = 1 , F n = F n − 1 + F n − 2 , n ⩾ 2 , n ∈ Z . {\displaystyle F_{0}=0,\qquad F_{1}=1,\qquad F_{n}=F_{n-1}+F_{n-2},\quad n\geqslant 2,\quad n\in \mathbb {Z} .}

Иногда числа Фибоначчи рассматривают и для отрицательных значений n {\displaystyle n} , как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. При этом члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: F n = F n + 2 − F n + 1 {\displaystyle F_{n}=F_{n+2}-F_{n+1}} :

n	…	−10	−9	−8	−7	−6	−5	−4	−3	−2	−1	0	1	2	3	4	5	6	7	8	9	10	…
F n {\displaystyle F_{n}}	…	−55	34	−21	13	−8	5	−3	2	−1	1	0	1	1	2	3	5	8	13	21	34	55	…

Легко заметить, что F − n = ( − 1 ) n + 1 F n {\displaystyle F_{-n}=(-1)^{n+1}F_{n}} .

Содержание

• 1 Происхождение
• 2 Формула Бине
• 3 Тождества
• 4 Свойства
• 5 Вариации и обобщения
• 6 В других областях
• 6.1 В природе
• 7 См. также
• 8 Примечания
• 9 Литература
• 10 Ссылки

Происхождение

Страница Книги абака (лат. Liber abaci) Фибоначчи из Национальной центральной библиотеки Флоренции.
В правом блоке демонстрируется последовательность Фибоначчи.
Позиции от 0 до 12 обозначены тёмным цветом римскими цифрами, а значения красным цветом индо-арабскими цифрами

Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении) намного раньше, чем стала известна в Европе.

Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».

На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая, что: изначально есть новорожденная пара кроликов (самец и самка); со второго месяца после своего рождения кролики начинают спариваться и каждый месяц производить новую пару кроликов; кролики никогда не умирают. Сколько пар кроликов будет через год?

• В начале первого месяца есть только одна новорожденная пара (1).
• В конце первого месяца по-прежнему только одна пара кроликов, но уже спарившаяся (1)
• В конце второго месяца первая пара рождает новую пару и опять спаривается (2)
• В конце третьего месяца первая пара рождает ещё одну новую пару и спаривается, вторая пара только спаривается (3)
• В конце четвёртого месяца первая пара рождает ещё одну новую пару и спаривается, вторая пара рождает новую пару и спаривается, третья пара только спаривается (5)

В конце n {\displaystyle n} -го месяца количество пар кроликов будет равно количеству пар в предыдущем месяце плюс количество новорожденных пар, которых будет столько же, сколько пар было два месяца назад. Таким образом: F n = F n − 2 + F n − 1 . {\displaystyle F_{n}=F_{n-2}+F_{n-1}.}

Формула Бине

Формула Бине выражает в явном виде значение F n {\displaystyle F_{n}} как функцию от n:

F n = ( 1 + 5 2 ) n − ( 1 − 5 2 ) n 5 = φ n − ( − φ ) − n φ − ( − φ ) − 1 = φ n − ( − φ ) − n 2 φ − 1 , {\displaystyle F_{n}={\frac {\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}}{\sqrt {5}}}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{\varphi -(-\varphi )^{-1}}}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{2\varphi -1}},}

где φ = 1 + 5 2 {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}} — золотое сечение. При этом φ {\displaystyle \varphi } и ( − φ ) − 1 = 1 − φ {\displaystyle (-\varphi )^{-1}=1-\varphi } являются корнями характеристического уравнения x 2 − x − 1 = 0 {\displaystyle x^{2}-x-1=0} .

Из формулы Бине следует, что для всех n ⩾ 0 {\displaystyle n\geqslant 0} , F n {\displaystyle F_{n}} есть ближайшее к φ n 5 {\displaystyle {\frac {\varphi ^{n}}{\sqrt {5}}}} целое число, то есть F n = ⌊ φ n 5 ⌉ {\displaystyle F_{n}=\left\lfloor {\frac {\varphi ^{n}}{\sqrt {5}}}\right\rceil } . В частности, при n → ∞ {\displaystyle n\to \infty } справедлива асимптотика F n ∼ φ n 5 {\displaystyle F_{n}\sim {\frac {\varphi ^{n}}{\sqrt {5}}}} .

Формула Бине может быть аналитически продолжена следующим образом:

F z = 1 5 ( φ z − cos ⁡ π z φ z ) . {\displaystyle F_{z}={\frac {1}{\sqrt {5}}}\left(\varphi ^{z}-{\frac {\cos {\pi z}}{\varphi ^{z}}}\right).}

При этом соотношение F z + 2 = F z + 1 + F z {\displaystyle F_{z+2}=F_{z+1}+F_{z}} выполняется для любого комплексного числа z.

Тождества

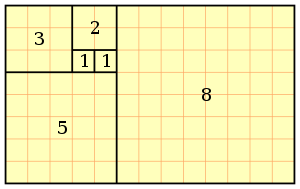
Иллюстрация формулы для суммы квадратов первых n чисел Фибоначчи^[3].

• F 1 + F 2 + F 3 + ⋯ + F n = F n + 2 − 1 {\displaystyle F_{1}+F_{2}+F_{3}+\dots +F_{n}=F_{n+2}-1}
• F 1 + F 3 + F 5 + ⋯ + F 2 n − 1 = F 2 n {\displaystyle F_{1}+F_{3}+F_{5}+\dots +F_{2n-1}=F_{2n}}
• F 2 + F 4 + F 6 + ⋯ + F 2 n = F 2 n + 1 − 1 {\displaystyle F_{2}+F_{4}+F_{6}+\dots +F_{2n}=F_{2n+1}-1}
• F n + 1 F n + 2 − F n F n + 3 = ( − 1 ) n {\displaystyle F_{n+1}F_{n+2}^{}-F_{n}F_{n+3}=(-1)^{n}}
• F 1 2 + F 2 2 + F 3 2 + ⋯ + F n 2 = F n F n + 1 {\displaystyle F_{1}^{2}+F_{2}^{2}+F_{3}^{2}+\dots +F_{n}^{2}=F_{n}F_{n+1}} (см. рис.)
• F n 2 + F n + 1 2 = F 2 n + 1 {\displaystyle F_{n}^{2}+F_{n+1}^{2}=F_{2n+1}}
• F 2 n = F n + 1 2 − F n − 1 2 {\displaystyle F_{2n}=F_{n+1}^{2}-F_{n-1}^{2}}
• F 3 n = F n + 1 3 + F n 3 − F n − 1 3 {\displaystyle F_{3n}=F_{n+1}^{3}+F_{n}^{3}-F_{n-1}^{3}}
• F 5 n = 25 F n 5 + 25 ( − 1 ) n F n 3 + 5 F n {\displaystyle F_{5n}=25F_{n}^{5}+25(-1)^{n}F_{n}^{3}+5F_{n}}
• F n + 1 = C n 0 + C n − 1 1 + C n − 2 2 + . . . {\displaystyle F_{n+1}=C_{n}^{0}+C_{n-1}^{1}+C_{n-2}^{2}+...}

И более общие формулы:

• F n + m = F n − 1 F m + F n F m + 1 = F n + 1 F m + 1 − F n − 1 F m − 1 {\displaystyle F_{n+m}^{}=F_{n-1}F_{m}+F_{n}F_{m+1}=F_{n+1}F_{m+1}-F_{n-1}F_{m-1}}
• F ( k + 1 ) n = F n − 1 F k n + F n F k n + 1 {\displaystyle F_{(k+1)n}^{}=F_{n-1}F_{kn}+F_{n}F_{kn+1}}
• F n = F l F n − l + 1 + F l − 1 F n − l {\displaystyle F_{n}^{}=F_{l}F_{n-l+1}+F_{l-1}F_{n-l}}
• Числа Фибоначчи представляются значениями континуант на наборе единиц: F n + 1 = K n ( 1 , … , 1 ) {\displaystyle F_{n+1}=K_{n}(1,\dots ,1)} , то есть

F n + 1 = det ( 1 1 0 ⋯ 0 − 1 1 1 ⋱ ⋮ 0 − 1 ⋱ ⋱ 0 ⋮ ⋱ ⋱ ⋱ 1 0 ⋯ 0 − 1 1 ) {\displaystyle F_{n+1}=\det {\begin{pmatrix}1&1&0&\cdots &0\\-1&1&1&\ddots &\vdots \\0&-1&\ddots &\ddots &0\\\vdots &\ddots &\ddots &\ddots &1\\0&\cdots &0&-1&1\end{pmatrix}}} , а также F n + 1 = det ( 1 i 0 ⋯ 0 i 1 i ⋱ ⋮ 0 i ⋱ ⋱ 0 ⋮ ⋱ ⋱ ⋱ i 0 ⋯ 0 i 1 ) {\displaystyle \ F_{n+1}=\det {\begin{pmatrix}1&i&0&\cdots &0\\i&1&i&\ddots &\vdots \\0&i&\ddots &\ddots &0\\\vdots &\ddots &\ddots &\ddots &i\\0&\cdots &0&i&1\end{pmatrix}}} ,

где матрицы имеют размер n × n {\displaystyle n\times n} , i — мнимая единица.

• Числа Фибоначчи можно выразить через многочлены Чебышёва:

F n + 1 = ( − i ) n U n ( − i 2 ) , {\displaystyle F_{n+1}=(-i)^{n}U_{n}\left({\frac {-i}{2}}\right),}

F 2 n + 2 = U n ( 3 2 ) . {\displaystyle F_{2n+2}=U_{n}\left({\frac {3}{2}}\right).}

• Для любого n,

( 1 1 1 0 ) n = ( F n + 1 F n F n F n − 1 ) . {\displaystyle {\begin{pmatrix}1&1\\1&0\end{pmatrix}}^{n}={\begin{pmatrix}F_{n+1}&F_{n}\\F_{n}&F_{n-1}\end{pmatrix}}.}

· Следствие. Подсчёт определителей даёт

( − 1 ) n = F n + 1 F n − 1 − F n 2 . {\displaystyle (-1)^{n}=F_{n+1}F_{n-1}-F_{n}^{2}.}

• Рекуррентная формула для получения чисел Фибоначчи:

F n + 1 = F n + 5 F n 2 ± 4 2 {\displaystyle F_{n+1}={\frac {F_{n}+{\sqrt {5F_{n}^{2}\pm 4}}}{2}}}

Знак перед коэффициентом 4 выбирается так, чтобы корень извлекался нацело.

Свойства

• Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, то есть ( F m , F n ) = F ( m , n ) {\displaystyle (F_{m},F_{n})=F_{(m,n)}} . Следствия:
• F m {\displaystyle F_{m}} делится на F n {\displaystyle F_{n}} тогда и только тогда, когда m {\displaystyle m} делится на n {\displaystyle n} (за исключением n = 2 {\displaystyle n=2} ). В частности, F m {\displaystyle F_{m}} делится на F 3 = 2 {\displaystyle F_{3}=2} (то есть является чётным) только для m = 3 k {\displaystyle m=3k} ; F m {\displaystyle F_{m}} делится на F 4 = 3 {\displaystyle F_{4}=3} только для m = 4 k {\displaystyle m=4k} ; F m {\displaystyle F_{m}} делится на F 5 = 5 {\displaystyle F_{5}=5} только для m = 5 k {\displaystyle m=5k} и т. д.
• F m {\displaystyle F_{m}} может быть простым только для простых m {\displaystyle m} (с единственным исключением m = 4 {\displaystyle m=4} ). Например, число F 13 = 233 {\displaystyle F_{13}=233} простое, и его индекс 13 также прост. Обратное не верно, наименьший контрпример — F 19 = 4181 = 37 ⋅ 113 {\displaystyle F_{19}=4181=37\cdot 113} . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.

• Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен x 2 − x − 1 {\displaystyle x^{2}-x-1} имеет корни φ {\displaystyle \varphi } и − 1 φ {\displaystyle -{\frac {1}{\varphi }}} .
• Отношения F n + 1 F n {\displaystyle {\frac {F_{n+1}}{F_{n}}}} являются подходящими дробями золотого сечения ϕ {\displaystyle \phi } и, в частности, lim n → ∞ F n + 1 F n = φ . {\displaystyle \lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}=\varphi .}
• Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы

F n + 1 = ∑ k = 0 ⌊ n / 2 ⌋ ( n − k k ) {\displaystyle F_{n+1}=\sum _{k=0}^{\lfloor n/2\rfloor }{n-k \choose k}} .

• В 1964 году Дж. Кон (J. H. E. Cohn) доказал,^[4] что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12:

F 0 = 0 2 = 0 {\displaystyle F_{0}=0^{2}=0} , F 1 = 1 2 = 1 {\displaystyle F_{1}=1^{2}=1} , F 2 = 1 2 = 1 {\displaystyle F_{2}=1^{2}=1} , F 12 = 12 2 = 144 {\displaystyle F_{12}=12^{2}=144} .

• Производящей функцией последовательности чисел Фибоначчи является:

x + x 2 + 2 x 3 + 3 x 4 + 5 x 5 + ⋯ = ∑ n = 0 ∞ F n x n = x 1 − x − x 2 {\displaystyle x+x^{2}+2x^{3}+3x^{4}+5x^{5}+\dots =\sum _{n=0}^{\infty }F_{n}x^{n}={\frac {x}{1-x-x^{2}}}}

• Множество чисел Фибоначчи совпадает с множеством неотрицательных значений многочлена

z ( x , y ) = 2 x y 4 + x 2 y 3 − 2 x 3 y 2 − y 5 − x 4 y + 2 y , {\displaystyle z(x,y)=2xy^{4}+x^{2}y^{3}-2x^{3}y^{2}-y^{5}-x^{4}y+2y,}

на множестве неотрицательных целых чисел x и y.^[5]

• Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.

• Период чисел Фибоначчи по модулю натурального числа n называется периодом Пизано и обозначается π(n). Периоды Пизано π(n) образуют последовательность:

1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175 в OEIS)

• В частности, последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом π(10)=60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом π(100)=300, последние три цифры — с периодом π(1000)=1500, последние четыре — с периодом π(10000)=15000, последние пять — с периодом π(100000)=150000 и т. д.
• Натуральное число N является числом Фибоначчи тогда и только тогда, когда 5 N 2 + 4 {\displaystyle 5N^{2}+4} или 5 N 2 − 4 {\displaystyle 5N^{2}-4} является квадратом.^[6]
• Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи.^[7]
• Число Фибоначчи F n + 2 = F n + 1 + F n {\displaystyle F_{n+2}=F_{n+1}+F_{n}} равно количеству кортежей длины n из нулей и единиц, в которых нет двух соседних единиц. При этом F n + 1 {\displaystyle F_{n+1}} равно количеству таких кортежей, начинающихся с нуля, а F n {\displaystyle F_{n}} — начинающихся с единицы.
• Число 0,112358132134… (после запятой записаны подряд идущие числа Фибоначчи) является иррациональным.^{[источник не указан 1289 дней]}

Вариации и обобщения

• Числа трибоначчи
• Числа Фибоначчи являются частным случаем последовательностей Люка F n = U n ( 1 , − 1 ) {\displaystyle F_{n}=U_{n}(1,-1)} .
• При этом их дополнением являются числа Люка L n = V n ( 1 , − 1 ) {\displaystyle L_{n}=V_{n}(1,-1)} .

В других областях

Существует мнение, что почти все утверждения, находящие числа Фибоначчи в природных и исторических явлениях, неверны — это распространённый миф, который часто оказывается неточной подгонкой под желаемый результат^[8][9].

В природе

• Филлотаксис (листорасположение) у растений описывается последовательностью Фибоначчи. Семена подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса также располагаются согласно последовательности Фибоначчи^{[10][11][12][13]}
• Длины фаланг пальцев человека относятся примерно как числа Фибоначчи^[10][14].
• Раковины моллюсков, в частности Наутилуса, строятся по спирали, соотносящейся^[как?] с рядом чисел Фибоначчи.^{[источник не указан 557 дней]}

См. также

• Дерево Фибоначчи
• Метод Фибоначчи с запаздываниями
• Метод Фибоначчи поиска экстремума
• Фибоначчи
• Фибоначчиева система счисления
• Числа Леонардо
• Таблица Витхоффа
• Последовательность коров Нараяны

Примечания

1. ↑ Т. В. Кропотова, В. Г. Подольский, П. Е. Кашаргин. ВВЕДЕНИЕ В ВЫСШУЮ МАТЕМАТИКУ. Казанский федеральный университет институт физики
2. ↑ Числа Фибоначчи // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.

 

 

1. ↑ Фибоначчи числа // Энциклопедический словарь юного математика / Сост. Савин А. П.. — 2-е изд. — М.: Педагогика, 1989. — С. 312—314. — 352 с. — ISBN 5715502187.
2. ↑ J H E Cohn. Square Fibonacci Numbers Etc, стр. 109–113.
3. ↑ P. Ribenboim. The New Book of Prime Number Records. — Springer, 1996. — С. 193.
4. ↑ Ira Gessel Problem H-187 // Fibonacci Quarterly. — 1972. — Т. 10. — С. 417–419.
5. ↑ В. Серпинский . Задача 66 // 250 задач по элементарной теории чисел. — М.: Просвещение, 1968. — 168 с.
6. ↑ Fibonacci Flim-Flam (англ.)
7. ↑ The Myth That Will Not Go Away (англ.)

1. .Золотое сечение в природе
2. ↑ Числа Фибоначчи
3. ↑ Числа Фибоначчи
4. ↑ Акимов О. Е. Конец науки.
5. ↑ Г. Манукян. Поэзия чисел Фибоначчи

Литература

• Н. Н. Воробьёв. Числа Фибоначчи. — Наука, 1978. — Т. 39. — (Популярные лекции по математике).
• А. И. Маркушевич. Возвратные последовательности. — Гос. Издательство Технико-Теоретической Литературы, 1950. — Т. 1. — (Популярные лекции по математике).
• А. Н. Рудаков Числа Фибоначчи и простота числа 2¹²⁷-1 // Математическое Просвещение, третья серия. — 2000. — Т. 4.
• Дональд Кнут . Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4.
• Дональд Кнут , Роналд Грэхем , Орен Паташник . Конкретная математика. Основание информатики = Concrete Mathematics. A Foundation for Computer Science. — М.: Мир; Бином. Лаборатория знаний, 2006. — С. 703. — ISBN 5-94774-560-7.
• ГрантАракелян. Математика и история золотого сечения. — М.: Логос, 2014. — С. 404. — ISBN 978-5-98704-663-0.

Дерево Фибоначчи

Материал из Википедии — свободной энциклопедии

Стабильная версия была проверена 21 февраля 2017. Имеются непроверенные изменения в шаблонах или файлах.

В этой статье не хватает ссылок на источники информации . Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 21 февраля 2017 года.

Дерево Фибоначчи — АВЛ-дерево с наименьшим числом вершин при заданной высоте (глубине).

1. Если для какой-либо из вершин высота поддерева, для которого эта вершина является корнем, равна h {\displaystyle h} , то правое и левое поддерево этой вершины имеют высоты равные соответственно h − 1 {\displaystyle h-1} и h − 2 {\displaystyle h-2} , или h − 2 {\displaystyle h-2} и h − 1 {\displaystyle h-1} . Каждое поддерево дерева Фибоначчи также является деревом Фибоначчи.
2. Пустое дерево — дерево Фибоначчи высоты 0.
3. Дерево с одной вершиной — дерево Фибоначчи высоты 1.

Число вершин

Одно из весьма существенных свойств дерева Фибоначчи — количество вершин в нём может принимать только некоторый набор значений. Пусть N h {\displaystyle N_{h}} — число вершин в дереве Фибоначчи с высотой h {\displaystyle h} , тогда N 0 = 0 {\displaystyle N_{0}=0} , N 1 = 1 {\displaystyle N_{1}=1} , а для произвольного h число вершин можно описать рекуррентно: N h = N h − 1 + N h − 2 + 1 {\displaystyle N_{h}=N_{h-1}+N_{h-2}+1} . Дерево Фибоначчи названо так из-за схожести приведённой формулы с рекуррентным соотношением, определяющим последовательность чисел Фибоначчи. Для высоты h {\displaystyle h} число вершин N h = Φ h + 2 − 1 {\displaystyle N_{h}=\Phi _{h+2}-1} , где Φ n {\displaystyle \Phi _{n}} — n {\displaystyle n} -ое число Фибоначчи.

См. также

• Дерево
• Двоичное дерево
• Двоичное дерево поиска
• АВЛ-дерево
• Числа Фибоначчи
• Фибоначчи

Дерево (структура данных)

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 июня 2017; проверки требуют 2 правки.

У этого термина существуют и другие значения, см. Дерево (значения).

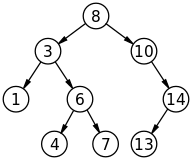
Простой пример дерева

Дерево — одна из наиболее широко распространённых структур данных в информатике, эмулирующая древовидную структуру в виде набора связанных узлов. Является связным графом, не содержащим циклы. Большинство источников также добавляют условие на то, что рёбра графа не должны быть ориентированными. В дополнение к этим трём ограничениям, в некоторых источниках указывается, что рёбра графа не должны быть взвешенными.

Содержание

• 1 Определения
• 2 Узлы
• 2.1 Корневые узлы
• 3 Поддеревья
• 4 Упорядочивание деревьев
• 5 Представление деревьев
• 5.1 Деревья как графы
• 6 Методы обхода
• 7 Общие операции
• 8 Общее применение
• 9 См. также
• 10 Примечания
• 11 Литература
• 12 Ссылки

Определения

• Корневой узел — самый верхний узел дерева (узел 8 на примере).
• Корень — одна из вершин, по желанию наблюдателя.

• лист, листовой или терминальный узел — узел, не имеющий дочерних элементов (узлы 1, 4, 7, 13).

• Внутренний узел — любой узел дерева, имеющий потомков, и таким образом, не являющийся листовым узлом (3, 6, 10, 14).

Дерево считается ориентированным, если в корень не заходит ни одно ребро.

• Полный сцепленный ключ — идентификатор записи, который образуется путём конкатенации всех ключей экземпляров родительских записей (групп).

Узлы

Узел является экземпляром одного из двух типов элементов графа, соответствующим объекту некоторой фиксированной природы. Узел может содержать значение, состояние или представление отдельной информационной структуры или самого дерева. Каждый узел дерева имеет ноль или более узлов-потомков, которые располагаются ниже по дереву (по соглашению, деревья 'растут' вниз, а не вверх, как это происходит с настоящими деревьями). Узел, имеющий потомка, называется узлом-родителем относительно своего потомка (или узлом-предшественником, или старшим). Каждый узел имеет не больше одного предка. Высота узла — это максимальная длина нисходящего пути от этого узла к самому нижнему узлу (краевому узлу), называемому листом. Высота корневого узла равна высоте всего дерева. Глубина вложенности узла равна длине пути до корневого узла.

Корневые узлы

Узел, не имеющий предков (самый верхний), называется корневым узлом. Это узел, на котором начинается выполнение большинства операций над деревом (хотя некоторые алгоритмы начинают выполнение с «листов» и выполняются, пока не достигнут корня). Все прочие узлы могут быть достигнуты путём перехода от корневого узла по рёбрам (или ссылкам). (Согласно формальному определению, каждый подобный путь должен быть уникальным). В диаграммах он обычно изображается на самой вершине. В некоторых деревьях, например, кучах, корневой узел обладает особыми свойствами. Каждый узел дерева можно рассматривать как корневой узел поддерева, «растущего» из этого узла.

Поддеревья

Поддерево — часть древообразной структуры данных, которая может быть представлена в виде отдельного дерева. Любой узел дерева T вместе со всеми его узлами-потомками является поддеревом дерева T. Для любого узла поддерева либо должен быть путь в корневой узел этого поддерева, либо сам узел должен являться корневым. То есть поддерево связано с корневым узлом целым деревом, а отношения поддерева со всеми прочими узлами определяются через понятие соответствующее поддерево (по аналогии с термином «соответствующее подмножество»).

Упорядочивание деревьев

Существует два основных типа деревьев. В рекурсивном дереве или неупорядоченном дереве имеет значение лишь структура самого дерева без учёта порядка потомков для каждого узла. Дерево, в котором задан порядок (например, каждому ребру, ведущему к потомку, присвоены различные натуральные числа) называется деревом с именованными рёбрами или упорядоченным деревом со структурой данных, заданной перед именованием и называемой структурой данных упорядоченного дерева.

Упорядоченные деревья являются наиболее распространёнными среди древовидных структур. Двоичное дерево поиска — одно из разновидностей упорядоченного дерева.

Представление деревьев

Существует множество различных способов представления деревьев. Наиболее общий способ представления изображает узлы как записи, расположенные в динамически выделяемой памяти с указателями на своих потомков, предков (или и тех и других), или как элементы массива, связанные между собой отношениями, определёнными их позициями в массиве (например, двоичная куча).

Деревья как графы

В теории графов дерево — связный ациклический граф. Корневое дерево — это граф с вершиной, выделенной в качестве корневой. В этом случае любые две вершины, связанные ребром, наследуют отношения «родитель-потомок». Несвязный граф, состоящий исключительно из деревьев, называется лесом.

Методы обхода

Основная статья: Обход дерева

Пошаговый перебор элементов дерева по связям между узлами-предками и узлами-потомками называется обходом дерева. Зачастую операция может быть выполнена переходом указателя по отдельным узлам. Обход, при котором каждый узел-предок просматривается прежде его потомков, называется предупорядоченным обходом или обходом в прямом порядке (pre-order walk), а когда просматриваются сначала потомки, а потом предки, то обход называется поступорядоченным обходом или обходом в обратном порядке (post-order walk). Существует также симметричный обход, при котором посещается сначала левое поддерево, затем узел, затем — правое поддерево, и обход в ширину, при котором узлы посещаются уровень за уровнем (N-й уровень дерева — множество узлов с высотой N). Каждый уровень обходится слева направо.

Общие операции

• вставка нового элемента в определённую позицию;
• вставка поддерева;
• добавление ветви дерева (называется прививкой);
• нахождение корневого элемента для любого узла;
• нахождение наименьшего общего предка двух вершин;
• перебор всех элементов дерева;
• перебор элементов ветви дерева;
• поиск изоморфного поддерева;
• поиск элемента;
• удаление ветви дерева (называется обрезкой);
• удаление поддерева;
• удаление элемента.

Общее применение

• управление иерархией данных;
• упрощение поиска информации (см. обход дерева);
• управление сортированными списками данных;
• синтаксический разбор арифметических выражений (англ. parsing), оптимизация программ;
• в качестве технологии компоновки цифровых картинок для получения различных визуальных эффектов;
• форма принятия многоэтапного решения (см. деловые шахматы).

См. также

• Двоичное разбиение пространства
• Куча (структура данных)
• Дерево (теория графов)
• Дерево (теория наборов)
• Древовидная структура
• Префиксное дерево
• Экспоненциальное дерево

Распространённые древовидные структуры

• Двоичное дерево

Самобалансирующиеся двоичные деревья поиска

• АА-дерево
• АВЛ-дерево
• Красно-чёрное дерево
• Расширяющееся дерево
• Дерево со штрафами

Прочие деревья

• B-дерево (2-3-дерево, B+-деревья, B*-дерево, UB-дерево)
• DSW-алгоритм
• Танцующее дерево
• Анфилада
• Смешанное дерево
• k-мерное дерево
• Октодерево
• Квадродерево
• R-дерево (структура_данных)
• Дерево покрытий
• Дерево остатков
• Сегментное дерево
• Список с пропусками
• T-дерево
• T-пирамида
• Верхнее дерево
• Дерево ван Емде Боаса
• Список структур данных (деревья)

Примечания

Литература

• Дональд Э. Кнут . Глава 2.3. Деревья // Искусство программирования = The Art of Computer Programming. — 3-е изд. — М.: Вильямс, 2000. — Т. 2. Основные алгоритмы. — 832 с. — 7000 экз. — ISBN 5-8459-0081-6 (рус.) ISBN 0-201-89684-2 (англ.).
• Томас Кормен , Чарльз Лейзерсон , Рональд Ривест , Клиффорд Штайн . Introduction to Algorithms. — 2nd Edition. — MIT Press, McGraw-Hill, 2001. — ISBN 0-262-03293-7.
• Section 10.4: Representing rooted trees, pp.214-217.
• Chapters 12-14 (Binary Search Trees, Red-Black Trees, Augmenting Data Structures), pp. 253—320.

Ссылки

• Описание из Словаря алгоритмов и структур данных
• Описание древовидных структур
• Обходы бинарных деревьев
• Красно-черные деревья

АВЛ-дерево

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 декабря 2015; проверки требуют 11 правок.

Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей.

 

АВЛ-дерево

Тип

дерево поиска

Изобретено в

1962 году

Изобретено

Адельсон-Вельский Георгий Максимович и Ландис Евгений Михайлович

Временная сложность
в О-символике

  В среднем В худшем случае Расход памяти O(n) O(n) Поиск O(log n) O(log n) Вставка O(log n) O(log n) Удаление O(log n) O(log n)

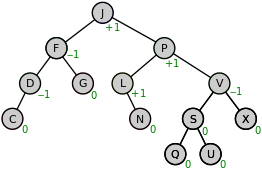
АВЛ-дерево — сбалансированное по высоте двоичное дерево поиска: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.

АВЛ — аббревиатура, образованная первыми буквами фамилий создателей (советских учёных) Адельсон-Вельского Георгия Максимовича и Ландиса Евгения Михайловича.

Содержание

• 1 Максимальная высота
• 2 Балансировка
• 3 Алгоритм добавления вершины
• 4 Алгоритм удаления вершины
• 5 Нерекурсивная вставка в АВЛ-дерево сверху-вниз
• 6 Нерекурсивное удаление из АВЛ-дерева сверху вниз
• 7 Расстановка балансов при удалении
• 8 Расстановка балансов при одинарном повороте
• 9 Расстановка балансов при двойном повороте
• 10 Оценка эффективности
• 11 См. также
• 12 Примечания
• 13 Литература

Максимальная высота

Максимальная высота АВЛ-дерева при заданном числе узлов ^[1]:

h ≤ ⌊ 1.45 log 2 ⁡ ( n + 2 ) ⌋ {\displaystyle h\;\leq \;\lfloor 1.45\log _{2}(n+2)\rfloor \;}

Количество возможных высот на практике сильно ограничено (при 32-битной адресации максимальная высота равна 45, при 48-битной — 68), поэтому лучше заранее подсчитать все возможные значения минимального количества узлов для каждой высоты с помощью рекуррентной формулы для дерева Фибоначчи:

n 0 = 0 {\displaystyle n_{0}=0} ,

n 1 = 1 {\displaystyle n_{1}=1} ,

n h = n h − 2 + n h − 1 + 1 {\displaystyle n_{h}=n_{h-2}+n_{h-1}+1} .

Промежуточные значения количества узлов будут соответствовать предыдущей (меньшей) высоте.

Балансировка

Относительно АВЛ-дерева балансировкой вершины называется операция, которая в случае разницы высот левого и правого поддеревьев = 2, изменяет связи предок-потомок в поддереве данной вершины так, что разница становится <= 1, иначе ничего не меняет. Указанный результат получается вращениями поддерева данной вершины.

Используются 4 типа вращений:

Малое левое вращение		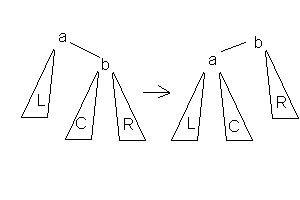Данное вращение используется тогда, когда высота b-поддерева — высота L = 2 и высота С <= высота R.
Большое левое вращение		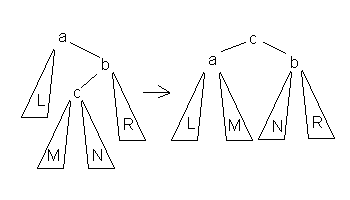Данное вращение используется тогда, когда высота b-поддерева — высота L = 2 и высота c-поддерева > высота R.
Малое правое вращение		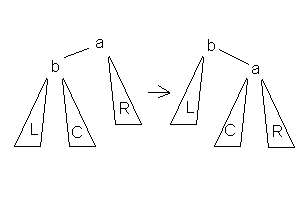Данное вращение используется тогда, когда высота b-поддерева — высота R = 2 и высота С <= высота L.
Большое правое вращение		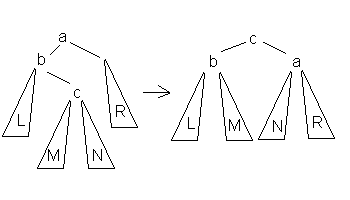Данное вращение используется тогда, когда высота b-поддерева — высота R = 2 и высота c-поддерева > высота L.

В каждом случае достаточно просто доказать то, что операция приводит к нужному результату и что полная высота уменьшается не более чем на 1 и не может увеличиться. Также можно заметить, что большое левое вращение это композиция правого малого вращения и левого малого вращения. Из-за условия балансированности высота дерева О(log(N)), где N- количество вершин, поэтому добавление элемента требует O(log(N)) операций.

Алгоритм добавления вершины

Показатель сбалансированности в дальнейшем будем интерпретировать как разность между высотой левого и правого поддерева, а алгоритм будет основываться на типе TAVLTree, описанном выше. Непосредственно при вставке (листу) присваивается нулевой баланс. Процесс включения вершины состоит из трех частей (данный процесс описан Никлаусом Виртом в «Алгоритмы и структуры данных»):

1. Прохода по пути поиска, пока не убедимся, что ключа в дереве нет.
2. Включения новой вершины в дерево и определения результирующих показателей балансировки.
3. «Отступления» назад по пути поиска и проверки в каждой вершине показателя сбалансированности. Если необходимо — балансировка.

Будем возвращать в качестве результата функции, уменьшилась высота дерева или нет. Предположим, что процесс из левой ветви возвращается к родителю (рекурсия идет назад), тогда возможны три случая: { h_l — высота левого поддерева, h_r — высота правого поддерева } Включение вершины в левое поддерево приведет к

1. h_l < h_r: выравняется h_l = h_r. Ничего делать не нужно.
2. h_l = h_r: теперь левое поддерево будет больше на единицу, но балансировка пока не требуется.
3. h_l > h_r: теперь h_l — h_r = 2, — требуется балансировка.

В третьей ситуации требуется определить балансировку левого поддерева. Если левое поддерево этой вершины (Tree^.left^.left) выше правого (Tree^.left^.right), то требуется большое правое вращение, иначе хватит малого правого. Аналогичные (симметричные) рассуждения можно привести и для включение в правое поддерево.

Алгоритм удаления вершины

Для простоты опишем рекурсивный алгоритм удаления. Если вершина — лист, то удалим её и вызовем балансировку всех её предков в порядке от родителя к корню. Иначе найдём самую близкую по значению вершину в поддереве наибольшей высоты (правом или левом) и переместим её на место удаляемой вершины, при этом вызвав процедуру её удаления.

Докажем, что данный алгоритм сохраняет балансировку. Для этого докажем по индукции по высоте дерева, что после удаления некоторой вершины из дерева и последующей балансировки высота дерева уменьшается не более, чем на 1. База индукции: Для листа очевидно верно. Шаг индукции: Либо условие балансированности в корне (после удаления корень может изменится) не нарушилось, тогда высота данного дерева не изменилась, либо уменьшилось строго меньшее из поддеревьев => высота до балансировки не изменилась => после уменьшится не более чем на 1.

Очевидно, что в результате указанных действий процедура удаления вызывается не более 3 раз, так как у вершины, удаляемой по второму вызову, нет одного из поддеревьев. Но поиск ближайшего каждый раз требует O(N) операций. Становится очевидной возможность оптимизации: поиск ближайшей вершины может быть выполнен по краю поддерева, что сокращает сложность до O(log(N)).