Общее уравнение плоскости: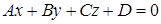 
,
где A, B, C – координаты вектора нормали вектора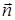 
(любого вектора, перпендикулярного данной плоскости), D – свободный член уравнения.
Уравнение плоскости, проходящей через точку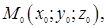 
перпендикулярно вектору 
:
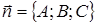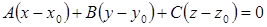. (48)
Уравнение плоскости, проходящей через три заданные точки
:
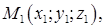
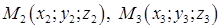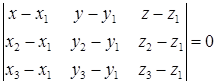. (49)
Угол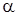 
между двумя плоскостями, заданными уравнениями 
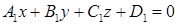и 
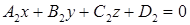определяется как угол между векторами их нормале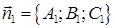й 
и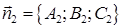 
или дополнительный к нему (обычно берется острый угол), то есть
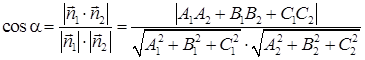. (50)
Уравнения прямой в пространстве
Параметрические уравнения прямой l в пространстве:
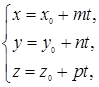(51)
где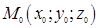 
– фиксированная точка прямой; 
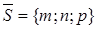– направляющий вектор прямой l, т. е. любой вектор, параллельный l; t – числовой параметр.
Каждому значению параметра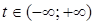 
соответствует единственная точка прямой l.
Канонические уравнения прямой:
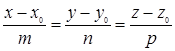. (52)
Уравнения прямой, проходящей через две данные точки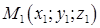 
и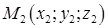 
:
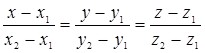. (53)
Углом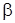 
между прямыми называют угол между их направляющими векторами 
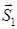= {m1; n1; p1} и 
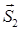= {m2; n2; p2}, или дополнительный к нему (обычно берется острый угол), т. е.
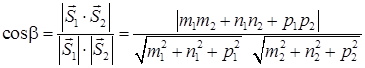. (54)
Углом между плоскостью и прямой l (в случае их пересечения) называется угол между прямой и её проекцией на плоскость. Синус угла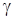 
между плоскостью 
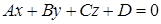и прямой 
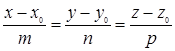определяется по формуле:
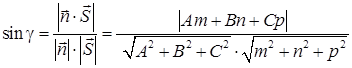. (55)
Примерный вариант и образец выполнения
контрольной работы № 2
Задача 1. Даны многочлен f(x) и матрица А:
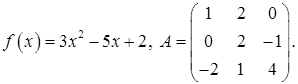
Требуется найти значение матричного многочлена f (A).
Задача 2. Дана система трех линейных алгебраических уравнений
с тремя неизвестными: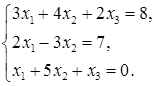 
Требуется:
1) записать систему в матричном виде;
2) найти решение системы с помощью формул Крамера;
3) решить систему при помощи обратной матрицы.
Задача 3. Даны координаты трех векторов: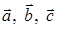 
и вектор 
:
, 
.
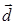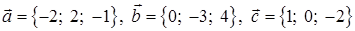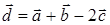Требуется:
1) вычислить модуль вектора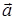 
;
2) найти координаты вектора ;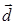
3) найти угол φ между векторами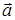 
и 
;
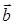4) вычислить проекцию вектора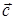 
на направление вектора 
;
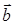5) вычислить площадь треугольника, построенного на векторах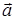 
и ;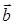
6) вычислить объем параллелепипеда, построенного на векторах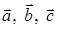 
.
Задача 4. Даны координаты точек – вершин пирамиды ABCD:
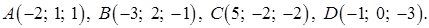
Требуется:
1) вычислить длину ребра AB;
2) найти уравнение плоскости грани ABC;
3) найти угол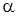 
между гранями ABC и BCD;
4) составить параметрические уравнения прямой AB;
5) составить канонические уравнения высоты пирамиды DK, проведенной из вершины D;
6) найти координаты точки пересечения DK и грани ABC;
7) найти угол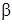 
между ребрами AB и BC;
8) найти угол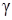 
между ребром AD и гранью ABC;
9) сделать чертеж пирамиды в системе координат.
Решение задачи 1
Записываем матричный многочлен: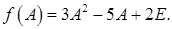 
Здесь Е – единичная матрица той же размерности, что и А, т. е. 3-го порядка.
Найдем матрицу A2. При умножении матрицы A на себя используем правило "строка на столбец" (формула (23)):
A2 = A·A =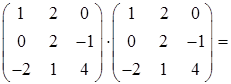 
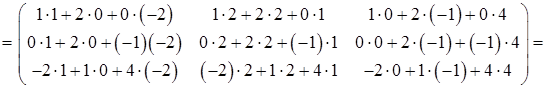
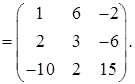
Найдем матрицу 2Е, используя правило умножения матрицы на число (формула (21)):
E =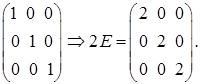 
Теперь найдем значение матричного многочлена f(A), используя правило умножения матрицы на число и правило сложения матриц (формула (22)):
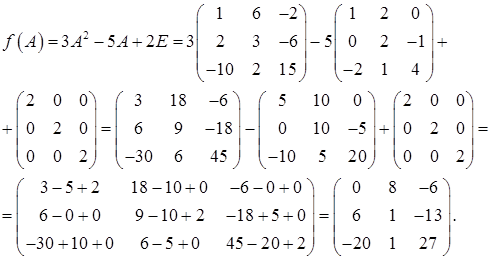
Ответ: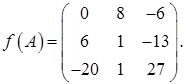 
Решение задачи 2
1) Запишем систему в матричном виде:
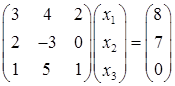, или AX = B,
где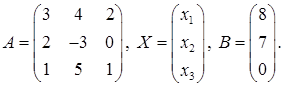 
(Во втором уравнении системы отсутствует неизвестная х3, т. е. а23 = 0).
2) Решим систему с помощью формул Крамера. Для этого по формулам (29) составляем главный определитель системы из коэффициентов при неизвестных в левых частях уравнений и три вспомогательных определителя:
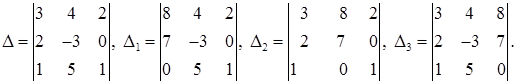
Вычислим эти определители, используя формулу (25):
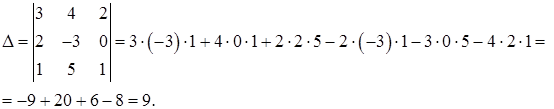
Так как ∆ ≠ 0, то данная система имеет единственное решение.
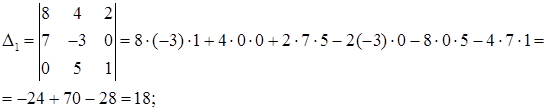
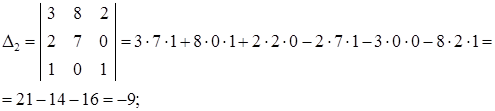
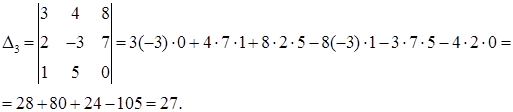
Найдем решение системы по формулам Крамера (30):
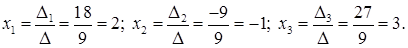
3) Решим систему при помощи обратной матрицы.
a) Определитель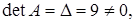 
следовательно, обратная матрица существует.
б) Чтобы найти союзную матрицу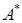 
к матрице А, необходимо вычислить по формулам (26) алгебраические дополнения всех ее элементов:
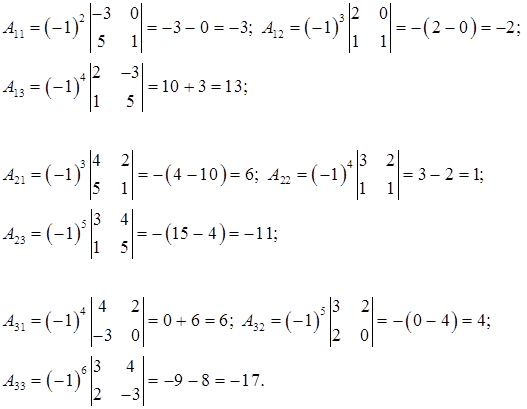
Здесь определители 2-го порядка вычислены по формуле (24).
Тогда союзная матрица (см. формулу (31)):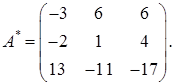 
в) Найдем обратную матрицу по формуле (32):
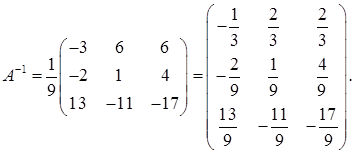
г) Получим решение системы при помощи обратной матрицы по формуле (33) (правило "строка на столбец"):
.
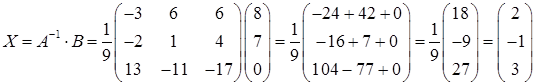
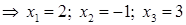Решение, полученное матричным способом, совпадает с тем, которое получено по формулам Крамера, что подтверждает правильность этого решения.
Ответы:
1) система в матричном виде: AX = B, где
;
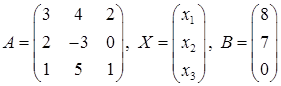2) решение системы, полученное с помощью формул Крамера:
;
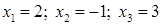3) решение системы, полученное при помощи обратной матрицы:
.
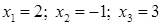Решение задачи 3
1) Модуль вектора 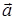вычисляется по формуле (35):
.
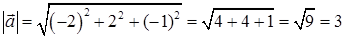2) Чтобы найти координаты вектора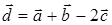 
, используем формулы (38) и (39):
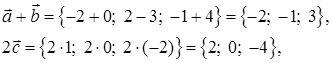
тогда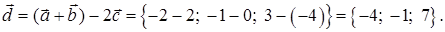 
3) Косинус угла между векторам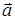и 
и 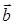найдем по формуле (41):
.
Для этого вычислим скалярное произведение 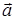и 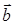по формуле (40): 
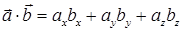= –2∙0 + 2∙(–3) + (–1)∙4 = –10, затем модуль вектора :
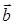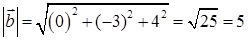, тогда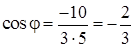 
и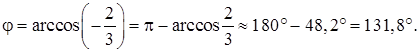 
4) Проекцию вектора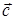 
на направление 
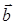вычислим по формуле (42):
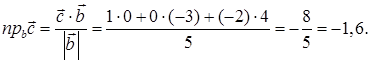
5) Площадь треугольника, построенного на векторах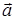 
и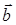 
найдем по формуле (44). Для этого сначала находим векторное произведение этих векторов по формуле (43):
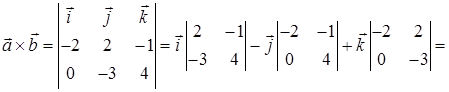
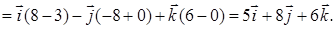
Следовательно, площадь треугольника, построенного на векторах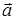 
и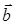 
:
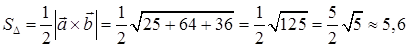(кв. ед.).
6) Для вычисления объема параллелепипеда, построенного на векторах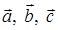 
находим смешанное произведение векторов по формуле (45):
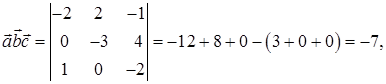
тогда объема параллелепипеда по формуле (47):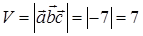 
.
Ответы:
1) модуль вектора :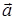 
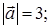
2) координаты вектора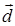 
: 
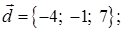
3) угол между векторам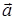и 
и :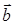 
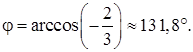
4) проекция вектора 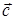на направление вектора : 
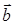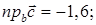
5) площадь треугольника, построенного на векторах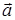 
и :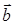 
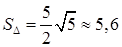(кв. ед.);
6) объем параллелепипеда, построенного на векторах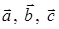 
:
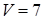(куб. ед.).
Решение задачи 4
1) Длину ребра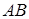 
найдем по формуле (36):
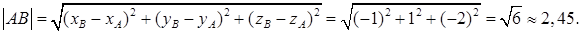
2) Чтобы получить уравнение плоскости грани ABC, необходимо найти вектор, перпендикулярный плоскости ABC, т. е. вектор, перпендикулярный векторам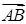 
и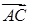 
. Одним из таких векторов является векторное произведение 
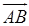на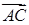 
. Для того, чтобы найти его, сначала вычислим координаты векторов по формуле (37):
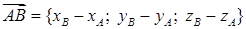= {–3–(–2); 2–1; –1–1} = {–1; 1; –2},
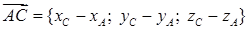= {7; –3; –3}.
Векторное произведение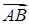 
и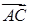 
найдем по формуле (43):
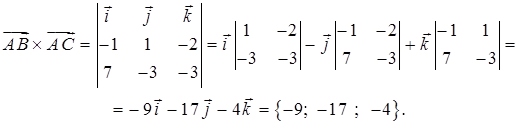
В качестве вектора нормали к плоскости ABC можно взять любой вектор, коллинеарный полученному, например,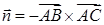 
= {9; 17; 4}. Используем уравнение плоскости, проходящей через точку 
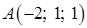перпендикулярно вектору 
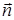(формула (48):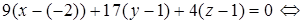 
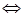
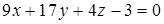– уравнение плоскости грани ABC .
3) Прежде, чем найти угол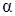 
между гранями ABC и BCD, получим уравнение грани BCD, используя уравнение плоскости, проходящей через три заданные точки 
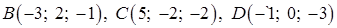(формула (49):
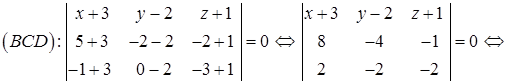
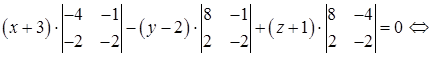
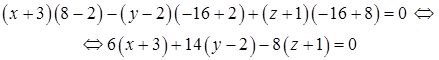
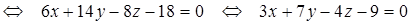– уравнение грани BCD.
Из уравнения плоскости BCD возьмем координаты вектора нормали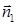 
, перпендикулярного этой плоскости: 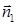={3; 7; –4}.
Косинус угла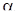 
между плоскостями (гранями) ABC и BCD найдем
по формуле(50):
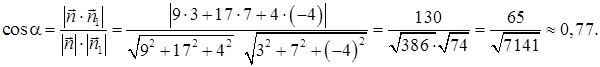
Отсюда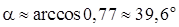 
.
4) Уравнения ребра AB можно записать как параметрические уравнения прямой, проходящей через точку A(–2; 1; 1) и имеющей направляющий вектор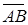 
= {–1; 1; –2} (формулы (51)):
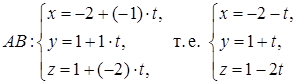– параметрические уравнения AB.
Другой способ: можно использовать уравнения прямой, проходящей через две точки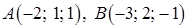 
(формулы (53)):
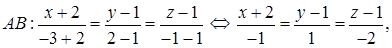
откуда, обозначив каждую из дробей t, получаем:
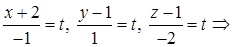
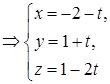– параметрические уравнения AB.
5) Высота пирамиды DK – это прямая, проведенная из вершины D перпендикулярно грани ABC. Она имеет направляющий вектор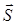 
, коллинеарный вектору нормали плоскости ABC. Можно взять, например, 
= 
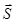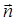= {9; 17; 4}. Запишем канонические уравнения высоты DK, используя точку D(–1; 0; –3)
и вектор 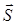= {9; 17; 4} (формулы (52)):
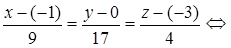
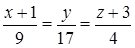– канонические уравнения DK.
6) Прежде, чем найти точку пересечения DK и грани ABC, получим параметрические уравнения прямой DK. Обозначив каждую из дробей
в канонических уравнениях буквой t, получаем:
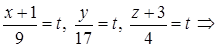
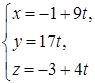– параметрические уравнения DK.
Точка пересечения DK и грани ABC (точка К) лежит на прямой, а значит, имеет координаты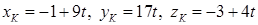 
, и принадлежит плоскости, т. е. ее координаты удовлетворяют уравнению плоскости ABC. Поэтому координаты точки K найдем, решив систему:
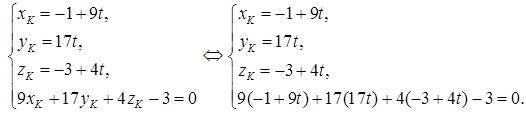
Решим последнее уравнение относительно t:
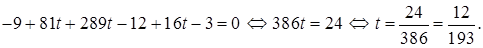
Вычислим координаты точки K, подставив найденное значение параметра в первые три уравнения системы:
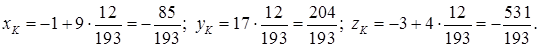
Итак, точка пересечения DK и грани ABC: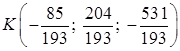 
.
7) Угол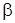 
между ребрами AB и BC найдем, как угол между на-
правляющими векторами прямых AB и BC: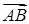 
= {–1; 1; –2}
и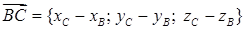 
= {8; –4; –1}. Найдем косинус угла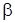 
по формуле(54):
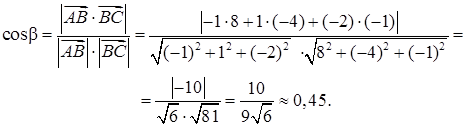
Тогда угол между ребрами AB и BC: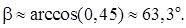 
8) Чтобы определить угол 
между ребром AD и гранью ABC, найдем направляющий вектор прямой: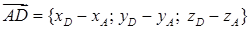 
= {1; –1; –4}. Плоскость ABC имеет вектор нормали 
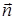= {9; 17; 4}. Синус угла 
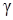между прямой 
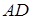и плоскостью ABC можно вычислить по формуле (55):
 |
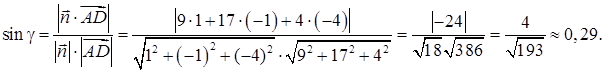
Тогда угол между ребром AD и гранью ABC:
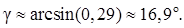
9) Выполним чертеж пирамиды в системе координат (рис. 19).
Ответы:
1) 
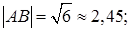
2) АВС: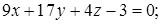 
3) 
;
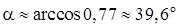4) 
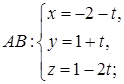
5) DK: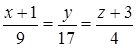 
;
6) 
;
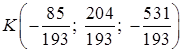7) 
;
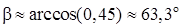8) 
;
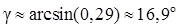9) чертеж пирамиды на рис. 19.
Варианты контрольнЫХ работ
Каждый вариант контрольной работы № 1 для студентов-заочников
1 курса всех специальностей содержит 5 задач, охватывающих материал по теме "Аналитическая геометрия на плоскости". Каждый вариант контрольной работы № 2 содержит 4 задачи по темам "Элементы линейной алгебры. Аналитическая геометрия в пространстве".
Перед выполнением каждой контрольной работы студенту необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии с методическими указаниями, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы.
Задания для всех вариантов общие; студенту следует выбрать из условия каждой задачи данные, необходимые для ее решения, в соответствии со своим вариантом. Оформление контрольных работ должно соответствовать установленным правилам и требованиям. Необходимые чертежи должны выполняться четко, с соответствующими подписями и комментариями (см. образец выполнения примерного варианта работы).
Варианты контрольной работы № 1
Задача 1. Даны координаты вершин треугольника АВС.
| Номер варианта | Координаты точек | Номер варианта | Координаты точек |
| 1 | А(–2; –3), В(2; 7), С(6; –1) | 6 | А(3; –3), В(–4; 1), С(–2; 5) |
| 2 | А(–5; 1), В(6; 3), С(–4; –7) | 7 | А(3; 5), В(–2; 2), С(2; –4) |
| 3 | А(4; 5), В(–3; 2), С(5; –4) | 8 | А(–2; 4), В(5; 6), С(3; –4) |
| 4 | А(7; –7), В(1; 2), С(–5; –4) | 9 | А(3; 7), В(–4; 1), С(–2; –5) |
| 5 | А(–3; 4), В(4; 5), С(8; –3) | 10 | А(4; 3), В(–3; –2), С(–7; 2) |
Требуется:
1) вычислить длину стороны ВС;
2) составить уравнение стороны ВС;
3) найти внутренний угол треугольника при вершине В;
4) составить уравнение высоты АК, проведенной из вершины А;
5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан);
6) сделать чертеж в системе координат.
Задача 2. Даны координаты точки А, уравнение прямой l и число λ.
| Номер варианта | Координаты точки | Уравнение прямой l | Число λ | Номер варианта | Координаты точки | Уравнение прямой l | Число λ |
| 1 | А(–1; 0) | y + 2 = 0 | 1 : 1 | 6 | А(–5; 1) | x + 1 = 0 | 1: 1 |
| 2 | А(3; 1) | 3x = 16 | 3 : 4 | 7 | А(5; –4) | 5x = 1 | 5 : 1 |
| 3 | А(3; 0) | x = 0 | 2 : 1 | 8 | А(1; 0) | 2x = 7 | 2 : 3 |
| 4 | А(2; 0) | 4x = 1 | 4 : 3 | 9 | А(1; 2) | x = 4 | 1 : 2 |
| 5 | А(0; 0) | 2x + 5 = 0 | 2 : 3 | 10 | А(3; 2) | 3x = 1 | 3 : 1 |
Найти уравнение траектории точки М, которая движется в плоскости так, что отношение ее расстояний до точки А и до прямой l равно λ. Сделать чертеж в системе координат.
Задача 3. Дано уравнение кривой 2-го порядка.
| Номер варианта | Уравнение кривой | Номер варианта | Уравнение кривой |
| 1 | 7x2 – 9y2 + 42x+ 18y – 9 = 0 | 6 | 9x2 + 4y2 – 54x + 8y + 49 = 0 |
| 2 | x2 + 2x – 12y + 37 = 0 | 7 | x2 – 10x + 4y + 17 = 0 |
| 3 | 5x2 + 9y2 + 10x – 54y + 41 = 0 | 8 | 3x2 – y2 – 30x – 2y + 62 = 0 |
| 4 | y2 + 6x + 6y – 3 = 0 | 9 | y2 – 8x – 4y – 4 = 0 |
| 5 | 5x2 – 4y2 – 20x – 24y – 36 = 0 | 10 | 7x2 + 16y2 – 56x + 64y + 64 = 0 |
Привести заданное уравнение к каноническому виду путем параллельного переноса осей координат. Определить тип кривой, найти ее характерные элементы в исходной системе координат. Изобразить на чертеже расположение кривой относительно обеих систем координат.
Задача 4. Даны уравнение кривой 2-го порядка и уравнение прямой.
| Номер варианта | Уравнение кривой | Уравнение прямой |
| 1 | x2 + 2y2 – 2x + 8y + 3 = 0 | x + 2y + 3 = 0 |
| 2 | x2 – 2y2 + 4x + 4y – 6 = 0 | x + 2y = 0 |
| 3 | x2 + 6x – 16y + 25 = 0 | x – 4y + 15 = 0 |
| 4 | x2 + 4y2 – 6x + 8y + 5 = 0 | x – 2y – 5 = 0 |
| 5 | y2 – 4x – 6y – 15 = 0 | 2x + y – 3 = 0 |
| 6 | x2 – 5y2 + 10x + 20y – 15 = 0 | x – 5y + 15 = 0 |
| 7 | x2 + 4y2 + 2x – 32y + 45 = 0 | x – y + 5 = 0 |
| 8 | x2 – 4x + 8y + 44 = 0 | x – 2y – 20 = 0 |
| 9 | 2x2 – y2 – 16x – 6y + 19 = 0 | x – y – 7 = 0 |
| 10 | y2 + 10x + 8y – 34 = 0 | 2x + y + 4 = 0 |
Требуется:
1) привести заданное уравнение кривой 2-го порядка к каноническому виду;
2) найти точки пересечения кривой и заданной прямой;
3) построить обе линии в исходной системе координат.
Задача 5. Дано уравнение кривой в полярной системе координат (ПСК).
| Номер варианта | Уравнение кривой | Номер варианта | Уравнение кривой |
| 1 |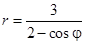 
| 6 |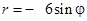 
|
| 2 |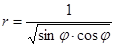 
| 7 |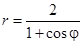 
|
| 3 |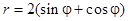 
| 8 |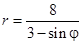 
|
| 4 |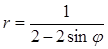 
| 9 |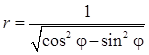 
|
| 5 |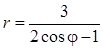 
| 10 |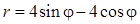 
|
Требуется:
1) найти область определения функции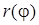 
;
2) построить кривую в ПСК, вычислив значения функции в точках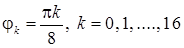 
, принадлежащих области определения функции 
;
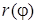3) найти уравнение заданной кривой в декартовой системе координат (ДСК), начало координат в которой совпадает с полюсом ПСК, а положительная полуось ОХ – с полярной осью ОР;
4) определить тип кривой.
Варианты контрольной работы № 2
Задача 1. Даны многочлен f(x) и матрица А.
| Номер варианта | Многочлен f ( x ) | Матрица А |
| 1 |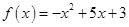 
| 
|
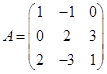
| 2 |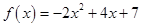 
| 
|
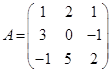
Окончание таблицы
| Номер варианта | Многочлен f ( x ) | Матрица А |
| 3 |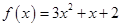 
| 
|
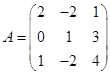
| 4 |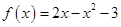 
| 
|
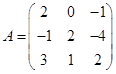
| 5 |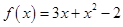 
| 
|
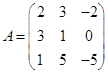
| 6 |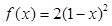 
| 
|
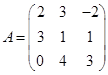
| 7 |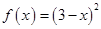 
| 
|
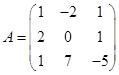
| 8 |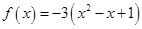 
| 
|
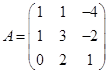
| 9 |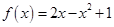 
| 
|
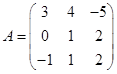
| 10 |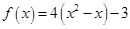 
| 
|
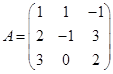
Требуется найти значение матричного многочлена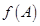 
.
Задача 2. Дана система трех линейных алгебраических уравнений
с тремя неизвестными.
| Номер варианта | Система уравнений | Номер варианта | Система уравнений |
| 1 |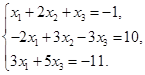 
| 6 |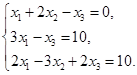 
|
| 2 |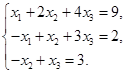 
| 7 |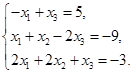 
|
| 3 |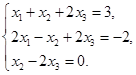 
| 8 |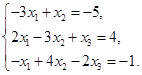 
|
| 4 |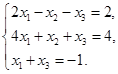 
| 9 |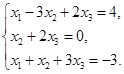 
|
| 5 |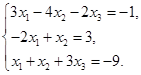 
| 10 |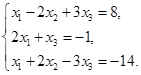 
|
Требуется:
1) записать систему в матричном виде;
2) найти решение системы с помощью формул Крамера;
3) решить систему при помощи обратной матрицы.
Задача 3. Даны координаты трех векторов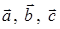 
и вектор 
.
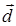| Номер варианта | Векторы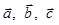 
| Вектор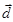 
|
| 1 |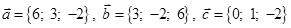 
| 
|
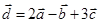
| 2 |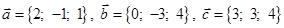 
| 
|
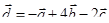
| 3 |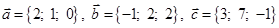 
| 
|
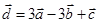
Окончание таблицы
| Номер варианта | Векторы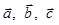
| Вектор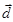
|
| 4 |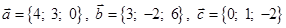 
| 
|
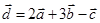
| 5 |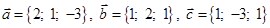 
| 
|
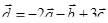
| 6 |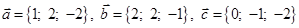 
| 
|
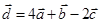
| 7 |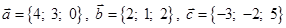 
| 
|
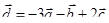
| 8 |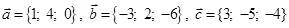 
| 
|
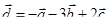
| 9 |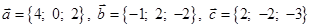 
| 
|
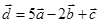
| 10 |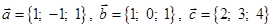 
| 
|
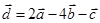
Требуется:
1) вычислить модуль вектора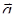 
;
2) найти координаты вектора ;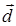
3) найти угол φ между векторами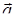 
и 
;
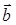4) вычислить проекцию вектора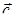 
на направление вектора ;
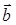5) вычислить площадь треугольника, построенного на векторах 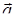и ;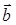
6) вычислить объем параллелепипеда, построенного на векторах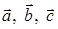 
.
Задача 4. Даны координаты точек – вершин пирамиды ABCD.
| Номер варианта | Координаты точек |
| 1 | А(1; 2; –1), В(0; 0; 1), С(1; –3; 3), D(2; –1; –1) |
| 2 | А(7; 2; 4), В(7; –1; –2), С(3; 3; 1), D(4; 2; 1) |
| 3 | А(1; 3; 6), В(2; 2; 1), С(–1; 0; 1), D(–4; 6; –3) |
| 4 | А(–2; 0; –4), В(–1; 7; 1), С(4; –8; –4), D(1; –4; 6) |
| 5 | А(1; 2; 0), В(3; 0; –1), С(5; –2; 3), D(3; 2; –1) |
| 6 | А(–1; 1; 2), В(2; 1; –2), С(–2; 0; 4), D(2; –1; 2) |
| 7 | А(4; 2; 5), В(2; –3; 0), С(–10; 5; 8), D(–5; 2; 4) |
| 8 | А(2; –1; 1), В(–1; –3; 2), С(–2; 3; 1), D(–1; 2; –3) |
| 9 | А(–1; 1; 2), В(–2; 0; 3), С(3; 6; –3), D(–1; –2; 7) |
| 10 | А(4; –1; 3), В(–2; 1; 0), С(0; –5; 1), D(–2; 1; –1) |
Требуется:
1) вычислить длину ребра AB;
2) найти уравнение плоскости грани ABC;
3) найти угол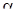 
между гранями ABC и BCD;
4) составить параметрические уравнения прямой AB;
5) составить канонические уравнения высоты пирамиды DK, проведенной из вершины D;
6) найти координаты точки пересечения DK и грани ABC;
7) найти угол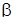 
между ребрами AB и BC;
8) найти угол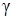 
между ребром AD и гранью ABC;
9) сделать чертеж пирамиды в системе координат.
Рекомендуемая литература
1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. – М. : Айрис-пресс, 2003. – 288 с.
2. Щипачев, В.С. Высшая математика : учебник для вузов / В.С. Щипачев.– М. : Высш. шк., 1998. – 479 с.
3. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 1
/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М. : Высш. шк., 1999. – 304 с.
4. Щипачев, В.С. Задачник по высшей математике / В.С. Щипачев. – М. : Высш. шк., 2001. – 304 с.
Налоговая льгота – Общероссийский классификатор продукции
ОК 005-93, т. 2; 95 3004 – воспитательная, образовательная и педагогическая литература
Издательство МГТУ. 183010 Мурманск, Спортивная, 13.
Сдано в набор 14.09.2007. Подписано в печать 18.09.2007. Формат 60´841/16.
Бум. типографская. Усл. печ. л. 2,79. Уч.-изд. л. 2,18. Заказ 443. Тираж 300 экз.
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ
Федеральное государственное образовательное учреждение высшего профессионального образования
"Мурманский государственный технический университет"
Аналитическая геометрия
на плоскости.
Элементы линейной алгебры.
Аналитическая геометрия
в пространстве
Часть 1
Мурманск
2007
Дата: 2018-12-28, просмотров: 214.
