МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ
Федеральное государственное образовательное учреждение высшего профессионального образования
"Мурманский государственный технический университет"
Кафедра высшей математики
и программного обеспечения ЭВМ
Аналитическая геометрия на плоскости.
Элементы линейной алгебры.
Аналитическая геометрия в пространстве
Часть 1
Методические рекомендации к выполнению контрольных
работ по дисциплине "Математика"
для студентов I курса вечерне-заочного факультета
Мурманск
2007
УДК 514.2 + 512.64 + 514.144.2 (075.8)
ББК 22.151.5 + 22.143 Я73
М 33
Составители: Л.Г. Мостовская, доцент кафедры высшей математики
и программного обеспечения ЭВМ Мурманского государственного технического университета;
Е.Е. Великая, ст. преподаватель той же кафедры
Методические рекомендации рассмотрены и одобрены кафедрой
15 февраля 2006 г., протокол № 4
Рецензент - В.С. Кацуба, канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ
Оригинал-макет подготовлен в авторской редакции
Электронная верстка Т.В. Бекреневой
Ó Мурманский государственный
технический университет, 2007
Оглавление
Введение.. 4
Методические указания к изучению тем "Аналитическая геометрия на плоскости" И "Элементы линейной алгебры. Аналитическая геометрия в пространстве". 5
Справочный материал по теме
"Аналитическая геометрия на плоскости". 6
1. Декартова система координат (ДСК) на плоскости. 6
2. Полярная система координат (ПСК) 7
3. Прямая линия на плоскости. 7
4. Кривые второго порядка. 8
Примерный вариант и образец выполнения
контрольной работы № 1. 11
Справочный материал по темам
"Элементы линейной алгебры.
Аналитическая геометрия в пространстве". 19
1. Матрицы.. 19
2. Линейные операции над матрицами. 20
3. Определители. 21
4. Решение системы трех линейных алгебраических уравнений
с тремя неизвестными методом Крамера. 22
5. Решение системы трех линейных алгебраических уравнений
при помощи обратной матрицы.. 23
6. Векторы. Операции над векторами. 24
7. Уравнение плоскости в пространстве. 27
8. Уравнения прямой в пространстве. 27
Примерный вариант и образец выполнения
контрольной работы № 2. 28
Варианты контрольнЫХ работ. 39
Варианты контрольной работы № 1. 39
Варианты контрольной работы № 2. 41
Рекомендуемая литература.. 45
Введение
Основной формой обучения студентов-заочников математике является самостоятельная работа студентов, которая включает изучение теоретического материала, решение типовых задач с проверкой правильности решения, выполнение контрольных работ.
В настоящих рекомендациях содержатся краткие теоретические сведения, рекомендации к выполнению контрольной работы 1 по теме "Аналитическая геометрия на плоскости" и контрольной работы 2 по теме "Элементы линейной алгебры. Аналитическая геометрия в пространстве", список литературы.
В результате изучения указанных тем студенты I курса должны:
• освоить метод координат на плоскости и научиться решать простые геометрические задачи с использованием уравнений прямой и уравнений кривых второго порядка;
• ознакомиться с основами линейной алгебры (действия над матрицами, вычисление определителей), научиться решать системы линейных алгебраических уравнений методом Крамера и с помощью обратной матрицы;
• знать основы векторной алгебры (линейные операции над векторами, скалярное, векторное и смешанное произведения векторов и их приложения);
• освоить метод координат в пространстве, научиться решать задачи
с использованием средств аналитической геометрии.
В предлагаемых методических рекомендациях даны варианты контрольных работ, справочный материал, необходимый для их выполнения,
а также примеры решения контрольных работ.
Методические указания к изучению тем
"Аналитическая геометрия на плоскости"
И "Элементы линейной алгебры.
Аналитическая геометрия в пространстве"
В таблице приведены наименования тем в соответствии с содержанием контрольных работ и необходимая литература. Перед выполнением контрольных работ рекомендуется изучить соответствующий теоретический материал и решить указанные в таблице задачи.
Таблица 1
| Номер конт-рольной работы | Номер задачи | Наименования тем | Литература |
| 1 | 1 | Декартовы координаты точек на плоскости. Расстояние между двумя точками на плоскости. Деление отрезка в данном отношении. Уравнения прямой линии на плоскости. Условия параллельности и перпендикулярности прямых на плоскости | [1], гл. III, § 9.1, 9.2, 10.1, 10.2, 10.3; [2], гл. 3, § 1 - 2, 5, 6; [3], ч. 1, гл.I, № 16 - 20, 74, 76, 99, 100, 102, 105, 111 - 114, 119, 121; [4], гл. 3, № 21, 24, 25, 29, 39, 86 - 88, 91, 94, 95, 122 |
| 1 | 2 | Уравнения линий на плоскости в декартовых координатах | [1], гл. III, § 10.1; [2], гл. 3, § 5; [3], ч. 1, гл. I, № 44, 47, 48, 150; [4], гл. 3, № 52, 55, 60 - 67, 136, 148, 159 |
| 1 | 3, 4 | Кривые второго порядка: окружность, эллипс, гипербола, парабола. Приведение уравнения второго порядка к каноническому виду. Точки пересечения линий на плоскости | [1], гл. III, § 9.3, 11; [2], гл. 3, § 7, 8; [3], ч. 1, гл. I, № 134, 136, 144, 145, 149, 155 - 157, 169, 170, 187 - 195; [4], гл. 3, № 126, 128, 139, 141, 150 - 152, 156 |
| 1 | 5 | Полярные координаты точки на плоскости. Связь между декартовыми и полярными координатами. Уравнения линий на плоскости в полярных координатах | [1], гл. III, § 9.1, 10.1; [2], гл. 3, § 3, 5; [3], ч. 1, гл. I, № 29, 30, 33 - 35, 49 - 51; [4], гл. 3, № 44, 45, 53(5), 54 |
| 2 | 1 | Матрицы. Операции над матрицами | [1], гл. I, § 1; [2], гл. 10, § 1; [3], ч. 1, гл. IV, № 399 - 403, 414, 415 |
| 2 | 2 | Определители. Обратная матрица. Решение систем линейных алгебраических уравнений по формулам Крамера и с помощью обратной матрицы | [1], гл. I, § 2, 3.1, 3.2, 4.1, 4.3; [2], гл. 10, § 2 - 4; [3], ч. 1, гл. I, № 210, 211, 217, 219, 225 - 227; [4], гл. 7, № 20 - 25, 38 - 43 |
Окончание табл. 1
| Номер конт-рольной работы | Номер задачи | Наименования тем | Литература |
| 2 | 3 | Линейные операции над векторами. Скалярное, векторное, смешанное произведения векторов | [1], гл. II, § 5 - 8; [2], гл. 9, § 1 - 4, 6 - 8; [3], ч. 1, гл. II, № 244, 248, 256 - 266, 284; [4], гл. 10, № 37, 47, 48, 51, 72, 73, 77, 83 - 84 |
| 2 | 4 | Плоскость и прямая линия в пространстве | [1], гл. IV, § 12.1 - 12.6; [2], гл. 9, § 11 - 13; [3], ч. 1, гл. III, № 288, 289, 302, 307, 314, 325, 333, 334, 341; [4], гл. 10, № 104, 113, 119, 131, 132, 141, 151, 153 |
Примечание. Ссылки на литературу в таблице даны в соответствии
с номерами в списке рекомендуемой литературы.
Справочный материал по теме
"Аналитическая геометрия на плоскости"
Прямая линия на плоскости
 Общее уравнение прямой на плоскости:
Общее уравнение прямой на плоскости:
Ах + В у + С = 0.
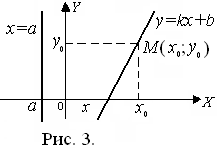
Уравнение прямой с угловым коэффициентом (рис. 3):
у = k x + b. (6)
Уравнение вертикальной прямой (рис. 3):
х = а. (7)
Уравнения прямых, проходящих через одну заданную точку М(х0; у0) (уравнение пучка прямых):
у – y0 = k(x – x0). (8)
Угловой коэффициент прямой, проходящей через две заданные точки А(х1; у1) и В(х2; у2):
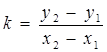 . (9)
. (9)
Уравнение прямой, проходящей через две заданные точки:
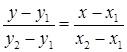 . (10)
. (10)
Пусть на плоскости заданы две прямые, которым соответствуют уравнения с угловыми коэффициентами: у = k1 x + b1 и у = k2 x + b2.
Условие параллельности прямых на плоскости:
k1 = k2. (11)
Условие перпендикулярности прямых:
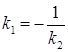 . (12)
. (12)
Если одна из двух перпендикулярных прямых вертикальная, т.е. k2 не существует, то k1 = 0 и обратно: если k2 = 0, то k1 не существует.
Тангенс острого угла между пересекающимися прямыми можно найти, используя формулу:
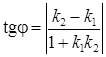 , (13)
, (13)
откуда 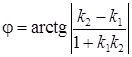 . Если одна из прямых вертикальная, т.е. k2 не существует, то
. Если одна из прямых вертикальная, т.е. k2 не существует, то 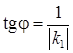 .
.
Кривые второго порядка
 Каноническое уравнение эллипса:
Каноническое уравнение эллипса:
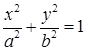 . (14)
. (14)
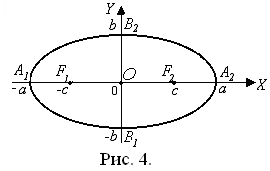
Термины и обозначения основных элементов эллипса (рис. 4):
O – центр эллипса;
с – фокусное расстояние;
F1(– c; О), F2(c; О) – фокусы эллипса;
|А1А2| = 2a – длина большой оси;
а – большая полуось эллипса;
| B1B2| = 2b – длина малой оси;
b – малая полуось эллипса.
Для эллипса справедливо: c2 = a2 – b2.
Число 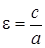 называется эксцентриситетом эллипса
называется эксцентриситетом эллипса 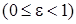 .
.
Если a < b, то эллипс имеет вытянутую по вертикали форму (рис. 5).
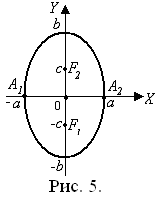 В этом случае фокусы эллипса F1(О; – c), F2(О; c), эксцентриситет
В этом случае фокусы эллипса F1(О; – c), F2(О; c), эксцентриситет  и справедливо c2 = b2 – a2.
и справедливо c2 = b2 – a2.
Если a = b, то уравнение эллипса становится уравнением окружности:
x2 + y2 = R2,
где R = a = b .
В этом случае фокусы эллипса совпадают с центром окружности, фокусное расстояние с = 0, эксцентриситет окружности 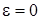 .
.
Каноническое уравнение гиперболы:
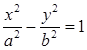 . (15)
. (15)
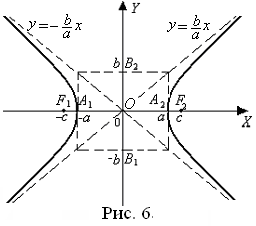 Термины и обозначения основных элементов гиперболы (рис. 6):
Термины и обозначения основных элементов гиперболы (рис. 6):
O – центр гиперболы;
с – фокусное расстояние;
F1(– c; 0), F2(c; 0) – фокусы гиперболы;
|А1А2| = 2a – длина вещественной оси;
а – вещественная полуось гиперболы;
| B1B2| = 2b – длина мнимой оси;
b – мнимая полуось гиперболы.
Уравнения асимптот гиперболы:
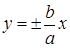 .
.
Для гиперболы справедливо: с2 = a2 + b2.
Число 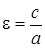 называется эксцентриситетом гиперболы
называется эксцентриситетом гиперболы 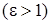 .
.
Канонические уравнения параболы.
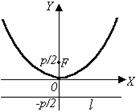 Рис. 7
Рис. 7
| Существуют 4 вида канонических уравнений параболы: х2 = 2ру. (16) Фокус F(0; х2 = –2ру. (17) Фокус F(0; – у2 = 2рх. (18) Фокус F( у2 = –2рх. (19) Фокус F(– |
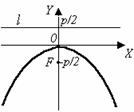 Рис. 8
Рис. 8
| |
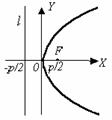 Рис. 9
Рис. 9
| |
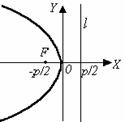 Рис. 10
Рис. 10
|
Термины и обозначения основных элементов параболы: O – вершина параболы, F – фокус параболы, p – параметр параболы (расстояние от фокуса F до директрисы l).
Для приведения уравнения кривой со смещенным центром к каноническому виду может быть использован параллельный перенос системы координат в точку O1(α; β).При параллельном переносе координаты любой точки М (х; у) в новой системе координат X1O1Y1 будут (х1; у1), где
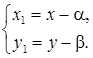 (20)
(20)
Примеры таких преобразований приведены в табл. 2.
Таблица 2
| В системе координат ХО Y | В системе координат X 1 O 1 Y 1 |
Окружность с центром в точке O1(α; β) и с радиусом R:
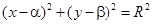
| Каноническое уравнение окружности:
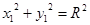
|
Эллипс с центром в точке O1(α; β):
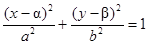
| Каноническое уравнение эллипса:
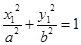
|
Гипербола с центром в точке O1(α; β): 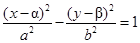
| Каноническое уравнение гиперболы: 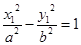 . .
|
Параболы с вершиной в точке O1(α;β) 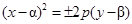 или
или 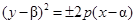 . .
| Канонические уравнения парабол:
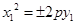 или или 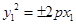
|
Примерный вариант и образец выполнения
контрольной работы № 1
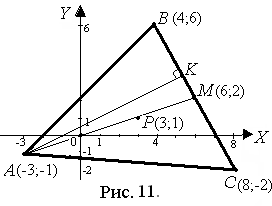
Задача 1. Даны координаты вершин треугольника АВС: А(–3; –1),
В(4; 6), С(8; –2).
Требуется:
1) вычислить длину стороны ВС;
2) составить уравнение стороны ВС;
3) найти внутренний угол треугольника при вершине В;
4) составить уравнение высоты АК, проведенной из вершины А;
5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан);
6) сделать чертеж в системе координат.
Задача 2. Даны координаты точки А (3; 0), уравнение прямой l: 3x = 4
и число λ = 3 : 2.
Найти уравнение траектории точки М, которая движется в плоскости так, что отношение ее расстояний до точки А и до прямой l равно λ. Сделать чертеж в системе координат.
Задача 3. Дано уравнение кривой 2-го порядка: 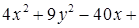
+ 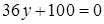 .
.
Привести заданное уравнение к каноническому виду путем параллельного переноса осей координат. Определить тип кривой, найти ее характерные элементы в исходной системе координат. Изобразить на чертеже расположение кривой относительно обеих систем координат.
Задача 4. Даны уравнение кривой 2-го порядка 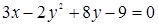
и уравнение прямой l: x +2y – 3 = 0.
Требуется:
1) привести заданное уравнение кривой 2-го порядка к каноническому виду;
2) найти точки пересечения кривой и заданной прямой;
3) построить обе линии в исходной системе координат.
Задача 5. Дано уравнение кривой в полярной системе координат (ПСК):
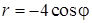 .
.
Требуется:
1) найти область определения функции 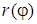 ;
;
2) построить кривую в ПСК, вычислив значения функции в точках 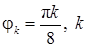 = 0, 1, ..., 16, принадлежащих области определения функции
= 0, 1, ..., 16, принадлежащих области определения функции 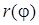 ;
;
3) найти уравнение заданной кривой в декартовой системе координат (ДСК), начало координат в которой совпадает с полюсом ПСК, а положительная полуось ОХ – с полярной осью ОР;
4) определить тип кривой.
Решение задачи 1
1) Вычислим длину стороны ВС по формуле (1):
|B С| = 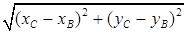 =
=
= 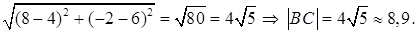
2) Составим уравнение стороны ВС, используя формулу (10):
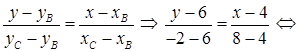
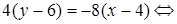
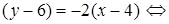 y = –2x + 14 – уравнение ВС.
y = –2x + 14 – уравнение ВС.
3) Внутренний угол треугольника при вершине В найдем как угол между прямыми ВА и ВС. Для этого сначала вычислим угловой коэффициент прямой ВА по формуле (9):
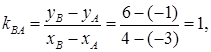
и возьмем из уравнения ВС угловой коэффициент прямой ВС: 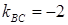 .
.
Из расположения точек A, B, C на координатной плоскости видно, что угол В в треугольнике ABC – острый, поэтому по формуле (13) вычислим
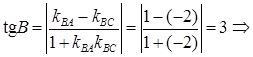
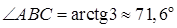 .
.
4) Для получения уравнения высоты А K, проведенной из вершины А, используем уравнение пучка прямых (8) и условие перпендикулярности прямых (12). Сначала вычислим угловой коэффициент прямой А K. Так как 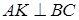 , то
, то 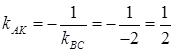 .
.
Уравнение AK получим по формуле (8):
у – уА = kAK(x– xA) 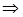 у – (–1) =
у – (–1) = 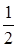 (x– (–3))
(x– (–3)) 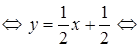
x –2y + 1 = 0 – уравнение AK.
5) Для определения координат центра тяжести треугольника используем свойство точки пересечения его медиан: если A М – медиана треугольника и P – точка пересечения его медиан, то P делит A М в отношении 2 : 1, начиная от точки А, т. е. 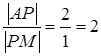 .
.
Основание медианы A М – точка М является серединой отрезка ВС. Найдем координаты точки М по формулам (3):
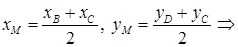
 М(6; 2).
М(6; 2).
Теперь, когда координаты концов отрезка A М известны, найдем координаты точки P, которая делит A М в отношении 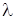 = 2, начиная
= 2, начиная
от точки А, по формулам деления отрезка в заданном отношении (2):
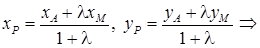
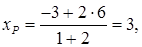
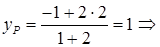
P (3; 1) – центр тяжести треугольника АВС.
6) Построим чертеж к задаче в системе координат ХО Y (рис. 11). Полученные при решении задачи результаты не противоречат чертежу.
 Ответы:
Ответы:
1) длина стороны |B С| = 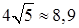 ;
;
2) уравнение стороны ВС:
y = –2x + 14;
3) угол при вершине В: 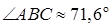 ;
;
4) уравнение высоты А K: x –2y +
+ 1 = 0;
5) координаты центра тяжести треугольника P (3; 1);
6) чертеж на рис. 11
Решение задачи 2
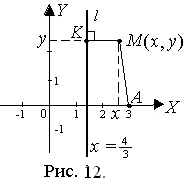 Пусть М (х; у) – произвольная точка на координатной плоскости, удовлетворяющую условию задачи (рис. 12), т. е.
Пусть М (х; у) – произвольная точка на координатной плоскости, удовлетворяющую условию задачи (рис. 12), т. е. 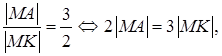 где K – основание перпендикуляра, опущенного из точки М на прямую 3x = 4. Так как K лежит
где K – основание перпендикуляра, опущенного из точки М на прямую 3x = 4. Так как K лежит
на прямой 3x = 4, то 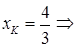 K
K 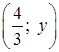 .
.
Запишем условие 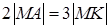 в координатной форме, используя формулу (1) для длины отрезка:
в координатной форме, используя формулу (1) для длины отрезка:
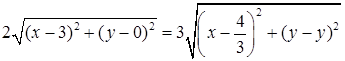 .
.
Это и есть уравнение искомой траектории, так как ему удовлетворяют координаты любой точки М (х; у) на этой траектории.
Для упрощения уравнения возведем обе части равенства в квадрат
и приведем подобные члены:
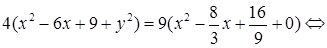
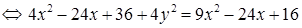
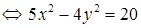 ,
,
откуда получаем
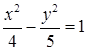 – уравнение гиперболы с полуосями
– уравнение гиперболы с полуосями
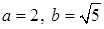 .
.
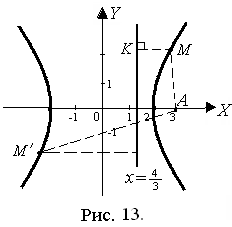 Построим чертеж гиперболы в системе координат ХО Y (рис. 13).
Построим чертеж гиперболы в системе координат ХО Y (рис. 13).
Ответ: 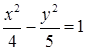 – уравнение траектории. Чертеж на рис. 13.
– уравнение траектории. Чертеж на рис. 13.
Решение задачи 3
Приведем заданное уравнение кривой 2-го порядка к каноническому виду. Для этого выделим в уравнении полные квадраты по переменным х и у:
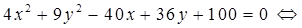
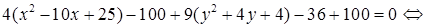
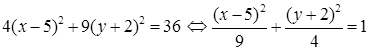 .
.
Получили уравнение эллипса с центром в точке O1(5; –2) (см. табл. 2
в разделе "справочный материал").
Осуществив параллельный перенос осей координат в системе XOY
по формулам: 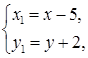 получим каноническое уравнение эллипса
получим каноническое уравнение эллипса 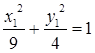 в системе координат X1O1Y1, где O1(5; –2) в системе XOY (рис. 14).
в системе координат X1O1Y1, где O1(5; –2) в системе XOY (рис. 14).
Найдем характерные элементы эллипса: 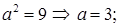
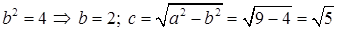 .
.
Отсюда получаем: а = 3 – большая полуось эллипса, b = 2 – малая полуось эллипса, с = 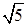 – фокусное расстояние. Координаты фокусов эллипса в системе координат X1O1Y1: F1(–
– фокусное расстояние. Координаты фокусов эллипса в системе координат X1O1Y1: F1(– 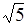 ; 0), F2(
; 0), F2( 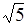 ; 0).
; 0).
Найдем координаты фокусов в системе координат XOY:
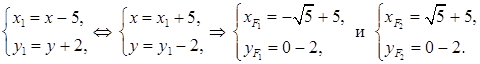
Таким образом, координаты фокусов эллипса в системе координат XOY:
F1(– 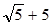 ; –2), F2(
; –2), F2( 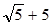 ;–2).
;–2).
Вычислим эксцентриситет эллипса: 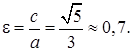
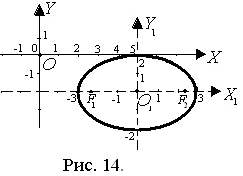 Изобразим на чертеже расположение эллипса относительно обеих систем координат (рис. 14).
Изобразим на чертеже расположение эллипса относительно обеих систем координат (рис. 14).
Ответ: 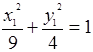 – каноническое уравнение эллипса, где
– каноническое уравнение эллипса, где 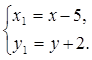
Характерные элементы:
– O1(5; –2) – центр эллипса;
– а = 3 – б большая полуось эллипса, b = 2 – малая полуось эллипса;
– с = 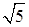 – фокусное расстояние;
– фокусное расстояние;
– координаты фокусов эллипса в системе координат XOY: F1(– 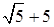 ; –2), F2(
; –2), F2( 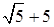 ; –2);
; –2);
– эксцентриситет эллипса 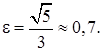
Чертеж на рис. 14.
Решение задачи 4
1) Приведем заданное уравнение кривой 2-го порядка к каноническому виду. Для этого выделим полный квадрат по переменной у (квадрат переменной х в уравнении отсутствует):
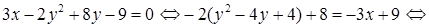
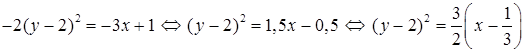 .
.
Получили уравнение параболы вида 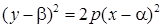 с вершиной
с вершиной
в точке 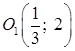 (см. табл. 2 в разделе "справочный материал"). Осуществим параллельный перенос осей координат по формулам:
(см. табл. 2 в разделе "справочный материал"). Осуществим параллельный перенос осей координат по формулам: 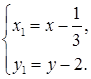
В результате получим каноническое уравнение параболы 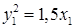 в системе координат X1O1Y1.
в системе координат X1O1Y1.
2) Найдем точки пересечения параболы и заданной прямой в системе координат XOY. Для этого решим систему уравнений:
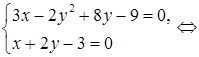
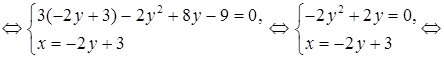
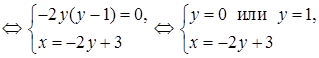
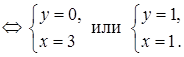
Таким образом, парабола и прямая пересекаются в точках А (3; 0)
и В (1; 1).
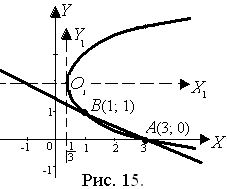 3) Построим обе линии в системе координат XOY (рис. 15).
3) Построим обе линии в системе координат XOY (рис. 15).
Ответы: 1) 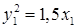 ;
;
2) А (3; 0), В (1; 1);
3) чертеж на рис. 15.
Решение задачи 5
1) Область определения функции 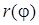 найдем из условия
найдем из условия 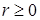 :
:
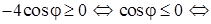
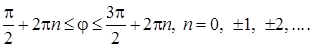
При n = 0 получаем 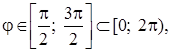 при
при 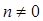 интервалы
интервалы 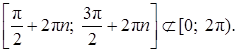 Следовательно, область определения
Следовательно, область определения 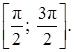
2) Для построения кривой в ПСК вычислим значения функции 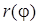
в точках 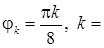 0, 1, …, 16, входящих в область определения, т. е.
0, 1, …, 16, входящих в область определения, т. е.
в точках, где выполнено условие 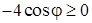 , и заполним табл. 3.
, и заполним табл. 3.
Таблица 3
| k | 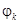
| 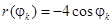
| k | 
| 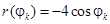
|
| 0 | 0 | – | – | – | – |
| 1 | π/8 | – | 9 | 9π/8 | 3,7 |
| 2 | 2π/8 | – | 10 | 10π/8 | 2,8 |
| 3 | 3π/8 | – | 11 | 11π/8 | 1,5 |
| 4 | 4π/8 | 0 | 12 | 12π/8 | 0 |
| 5 | 5π/8 | 1,5 | 13 | 13π/8 | – |
| 6 | 6π/8 | 2,8 | 14 | 14π/8 | – |
| 7 | 7π/8 | 3,7 | 15 | 15π/8 | – |
| 8 | 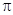
| 4 | 16 | 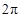
| – |
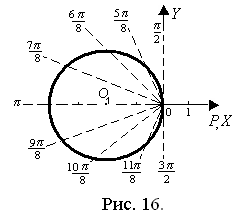 Для построения точек кривой в ПСК
Для построения точек кривой в ПСК
в каждом из направлений, задаваемых углом 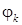 , откладываем от полюса отрезок длины
, откладываем от полюса отрезок длины 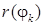 . Соединив полученные таким образом точки, получаем график функции
. Соединив полученные таким образом точки, получаем график функции 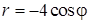 в ПСК (рис. 16).
в ПСК (рис. 16).
3) Найдем уравнение кривой, заданной в ПСК уравнением 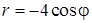 , в декартовой системе координат.
, в декартовой системе координат.
Если совместить ПСК и ДСК так, чтобы полюс совпал с началом координат ДСК, а ось ОР совпадала с положительной полуосью ОХ, то, используя формулы связи между декартовыми и полярными координатами точки 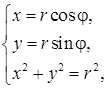 получим:
получим: 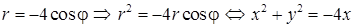 .
.
Следовательно, уравнение кривой 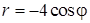 в ДСК имеет вид уравнения кривой 2-го порядка:
в ДСК имеет вид уравнения кривой 2-го порядка: 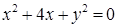 .
.
4) Для определения типа кривой выделим в уравнении полные квадраты по переменным х и у:
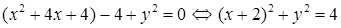 .
.
Это уравнение задает окружность с центром в точке O1(–2; 0) и с радиусом R = 2. Найдем координаты точки O1(–2; 0) в ПСК:
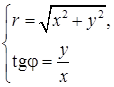
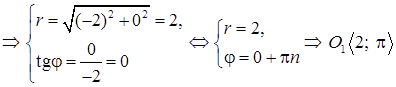 ,
,
(здесь выбираем n = 1, так как 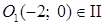 четверти (формулы (5)).
четверти (формулы (5)).
Ответы:
1) область определения: 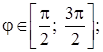
2) чертеж на рис. 16;
3) уравнение кривой в ДСК: 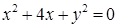 ;
;
4) тип кривой – окружность с центром в точке 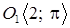 и с радиусом R = 2.
и с радиусом R = 2.
Справочный материал по темам
"Элементы линейной алгебры. Аналитическая
геометрия в пространстве"
Матрицы
Матрицей размерности m ´ n называется прямоугольная таблица, состоящая из m · n элементов (m строк и n столбцов):
Am´n = 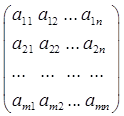 ,
,
где aij – элементы матрицы, i = 1, 2, …, m – номер строки, j = 1, 2, …,
n – номер столбца.
Для краткости матрицу обозначают одной буквой, например, буквой А.
Некоторые виды матриц:
1) нулевая матрица: матрица, все элементы которой равны нулю;
2) при n = 1 матрица-столбец: X = 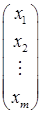 ;
;
3) при m = 1 матрица-строка: Y = 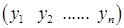 ;
;
4) при m = n квадратная матрица: An´n = 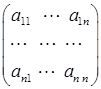 .
.
У квадратной матрицы различают главную диагональ (соединяющую элементы a11 и ann) и побочную диагональ.
Примеры квадратных матриц:
1) единичная матрица (квадратная матрица, на главной диагонали которой стоят единицы, а остальные элементы – нули):
E = 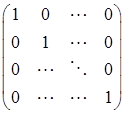 ;
;
2) квадратная матрица второго порядка: 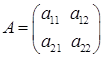 ;
;
3) квадратная матрица третьего порядка: 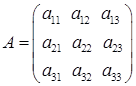 .
.
Две матрицы А и В называются равными, если они имеют одинаковые размерности и их соответствующие элементы равны:
Am ´ n = Bm ´ n Û aij = bij (i = 1, 2, …, m; j = 1, 2, …, n).
Определители
Определитель второго порядка (определитель квадратной матрицы второго порядка):
det A = 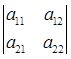 = a11 a22 – a12 a21. (24)
= a11 a22 – a12 a21. (24)
Определитель третьего порядка (определитель квадратной матрицы третьего порядка):
det A = 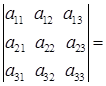
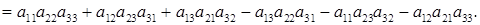 (25)
(25)
Для краткости определитель обозначают: | A | или Δ.
Минором элемента aij определителя называется определитель, который получается из исходного путем вычеркивания i-й строки и j-го столбца (обозначается Mij).
Алгебраическим дополнением элемента aij определителя (обозначается Aij) называется число:
Aij = (–1)i + j × Mij. (26)
Определитель третьего порядка можно вычислить, используя его разложение по 1-й строке:
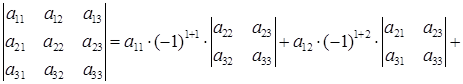
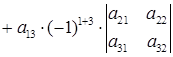 , (27)
, (27)
или, в краткой записи:
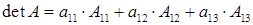 ,
,
т.е. определитель равен сумме произведений элементов первой строки
на их алгебраические дополнения. Аналогично можно записать разложение определителя по любой другой строке или столбцу.
4. Решение системы трех линейных алгебраических уравнений
с тремя неизвестными методом Крамера
Пусть дана система трех линейных алгебраических уравнений с тремя неизвестными 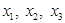 :
:
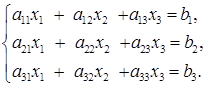 (28)
(28)
(коэффициенты aij и свободные члены bj для i = 1, 2, 3, j = 1, 2, 3 считаются заданными).
Тройка чисел 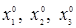 называется решением системы (28), если
называется решением системы (28), если
в результате подстановки этих чисел вместо 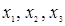 все три уравнения системы обращаются в тождества.
все три уравнения системы обращаются в тождества.
Систему (28) можно переписать в матричном виде:
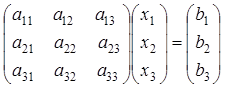 , или AX = B,
, или AX = B,
где A – это матрица коэффициентов при неизвестных, Х – столбец неизвестных, В – столбец свободных членов:
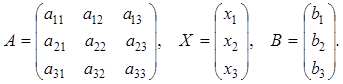
Составим определитель матрицы А и три вспомогательных определителя:
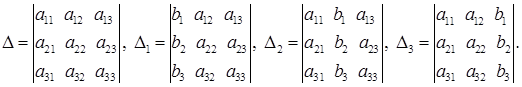 (29)
(29)
Определитель Δ называется главным определителем системы (28). Вспомогательные определители Δ1, Δ2 и Δ3 получаются из Δ заменой элементов соответственно первого, второго и третьего столбцов столбцом свободных членов.
Если определитель 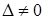 , то существует единственное решение системы (28) и оно выражается формулами:
, то существует единственное решение системы (28) и оно выражается формулами:
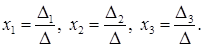 (30)
(30)
Формулы (30) называются формулами Крамера.
5. Решение системы трех линейных алгебраических уравнений
при помощи обратной матрицы
Присоединенной (союзной) матрицей к квадратной матрице
А = 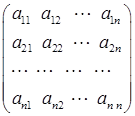 называется матрица
называется матрица
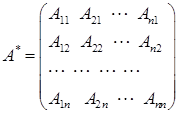 , (31)
, (31)
где 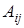 – алгебраические дополнения элементов
– алгебраические дополнения элементов 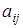 определителя матрицы А.
определителя матрицы А.
Матрица 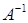 называется обратной к квадратной матрице А, если выполнено условие:
называется обратной к квадратной матрице А, если выполнено условие: 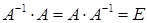 , где Е – единичная матрица той же размерности, что и А.
, где Е – единичная матрица той же размерности, что и А.
Обратная матрица существует тогда и только тогда, когда квадратная матрица А – невырожденная, т. е. 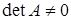 .
.
Чтобы найти обратную матрицу 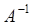 , необходимо:
, необходимо:
а) проверить невырожденность матрицы А, вычислив определитель detA;
б) найти союзную матрицу А* к матрице А;
в) найти обратную матрицу по формуле:
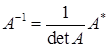 . (32)
. (32)
Если систему линейных алгебраических уравнений (28) переписать
в матричном виде AX = B, то ее решение можно получить матричным способом, т. е. при помощи обратной матрицы:
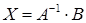 , (33)
, (33)
где 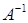 – обратная матрица для данной матрицы А.
– обратная матрица для данной матрицы А.
Решение задачи 1
Записываем матричный многочлен: 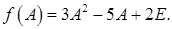 Здесь Е – единичная матрица той же размерности, что и А, т. е. 3-го порядка.
Здесь Е – единичная матрица той же размерности, что и А, т. е. 3-го порядка.
Найдем матрицу A2. При умножении матрицы A на себя используем правило "строка на столбец" (формула (23)):
A2 = A·A = 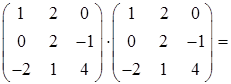
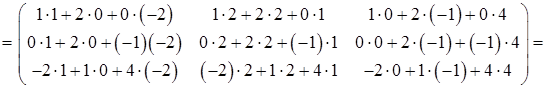
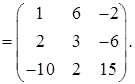
Найдем матрицу 2Е, используя правило умножения матрицы на число (формула (21)):
E = 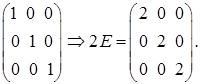
Теперь найдем значение матричного многочлена f(A), используя правило умножения матрицы на число и правило сложения матриц (формула (22)):
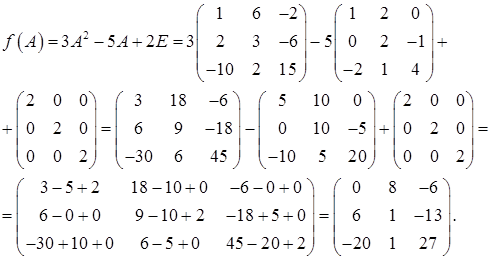
Ответ: 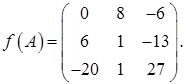
Решение задачи 2
1) Запишем систему в матричном виде:
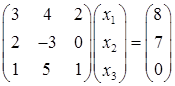 , или AX = B,
, или AX = B,
где 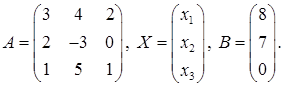
(Во втором уравнении системы отсутствует неизвестная х3, т. е. а23 = 0).
2) Решим систему с помощью формул Крамера. Для этого по формулам (29) составляем главный определитель системы из коэффициентов при неизвестных в левых частях уравнений и три вспомогательных определителя:
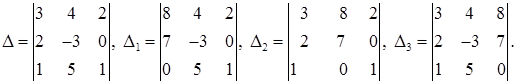
Вычислим эти определители, используя формулу (25):
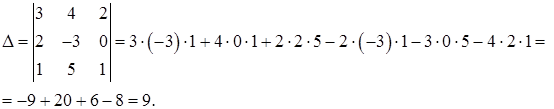
Так как ∆ ≠ 0, то данная система имеет единственное решение.
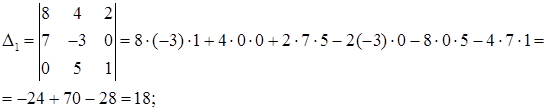
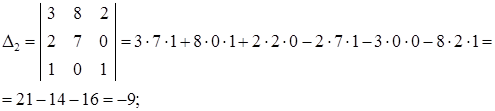
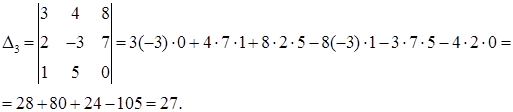
Найдем решение системы по формулам Крамера (30):
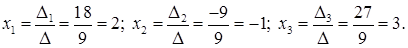
3) Решим систему при помощи обратной матрицы.
a) Определитель 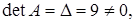 следовательно, обратная матрица существует.
следовательно, обратная матрица существует.
б) Чтобы найти союзную матрицу 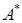 к матрице А, необходимо вычислить по формулам (26) алгебраические дополнения всех ее элементов:
к матрице А, необходимо вычислить по формулам (26) алгебраические дополнения всех ее элементов:
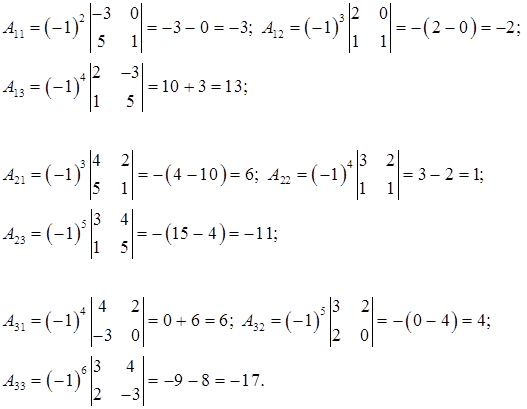
Здесь определители 2-го порядка вычислены по формуле (24).
Тогда союзная матрица (см. формулу (31)): 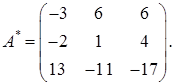
в) Найдем обратную матрицу по формуле (32):
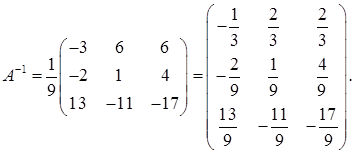
г) Получим решение системы при помощи обратной матрицы по формуле (33) (правило "строка на столбец"):
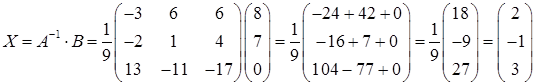
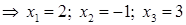 .
.
Решение, полученное матричным способом, совпадает с тем, которое получено по формулам Крамера, что подтверждает правильность этого решения.
Ответы:
1) система в матричном виде: AX = B, где
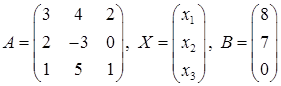 ;
;
2) решение системы, полученное с помощью формул Крамера:
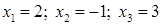 ;
;
3) решение системы, полученное при помощи обратной матрицы:
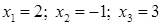 .
.
Решение задачи 3
1) Модуль вектора 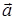 вычисляется по формуле (35):
вычисляется по формуле (35):
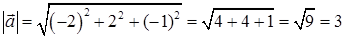 .
.
2) Чтобы найти координаты вектора 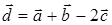 , используем формулы (38) и (39):
, используем формулы (38) и (39):
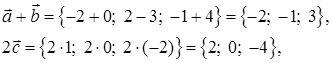
тогда 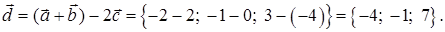
3) Косинус угла между векторами 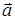 и
и 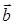 найдем по формуле (41):
найдем по формуле (41):
 .
.
Для этого вычислим скалярное произведение 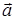 и
и 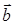 по формуле (40):
по формуле (40): 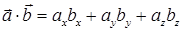 = –2∙0 + 2∙(–3) + (–1)∙4 = –10, затем модуль вектора
= –2∙0 + 2∙(–3) + (–1)∙4 = –10, затем модуль вектора 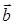 :
:
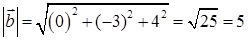 , тогда
, тогда 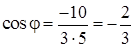
и 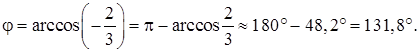
4) Проекцию вектора 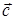 на направление
на направление 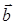 вычислим по формуле (42):
вычислим по формуле (42):
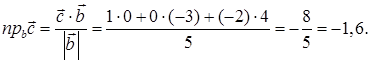
5) Площадь треугольника, построенного на векторах 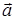 и
и 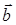 найдем по формуле (44). Для этого сначала находим векторное произведение этих векторов по формуле (43):
найдем по формуле (44). Для этого сначала находим векторное произведение этих векторов по формуле (43):
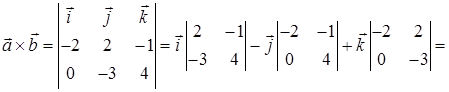
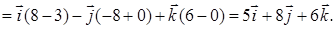
Следовательно, площадь треугольника, построенного на векторах 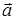 и
и 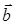 :
:
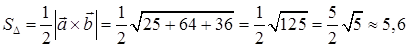 (кв. ед.).
(кв. ед.).
6) Для вычисления объема параллелепипеда, построенного на векторах 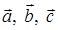 находим смешанное произведение векторов по формуле (45):
находим смешанное произведение векторов по формуле (45):
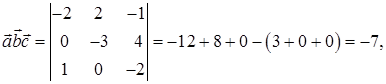
тогда объема параллелепипеда по формуле (47): 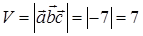 .
.
Ответы:
1) модуль вектора 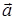 :
: 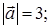
2) координаты вектора 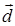 :
: 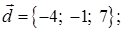
3) угол между векторами 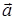 и
и 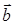 :
: 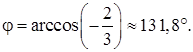
4) проекция вектора 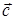 на направление вектора
на направление вектора 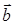 :
: 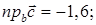
5) площадь треугольника, построенного на векторах 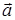 и
и 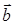 :
: 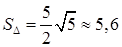 (кв. ед.);
(кв. ед.);
6) объем параллелепипеда, построенного на векторах 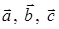 :
:
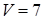 (куб. ед.).
(куб. ед.).
Решение задачи 4
1) Длину ребра 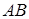 найдем по формуле (36):
найдем по формуле (36):
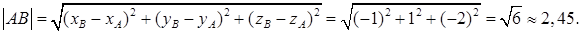
2) Чтобы получить уравнение плоскости грани ABC, необходимо найти вектор, перпендикулярный плоскости ABC, т. е. вектор, перпендикулярный векторам 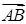 и
и 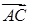 . Одним из таких векторов является векторное произведение
. Одним из таких векторов является векторное произведение 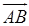 на
на 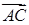 . Для того, чтобы найти его, сначала вычислим координаты векторов по формуле (37):
. Для того, чтобы найти его, сначала вычислим координаты векторов по формуле (37):
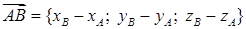 = {–3–(–2); 2–1; –1–1} = {–1; 1; –2},
= {–3–(–2); 2–1; –1–1} = {–1; 1; –2},
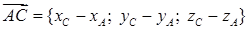 = {7; –3; –3}.
= {7; –3; –3}.
Векторное произведение 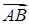 и
и 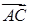 найдем по формуле (43):
найдем по формуле (43):
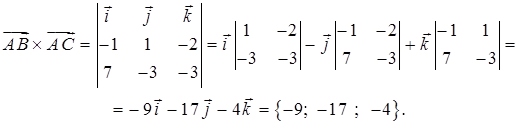
В качестве вектора нормали к плоскости ABC можно взять любой вектор, коллинеарный полученному, например, 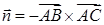 = {9; 17; 4}. Используем уравнение плоскости, проходящей через точку
= {9; 17; 4}. Используем уравнение плоскости, проходящей через точку 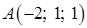 перпендикулярно вектору
перпендикулярно вектору 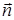 (формула (48):
(формула (48): 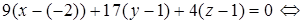
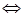
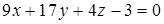 – уравнение плоскости грани ABC .
– уравнение плоскости грани ABC .
3) Прежде, чем найти угол 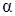 между гранями ABC и BCD, получим уравнение грани BCD, используя уравнение плоскости, проходящей через три заданные точки
между гранями ABC и BCD, получим уравнение грани BCD, используя уравнение плоскости, проходящей через три заданные точки 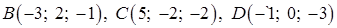 (формула (49):
(формула (49):
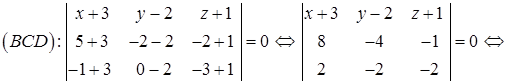
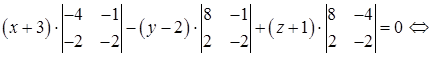
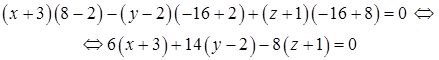
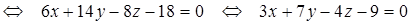 – уравнение грани BCD.
– уравнение грани BCD.
Из уравнения плоскости BCD возьмем координаты вектора нормали 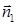 , перпендикулярного этой плоскости:
, перпендикулярного этой плоскости: 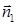 ={3; 7; –4}.
={3; 7; –4}.
Косинус угла 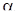 между плоскостями (гранями) ABC и BCD найдем
между плоскостями (гранями) ABC и BCD найдем
по формуле(50):
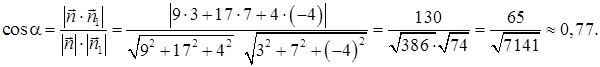
Отсюда 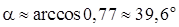 .
.
4) Уравнения ребра AB можно записать как параметрические уравнения прямой, проходящей через точку A(–2; 1; 1) и имеющей направляющий вектор 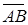 = {–1; 1; –2} (формулы (51)):
= {–1; 1; –2} (формулы (51)):
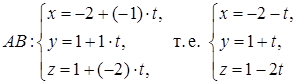 – параметрические уравнения AB.
– параметрические уравнения AB.
Другой способ: можно использовать уравнения прямой, проходящей через две точки 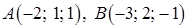 (формулы (53)):
(формулы (53)):
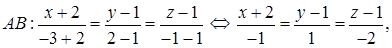
откуда, обозначив каждую из дробей t, получаем:
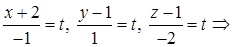
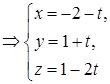 – параметрические уравнения AB.
– параметрические уравнения AB.
5) Высота пирамиды DK – это прямая, проведенная из вершины D перпендикулярно грани ABC. Она имеет направляющий вектор 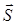 , коллинеарный вектору нормали плоскости ABC. Можно взять, например,
, коллинеарный вектору нормали плоскости ABC. Можно взять, например, 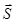 =
= 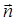 = {9; 17; 4}. Запишем канонические уравнения высоты DK, используя точку D(–1; 0; –3)
= {9; 17; 4}. Запишем канонические уравнения высоты DK, используя точку D(–1; 0; –3)
и вектор 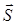 = {9; 17; 4} (формулы (52)):
= {9; 17; 4} (формулы (52)):
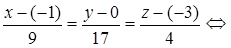
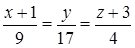 – канонические уравнения DK.
– канонические уравнения DK.
6) Прежде, чем найти точку пересечения DK и грани ABC, получим параметрические уравнения прямой DK. Обозначив каждую из дробей
в канонических уравнениях буквой t, получаем:
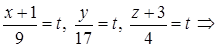
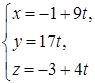 – параметрические уравнения DK.
– параметрические уравнения DK.
Точка пересечения DK и грани ABC (точка К) лежит на прямой, а значит, имеет координаты 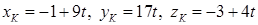 , и принадлежит плоскости, т. е. ее координаты удовлетворяют уравнению плоскости ABC. Поэтому координаты точки K найдем, решив систему:
, и принадлежит плоскости, т. е. ее координаты удовлетворяют уравнению плоскости ABC. Поэтому координаты точки K найдем, решив систему:
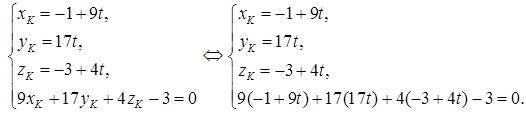
Решим последнее уравнение относительно t:
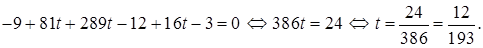
Вычислим координаты точки K, подставив найденное значение параметра в первые три уравнения системы:
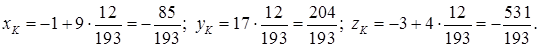
Итак, точка пересечения DK и грани ABC: 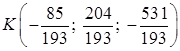 .
.
7) Угол 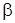 между ребрами AB и BC найдем, как угол между на-
между ребрами AB и BC найдем, как угол между на-
правляющими векторами прямых AB и BC: 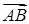 = {–1; 1; –2}
= {–1; 1; –2}
и 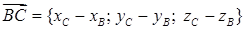 = {8; –4; –1}. Найдем косинус угла
= {8; –4; –1}. Найдем косинус угла 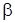
по формуле(54):
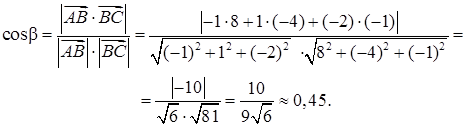
Тогда угол между ребрами AB и BC: 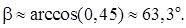
8) Чтобы определить угол  между ребром AD и гранью ABC, найдем направляющий вектор прямой:
между ребром AD и гранью ABC, найдем направляющий вектор прямой: 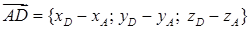 = {1; –1; –4}. Плоскость ABC имеет вектор нормали
= {1; –1; –4}. Плоскость ABC имеет вектор нормали 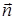 = {9; 17; 4}. Синус угла
= {9; 17; 4}. Синус угла 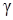 между прямой
между прямой 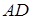 и плоскостью ABC можно вычислить по формуле (55):
и плоскостью ABC можно вычислить по формуле (55):
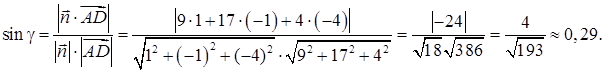
 |
Тогда угол между ребром AD и гранью ABC:
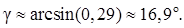
9) Выполним чертеж пирамиды в системе координат (рис. 19).
Ответы:
1) 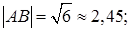
2) АВС: 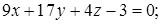
3) 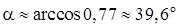 ;
;
4) 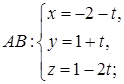
5) DK: 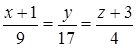 ;
;
6) 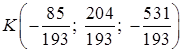 ;
;
7) 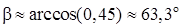 ;
;
8) 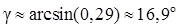 ;
;
9) чертеж пирамиды на рис. 19.
Варианты контрольнЫХ работ
Каждый вариант контрольной работы № 1 для студентов-заочников
1 курса всех специальностей содержит 5 задач, охватывающих материал по теме "Аналитическая геометрия на плоскости". Каждый вариант контрольной работы № 2 содержит 4 задачи по темам "Элементы линейной алгебры. Аналитическая геометрия в пространстве".
Перед выполнением каждой контрольной работы студенту необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии с методическими указаниями, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы.
Задания для всех вариантов общие; студенту следует выбрать из условия каждой задачи данные, необходимые для ее решения, в соответствии со своим вариантом. Оформление контрольных работ должно соответствовать установленным правилам и требованиям. Необходимые чертежи должны выполняться четко, с соответствующими подписями и комментариями (см. образец выполнения примерного варианта работы).
Варианты контрольной работы № 1
Задача 1. Даны координаты вершин треугольника АВС.
| Номер варианта | Координаты точек | Номер варианта | Координаты точек |
| 1 | А(–2; –3), В(2; 7), С(6; –1) | 6 | А(3; –3), В(–4; 1), С(–2; 5) |
| 2 | А(–5; 1), В(6; 3), С(–4; –7) | 7 | А(3; 5), В(–2; 2), С(2; –4) |
| 3 | А(4; 5), В(–3; 2), С(5; –4) | 8 | А(–2; 4), В(5; 6), С(3; –4) |
| 4 | А(7; –7), В(1; 2), С(–5; –4) | 9 | А(3; 7), В(–4; 1), С(–2; –5) |
| 5 | А(–3; 4), В(4; 5), С(8; –3) | 10 | А(4; 3), В(–3; –2), С(–7; 2) |
Требуется:
1) вычислить длину стороны ВС;
2) составить уравнение стороны ВС;
3) найти внутренний угол треугольника при вершине В;
4) составить уравнение высоты АК, проведенной из вершины А;
5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан);
6) сделать чертеж в системе координат.
Задача 2. Даны координаты точки А, уравнение прямой l и число λ.
| Номер варианта | Координаты точки | Уравнение прямой l | Число λ | Номер варианта | Координаты точки | Уравнение прямой l | Число λ |
| 1 | А(–1; 0) | y + 2 = 0 | 1 : 1 | 6 | А(–5; 1) | x + 1 = 0 | 1: 1 |
| 2 | А(3; 1) | 3x = 16 | 3 : 4 | 7 | А(5; –4) | 5x = 1 | 5 : 1 |
| 3 | А(3; 0) | x = 0 | 2 : 1 | 8 | А(1; 0) | 2x = 7 | 2 : 3 |
| 4 | А(2; 0) | 4x = 1 | 4 : 3 | 9 | А(1; 2) | x = 4 | 1 : 2 |
| 5 | А(0; 0) | 2x + 5 = 0 | 2 : 3 | 10 | А(3; 2) | 3x = 1 | 3 : 1 |
Найти уравнение траектории точки М, которая движется в плоскости так, что отношение ее расстояний до точки А и до прямой l равно λ. Сделать чертеж в системе координат.
Задача 3. Дано уравнение кривой 2-го порядка.
| Номер варианта | Уравнение кривой | Номер варианта | Уравнение кривой |
| 1 | 7x2 – 9y2 + 42x+ 18y – 9 = 0 | 6 | 9x2 + 4y2 – 54x + 8y + 49 = 0 |
| 2 | x2 + 2x – 12y + 37 = 0 | 7 | x2 – 10x + 4y + 17 = 0 |
| 3 | 5x2 + 9y2 + 10x – 54y + 41 = 0 | 8 | 3x2 – y2 – 30x – 2y + 62 = 0 |
| 4 | y2 + 6x + 6y – 3 = 0 | 9 | y2 – 8x – 4y – 4 = 0 |
| 5 | 5x2 – 4y2 – 20x – 24y – 36 = 0 | 10 | 7x2 + 16y2 – 56x + 64y + 64 = 0 |
Привести заданное уравнение к каноническому виду путем параллельного переноса осей координат. Определить тип кривой, найти ее характерные элементы в исходной системе координат. Изобразить на чертеже расположение кривой относительно обеих систем координат.
Задача 4. Даны уравнение кривой 2-го порядка и уравнение прямой.
| Номер варианта | Уравнение кривой | Уравнение прямой |
| 1 | x2 + 2y2 – 2x + 8y + 3 = 0 | x + 2y + 3 = 0 |
| 2 | x2 – 2y2 + 4x + 4y – 6 = 0 | x + 2y = 0 |
| 3 | x2 + 6x – 16y + 25 = 0 | x – 4y + 15 = 0 |
| 4 | x2 + 4y2 – 6x + 8y + 5 = 0 | x – 2y – 5 = 0 |
| 5 | y2 – 4x – 6y – 15 = 0 | 2x + y – 3 = 0 |
| 6 | x2 – 5y2 + 10x + 20y – 15 = 0 | x – 5y + 15 = 0 |
| 7 | x2 + 4y2 + 2x – 32y + 45 = 0 | x – y + 5 = 0 |
| 8 | x2 – 4x + 8y + 44 = 0 | x – 2y – 20 = 0 |
| 9 | 2x2 – y2 – 16x – 6y + 19 = 0 | x – y – 7 = 0 |
| 10 | y2 + 10x + 8y – 34 = 0 | 2x + y + 4 = 0 |
Требуется:
1) привести заданное уравнение кривой 2-го порядка к каноническому виду;
2) найти точки пересечения кривой и заданной прямой;
3) построить обе линии в исходной системе координат.
Задача 5. Дано уравнение кривой в полярной системе координат (ПСК).
| Номер варианта | Уравнение кривой | Номер варианта | Уравнение кривой |
| 1 | 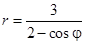
| 6 | 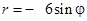
|
| 2 | 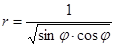
| 7 | 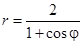
|
| 3 | 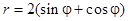
| 8 | 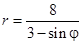
|
| 4 | 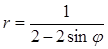
| 9 | 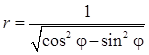
|
| 5 | 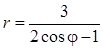
| 10 | 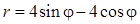
|
Требуется:
1) найти область определения функции 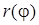 ;
;
2) построить кривую в ПСК, вычислив значения функции в точках 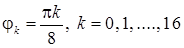 , принадлежащих области определения функции
, принадлежащих области определения функции 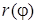 ;
;
3) найти уравнение заданной кривой в декартовой системе координат (ДСК), начало координат в которой совпадает с полюсом ПСК, а положительная полуось ОХ – с полярной осью ОР;
4) определить тип кривой.
Варианты контрольной работы № 2
Задача 1. Даны многочлен f(x) и матрица А.
| Номер варианта | Многочлен f ( x ) | Матрица А |
| 1 | 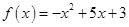
| 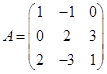
|
| 2 | 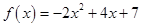
| 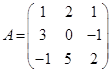
|
Окончание таблицы
| Номер варианта | Многочлен f ( x ) | Матрица А |
| 3 | 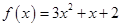
| 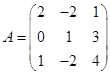
|
| 4 | 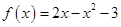
| 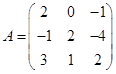
|
| 5 | 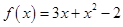
| 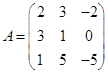
|
| 6 | 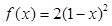
| 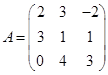
|
| 7 | 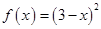
| 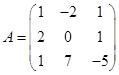
|
| 8 | 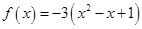
| 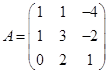
|
| 9 | 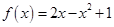
| 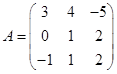
|
| 10 | 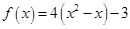
| 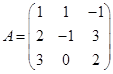
|
Требуется найти значение матричного многочлена 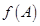 .
.
Задача 2. Дана система трех линейных алгебраических уравнений
с тремя неизвестными.
| Номер варианта | Система уравнений | Номер варианта | Система уравнений |
| 1 | 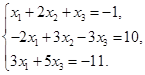
| 6 | 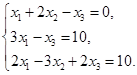
|
| 2 | 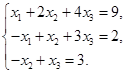
| 7 | 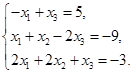
|
| 3 | 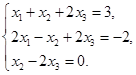
| 8 | 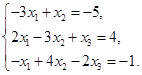
|
| 4 | 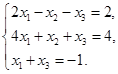
| 9 | 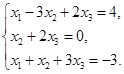
|
| 5 | 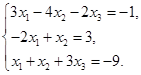
| 10 | 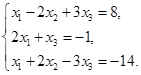
|
Требуется:
1) записать систему в матричном виде;
2) найти решение системы с помощью формул Крамера;
3) решить систему при помощи обратной матрицы.
Задача 3. Даны координаты трех векторов 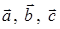 и вектор
и вектор 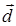 .
.
| Номер варианта | Векторы 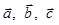
| Вектор 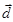
|
| 1 | 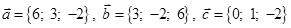
| 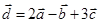
|
| 2 | 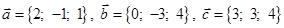
| 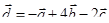
|
| 3 | 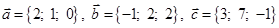
| 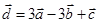
|
Окончание таблицы
| Номер варианта | Векторы 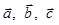
| Вектор 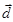
|
| 4 | 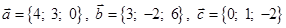
| 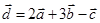
|
| 5 | 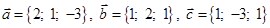
| 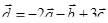
|
| 6 | 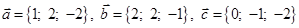
| 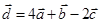
|
| 7 | 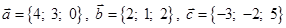
| 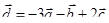
|
| 8 | 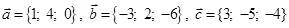
| 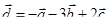
|
| 9 | 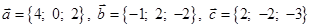
| 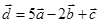
|
| 10 | 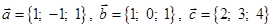
| 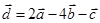
|
Требуется:
1) вычислить модуль вектора 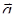 ;
;
2) найти координаты вектора 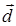 ;
;
3) найти угол φ между векторами 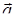 и
и 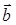 ;
;
4) вычислить проекцию вектора 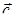 на направление вектора
на направление вектора 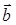 ;
;
5) вычислить площадь треугольника, построенного на векторах 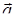 и
и 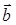 ;
;
6) вычислить объем параллелепипеда, построенного на векторах 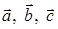 .
.
Задача 4. Даны координаты точек – вершин пирамиды ABCD.
| Номер варианта | Координаты точек |
| 1 | А(1; 2; –1), В(0; 0; 1), С(1; –3; 3), D(2; –1; –1) |
| 2 | А(7; 2; 4), В(7; –1; –2), С(3; 3; 1), D(4; 2; 1) |
| 3 | А(1; 3; 6), В(2; 2; 1), С(–1; 0; 1), D(–4; 6; –3) |
| 4 | А(–2; 0; –4), В(–1; 7; 1), С(4; –8; –4), D(1; –4; 6) |
| 5 | А(1; 2; 0), В(3; 0; –1), С(5; –2; 3), D(3; 2; –1) |
| 6 | А(–1; 1; 2), В(2; 1; –2), С(–2; 0; 4), D(2; –1; 2) |
| 7 | А(4; 2; 5), В(2; –3; 0), С(–10; 5; 8), D(–5; 2; 4) |
| 8 | А(2; –1; 1), В(–1; –3; 2), С(–2; 3; 1), D(–1; 2; –3) |
| 9 | А(–1; 1; 2), В(–2; 0; 3), С(3; 6; –3), D(–1; –2; 7) |
| 10 | А(4; –1; 3), В(–2; 1; 0), С(0; –5; 1), D(–2; 1; –1) |
Требуется:
1) вычислить длину ребра AB;
2) найти уравнение плоскости грани ABC;
3) найти угол 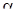 между гранями ABC и BCD;
между гранями ABC и BCD;
4) составить параметрические уравнения прямой AB;
5) составить канонические уравнения высоты пирамиды DK, проведенной из вершины D;
6) найти координаты точки пересечения DK и грани ABC;
7) найти угол 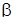 между ребрами AB и BC;
между ребрами AB и BC;
8) найти угол 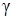 между ребром AD и гранью ABC;
между ребром AD и гранью ABC;
9) сделать чертеж пирамиды в системе координат.
Рекомендуемая литература
1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. – М. : Айрис-пресс, 2003. – 288 с.
2. Щипачев, В.С. Высшая математика : учебник для вузов / В.С. Щипачев.– М. : Высш. шк., 1998. – 479 с.
3. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 1
/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М. : Высш. шк., 1999. – 304 с.
4. Щипачев, В.С. Задачник по высшей математике / В.С. Щипачев. – М. : Высш. шк., 2001. – 304 с.
Налоговая льгота – Общероссийский классификатор продукции
ОК 005-93, т. 2; 95 3004 – воспитательная, образовательная и педагогическая литература

Издательство МГТУ. 183010 Мурманск, Спортивная, 13.
Сдано в набор 14.09.2007. Подписано в печать 18.09.2007. Формат 60´841/16.
Бум. типографская. Усл. печ. л. 2,79. Уч.-изд. л. 2,18. Заказ 443. Тираж 300 экз.
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ
Федеральное государственное образовательное учреждение высшего профессионального образования
"Мурманский государственный технический университет"
Аналитическая геометрия
на плоскости.
Элементы линейной алгебры.
Аналитическая геометрия
в пространстве
Часть 1
Мурманск
2007
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ
Федеральное государственное образовательное учреждение высшего профессионального образования
"Мурманский государственный технический университет"
Кафедра высшей математики
и программного обеспечения ЭВМ
Аналитическая геометрия на плоскости.
Элементы линейной алгебры.
Аналитическая геометрия в пространстве
Часть 1
Методические рекомендации к выполнению контрольных
работ по дисциплине "Математика"
для студентов I курса вечерне-заочного факультета
Мурманск
2007
УДК 514.2 + 512.64 + 514.144.2 (075.8)
ББК 22.151.5 + 22.143 Я73
М 33
Составители: Л.Г. Мостовская, доцент кафедры высшей математики
и программного обеспечения ЭВМ Мурманского государственного технического университета;
Е.Е. Великая, ст. преподаватель той же кафедры
Методические рекомендации рассмотрены и одобрены кафедрой
15 февраля 2006 г., протокол № 4
Рецензент - В.С. Кацуба, канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ
Оригинал-макет подготовлен в авторской редакции
Электронная верстка Т.В. Бекреневой
Ó Мурманский государственный
технический университет, 2007
Оглавление
Введение.. 4
Методические указания к изучению тем "Аналитическая геометрия на плоскости" И "Элементы линейной алгебры. Аналитическая геометрия в пространстве". 5
Справочный материал по теме
"Аналитическая геометрия на плоскости". 6
1. Декартова система координат (ДСК) на плоскости. 6
2. Полярная система координат (ПСК) 7
3. Прямая линия на плоскости. 7
4. Кривые второго порядка. 8
Примерный вариант и образец выполнения
контрольной работы № 1. 11
Справочный материал по темам
"Элементы линейной алгебры.
Аналитическая геометрия в пространстве". 19
1. Матрицы.. 19
2. Линейные операции над матрицами. 20
3. Определители. 21
4. Решение системы трех линейных алгебраических уравнений
с тремя неизвестными методом Крамера. 22
5. Решение системы трех линейных алгебраических уравнений
при помощи обратной матрицы.. 23
6. Векторы. Операции над векторами. 24
7. Уравнение плоскости в пространстве. 27
8. Уравнения прямой в пространстве. 27
Примерный вариант и образец выполнения
контрольной работы № 2. 28
Варианты контрольнЫХ работ. 39
Варианты контрольной работы № 1. 39
Варианты контрольной работы № 2. 41
Рекомендуемая литература.. 45
Введение
Основной формой обучения студентов-заочников математике является самостоятельная работа студентов, которая включает изучение теоретического материала, решение типовых задач с проверкой правильности решения, выполнение контрольных работ.
В настоящих рекомендациях содержатся краткие теоретические сведения, рекомендации к выполнению контрольной работы 1 по теме "Аналитическая геометрия на плоскости" и контрольной работы 2 по теме "Элементы линейной алгебры. Аналитическая геометрия в пространстве", список литературы.
В результате изучения указанных тем студенты I курса должны:
• освоить метод координат на плоскости и научиться решать простые геометрические задачи с использованием уравнений прямой и уравнений кривых второго порядка;
• ознакомиться с основами линейной алгебры (действия над матрицами, вычисление определителей), научиться решать системы линейных алгебраических уравнений методом Крамера и с помощью обратной матрицы;
• знать основы векторной алгебры (линейные операции над векторами, скалярное, векторное и смешанное произведения векторов и их приложения);
• освоить метод координат в пространстве, научиться решать задачи
с использованием средств аналитической геометрии.
В предлагаемых методических рекомендациях даны варианты контрольных работ, справочный материал, необходимый для их выполнения,
а также примеры решения контрольных работ.
Методические указания к изучению тем
"Аналитическая геометрия на плоскости"
И "Элементы линейной алгебры.
Аналитическая геометрия в пространстве"
В таблице приведены наименования тем в соответствии с содержанием контрольных работ и необходимая литература. Перед выполнением контрольных работ рекомендуется изучить соответствующий теоретический материал и решить указанные в таблице задачи.
Таблица 1
| Номер конт-рольной работы | Номер задачи | Наименования тем | Литература |
| 1 | 1 | Декартовы координаты точек на плоскости. Расстояние между двумя точками на плоскости. Деление отрезка в данном отношении. Уравнения прямой линии на плоскости. Условия параллельности и перпендикулярности прямых на плоскости | [1], гл. III, § 9.1, 9.2, 10.1, 10.2, 10.3; [2], гл. 3, § 1 - 2, 5, 6; [3], ч. 1, гл.I, № 16 - 20, 74, 76, 99, 100, 102, 105, 111 - 114, 119, 121; [4], гл. 3, № 21, 24, 25, 29, 39, 86 - 88, 91, 94, 95, 122 |
| 1 | 2 | Уравнения линий на плоскости в декартовых координатах | [1], гл. III, § 10.1; [2], гл. 3, § 5; [3], ч. 1, гл. I, № 44, 47, 48, 150; [4], гл. 3, № 52, 55, 60 - 67, 136, 148, 159 |
| 1 | 3, 4 | Кривые второго порядка: окружность, эллипс, гипербола, парабола. Приведение уравнения второго порядка к каноническому виду. Точки пересечения линий на плоскости | [1], гл. III, § 9.3, 11; [2], гл. 3, § 7, 8; [3], ч. 1, гл. I, № 134, 136, 144, 145, 149, 155 - 157, 169, 170, 187 - 195; [4], гл. 3, № 126, 128, 139, 141, 150 - 152, 156 |
| 1 | 5 | Полярные координаты точки на плоскости. Связь между декартовыми и полярными координатами. Уравнения линий на плоскости в полярных координатах | [1], гл. III, § 9.1, 10.1; [2], гл. 3, § 3, 5; [3], ч. 1, гл. I, № 29, 30, 33 - 35, 49 - 51; [4], гл. 3, № 44, 45, 53(5), 54 |
| 2 | 1 | Матрицы. Операции над матрицами | [1], гл. I, § 1; [2], гл. 10, § 1; [3], ч. 1, гл. IV, № 399 - 403, 414, 415 |
| 2 | 2 | Определители. Обратная матрица. Решение систем линейных алгебраических уравнений по формулам Крамера и с помощью обратной матрицы | [1], гл. I, § 2, 3.1, 3.2, 4.1, 4.3; [2], гл. 10, § 2 - 4; [3], ч. 1, гл. I, № 210, 211, 217, 219, 225 - 227; [4], гл. 7, № 20 - 25, 38 - 43 |
Окончание табл. 1
| Номер конт-рольной работы | Номер задачи | Наименования тем | Литература |
| 2 | 3 | Линейные операции над векторами. Скалярное, векторное, смешанное произведения векторов | [1], гл. II, § 5 - 8; [2], гл. 9, § 1 - 4, 6 - 8; [3], ч. 1, гл. II, № 244, 248, 256 - 266, 284; [4], гл. 10, № 37, 47, 48, 51, 72, 73, 77, 83 - 84 |
| 2 | 4 | Плоскость и прямая линия в пространстве | [1], гл. IV, § 12.1 - 12.6; [2], гл. 9, § 11 - 13; [3], ч. 1, гл. III, № 288, 289, 302, 307, 314, 325, 333, 334, 341; [4], гл. 10, № 104, 113, 119, 131, 132, 141, 151, 153 |
Примечание. Ссылки на литературу в таблице даны в соответствии
с номерами в списке рекомендуемой литературы.
Справочный материал по теме
"Аналитическая геометрия на плоскости"
Декартова система координат (ДСК) на плоскости
Расстояние |АВ| между двумя точками А(хА; уА) и В(хВ; уВ) (рис. 1):
|AB| = 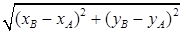 . (1)
. (1)
Деление отрезка в заданном отношении. Если точка С делит отрезок АВ в отношении λ, начиная от точки A (рис. 1),
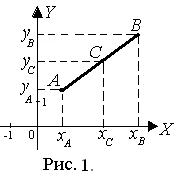 т. е.
т. е. 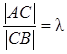 , то координаты точки C:
, то координаты точки C:
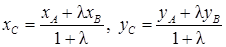 . (2)
. (2)
Если точка С делит отрезок АВ пополам,
т.е. 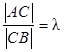 =1, то координаты точки C:
=1, то координаты точки C:
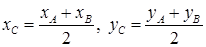 . (3)
. (3)
В ДСК уравнение линии имеет вид F(х, у) = 0 или у = f(х).
Дата: 2018-12-28, просмотров: 363.
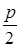 ), уравнение директрисы:
), уравнение директрисы: