Умножение матрицы A на число k:

B = k × A = ,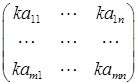

или, в краткой записи:

B = k × A Û b_ij = k × a_ij (i = 1, 2, …, m; j = 1, 2, …, n).               (21)

Сложение (вычитание) матриц A и B одинаковой размерности:

C_{m ´ n} = A_{m ´ n} ± B_{m ´ n} Û c_ij = a_ij ± b_ij (i = 1, 2, …, m; j = 1, 2, …, n).   (22)

Произведение матриц A_{m ´ n} и B_{n ´ k}:

C_m´k = A_m´n × B_n´k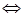

c_ij = a_i1b_1j + a_i2b_2j + ¼ + a_inb_nj (i = 1, 2, …, m; j = 1, 2, …, k).        (23)

Формулу (23) легко запомнить, как правило умножения "строка
на столбец": произведение матриц A_m´n и B_n´k есть матрица C_m´k, у которой элемент c_ij равен сумме произведений соответствующих элементов i-й строки матрицы A и j-го столбца матрицы В.

Замечание. Перемножать можно только соответственные матрицы А и В, т. е. число столбцов матрицы А должно быть равно числу строк матрицы В.

Если задан многочлен 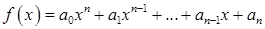, то матричным многочленом  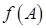называется выражение

,

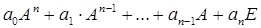где А – квадратная матрица, 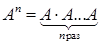 и Е – единичная матрица той же размерности, что и А. Значением матричного многочлена является матрица.

Определители

Определитель второго порядка (определитель квадратной матрицы второго порядка):

det A = 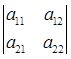= a₁₁ a₂₂ – a₁₂ a₂₁.                           (24)

Определитель третьего порядка (определитель квадратной матрицы третьего порядка):

det A =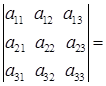

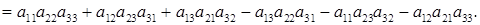(25)

Для краткости определитель обозначают: | A | или Δ.

Минором элемента a_ij определителя называется определитель, который получается из исходного путем вычеркивания i-й строки и j-го столбца (обозначается M_ij).

Алгебраическим дополнением элемента a_ij определителя (обозначается A_ij) называется число:

A_ij = (–1)^{i + j} × M_ij.                                        (26)

Определитель третьего порядка можно вычислить, используя его разложение по 1-й строке:

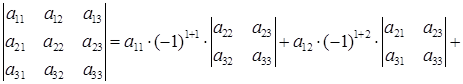
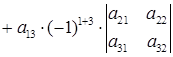,                               (27)

или, в краткой записи:

,

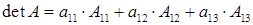т.е. определитель равен сумме произведений элементов первой строки
на их алгебраические дополнения. Аналогично можно записать разложение определителя по любой другой строке или столбцу.

4. Решение системы трех линейных алгебраических уравнений
с тремя неизвестными методом Крамера

Пусть дана система трех линейных алгебраических уравнений с тремя неизвестными :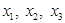

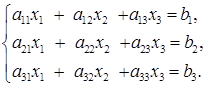                                 (28)

(коэффициенты a_ij и свободные члены b_j для i = 1, 2, 3, j = 1, 2, 3 считаются заданными).

Тройка чисел 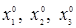  называется решением системы (28), если
в результате подстановки этих чисел вместо 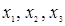 все три уравнения системы обращаются в тождества.

Систему (28) можно переписать в матричном виде:

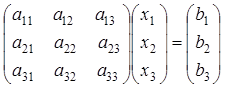, или AX = B,

где A – это матрица коэффициентов при неизвестных, Х – столбец неизвестных, В – столбец свободных членов:

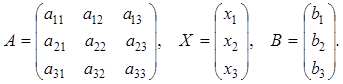
Составим определитель матрицы А и три вспомогательных определителя:

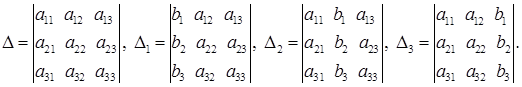(29)

Определитель Δ называется главным определителем системы (28). Вспомогательные определители Δ₁, Δ₂ и Δ₃ получаются из Δ заменой элементов соответственно первого, второго и третьего столбцов столбцом свободных членов.

Если определитель 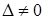, то существует единственное решение системы (28) и оно выражается формулами:

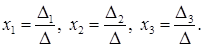                             (30)

Формулы (30) называются формулами Крамера.

5. Решение системы трех линейных алгебраических уравнений
при помощи обратной матрицы

Присоединенной (союзной) матрицей к квадратной матрице

А = 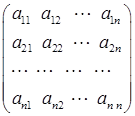 называется матрица

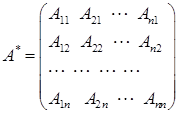,                                          (31)

где 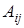 – алгебраические дополнения элементов  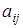определителя матрицы А.

Матрица 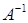 называется обратной к квадратной матрице А, если выполнено условие: 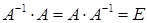, где Е – единичная матрица той же размерности, что и А.

Обратная матрица существует тогда и только тогда, когда квадратная матрица А – невырожденная, т. е. .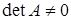

Чтобы найти обратную матрицу 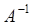, необходимо:

а) проверить невырожденность матрицы А, вычислив определитель detA;

б) найти союзную матрицу А^* к матрице А;

в) найти обратную матрицу по формуле:

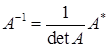.                                          (32)

Если систему линейных алгебраических уравнений (28) переписать
в матричном виде AX = B, то ее решение можно получить матричным способом, т. е. при помощи обратной матрицы:

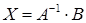,                                            (33)

где 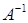– обратная матрица для данной матрицы А.