Содержание
[развернуть]
Тригонометрические функции в прямоугольном треугольнике 
Править
Чтобы определить тригонометрические функции произвольного угла α, возьмём произвольный прямоугольный треугольник, содержащий угол α. Стороны этого треугольника мы будем называть так:
§ Гипотенуза — сторона, противолежащая прямому углу, самая длинная сторона в треугольнике. В данном случае, сторона c.
§ Противолежащий катет — катет, лежащий напротив угла. Например, катет a — противолежащий по отношению к углу A.
§ Прилежащий катет — катет, являющийся стороной угла. Например, катет b — прилежащий по отношению к углу A.
Будем предполагать, что треугольник лежит в евклидовой плоскости, поэтому сумма его углов равна π.Это означает, что углы между катетами и гипотенузой лежат между 0 и π2. Используя формулы приведения или определение через единичную окружность, можно расширить область определения тригонометрических функций на множество вещественных чисел.
Си́нус угла — отношение противолежащего катета к гипотенузе: sinα=ac. Это отношение не зависит от выбора треугольника ABC, содержащего угол α, так как все такие треугольники подобны.
Ко́синус угла — отношение прилежащего катета к гипотенузе: cosα=bc. Так как sinβ=bc, синус одного острого угла в треугольнике равна косинусу второго, и наоборот.
Та́нгенс угла — отношение противолежащего катета к прилежащему: tgα=ab.
Кота́нгенс угла — отношение прилежащего катета к противолежащему: ctgα=ba. Котангенс одного острого угла в прямоугольном треугольнике равен тангенсу второго, и наоборот.
Се́канс угла — отношение гипотенузы к прилежащему катету: secα=cb.
Косе́канс угла — отношение гипотенузы к противолежащему катету: cosecα=ca.
Из определений тригонометрических функций следует:
a=csinα,
b=ccosα,
a=btgα,
b=actgα,
c=bsecα,
c=acosecα,
и симметрично:
b=csinβ,
a=ccosβ,
b=atgβ,
a=bctgβ,
c=asecβ,
c=bcosecβ.
Определение тригонометрических функций через окружность Править
Пусть на плоскости задана прямоугольная система координат с началом в точке O и с осями OX и OY . Возьмём в этой системе координат окружность с центром в точке O и радиусом, равным единице. Пусть отрезок OA поворачивается на произвольный угол ϑ вокруг центра O.
Синусом угла ϑ называется отношение ординаты точки A к длине отрезка OA. Обозначают sinϑ=ACOA.Так как длина отрезка OA равна 1, то sinϑ=AC.
Косинусом угла ϑ называется отношение абсциссы точки A к длине отрезка OA. Обозначают cosϑ=OCOA. Так как длина отрезка OA равна 1, то cosϑ=OC.
Тангенсом угла ϑ называется отношение ординаты точки A к абсциссе точки A. Обозначают tgϑ=ACOC(в англоязычной литературе tanϑ). Так как AC=sinϑ и OC=cosϑ, то tgϑ=sinϑcosϑ.
Котангенсом угла ϑ называется отношение абсциссы точки A к ординате точки A. Обозначают ctgϑ=OCAC (в англоязычной литературе cotϑ). Так как AC=sinϑ и OC=cosϑ, то ctgϑ=cosϑsinϑ.Котангенс равен обратному значению тангенса: ctgϑ=1tgϑ.
Секансом угла ϑ называется отношение длины отрезка OA к абсциссе точки A. Обозначают secϑ=OAOC.Так как длина отрезка OA равна 1, то secϑ=1OC. Секанс равен обратному значению косинуса: secϑ=1cosϑ.
Косекансом угла ϑ называется отношение длины отрезка OA к ординате точки A. Обозначают cosecϑ=OAAC (в англоязычной литературе cscϑ). Так как длина отрезка OA равна 1, то cosecϑ=1AC.Косеканс равен обратному значению синуса: cosecϑ=1sinϑ.
Из определения следует: если косинус угла равен нулю, то тангенс и секанс этого угла не существуют. Аналогично для котангенса и косеканса: если синус угла равен нулю, то котангенс и косеканс этого угла не существуют.
Определение тригонометрических функций через ряды Править
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенных рядов:
sinx=x−x33!+x55!−x77!+x99!+⋯=∑∞n=0(−1)n x2n+1(2n+1)!,
cosx=1−x22+x44!−x66!+x88!+⋯=∑∞n=0(−1)n x2n(2n)!.
Пользуясь этими формулами, а также уравнениями tgx=sinxcosx, ctgx=cosxsinx, secx=1cosx и cosecx=1sinx, можно найти разложения в ряд Тейлора и других тригонометрических функций:
tgx=x+x33+2x515+17x7315+62x92835+⋯=∑∞n=1(−1)n−122n(22n−1)B2n(2n)!x2n−1(−π2<x<π2),где B n — числа Бернулли.
secx=1+x22+5x424+61x6720+277x88064+⋯=∑∞n=0(−1)n E2n(2n)!x2n, где E n — числа Эйлера.
Значения тригонометрических функций для некоторых углов Править
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице.
| α | 0°(0 рад) | 30° (π/6) | 45° (π/4) | 60° (π/3) | 90° (π/2) | 180° (π) | 270° (3π/2) |
| sinα | 0 | 12 | 2√2 | 3√2 | 1 | 0 | −1 |
| cosα | 1 | 3√2 | 2√2 | 12 | 0 | −1 | 0 |
| tgα | 0 | 13√ | 1 | 3√ | ∞ | 0 | ∞ |
| ctgα | ∞ | 3√ | 1 | 13√ | 0 | ∞ | 0 |
| secα | 1 | 23√ | 2√ | 2 | ∞ | −1 | ∞ |
| cosecα | ∞ | 2 | 2√ | 23√ | 1 | ∞ | −1 |
Значения тригонометрических функций нестандартных углов Править
sinπ10=sin18∘=5√−14tgπ120=tg1.5∘=8−2(2−3√)(3−5√)√−2(2+3√)(5+5√)√8+2(2−3√)(3−5√)√+2(2+3√)(5+5√)√−−−−−−−−−−−−−−−−−−−−−−−−−⎷
cosπ240=116(2−2+2√−−−−−−√−−−−−−−−−−√(2(2+5√)−−−−−−−−√+3√−15−−√)+2+2√−−−−−−√+2−−−−−−−−−−√(6(5+5√)−−−−−−−−√+5√−1))
cosπ17=182⎛⎝⎜217(17−17−−√)2−−−−−−−−−−−√−17−17−−√2−−−−−−−−√−434+217−−√−−−−−−−−−√+317−−√+17−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−⎷+34−217−−√−−−−−−−−−√+17−−√+15⎞⎠⎟−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−⎷
Свойства тригонометрических функций Править
Функция y = cos x — чётная. Функции: y = sin x, y = tg x, y = ctg x — нечётные, то есть:
sin(−x)=−sinx,
cos(−x)=cosx,
tg(−x)=−tgx,
ctg(−x)=−ctgx.
Для острых углов α<π2 справедливо:
sin(π2−α)=cosα,
cos(π2−α)=sinα,
tg(π2−α)=ctgα,
ctg(π2−α)=tgα.
Для углов 0<α<π справедливо:
sin(π−α)=sinα,
cos(π−α)=−cosα,
tg(π−α)=−tgα,α≠π2.
Рассмотрим треугольник ABO (см. Рис. 1). По теореме Пифагора:
(AB)2+(BO)2=(OA)2,
если OA = 1, то AB = sin α и OB = cos α, то есть
sin2α+cos2α=1.(1)
Если разделить выражение (1) на cos2α, то получим следующее тождество:
1+tg2α=1cos2α.(2)
Если разделить выражение (1) на sin2α, то получим следующее тождество:
1+1tg2α=1sin2α,(3)
или
1+ctg2α=1sin2α.(4)
Производные и интегралы Править
Все тригонометрические функции непрерывно дифференцируемы на всей области определения:
(sinx)′=cosx,
(cosx)′=−sinx,
(tgx)′=1cos2x,
(ctgx)′=−1sin2x.
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
История Править
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
· 6sin(t + 2π*k) = sin(t)
· cos(t + 2π*k) = cos(t)
· sin(t + π) = -sin(t)
· cos(t + π) = -cos(t)
· sin(t + π/2) = cos(t)
· cos(t + π/2) = -sin(t)
· tg(t + π*k) = tg(x)
· ctg(t + π*k) = ctg(x)
формул привидения очень много, давайте составим правило по которому будем определять наши тригонометрические функции при использовании формул привидения:
· Если под знаком тригонометрической функции содержатся числа вида: π + t, π - t, 2π + t и 2π - t, то функция не изменится, то есть, например, синус останется синусом, котангенс останется котангенсом.
· Если под знаком тригонометрической функции содержатся числа вида: π/2 + t, π/2 - t,
3π/2 + t и 3π/2 - t, то функция изменится на родственную, т. е. синус станет косинусом, котангенс станет тангенсом.
· Перед получившийся функцией, надо поставить тот знак, который имела бы преобразуемая функция при условии 0 < t < π/2.
Эти правила применимы и когда аргумент функции задан в градусах!
Так же мы можем составить таблицу преобразований тригонометрических функций:
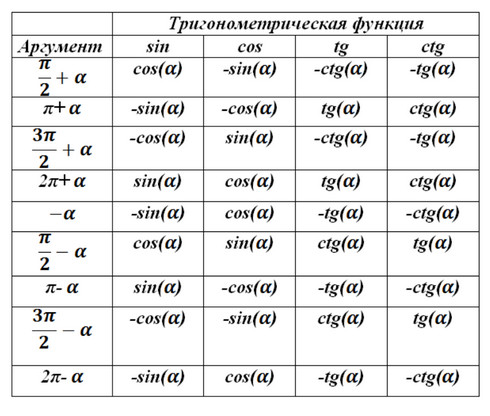
Примеры применения формул приведения
1.Преобразуем cos(π + t). Наименование функции остается, т.е. получим cos(t). Далее предположим, что π/2 < t < π, тогда (π + t) попадет в третью четверть, а там косинус отрицательный, согласно третьему пункту нашего правила, следует поставить минус перед нашей функцией: cos(t + π) = -cos(t)
2. Преобразуем sin(π/2 + t). Наименование функции изменяется, т.е. получим cos(t). Далее предположим что 0 < t < π/2, тогда (π/2 + t) попадет во вторую четверть, а там преобразуемая функция синус положительная, согласно третьему пункту нашего правила, следует поставить положительный знак перед нашей функцией:
sin(t + π/2) = cos(t)
3. Преобразуем tg(π + t). Наименование функции остается, т.е. получим tg(t). Далее предположим, что 0 < t < π/2, тогда (π - t) попадет во вторую четверть, а там тангенс отрицательный, согласно третьему пункту нашего правила следует поставить минус перед нашей функцией: tg(t - π) = -tg(t)
4. Преобразуем ctg(2700 + t). Наименование функции изменяется, то есть получим tg(t). Далее предположим что 0 < t < 900, тогда (2700 + t) попадет в четвертую четверть, а там преобразуемая функция котангенс отрицательная, согласно третьему пункту нашего правила следует поставить минус перед нашей функцией: ctg(2700 + t)=-tg(t).
Задачи с формулами приведения для самостоятельного решения
Ребята, преобразуйте самостоятельно, используя наши правила:
1) tg(π + t),
2) tg(2π - t),
3) ctg(π - t),
4) tg(π/2 - t),
5) ctg(3π + t),
6) sin(2π + t),
7) sin(π/2 + 5t),
8) sin(π/2 - t),
9) sin(2π - t),
10) cos(2π - t),
11) cos(3π/2 + 8t),
12) cos(3π/2 - t),
13) cos(π - t).
8Название модуля: преобразование графиков тригонометрических функций.
Интегрирующая дидактическая цель: отработать навыки построения графиков тригонометрических функций.
Целевой план действий для учащихся:
· повторить основные свойства тригонометрических функций;
· отработать навык преобразования графиков тригонометрических функций;
· способствовать развитию логического мышления;
· воспитывать интерес к изучению предмета.
Банк информации.
Входной контроль.
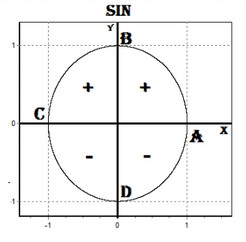
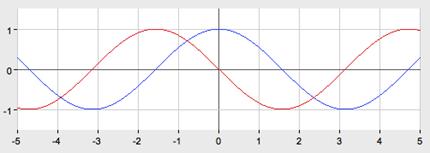
Назовите свойства функций y = sin x (рис. 1).
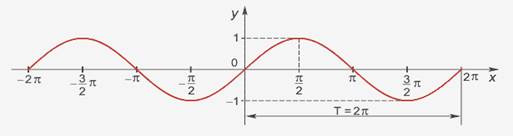
Рис. 1
Свойства:
1. D(y)=R
2. E(y)=[-1;1], функция ограничена
3. sin(-x)=-sinx, функция нечётная
4. Наименьший положительный период: 2π
sin (x+2πn)= sin x, n Є Z, x Є R.
5. sin x=0 при x=πk, kЄ Z
6. sin x>0, x Є (2πk;2π+2πk), k Є Z
7. sin x<0, x Є(π+2πk; 2π+2πk), k Є Z
8. Наибольшее значение, равное 1, y=sin x принимает в точках x=π/2+ 2πk, k Є Z.
9. Наименьшее значение, равное -1, y=sin x принимает в точках x=3π/2+ 2πk, k Є Z.
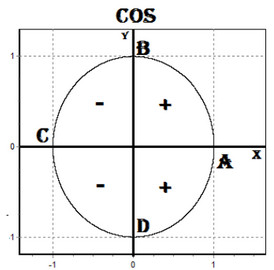
Рассмотрим график фукции y= cos x (рис. 2).
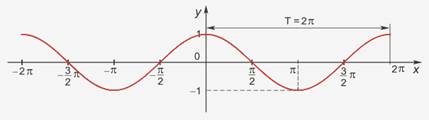
Рис. 2
Свойства:
1. D (y)=R
2. E (y)=[-1;1], функция ограничена
3. cos(-x)= cos x, функция чётная
4. Наименьший положительный период: 2π
cos (x+2πn)=cos x, n Є Z, x Є R
5. cos x=0 при x=π/2+πk, kЄZ
6. cos x>0, x Є (-π/2+2πk; π/2+2πk), k Є Z
7. cos x<0, x Є (π/2+2πk; 3π/2+2πk), k Є Z
8. Наибольшее значение, равное 1, y=cos x принимает в точках x= 2πk, k Є Z.
9. Наименьшее значение, равное -1, y=cos x принимает в точках x=π+ 2πk, k Є Z.
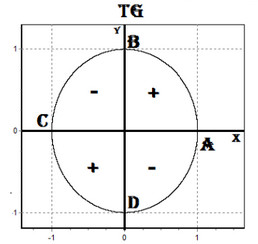
Cледующий график функции y=tg x (рис. 3)
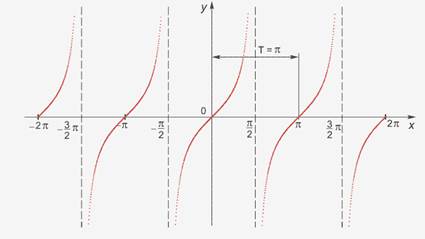
Риc. 3
Свойства:
1. D(y)-множество всех действительных чисел, кроме чисел вида x=π/2 +πk, k Є Z
2. E(y)=(-∞;+ ∞), функция неограниченная
3. tg(-x)=-tg x, функция нечётная
4. наименьший положительный период: π
tg(x+π)= tg x
5. tgx= 0 при x=πk, k Є Z
6. tg x> 0, x Є ( πk; π/2+πk), k Є Z
7. tg x< 0, x Є ( -π/2+πk; πk), k Є z
Следующий график функции y=ctg x (рис. 4)
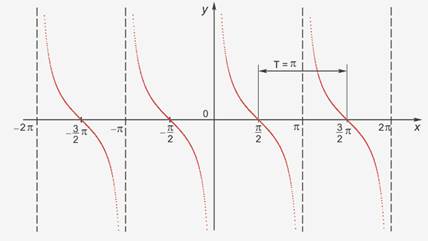
Рис. 4
Свойства:
1. D(y)-множество всех действительных чисел, кроме чисел вида x=πk, k Є Z
2. E(y)= (-∞;+ ∞), функция неограниченная
3. ctg(-x)=-ctg x, функция нечётная
4. Наименьший положительный период: π
ctg(x+π)=tg x
5. ctg x = 0 при x=π/2+πk, k Є Z
6. ctg x>0, x Є( πk; π/2+πk), k Є Z
7. ctg x<0, x Є( - π/2+πk; πk), k Є Z
Объяснение материала.
1. Для построения графика функции y=f(x)+a, где a - постоянное число, надо перенести график y=f(x)вдоль оси ординат. Если a>0, то график переносим параллельно самому себе вверх, если a < 0, то – вниз.
2. Для построения графика функции y=kf(x) надо растянуть график функции y=f(x) в k раз вдоль оси ординат. Если |k|>1, то происходит растяжение графика вдоль оси OY, если 0<|k|<1, то – сжатие.
3. График функции y=f(x+b) получается из графика y=f(x) путем параллельного переноса вдоль оси абсцисс. Если b>0 , то график перемещается влево, если b<0, то – вправо.
4. Для построения графика функции y=f(kx) надо растянуть график y=f(x) вдоль оси абсцисс. Если |k|>1, то происходит сжатие графика вдоль оси OХ, если 0<|k|<1 , то – растяжение.
Закрепление материала.
Уровень А
Частная дидактическая цель: отработать навык построения тригонометрических функций путем преобразований.
Методический комментарий для учащихся: постройте графики функций, выполнив преобразования.
1. 
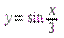
График функции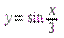 
получается из графика 
путем растяжения вдоль оси Ox в 3 раза.
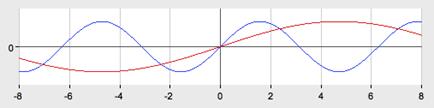
2. 
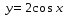
График функции получается из графика 
путем растяжения вдоль оси Oy в 2 раза.
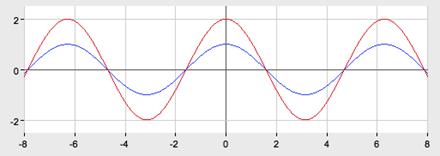
3. 
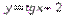
График функции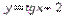 
получается из графика 
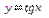путем параллельного переноса на 2 единицы вверх вдоль оси Oy.
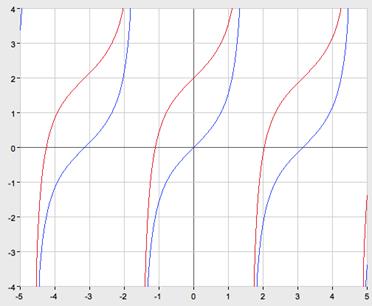
4. 
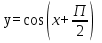
График функции получается из графика 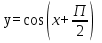путем параллельного переноса вдоль осиабсцисс на 
единиц влево.
5. 
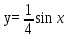
Г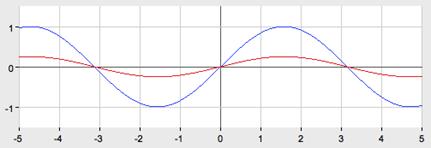 
рафик функции 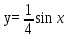получается из графика 
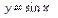путем сжатия вдоль оси Oy в 4 раза.
Уровень В.
Частная дидактическая цель: отработать навык построения графиков тригонометрических функцийпутем последовательного применения преобразований.
Методический комментарий для учащихся: постройте графики функций, выполнив преобразования.
1. 
График функции получается из графика путем параллельного переноса вдоль осиабсцисс на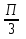 
единиц вправо.
2. 
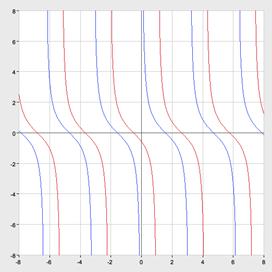
График функции получается из графика функции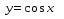 
путем последовательного выполнения следующих преобразований:
1) параллельный перенос на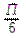 
единицы влево вдоль оси абсцисс
2) сжатие вдоль оси Оy в 4 раза.
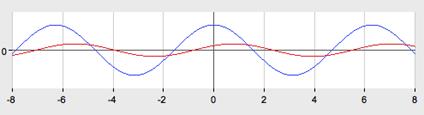
3. 
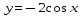
График функции 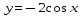получается из графика функции 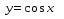, каждая ордината которого изменяется в -2 раза. Для этого выполняем следующие преобразования:
1) отображаем симметрично относительно оси Ox,
2) растягиваем в 2 раза вдоль оси Oy.
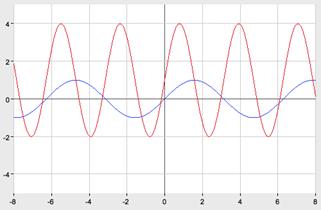
4. 
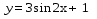
График функции 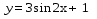получается из графика функции 
последовательноговыполнения следующих преобразований:
1) сжатие вдоль оси абсцисс в 2 раза;
2) растяжение в 3 раза вдоль оси Oy;
3) параллельный перенос на 1 единицу вверх вдоль оси ординат.
Уровень С.
Частная дидактическая цель: отработать навык построения графиков тригонометрических функцийпутем последовательного применения преобразований.
Методический комментарий для учащихся: укажите, какие преобразования нужно выполнить дляпостроения графиков. Постройте графики.
1. 
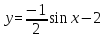
График функции по 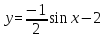лучается из графика функции 
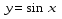путем последовательного выполнения следующих преобразований:
1) отображение симметрично относительно оси Ox,
2) сжатие в 2 раза вдоль оси Oy;
3) параллельный перенос на 2 единицы вниз вдоль оси Оy.
2. 
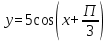
График функции 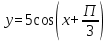получается из графика функции 
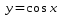последовательноговыполнения следующих преобразований:
1) параллельный перенос вдоль оси абсцисс на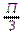 
единиц влево,
2) растяжение в 5 раза вдоль оси Oy.
3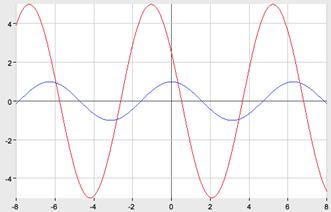 
. 
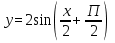
График функции 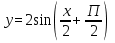получается из графика функции 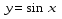последовательноговыполнения следующих преобразований:
1) растяжение вдоль оси абсцисс в 2 раза;
2) параллельный перенос на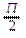 
единиц влево вдоль оси абсцисс.
3) растяжение в 2 раза вдоль оси Oy.
4. 
Так как cos (-x)=cos x, следовательно, y= cos x - чётная функция, значит, график функции тот же, что и график функции y= cos x.
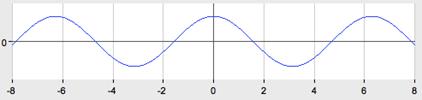
5. 
График функции получается из графика функции .Части графика функции 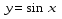, расположенные ниже оси абсцисс, зеркально отразятся и будут распо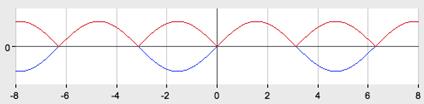 
ложены в верхней полуплоскости.
Дата: 2018-12-28, просмотров: 331.
