7.1. Линейные дифференциальные уравнения 2-го порядка с частными производными
Дифференциальным уравнением 2-го порядка с частными производными относительно неизвестной функции U = U (x, y) называется уравнение вида:
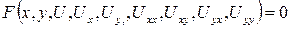 ,
,
где U = U (x, y) – неизвестная функция от x, y, 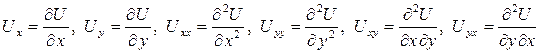 .
.
Линейным дифференциальным уравнением 2-го порядка с частными производными называется уравнение вида:
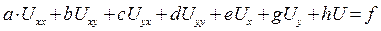 ,
,
где a, b, c, d, e, g, h, f – известные непрерывные функции от x, y (в частности, они могут быть постоянными).
Иногда рассматривается функция U = U (x, t), где t – время.
Дифференциальные уравнения с частными производными, описывающие некоторый физический процесс, называют уравнениями математической физики. Для физических приложений наиболее важными являются три типа таких уравнений:
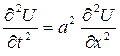 – волновое уравнение;
– волновое уравнение;
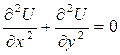 – уравнение Лапласа;
– уравнение Лапласа;
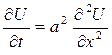 – уравнение теплопроводности.
– уравнение теплопроводности.
Например, рассматривается задача о распределении температуры в однородном стержне, теплоизолированном от внешней среды по боковой поверхности и имеющем длину L.
Обозначив через х – абсциссу сечения стержня (х 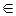 [0; L]), t – время, U = U (x, t) – температуру в сечении стержня с абсциссой х в момент времени t, получим модель этой задачи – уравнение теплопроводности. Коэффициент а в этом уравнении зависит от физических свойств материала, из которого изготовлен стержень.
[0; L]), t – время, U = U (x, t) – температуру в сечении стержня с абсциссой х в момент времени t, получим модель этой задачи – уравнение теплопроводности. Коэффициент а в этом уравнении зависит от физических свойств материала, из которого изготовлен стержень.
Для описания реального физического процесса кроме дифференциальных уравнений необходимо задать еще начальное состояние процесса – начальные условия, а также значения неизвестной функции или ее производных на границе рассматриваемой области – граничные (краевые) условия.
Начальные условия задают, как правило, при t = 0.
Краевые условия задают на границе области, например, для уравнения теплопроводности задают значения функции U (x, t) при х = 0; х = L в любой момент времени t 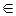 [0; T].
[0; T].
Если заданы и начальные, и краевые условия, то говорят о смешанной задаче для дифференциального уравнения с частными производными.
7.2. Решение уравнения теплопроводности методом сеток
Пусть требуется решить смешанную задачу для уравнения теплопроводности, т.е. найти функцию U (x, t), удовлетворяющую дифференциальному уравнению с частными производными
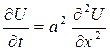 , (18)
, (18)
где U = U (x, t) – температура в сечении стержня с абсциссой х в момент времени t, если известны:
температура в сечении стержня с абсциссой х в момент времени t = 0:
U (х, 0) = f (x) для 0 £ x £ L, (19)
и температура на концах стержня в любой момент времени t:
U (0, t) = α (t), U (L, t) = β (t) для 0 £ t £ T, (20)
где f (x), α (t), β (t) – известные непрерывные функции.
Будем предполагать, что смешанная задача (18)-(20) имеет единственное решение U = U (x, t) в области 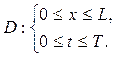
Используем конечно-разностный метод приближенного решения задачи, называемый также методом сеток.
Введем прямоугольную сетку, построенную на области D:
xi = ih для i = 0, 1, 2,….,n,
tk = kd для k = 0,1, 2,….,m,
где h = 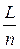 – шаг сетки по х, d =
– шаг сетки по х, d = 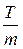 – шаг сетки по t. При этом прямоугольная область D будет разбита на прямоугольные части прямыми х = xi и t = tk в системе координат Ох t . Точки (xi, tk), лежащие на пересечении этих прямых, называют узлами двумерной сетки, или просто узлами.
– шаг сетки по t. При этом прямоугольная область D будет разбита на прямоугольные части прямыми х = xi и t = tk в системе координат Ох t . Точки (xi, tk), лежащие на пересечении этих прямых, называют узлами двумерной сетки, или просто узлами.
Вместо неизвестной функции U (x, t) будем рассматривать функцию, заданную в узлах сетки: ui, k = u(i, k), которую называют сеточной функцией. Будем искать значения сеточной функции, соответствующие приближенному решению задачи, т.е. ui, k » U (xi, tk).
Неизвестные u0, k и un, k для k = 0, 1,….,m находят из граничных условий (20):
u0, k = U (0, tk) = α (tk), un, k = U (L, tk) = β (tk).
Значения ui ,0, соответствующие моменту времени t0 = 0, находят из начальных условий (19):
ui, 0 = U (xi, 0) = f (xi), для i= 1,….,n –1.
Для определения значений ui, k во внутренних узлах заменим частные производные отношениями конечных разностей по приближенным формулам:
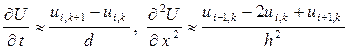 ,
,
тогда уравнению (18) будет соответствовать сеточное уравнение:
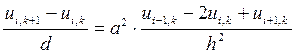 .
.
Если выбрать 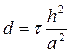 , то получим простую формулу для вычисления значений сеточной функции:
, то получим простую формулу для вычисления значений сеточной функции: 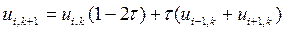 .
.
Можно доказать, что для значений 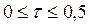 получается устойчивое решение смешанной задачи, т.е. малым изменениям исходных данных задачи будут соответствовать лишь малые изменения полученного решения.
получается устойчивое решение смешанной задачи, т.е. малым изменениям исходных данных задачи будут соответствовать лишь малые изменения полученного решения.
Если выбрать шаги сетки h и d таким образом, чтобы было выполнено условие 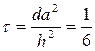 , то получается наиболее точная формула для расчетов:
, то получается наиболее точная формула для расчетов:
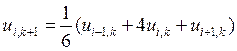 ,
,
для i = 1, 2,….,n – 1, k = 0, 1,….,m – 1.
Значения ui , k для i = 1, 2,….,n – 1 находят «по слоям»: сначала вычисляют ui 0 на «нулевом слое», затем вычисляют ui ,1, ui ,2 ,… – значения на каждом следующем, «(k +1)-м слое», соответствующем моменту времени tk+1, используя значения на предыдущем, «k-м слое».
Окончательно получаем разностную модель задачи – расчетные формулы для вычисления всех значений функции U (xi, tk) = ui, k в узлах сетки, покрывающей область D:
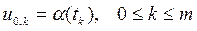 , (21)
, (21)
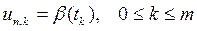 , (22)
, (22)
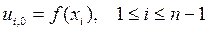 , (23)
, (23)
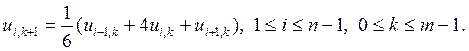 (24)
(24)
Решение примерного варианта контрольной работы
Задача 1. Даны приближенные значения величин x = 1,6, y = 0,35, где D(х) = 0,02, d (y) = 4%. Требуется:
1) вычислить значение величины 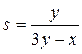 , оценить предельную абсолютную погрешность D(s) и округлить значение s в соответствии с погрешностью;
, оценить предельную абсолютную погрешность D(s) и округлить значение s в соответствии с погрешностью;
2) вычислить приближенное значение функции f (x, y) = 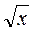 ·(2x – 3y), оценить предельную абсолютную погрешность значения функции и округлить его в соответствии с погрешностью.
·(2x – 3y), оценить предельную абсолютную погрешность значения функции и округлить его в соответствии с погрешностью.
Решение.
1). Вычислим приближенное значение s: s = 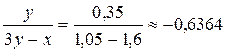 .
.
Оценим предельную абсолютную погрешность результата по формуле (2), в которой
D(х) = 0,02; D(y) = y · d (y) = 0,35·0,04 = 0,014,
следовательно, по формуле (1) получаем:
D(3y – х) = 3D(y) + D(х) = 0,062.
Предельная абсолютная погрешность значения s:
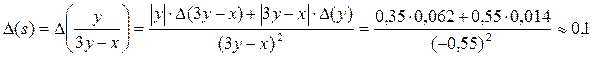 .
.
Округлим значение s, оставляя столько же цифр после запятой, сколько их в записи абсолютной погрешности результата: D(s) = 0,1, следовательно, значение s округляем до одного знака после запятой: s » – 0,6.
2). Вычислим приближенное значение функции f (x, y) = 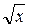 ·(2x – 3y):
·(2x – 3y):
f (1,6; 0,35) = 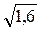 ·(3,2 – 1,05) » 1,2649·2,15 » 2,7196.
·(3,2 – 1,05) » 1,2649·2,15 » 2,7196.
Оценим предельную абсолютную погрешность результата по формуле (4), в которой:
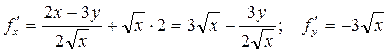 ;
;
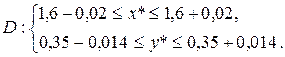
Максимальные значения модулей частных производных:
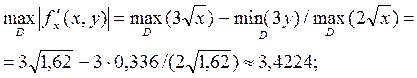
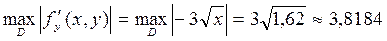 .
.
Предельная абсолютная погрешность значения функции:
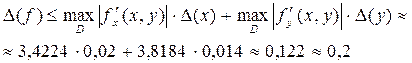
(округление абсолютной погрешности производится «с избытком»).
Округлим значение функции, оставляя столько же цифр после запятой, сколько их в записи абсолютной погрешности результата: D(f) = 0,2, тогда f (1,6; 0,35) » 2,7.
Ответы: 1) s » – 0,6; D(s) = 0,1;
2) f (1,6; 0,35) » 2,7; D(f) = 0,2.
Задача 2. Дано уравнение: x5 + 3x – 2,5 = 0. Требуется:
1) определить число корней уравнения и найти промежутки их изоляции;
2) вычислить значение одного из корней уравнения с точностью ε = 0,01 при помощи метода деления отрезка пополам.
Решение.
1). Будем искать такой интервал (a, b), в котором содержится корень уравнения x5 + 3x – 2,5 = 0, причем только один. Для этого найдем производную 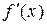 = 5х4 + 3. Из того, что
= 5х4 + 3. Из того, что 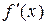 > 0 для любых значений x, следует, что функция f (x) = x5 + 3x – 2,5 монотонно возрастающая, значит, уравнение f (x) = 0 имеет только один корень (точку пересечения графика y = f (x) с осью абсцисс).
> 0 для любых значений x, следует, что функция f (x) = x5 + 3x – 2,5 монотонно возрастающая, значит, уравнение f (x) = 0 имеет только один корень (точку пересечения графика y = f (x) с осью абсцисс).
Подбором находим две точки, в которых функция имеет разные знаки: например, точки a = 0,5, b = 1 (чем ближе друг к другу эти точки, тем меньше потребуется сделать вычислений на этапе уточнения корня). Проверка: 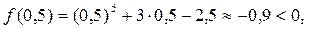
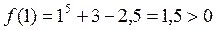 , следовательно,
, следовательно, 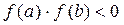 и корень уравнения
и корень уравнения 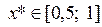 .
.
2). Уточним корень уравнения x5 + 3x – 2,5 = 0 с точностью ε = 0,01 методом деления отрезка пополам.
Для этого обозначим: номер шага k = 0; a0 = a = 0,5; b0 = b = 1, и вычислим начальное значение корня 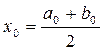 = 0,75 и значение функции f (x0) =
= 0,75 и значение функции f (x0) = 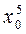 + 3x0–2,5 » – 0,0127 (все промежуточные вычисления будем производить, используя 4 десятичных знака после запятой).
+ 3x0–2,5 » – 0,0127 (все промежуточные вычисления будем производить, используя 4 десятичных знака после запятой).
Для k = 1 находим ak, bk. По формулам (8.1) –(8.2). Поскольку f (x0) < 0, то выполнены условия 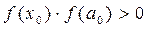 ,
, 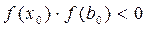 , поэтому a1:= x0 и b1:= b0, т.е. [a1;b1] = [0,75; 1]. После этого вычислим
, поэтому a1:= x0 и b1:= b0, т.е. [a1;b1] = [0,75; 1]. После этого вычислим 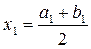 = 0,875, значение функции f (x1) » 0,6379 и проверим выполнение условия (9):
= 0,875, значение функции f (x1) » 0,6379 и проверим выполнение условия (9): 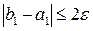 . Получаем:
. Получаем: 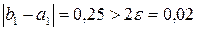 . Условие не выполнено, следовательно, переходим к следующему шагу.
. Условие не выполнено, следовательно, переходим к следующему шагу.
Для k = 2, 3,…. находим ak, bk, xk по формулам (8.1) – (8.3), проверяя на каждом шагу выполнение условия (9): 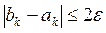 и, если оно выполнено, определяем знак f (xk). Если f (xk) < 0, то на следующем шаге изменяем ak, а если f (xk) > 0, то изменяем bk, чтобы на каждом шаге выполнялось условие
и, если оно выполнено, определяем знак f (xk). Если f (xk) < 0, то на следующем шаге изменяем ak, а если f (xk) > 0, то изменяем bk, чтобы на каждом шаге выполнялось условие 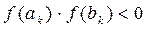 . Результаты расчетов заносим в таблицу:
. Результаты расчетов заносим в таблицу:
| k | ak | bk | 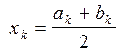
| 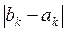
| f (xk) = 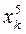 + 3xk–2,5 + 3xk–2,5
|
| 0 | 0,5 | 1 | 0,75 | 0,5 | – 0,0127 < 0 |
| 1 | 0,75 | 1 | 0,875 | 0,25 | 0,6379 > 0 |
| 2 | 0,75 | 0,875 | 0,8125 | 0,125 | 0,2916 > 0 |
| 3 | 0,75 | 0,8125 | 0,7813 | 0,0625 | 0,1348 > 0 |
| 4 | 0,75 | 0,7813 | 0,7656 | 0,0313 | 0,0600 > 0 |
| 5 | 0,75 | 0,7656 | 0,7578 | 0,0156 |
Процесс вычислений закончен, т.к. 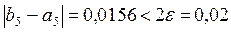 . Последнее значение x5 округляем в соответствии с заданной точностью ε = 0,01:
. Последнее значение x5 округляем в соответствии с заданной точностью ε = 0,01:
х* » x5 » 0,76.
Ответ: 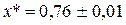 .
.
Задача 3. Дана система линейных алгебраических уравнений:
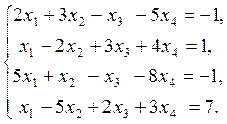
Требуется:
1) решить систему методом Гаусса;
2) вычислить определитель матрицы системы, используя метод Гаусса.
Решение.
1) Решение системы.
Прямой ход. Построим расширенную матрицу (A |В) размерности n 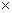 (n + 1), т.е. 5
(n + 1), т.е. 5 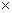 6, присоединив к матрице А столбец свободных членов В:
6, присоединив к матрице А столбец свободных членов В:
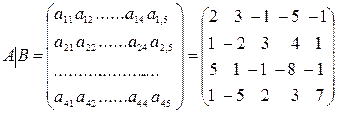
Приведение системы к верхнему треугольному виду осуществляем за 3 шага, используя формулы (10), (11).
1шаг (k = 1): исключаем неизвестную х1 из уравнений с номерами i = 2, 3, 4.
Все элементы 1-й (ведущей) строки расширенной матрицы делим на число d1 = а11 = 2, получаем строку: 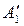 = (1; 1,5; –0,5; –2,5; –0,5).
= (1; 1,5; –0,5; –2,5; –0,5).
Из 2-й строки вычитаем строку 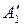 , умноженную на число с21 = а21= 1:
, умноженную на число с21 = а21= 1:
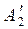 = (1; –2; 3; 4; 1) – (1; 1,5; –0,5; –2,5; –0,5) = (0; –3,5; 3,5; 6,5; 1,5).
= (1; –2; 3; 4; 1) – (1; 1,5; –0,5; –2,5; –0,5) = (0; –3,5; 3,5; 6,5; 1,5).
Из 3-й строки вычитаем строку 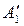 , умноженную на число с31 = а31= 5, получаем:
, умноженную на число с31 = а31= 5, получаем:
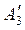 = (5; 1; –1; –8; –1) – 5 (1; 1,5; –0,5; –2,5; –0,5) = (0; –6,5; 1,5; 4,5; 1,5).
= (5; 1; –1; –8; –1) – 5 (1; 1,5; –0,5; –2,5; –0,5) = (0; –6,5; 1,5; 4,5; 1,5).
Из 4-й строки вычитаем строку 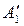 , умноженную на число с41 = а41= 1:
, умноженную на число с41 = а41= 1:
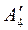 = (1; –5; 2; 3; 7) – (1; 1,5; –0,5; –2,5; –0,5) = (0; –6,5; 2,5; 5,5; 7,5).
= (1; –5; 2; 3; 7) – (1; 1,5; –0,5; –2,5; –0,5) = (0; –6,5; 2,5; 5,5; 7,5).
В результате 1-го шага произошло исключение неизвестной х1 из 2-го, 3-го и 4-го уравнений системы, расширенная матрица и система теперь имеют вид:
(A |В)′ = 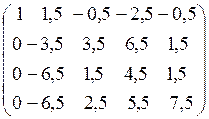 ,
, 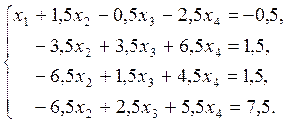
Далее работаем только с 2, 3, 4 строками расширенной матрицы (A | B)′.
2шаг (k = 2): исключаем неизвестную х2 из уравнений с номерами i = 3,4.
Все элементы 2-й (ведущей) строки делим на число d2 = a′22 = –3,5, получаем строку: 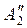 » (0; 1; –1; –1,8571; –0,4286) (все промежуточные вычисления будем производить, округляя результаты до 4 десятичных знаков после запятой).
» (0; 1; –1; –1,8571; –0,4286) (все промежуточные вычисления будем производить, округляя результаты до 4 десятичных знаков после запятой).
Из 3-й строки вычитаем строку 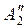 , умноженную на с32 = a′32 = –6,5:
, умноженную на с32 = a′32 = –6,5:
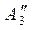 » (0; –6,5; 1,5; 4,5; 1,5) + 6,5 (0; 1; –1; –1,8571; –0,4286) »
» (0; –6,5; 1,5; 4,5; 1,5) + 6,5 (0; 1; –1; –1,8571; –0,4286) »
» (0; 0; –5; –7,5712; –1,2859).
Из 4-й строки вычитаем строку 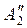 , умноженную на с42 = a′42 = –6,5:
, умноженную на с42 = a′42 = –6,5:
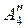 » (0; –6,5; 2,5; 5,5; 7,5) + 6,5 (0; 1; –1; –1,8571; –0,4286) »
» (0; –6,5; 2,5; 5,5; 7,5) + 6,5 (0; 1; –1; –1,8571; –0,4286) »
» (0; 0; –4; –6,5712; 4,7141).
В результате 2-го шага произошло исключение неизвестной х2 из 3-го и 4-го уравнений системы, расширенная матрица и система теперь имеют вид:
(A |В)′′= 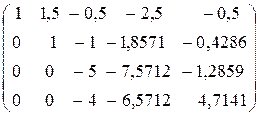 ,
, 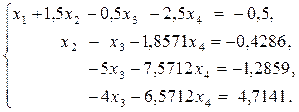
Далее работаем только с 3, 4 строками расширенной матрицы (A | B)′′.
3шаг (k = 3): исключаем неизвестную х3 из уравнения с номером i = 4.
Все элементы 3-й (ведущей) строки делим на число d3 = a′′33 = –5, получаем строку: 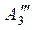 » (0; 0; 1; 1,5142; 0,2572).
» (0; 0; 1; 1,5142; 0,2572).
Из 4-й строки вычитаем строку 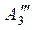 , умноженную на с43 = a′′43 = – 4:
, умноженную на с43 = a′′43 = – 4:
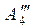 » (0; 0; –4; –6,5712; 4,7141) + 4 (0; 0; 1; 1,5142; 0,2572)»
» (0; 0; –4; –6,5712; 4,7141) + 4 (0; 0; 1; 1,5142; 0,2572)»
» (0; 0; 0; –0,5144; 5,7429).
В результате 3-го шага произошло исключение неизвестной х3 из 4-го уравнения системы, расширенная матрица теперь имеет вид:
(A |В)′′′= 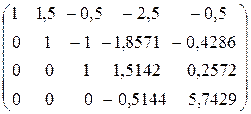 ,
,
Таким образом, в результате прямого хода получили систему с матрицей верхнего треугольного вида.
Преобразования прямого хода можно записать в следующем кратком виде:
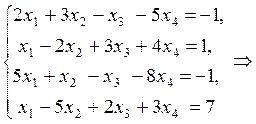
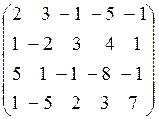 ~
~
~ 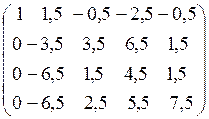 ~
~ 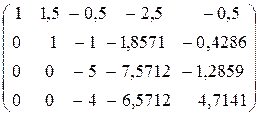 ~
~
~ 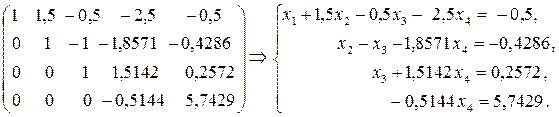

Обратный ход. Находим неизвестные х4, х3, х2, х1 по формулам (12):
из 4-го уравнения находим: х4 = – 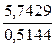 » –11,1643,
» –11,1643,
из 3-го, 2-го и 1-го уравнений последовательно находим:
х3 = 0,2572 – 1,5142 x4 » 17,1622,
х2 = –0,4286 + 1,8571 x4 + x3 » –3,9996,
х1 = –0,5 + 2,5 x4 + 0,5 x3 – 1,5 x2 » –13,8303.
Если округлить значения полученного решения до 2-x десятичных знаков после запятой, получим: х1»–13,83; х2 » –4,00; х3 » 17,16; х4 » –11,16.
2). Для вычисления определителя матрицы системы по формуле (13) перемножаем ведущие элементы всех 3-х шагов на элемент a44′′′ » –0,5144:
det A = a11·a22′·a33′′·a44′′′ = 2 (–3,5) (–5) (–0,5144) = – 18,004 » –18.
Ответы:
1) решение системы: х1» –13,83; х2 » –4,00; х3 » 17,16; х4 » –11,16;
2) определитель матрицы системы det A » –18.
Задача 4. Дана таблица значений функции f (x):
| xi | – 0,5 | – 0,2 | 0,1 | 0,4 | 0,7 |
| f (xi) | 3,2216 | 5,3468 | 4,9472 | 1,5327 | 2,5003 |
Требуется:
1) по табличным данным построить для функции f (x) интерполяционный полином 4-го порядка в форме Лагранжа и привести его к стандартному виду целого многочлена;
2) используя полученный полином, вычислить приближенное значение
функции f (x) в точке 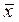 = 0,2.
= 0,2.
Решение.
1). Все значения xi в данной таблице образуют равномерную сетку:
xi = x0 + ih, где x0 = – 0,5, h = 0,3 для i = 0, 1, 2, 3, 4. Построим интерполяционный полином Лагранжа 4-го порядка по формуле (14), подставляя в нее значения xi и yi = f (xi):
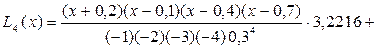
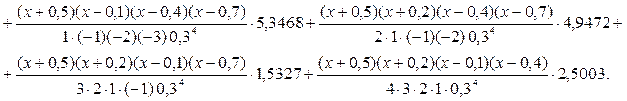
Приведем полученный полином к стандартному виду, произведя упрощения:
L4(x) » 16,572(x4 – x3 + 0,15x2 + 0,05x – 0,0056) – 110,016 (x4 – 0,7x3 – 0,21x2 +
+ 0,167x – 0,014) + 152,691(x4 – 0,4x3 – 0,39x2 + 0,086x + 0,028) – 31,537(x4 –
– 0,1x3 – 0,39x2 – 0,031x + 0,007) + 12,8616 (x4 + 0,2x3 – 0,21x2 – 0,022x +
– + 0,004) = 40,5716x4 + 5,0888x3 – 24,3618x2 – 3,7180x + 5,5535
(промежуточные вычисления производим, используя 4 десятичных знака после запятой).
2). Вычислим значение f ( 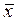 ) с округлением до 3-го знака после запятой:
) с округлением до 3-го знака после запятой:
f ( 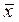 ) = f (0,2) » L4(0,2) »
) = f (0,2) » L4(0,2) »
» 40,5716·0,24 + 5,0888·0,23 – 24,3618·0,22 – 3,7180·0,2 + 5,5535» 3,941.
Ответы:
1) интерполяционный полином в стандартном виде:
L4(x) » 40,5716x4 + 5,0888x3 – 24,3618x2 – 3,7180x + 5,5535;
2) значение f ( 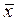 ) = f (0,2) » 3,941.
) = f (0,2) » 3,941.
Задача 5. Дан определенный интеграл 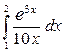 . Составить таблицу значений подынтегральной функции в точках xi = 1 + ih, где i = 0, 1, …,10 с шагом
. Составить таблицу значений подынтегральной функции в точках xi = 1 + ih, где i = 0, 1, …,10 с шагом
h = 0,1 и вычислить приближенное значение интеграла, используя эту таблицу и квадратурную формулу Симпсона.
Решение. Для построения таблицы значений подынтегральной функции 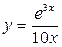 вычисляем значения xi = 1 + ih, где i = 0, 1, …,10, h = 0,1, затем значения функции в этих точках f (xi) = e3x i / (10 xi) и заносим их в таблицу. Для удобства дальнейших вычислений значения функции во внутренних точках xi с нечетными номерами i смещаем влево, а с четными номерами – вправо.
вычисляем значения xi = 1 + ih, где i = 0, 1, …,10, h = 0,1, затем значения функции в этих точках f (xi) = e3x i / (10 xi) и заносим их в таблицу. Для удобства дальнейших вычислений значения функции во внутренних точках xi с нечетными номерами i смещаем влево, а с четными номерами – вправо.
| i | xi = 1 + 0,1i | f (xi) = e3xi / (10 xi) |
| 0 | 1 | 2,0086 |
| 1 | 1,1 | 2,4648 |
| 2 | 1,2 | 3,0499 |
| 3 | 1,3 | 3,8002 |
| 4 | 1,4 | 4,7633 |
| 5 | 1,5 | 6,0011 |
| 6 | 1,6 | 7,5944 |
| 7 | 1,7 | 9,6484 |
| 8 | 1,8 | 12,3004 |
| 9 | 1,9 | 15,7299 |
| 10 | 2 | 20,1714 |
Вычислим определенный интеграл, используя формулу Симпсона. Для этого подставим в формулу (15) 2m = 10, h = 0,1, yi = f (xi) и получим:
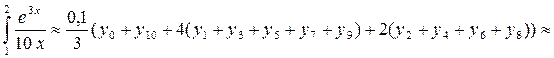
» 0,0333·(2,0086 + 20,1714 + 4 (2,4648 + 3,8002 + 6,0011 + 9,6484 + 15,7299) + + 2·(3,0499 + 4,7633 + 7,5944 + 12,3004)) » 7,606.
Ответ: 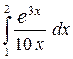 » 7,606.
» 7,606.
Задача 6 . Дана задача Коши для обыкновенного дифференциального уравнения: y′ = 3x – 2y2, y(0) = 0,4. Решить задачу при помощи метода Рунге-Кутты на промежутке [0; 0,5] с шагом h = 0,1.
Решение. Для решения задачи потребуется сделать 5 шагов, т.к.
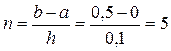 .
.
Результаты промежуточных расчетов по формулам (16) – (17) для i = 0, 1,..,4 будем вносить в рабочую таблицу. Описание расчетов 0-го шага приведем подробно.
Номер шага i = 0, x0 = 0, y(x0) = y0 = 0,4.
Вычислим величины k1, k2, k3, k4:
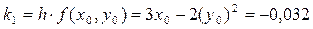 ;
;
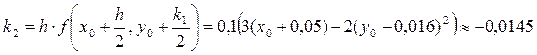 ;
;
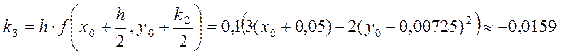 ;
;
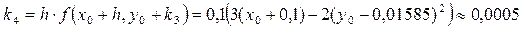 ;
;
следующее значение y1 находим по формуле (17):
y1 = y0 + 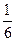 (k1 + 2k2 + 2k3 + k4) » 0,3846.
(k1 + 2k2 + 2k3 + k4) » 0,3846.
Далее фиксируем номер шага i = 1, x1= 0 +ih = 0,1, y(x1) = y1 » 0,3846, вычисляем величины k1, k2, k3, k4 по формулам:
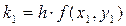 ;
; 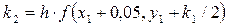 ;
;
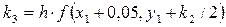 ;
; 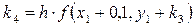
и значение y2.
Затем выполняем все это для i = 2, 3, 4, вычисляя на каждом шагу значения k1, k2, k3, k4 по формулам (17), а следующее значение yi+1 по формуле (16).
Результаты расчетов по шагам оформляем в виде рабочей таблицы:
| i | xi | yi | k1 | k2 | k3 | k4 | yi+1 |
| 0 | 0 | 0,4 | –0,32 | –0,0145 | –0,0159 | 0,0005 | 0,3846 |
| 1 | 0,1 | 0,3846 | 0,0004 | 0,0154 | 0,0142 | 0,0282 | 0,3993 |
| 2 | 0,2 | 0,3993 | 0,0281 | 0,0408 | 0,0398 | 0,0514 | 0,4394 |
| 3 | 0,3 | 0,4394 | 0,0514 | 0,0617 | 0,0608 | 0,0700 | 0,5005 |
| 4 | 0,4 | 0,5005 | 0,0699 | 0,0777 | 0,0768 | 0,0833 | 0,5775 |
В итоге получаем таблицу приближенных значений решения задачи Коши y (x) на промежутке [0; 0,5] с шагом h = 0,1.
Ответ: приближенное решение задачи Коши получено в виде таблицы значений yi » y(xi).
| i | 0 | 1 | 2 | 3 | 4 | 5 |
| xi | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| yi | 0,4 | 0,3846 | 0,3993 | 0,4394 | 0,5005 | 0,5775 |
Задача 7 . Температура однородного стержня U = U (х, t) в сечении х в момент времени t удовлетворяет уравнению теплопроводности. Используя метод сеток, найти решение смешанной задачи для уравнения теплопроводности 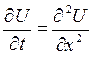 в области
в области 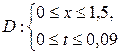 при заданных условиях:
при заданных условиях:
начальное распределение температуры в стержне U (х, 0) = cosx;
температура на концах стержня U (0; t) = 2 t + 1, U (1,5; t) = cos (1,5).
Решение. Для решения используем сетку с шагом h = 0,3 по переменной х и с шагом d = 0,015 по переменной t. Введем следующие обозначения.
Узлы сетки: xi = ih для i = 0, 1, 2, 3, 4, 5, xi 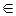 [0; 1,5];
[0; 1,5];
tk = kd для k = 0,1, 2, 3, 4, 5, 6, tk 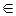 [0; 0,09].
[0; 0,09].
Сеточная функция: ui, k = u(i, k) для i = 0, …5, k = 0, …6, соответствующая приближенному решению задачи, т.е. ui, k » U (xi, tk).
В данном случае шаг d = 0,015 удовлетворяет условию d = h2/6 = 0,09/6, поэтому расчетные формулы для вычисления всех значений функции U (xi, tk) = ui, k в узлах сетки, покрывающей область D, будем получать по формулам (21) – (24).
Результаты вычислений будем заносить в таблицу, построенную в соответствии с заданной сеткой, и имеющей вид:
| i | 0 | 1 | 2 | …… | 5 | |
| k |  xi
tk xi
tk
| 0 | 0,3 | 0,6 | …… | 1,5 |
| 0 | 0 | u0,0 | u1,0 | u2,0 | …… | u5,0 |
| 1 | 0,015 | u0,1 | u1,1 | u2,1 | …… | u5,1 |
| …… | …… | …… | …… | …… | …… | …… |
| 6 | 0,09 | u0,6 | u1,6 | u2,6 | …… | u5,6 |
В этой таблице нужно заполнить затененные ячейки значениями ui, k.
Порядок заполнения таблицы следующий.
1. Заполняем 0-й столбец (температура на левом конце стержня в момент времени tk): u0, k = 2 tk + 1, для k = 0,1, 2, 3, 4, 5, 6.
2. Заполняем последний столбец (температура на правом конце стержня в момент времени tk): u5, k = cos (1,5) для k = 0,1, 2, 3, 4, 5, 6.
3. Заполняем внутренние ячейки 0-й строки (начальная температура в точках с абсциссой xi): вычисляем ui, 0 = cos (xi) для i = 1, 2, 3, 4.
4. Вычисляем значения ui, k во внутренних узлах сетки:
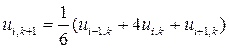 для i = 1, 2, 3, 4, k = 0, 1, 2, 3, 4, 5.
для i = 1, 2, 3, 4, k = 0, 1, 2, 3, 4, 5.
Вычисления производятся по строкам, значения ui-1, k , ui, k и ui+1, k берутся из предыдущей строки. Например, 1-я строка (k + 1 = 1):
u1, 1 = (u0, 0 + 4·u1, 0 + u2, 0)/6 = (1 + 4·0,9553 + 0,8253)/6 » 0,9411;
u2, 1 = (u1, 0 + 4·u2, 0 + u3, 0)/6 = (0,9553 + 4·0,8253 + 0,6216)/6 » 0,8131;
u3, 1 = (u2, 0 + 4·u3, 0 + u4, 0)/6 = (0,8253 + 4·0,6216 + 0,3624)/6 » 0,6124;
u3, 1 = (u3, 0 + 4·u4, 0 + u5, 0)/6 = (0,6216 + 4·0,3624 + 0,0707)/6 » 0,3570.
После заполнения 1-й строки переходим к заполнению 2-й, затем 3-й и т.д., до 6-й строки.
В результате расчетов получаем таблицу:

| i | 0 | 1 | 2 | 3 | 4 | 5 |
| k | xi tk | 0 | 0,3 | 0,6 | 0,9 | 1,2 | 1,5 |
| 0 | 0 | 1 | 0,9553 | 0,8253 | 0,6216 | 0,3624 | 0,0707 |
| 1 | 0,015 | 1,03 | 0,9411 | 0,8131 | 0,6124 | 0,3570 | 0,0707 |
| 2 | 0,03 | 1,06 | 0,9346 | 0,8009 | 0,6032 | 0,3518 | 0,0707 |
| 3 | 0,045 | 1,09 | 0,9332 | 0,7903 | 0,5943 | 0,3469 | 0,0707 |
| 4 | 0,06 | 1,12 | 0,9355 | 0,7814 | 0,5857 | 0,3421 | 0,0707 |
| 5 | 0,075 | 1,15 | 0,9406 | 0,7745 | 0,5777 | 0,3375 | 0,0707 |
| 6 | 0,09 | 1,18 | 0,9478 | 0,7694 | 0,5705 | 0,3331 | 0,0707 |
Ответ: приближенное решение задачи получено в виде таблицы значений
ui, k » U (xi, tk) в узлах сетки области D.
Рекомендуемая литература
1. Волков Е. А. Численные методы: учебное пособие для вузов / Е. А. Волков. – М.: Наука,1987 248 с.
2. Вержбицкий В. М. Основы численных методов: учебник для вузов / В. М. Вержбицкий. – М.: Высш. шк., 2002.– 840 с.
3. Данко, П. Е. Высшая математика в упражнениях и задачах: учебное пособие для втузов. В 2 ч. Ч.2 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова.– М.: Оникс: Мир и образование, 2005.– 416 с.
4. Воробьева, Г. Н., Данилова, А. Н. Практикум по численным методам / Г. Н. Воробьева, А.Н. Данилова.– М.: Высш. школа, 1979.– 184 с.
5. Мостовская Л.Г. Вычислительная математика: учебно-методическое пособие ч.1 / Л. Г. Мостовская, А.-В.И.Середа, – Мурманск, 2001. – 86 с.
Дата: 2018-12-28, просмотров: 449.