Математика
Часть 6
Задания контрольной работы по теме «Численные методы»
и методические указания к ее выполнению
для студентов 2 курса вечерне-заочного факультета
всех специальностей
Контрольная работа №9
Мурманск
2008 г.
УДК 519.06 (076.5)
ББК 22.193 я 73
3 15
Составитель: Мостовская Любовь Григорьевна, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ
Методические рекомендации рассмотрены и одобрены кафедрой ВМ и ПО ЭВМ 05 декабря 2007 г., протокол № 4
Рецензент: Середа А.-В.И., канд. физ.-мат. наук, заведующий кафедрой ВМ и ПО ЭВМ
ÓМурманский государственный технический университет, 2008
Оглавление
Стр.
Введение. 4
Задания на контрольную работу по теме «Численные методы». 5
Содержание теоретического материала и ссылки на литературу.. 8
Справочный материал к выполнению контрольной работы 9
1. Погрешности вычислений. 9
1.1. Абсолютная и относительная погрешности. 9
1.2. Вычисления с учетом погрешностей. 11
2. Решение нелинейных уравнений. 12
2.1. Изоляция корней. 12
2.2. Уточнение корней уравнения методом деления отрезка пополам. 13
3. Решение систем линейных алгебраических уравнений. 15
3.1. Системы линейных алгебраических уравнений. 15
3.2. Решение систем линейных уравнений методом Гаусса. 16
3.3. Вычисление определителя матрицы с использованием метода Гаусса. 17
4. Интерполяционный многочлен в форме Лагранжа и его использование 18
5. Численное интегрирование функции одной переменной. 20
5.1. Квадратурные формулы.. 20
5.2. Квадратурная формула Симпсона. 20
6. Решение обыкновенных дифференциальных уравнений 1-го порядка методом Рунге-Кутты.. 21
7. Решение дифференциальных уравнений с частными производными. 22
7.1. Линейные дифференциальные уравнения 2-го порядка с частными производными. 22
7.2. Решение уравнения теплопроводности методом сеток. 24
Решение примерного варианта контрольной работы.. 26
Рекомендуемая литература.. 38
Введение
Настоящее пособие предназначено для студентов 2 курса вечерне-заочного факультета, обучающихся по техническим специальностям в МГТУ. В пособии содержатся ссылки на теоретический материал по теме «Численные методы», а также список рекомендуемой литературы и задания к выполнению контрольной работы. В результате изучения темы «Численные методы» студенты должны:
• знать основные правила вычисления приближенных значений величин;
• уметь оценивать погрешность полученного результата;
• знать основные методы решения нелинейных уравнений;
• уметь решать системы линейных алгебраических уравнений;
• знать основы интерполирования функций, заданных таблично;
• иметь представление об основных методах численного интегрирования и уметь использовать квадратурные формулы на практике;
• знать численные методы решения обыкновенных дифференциальных уравнений и иметь навыки их использования;
• иметь представление о численных методах решения дифференциальных уравнений с частными производными (уравнений математической физики).
Данные методические рекомендации включают справочный материал, необходимый для выполнения контрольной работы по теме «Численные методы», и решение примерного варианта работы, в котором имеются ссылки на используемый справочный материал.
Задания на контрольную работу по теме «Численные методы»
Контрольная работа состоит из семи задач. Задание для каждой задачи включает в себя ее формулировку и десять вариантов исходных данных.
Перед выполнением контрольной работы необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии со ссылками на литературу, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы.
Задача 1. Даны приближенные значения величин x и y и известно, что абсолютная погрешность D(х) = N /50, а относительная погрешность d (у) = N% (здесь и далее N – номер варианта). Требуется:
1) вычислить значение величины 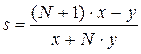 , оценить предельную абсолютную погрешность D(s) и округлить значение s в соответствии с погрешностью;
, оценить предельную абсолютную погрешность D(s) и округлить значение s в соответствии с погрешностью;
2) вычислить приближенное значение функции f (x, y) = ln(x + N)∙(N + y2),
оценить предельную абсолютную погрешность значения функции и округлить его в соответствии с погрешностью.
| Номер варианта | Значения величин x и y | Номер варианта | Значения величин x и y |
| 1 | x = 3,5; y = 0,48 | 2 | x = 4,1; y = 0,29 |
| 3 | x = 2,6; y = 0,54 | 4 | x = 1,4; y = 0,75 |
| 5 | x = 1,7; y = 0,42 | 6 | x = 6,5; y = 0,22 |
| 7 | x = 5,2; y = 0,35 | 8 | x = 3,8; y = 0,72 |
| 9 | x = 2,3; y = 0,62 | 10 | x = 5,9; y = 0,36 |
Задача 2. Дано уравнение N · x3 + x – N/3 = 0 (N – номер варианта). Требуется:
1) определить число корней уравнения и найти промежутки их изоляции;
2) вычислить значение одного из корней уравнения с точностью ε = 0,01 при помощи метода деления отрезка пополам.
Указание. Все промежуточные вычисления производить, используя не менее 4-х десятичных знаков после запятой.
Задача 3. Дана система линейных алгебраических уравнений:
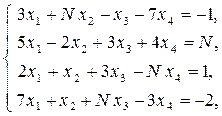 где N – номер варианта.
где N – номер варианта.
Требуется:
1) решить систему методом Гаусса;
2) вычислить определитель матрицы системы, используя метод Гаусса.
Указания. При решении системы использовать расширенную матрицу. Все промежуточные вычисления производить, используя не менее 4-х десятичных знаков после запятой. Округлить значения полученного решения x1, x2, x3, x4 до 2-x десятичных знаков после запятой.
Задача 4. Дана таблица значений функции f (x):
| xi | N – 0,7 | N – 0,3 | N + 0,1 | N + 0,5 | N + 0,9 |
| f (xi) | N/3 | N/6 | N/7 | N/5 | N/2 |
(N – номер варианта).
Требуется:
1) по табличным данным построить для функции f (x) интерполяционный полином 4-го порядка в форме Лагранжа и привести его к стандартному виду целого многочлена;
2) используя полученный полином, вычислить приближенное значение функции f (x) в точке 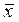 = N + 0,3.
= N + 0,3.
Указания Все вычисления производить, используя не менее 4-х десятичных знаков после запятой. Округлить полученное значение f ( 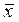 ) до 3-x десятичных знаков после запятой
) до 3-x десятичных знаков после запятой
Задача 5. Дан определенный интеграл 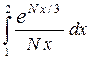 , где N – номер варианта. Требуется: составить таблицу значений подынтегральной функции в точках
, где N – номер варианта. Требуется: составить таблицу значений подынтегральной функции в точках
xi = 1 + ih, где i = 0, 1, …,10 с шагом h = 0,1 и вычислить приближенное значение интеграла, используя эту таблицу и формулу Симпсона.
Указание. Все вычисления производить, используя не менее 4-х десятичных знаков после запятой, полученный результат округлить до 3-х десятичных знаков после запятой.
Задача 6 . Дана задача Коши для обыкновенного дифференциального уравнения: y′ = Nx – y2, y(0) = N/10 (N – номер варианта). Решить задачу при помощи метода Рунге-Кутты на промежутке [0; 0,5] с шагом h = 0,1.
Указание. Все вычисления производить, используя не менее 4-х десятичных знаков после запятой.
Задача 7 . Температура однородного стержня U = U (х, t) в сечении х в момент времени t удовлетворяет уравнению теплопроводности. Используя метод сеток, найти решение смешанной задачи для уравнения теплопроводности 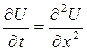 в области
в области 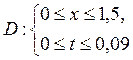 при заданных условиях: начальное распределение температуры в стержне U (х, 0) = f (x), температура на концах стержня U (0; t) = α (t), U (1,5; t) = β (t), где f (x), α (t), β (t) – заданные функции.
при заданных условиях: начальное распределение температуры в стержне U (х, 0) = f (x), температура на концах стержня U (0; t) = α (t), U (1,5; t) = β (t), где f (x), α (t), β (t) – заданные функции.
Указания. Для решения использовать сетку с шагом h = 0,3 по переменной х и с шагом d = 0,015 по переменной t. Все значения функции в узлах сетки вычислять с округлением до 4-го знака после запятой.
| Номер варианта | Функция f (x) | Функция α (t) | Функция β (t) |
| 1 | f (x) = 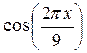
| α (t) = 1 – t2 | β (t) = 0,5 |
| 2 | f (x) = sin х | α (t) = 2 t | β (t) = cos 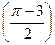
|
| 3 | f (x) = ln (х + 1) | α (t) = t2 | β (t) = ln (2,5) |
| 4 | f (x) = 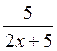
| α (t) = cos t | β (t) = 0,625 |
| 5 | f (x) = x2 + 2х | α (t) = sin t | β (t) = 5,25 |
| 6 | f (x) = 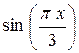
| α (t) = t2 + t | β (t) = 1 |
| 7 | f (x) = 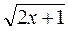
| α (t) = t2 + 1 | β (t) = 2 |
| 8 | f (x) = ln (4 – 2х) | α (t) = ln (t + 4) | β (t) = 0 |
| 9 | f (x) = 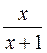
| α (t) = 3 t | β (t) = 0,6 |
| 10 | f (x) = 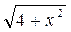
| α (t) = 2cos t | β (t) = 2,5 |
Содержание теоретического материала и ссылки на литературу
| № задачи | Содержание (темы) | Литература |
| 1 | Погрешности вычислений. Предельная абсолютная погрешность и предельная относительная погрешности вычислений. Вычисление приближенных значений функции | [1], гл. 1, §1; [2], гл. 1.1; [4], гл. I, работа №1(1), 2(2); [5], §1, 2.1, 2.2.1 |
| 2 | Методы решения нелинейных уравнений. Метод деления отрезка пополам | [1], гл. 4, §26; [2], гл.5.1, 5.2; [3], гл.IX, № 1168, 1169, 1170, 1178, 1179; [4], гл. IV, работа №1(15); [5], §2 |
| 3 | Численные методы решения систем линейных алгебраических уравнений. Метод Гаусса. Вычисление определителя с использованием метода Гаусса | [1], гл.3, §19; [2], гл. 2.1, 2.2; [4], гл. III, работа №2(7), 3(8); [5], §4.1.1, 6.1, |
| 4 | Полиномиальная интерполяция функций. Интерполяционный полином в форме Лагранжа и его использование | [1], гл. 1, §4, 5; [2], гл. 8.1, 8.2; [3], гл.IX, № 1192-1196; [4], гл. VI, работа №1(32) |
| 5 | Квадратурные формулы численного интегрирования. Формула Симпсона | [1], гл. 2, §15; [2], гл. 12.1, 12.3; [3], гл.IX, № 1205-1207; [4], гл. VII, работа №2(39) |
| 6 | Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений. Метод Рунге - Кутты | [1], гл. 2, §18; [2], гл. 14.1, 14.5, 14.6; [3], гл.IX, № 1234-1237; [4], гл. VIII, работа №2(43) |
| 7 | Понятие о методе сеток. Использование метода сеток для решения уравнений математической физики | [1], гл. 6, §31; [2], гл. 17.3, 19.1, 19.2, 20.1, 20.2; [4], гл. IX, работа №2(48) |
Примечание. Ссылки на литературу в таблице даны в соответствии с номерами в списке рекомендуемой литературы.
Справочный материал к выполнению контрольной работы
Погрешности вычислений
1.1. Абсолютная и относительная погрешности
Практические вычисления проводятся над числами, которые могут быть заданы не только точно, но и приближенно. Например, число 1/3 можно записать в виде десятичной дроби только приближенно.
Правило округления чисел: если первая из отбрасываемых цифр меньше пяти, то все сохраняемые цифры не изменяются, а если первая отбрасываемая цифра больше или равна пяти, то последняя сохраняемая цифра увеличивается на единицу.
Примеры. 13523 » 13500 = 135·102, 2,1564 » 2,16, – 0,325 » –0,33.
Обозначим 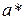 – точное значение некоторой величины, a – приближенное значение этой величины (приближенное число).
– точное значение некоторой величины, a – приближенное значение этой величины (приближенное число).
Величину 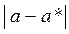 называют абсолютной погрешностью числа a.
называют абсолютной погрешностью числа a.
В большинстве случаев 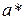 неизвестно, однако, можно указать некоторое число D(a), оценивающее абсолютную погрешность приближенного числа, т.е. удовлетворяющее условию
неизвестно, однако, можно указать некоторое число D(a), оценивающее абсолютную погрешность приближенного числа, т.е. удовлетворяющее условию 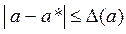 . Число D(a) называют предельной абсолютной погрешностью числа a. Обычно предельную абсолютную погрешность называют просто абсолютной погрешностью и записывают так:
. Число D(a) называют предельной абсолютной погрешностью числа a. Обычно предельную абсолютную погрешность называют просто абсолютной погрешностью и записывают так: 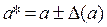 , причем в числах a и D(a) сохраняют одинаковое число знаков после запятой. При округлении предельной абсолютной погрешности его значение всегда берется «с избытком», т.е. последняя сохраняемая цифра увеличивается на единицу.
, причем в числах a и D(a) сохраняют одинаковое число знаков после запятой. При округлении предельной абсолютной погрешности его значение всегда берется «с избытком», т.е. последняя сохраняемая цифра увеличивается на единицу.
Примеры. 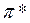 = 3,1416 ± 0,0001;
= 3,1416 ± 0,0001; 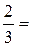 0, 67 ± 0,01.
0, 67 ± 0,01.
Предельной относительной погрешностью числа a называют величину 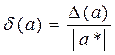 или
или 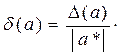 100%. В случае, когда
100%. В случае, когда 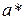 неизвестно, полагают, что d (a) =
неизвестно, полагают, что d (a) = 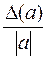 или d (a) =
или d (a) = 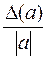 ·100%. Обычно предельную относительную погрешность числа называют просто относительной погрешностью.
·100%. Обычно предельную относительную погрешность числа называют просто относительной погрешностью.
Примеры. 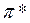 = 3,1416 ± 0,0001
= 3,1416 ± 0,0001 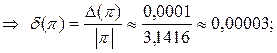
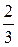 = а* = 0, 67 ± 0,01
= а* = 0, 67 ± 0,01 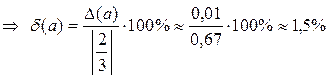 .
.
Первая слева цифра числа, отличная от нуля, и все цифры, расположенные правее нее, называются значащими цифрами числа. В записи погрешностей обычно оставляют одну значащую цифру, например, D(a) = 4·105, D(b) = 0,05, или d (х) = 3%.
Если приближенное число записано без указания его погрешности, то по умолчанию считается, что его абсолютная погрешность не превосходит единицы последнего сохраненного разряда в записи числа, например, запись
а » 2,320 означает, что D(a) = 0,001.
1.2. Вычисления с учетом погрешностей
При выполнении действий над приближенными числами происходит накопление погрешностей, и полученный результат не может быть точнее исходных данных.
Основные формулы для вычисления погрешностей арифметических операций:
D(с*·a) = с*·D(a), если с* – точное число (константа);
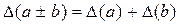 ; (1)
; (1)
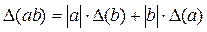 ;
;
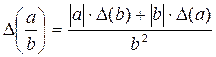 ; (2)
; (2)
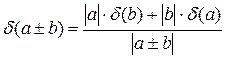 ;
;
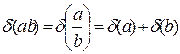 . (3)
. (3)
При выполнении арифметических операций обычно все промежуточные вычисления осуществляют с одной или двумя запасными десятичными цифрами по сравнению с желаемым результатом, а затем полученный результат округляют: либо до требуемой в задаче точности, либо в соответствии абсолютной погрешностью результата (например, если a = 12305362, D(a) =
= 2·105, то a » 123·105; если b = 1,2345, D(b) = 0,05, то b » 1,23).
Примеры.
1. Найти разность чисел: a * = 1,24 ± 0,03 и b * = 7,361 ± 0,007.
Решение. Погрешность: D(a – b) = D(a) + D(b) = 0,037 » 0,04 (формула (1)).
Результат вычитания: a – b = (1,24 – 7,361) ± 0,04 » – 6,12 ± 0,04.
2. Найти отношение чисел: х = 0,255 и у = 34,01, если известна погрешность d (х) = 1%.
Решение. Приближенное число у записано без указания его погрешности, следовательно, D(у) = 0,01, откуда находим: d (у) = 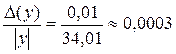 .
.
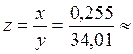 0,007498,
0,007498,
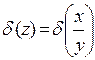 ={формула (3)}= d (х) + d (у) = 0,01 + 0,0003 = 0,0103 » 0,01,
={формула (3)}= d (х) + d (у) = 0,01 + 0,0003 = 0,0103 » 0,01,
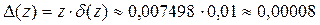 .
.
Результат деления: 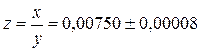 .
.
Если значение аргумента функции y = f (x) – приближенное число х, то абсолютную погрешность значения функции оценивают по следующей формуле:
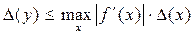 , где максимум модуля производной вычисляется как его наибольшее значение на промежутке
, где максимум модуля производной вычисляется как его наибольшее значение на промежутке 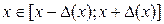 .
.
Абсолютную погрешность значения функции 2-х аргументов z = f (x, y) можно оценить по формуле:
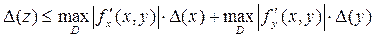 , (4)
, (4)
где максимум модулей частных производных находят среди всех их значений в области
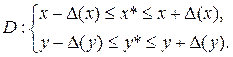
Аналогично определяется абсолютная погрешность значения функции трёх и более переменных.
Математика
Часть 6
Задания контрольной работы по теме «Численные методы»
и методические указания к ее выполнению
для студентов 2 курса вечерне-заочного факультета
всех специальностей
Контрольная работа №9
Мурманск
2008 г.
УДК 519.06 (076.5)
ББК 22.193 я 73
3 15
Составитель: Мостовская Любовь Григорьевна, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ
Методические рекомендации рассмотрены и одобрены кафедрой ВМ и ПО ЭВМ 05 декабря 2007 г., протокол № 4
Рецензент: Середа А.-В.И., канд. физ.-мат. наук, заведующий кафедрой ВМ и ПО ЭВМ
ÓМурманский государственный технический университет, 2008
Оглавление
Стр.
Введение. 4
Задания на контрольную работу по теме «Численные методы». 5
Содержание теоретического материала и ссылки на литературу.. 8
Справочный материал к выполнению контрольной работы 9
1. Погрешности вычислений. 9
1.1. Абсолютная и относительная погрешности. 9
1.2. Вычисления с учетом погрешностей. 11
2. Решение нелинейных уравнений. 12
2.1. Изоляция корней. 12
2.2. Уточнение корней уравнения методом деления отрезка пополам. 13
3. Решение систем линейных алгебраических уравнений. 15
3.1. Системы линейных алгебраических уравнений. 15
3.2. Решение систем линейных уравнений методом Гаусса. 16
3.3. Вычисление определителя матрицы с использованием метода Гаусса. 17
4. Интерполяционный многочлен в форме Лагранжа и его использование 18
5. Численное интегрирование функции одной переменной. 20
5.1. Квадратурные формулы.. 20
5.2. Квадратурная формула Симпсона. 20
6. Решение обыкновенных дифференциальных уравнений 1-го порядка методом Рунге-Кутты.. 21
7. Решение дифференциальных уравнений с частными производными. 22
7.1. Линейные дифференциальные уравнения 2-го порядка с частными производными. 22
7.2. Решение уравнения теплопроводности методом сеток. 24
Решение примерного варианта контрольной работы.. 26
Рекомендуемая литература.. 38
Введение
Настоящее пособие предназначено для студентов 2 курса вечерне-заочного факультета, обучающихся по техническим специальностям в МГТУ. В пособии содержатся ссылки на теоретический материал по теме «Численные методы», а также список рекомендуемой литературы и задания к выполнению контрольной работы. В результате изучения темы «Численные методы» студенты должны:
• знать основные правила вычисления приближенных значений величин;
• уметь оценивать погрешность полученного результата;
• знать основные методы решения нелинейных уравнений;
• уметь решать системы линейных алгебраических уравнений;
• знать основы интерполирования функций, заданных таблично;
• иметь представление об основных методах численного интегрирования и уметь использовать квадратурные формулы на практике;
• знать численные методы решения обыкновенных дифференциальных уравнений и иметь навыки их использования;
• иметь представление о численных методах решения дифференциальных уравнений с частными производными (уравнений математической физики).
Данные методические рекомендации включают справочный материал, необходимый для выполнения контрольной работы по теме «Численные методы», и решение примерного варианта работы, в котором имеются ссылки на используемый справочный материал.
Задания на контрольную работу по теме «Численные методы»
Контрольная работа состоит из семи задач. Задание для каждой задачи включает в себя ее формулировку и десять вариантов исходных данных.
Перед выполнением контрольной работы необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии со ссылками на литературу, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы.
Задача 1. Даны приближенные значения величин x и y и известно, что абсолютная погрешность D(х) = N /50, а относительная погрешность d (у) = N% (здесь и далее N – номер варианта). Требуется:
1) вычислить значение величины 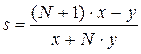 , оценить предельную абсолютную погрешность D(s) и округлить значение s в соответствии с погрешностью;
, оценить предельную абсолютную погрешность D(s) и округлить значение s в соответствии с погрешностью;
2) вычислить приближенное значение функции f (x, y) = ln(x + N)∙(N + y2),
оценить предельную абсолютную погрешность значения функции и округлить его в соответствии с погрешностью.
| Номер варианта | Значения величин x и y | Номер варианта | Значения величин x и y |
| 1 | x = 3,5; y = 0,48 | 2 | x = 4,1; y = 0,29 |
| 3 | x = 2,6; y = 0,54 | 4 | x = 1,4; y = 0,75 |
| 5 | x = 1,7; y = 0,42 | 6 | x = 6,5; y = 0,22 |
| 7 | x = 5,2; y = 0,35 | 8 | x = 3,8; y = 0,72 |
| 9 | x = 2,3; y = 0,62 | 10 | x = 5,9; y = 0,36 |
Задача 2. Дано уравнение N · x3 + x – N/3 = 0 (N – номер варианта). Требуется:
1) определить число корней уравнения и найти промежутки их изоляции;
2) вычислить значение одного из корней уравнения с точностью ε = 0,01 при помощи метода деления отрезка пополам.
Указание. Все промежуточные вычисления производить, используя не менее 4-х десятичных знаков после запятой.
Задача 3. Дана система линейных алгебраических уравнений:
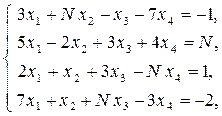 где N – номер варианта.
где N – номер варианта.
Требуется:
1) решить систему методом Гаусса;
2) вычислить определитель матрицы системы, используя метод Гаусса.
Указания. При решении системы использовать расширенную матрицу. Все промежуточные вычисления производить, используя не менее 4-х десятичных знаков после запятой. Округлить значения полученного решения x1, x2, x3, x4 до 2-x десятичных знаков после запятой.
Задача 4. Дана таблица значений функции f (x):
| xi | N – 0,7 | N – 0,3 | N + 0,1 | N + 0,5 | N + 0,9 |
| f (xi) | N/3 | N/6 | N/7 | N/5 | N/2 |
(N – номер варианта).
Требуется:
1) по табличным данным построить для функции f (x) интерполяционный полином 4-го порядка в форме Лагранжа и привести его к стандартному виду целого многочлена;
2) используя полученный полином, вычислить приближенное значение функции f (x) в точке 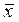 = N + 0,3.
= N + 0,3.
Указания Все вычисления производить, используя не менее 4-х десятичных знаков после запятой. Округлить полученное значение f ( 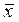 ) до 3-x десятичных знаков после запятой
) до 3-x десятичных знаков после запятой
Задача 5. Дан определенный интеграл 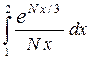 , где N – номер варианта. Требуется: составить таблицу значений подынтегральной функции в точках
, где N – номер варианта. Требуется: составить таблицу значений подынтегральной функции в точках
xi = 1 + ih, где i = 0, 1, …,10 с шагом h = 0,1 и вычислить приближенное значение интеграла, используя эту таблицу и формулу Симпсона.
Указание. Все вычисления производить, используя не менее 4-х десятичных знаков после запятой, полученный результат округлить до 3-х десятичных знаков после запятой.
Задача 6 . Дана задача Коши для обыкновенного дифференциального уравнения: y′ = Nx – y2, y(0) = N/10 (N – номер варианта). Решить задачу при помощи метода Рунге-Кутты на промежутке [0; 0,5] с шагом h = 0,1.
Указание. Все вычисления производить, используя не менее 4-х десятичных знаков после запятой.
Задача 7 . Температура однородного стержня U = U (х, t) в сечении х в момент времени t удовлетворяет уравнению теплопроводности. Используя метод сеток, найти решение смешанной задачи для уравнения теплопроводности 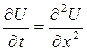 в области
в области 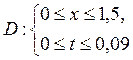 при заданных условиях: начальное распределение температуры в стержне U (х, 0) = f (x), температура на концах стержня U (0; t) = α (t), U (1,5; t) = β (t), где f (x), α (t), β (t) – заданные функции.
при заданных условиях: начальное распределение температуры в стержне U (х, 0) = f (x), температура на концах стержня U (0; t) = α (t), U (1,5; t) = β (t), где f (x), α (t), β (t) – заданные функции.
Указания. Для решения использовать сетку с шагом h = 0,3 по переменной х и с шагом d = 0,015 по переменной t. Все значения функции в узлах сетки вычислять с округлением до 4-го знака после запятой.
| Номер варианта | Функция f (x) | Функция α (t) | Функция β (t) |
| 1 | f (x) = 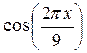
| α (t) = 1 – t2 | β (t) = 0,5 |
| 2 | f (x) = sin х | α (t) = 2 t | β (t) = cos 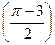
|
| 3 | f (x) = ln (х + 1) | α (t) = t2 | β (t) = ln (2,5) |
| 4 | f (x) = 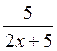
| α (t) = cos t | β (t) = 0,625 |
| 5 | f (x) = x2 + 2х | α (t) = sin t | β (t) = 5,25 |
| 6 | f (x) = 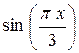
| α (t) = t2 + t | β (t) = 1 |
| 7 | f (x) = 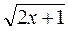
| α (t) = t2 + 1 | β (t) = 2 |
| 8 | f (x) = ln (4 – 2х) | α (t) = ln (t + 4) | β (t) = 0 |
| 9 | f (x) = 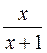
| α (t) = 3 t | β (t) = 0,6 |
| 10 | f (x) = 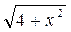
| α (t) = 2cos t | β (t) = 2,5 |
Содержание теоретического материала и ссылки на литературу
| № задачи | Содержание (темы) | Литература |
| 1 | Погрешности вычислений. Предельная абсолютная погрешность и предельная относительная погрешности вычислений. Вычисление приближенных значений функции | [1], гл. 1, §1; [2], гл. 1.1; [4], гл. I, работа №1(1), 2(2); [5], §1, 2.1, 2.2.1 |
| 2 | Методы решения нелинейных уравнений. Метод деления отрезка пополам | [1], гл. 4, §26; [2], гл.5.1, 5.2; [3], гл.IX, № 1168, 1169, 1170, 1178, 1179; [4], гл. IV, работа №1(15); [5], §2 |
| 3 | Численные методы решения систем линейных алгебраических уравнений. Метод Гаусса. Вычисление определителя с использованием метода Гаусса | [1], гл.3, §19; [2], гл. 2.1, 2.2; [4], гл. III, работа №2(7), 3(8); [5], §4.1.1, 6.1, |
| 4 | Полиномиальная интерполяция функций. Интерполяционный полином в форме Лагранжа и его использование | [1], гл. 1, §4, 5; [2], гл. 8.1, 8.2; [3], гл.IX, № 1192-1196; [4], гл. VI, работа №1(32) |
| 5 | Квадратурные формулы численного интегрирования. Формула Симпсона | [1], гл. 2, §15; [2], гл. 12.1, 12.3; [3], гл.IX, № 1205-1207; [4], гл. VII, работа №2(39) |
| 6 | Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений. Метод Рунге - Кутты | [1], гл. 2, §18; [2], гл. 14.1, 14.5, 14.6; [3], гл.IX, № 1234-1237; [4], гл. VIII, работа №2(43) |
| 7 | Понятие о методе сеток. Использование метода сеток для решения уравнений математической физики | [1], гл. 6, §31; [2], гл. 17.3, 19.1, 19.2, 20.1, 20.2; [4], гл. IX, работа №2(48) |
Примечание. Ссылки на литературу в таблице даны в соответствии с номерами в списке рекомендуемой литературы.
Справочный материал к выполнению контрольной работы
Погрешности вычислений
1.1. Абсолютная и относительная погрешности
Практические вычисления проводятся над числами, которые могут быть заданы не только точно, но и приближенно. Например, число 1/3 можно записать в виде десятичной дроби только приближенно.
Правило округления чисел: если первая из отбрасываемых цифр меньше пяти, то все сохраняемые цифры не изменяются, а если первая отбрасываемая цифра больше или равна пяти, то последняя сохраняемая цифра увеличивается на единицу.
Примеры. 13523 » 13500 = 135·102, 2,1564 » 2,16, – 0,325 » –0,33.
Обозначим 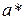 – точное значение некоторой величины, a – приближенное значение этой величины (приближенное число).
– точное значение некоторой величины, a – приближенное значение этой величины (приближенное число).
Величину 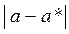 называют абсолютной погрешностью числа a.
называют абсолютной погрешностью числа a.
В большинстве случаев 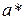 неизвестно, однако, можно указать некоторое число D(a), оценивающее абсолютную погрешность приближенного числа, т.е. удовлетворяющее условию
неизвестно, однако, можно указать некоторое число D(a), оценивающее абсолютную погрешность приближенного числа, т.е. удовлетворяющее условию 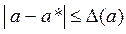 . Число D(a) называют предельной абсолютной погрешностью числа a. Обычно предельную абсолютную погрешность называют просто абсолютной погрешностью и записывают так:
. Число D(a) называют предельной абсолютной погрешностью числа a. Обычно предельную абсолютную погрешность называют просто абсолютной погрешностью и записывают так: 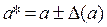 , причем в числах a и D(a) сохраняют одинаковое число знаков после запятой. При округлении предельной абсолютной погрешности его значение всегда берется «с избытком», т.е. последняя сохраняемая цифра увеличивается на единицу.
, причем в числах a и D(a) сохраняют одинаковое число знаков после запятой. При округлении предельной абсолютной погрешности его значение всегда берется «с избытком», т.е. последняя сохраняемая цифра увеличивается на единицу.
Примеры. 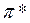 = 3,1416 ± 0,0001;
= 3,1416 ± 0,0001; 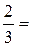 0, 67 ± 0,01.
0, 67 ± 0,01.
Предельной относительной погрешностью числа a называют величину 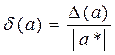 или
или 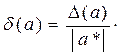 100%. В случае, когда
100%. В случае, когда 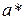 неизвестно, полагают, что d (a) =
неизвестно, полагают, что d (a) = 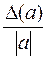 или d (a) =
или d (a) = 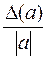 ·100%. Обычно предельную относительную погрешность числа называют просто относительной погрешностью.
·100%. Обычно предельную относительную погрешность числа называют просто относительной погрешностью.
Примеры. 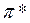 = 3,1416 ± 0,0001
= 3,1416 ± 0,0001 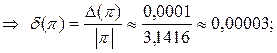
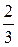 = а* = 0, 67 ± 0,01
= а* = 0, 67 ± 0,01 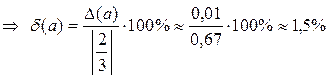 .
.
Первая слева цифра числа, отличная от нуля, и все цифры, расположенные правее нее, называются значащими цифрами числа. В записи погрешностей обычно оставляют одну значащую цифру, например, D(a) = 4·105, D(b) = 0,05, или d (х) = 3%.
Если приближенное число записано без указания его погрешности, то по умолчанию считается, что его абсолютная погрешность не превосходит единицы последнего сохраненного разряда в записи числа, например, запись
а » 2,320 означает, что D(a) = 0,001.
1.2. Вычисления с учетом погрешностей
При выполнении действий над приближенными числами происходит накопление погрешностей, и полученный результат не может быть точнее исходных данных.
Основные формулы для вычисления погрешностей арифметических операций:
D(с*·a) = с*·D(a), если с* – точное число (константа);
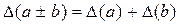 ; (1)
; (1)
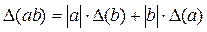 ;
;
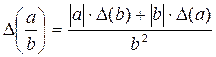 ; (2)
; (2)
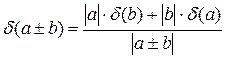 ;
;
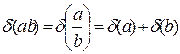 . (3)
. (3)
При выполнении арифметических операций обычно все промежуточные вычисления осуществляют с одной или двумя запасными десятичными цифрами по сравнению с желаемым результатом, а затем полученный результат округляют: либо до требуемой в задаче точности, либо в соответствии абсолютной погрешностью результата (например, если a = 12305362, D(a) =
= 2·105, то a » 123·105; если b = 1,2345, D(b) = 0,05, то b » 1,23).
Примеры.
1. Найти разность чисел: a * = 1,24 ± 0,03 и b * = 7,361 ± 0,007.
Решение. Погрешность: D(a – b) = D(a) + D(b) = 0,037 » 0,04 (формула (1)).
Результат вычитания: a – b = (1,24 – 7,361) ± 0,04 » – 6,12 ± 0,04.
2. Найти отношение чисел: х = 0,255 и у = 34,01, если известна погрешность d (х) = 1%.
Решение. Приближенное число у записано без указания его погрешности, следовательно, D(у) = 0,01, откуда находим: d (у) = 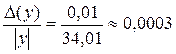 .
.
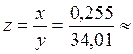 0,007498,
0,007498,
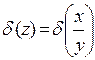 ={формула (3)}= d (х) + d (у) = 0,01 + 0,0003 = 0,0103 » 0,01,
={формула (3)}= d (х) + d (у) = 0,01 + 0,0003 = 0,0103 » 0,01,
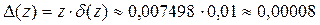 .
.
Результат деления: 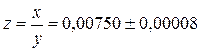 .
.
Если значение аргумента функции y = f (x) – приближенное число х, то абсолютную погрешность значения функции оценивают по следующей формуле:
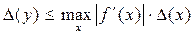 , где максимум модуля производной вычисляется как его наибольшее значение на промежутке
, где максимум модуля производной вычисляется как его наибольшее значение на промежутке 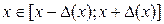 .
.
Абсолютную погрешность значения функции 2-х аргументов z = f (x, y) можно оценить по формуле:
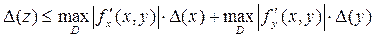 , (4)
, (4)
где максимум модулей частных производных находят среди всех их значений в области
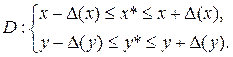
Аналогично определяется абсолютная погрешность значения функции трёх и более переменных.
Решение нелинейных уравнений
2.1. Изоляция корней
Пусть требуется найти корни (решения) уравнения
f (x) = 0 (5),
где f (x) – нелинейная функция.
В общем случае можно говорить лишь о приближенном вычислении корней уравнения (5), т.е. о получении такого значения аргумента, при котором f (x) » 0. Принято считать, что точное решение x * этого уравнения получено с точностью ε, если для полученного приближенного решения x выполнено условие 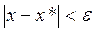 .
.
Если непрерывная функция f (x) является знакопеременной в области определения, то уравнение (5) имеет конечное или бесконечное количество корней. Каждый из корней получают, используя численные методы, после процедуры отделения корней.
Отделить корень уравнения (5) – значит найти такой интервал (a, b), в котором содержится корень уравнения, причем только один.
Известно, что если на концах некоторого промежутка [a, b] непрерывная функция f (x) имеет разные знаки, т.е. 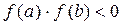 , а внутри этого промежутка производная
, а внутри этого промежутка производная 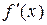 знак не меняет, то в интервале (a, b) существует корень уравнения (5), причем только один.
знак не меняет, то в интервале (a, b) существует корень уравнения (5), причем только один.
Процедура отделения корней может быть осуществлена графически (построением графика функции f (x)) или с помощью проверки знака функции на некотором множестве значений x, например, на множестве равноотстоящих точек на оси абсцисс.
2.2. Уточнение корней уравнения методом деления отрезка пополам
Пусть требуется решить уравнение (5) с заданной точностью ε. Известен промежуток изоляции корня x * – промежуток [a, b], на концах которого непрерывная функция f (x) имеет разные знаки, а внутри этого промежутка производная 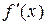 знак не меняет.
знак не меняет.
Процедура уточнения корня заключается в построении последовательности точек x0, x1, x2, ….. xk,…., такой, что 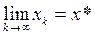 . Процесс вычисления заканчивается, когда получено xk, удовлетворяющее условию
. Процесс вычисления заканчивается, когда получено xk, удовлетворяющее условию
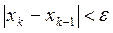 . (6)
. (6)
Опишем метод уточнения корня, называемый методом деления отрезка пополам, или методом дихотомии, или методом бисекции. Иногда этот метод называют еще методом проб.
Уточнение корня методом деления отрезка пополам осуществляется в следующем порядке:
1) вводим обозначении: а0 = a, b0 = b;
2) вычисляем 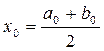 ;
;
3) из двух интервалов (а0, x0) и (x0, b0) выбираем тот, на концах которого f (x) имеет разные знаки, и обозначаем концы этого интервала a1, b1;
4) вычисляем 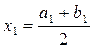 ;
;
5) из двух интервалов (а1, x1) и (x1, b1) выбираем тот, на концах которого f (x) имеет разные знаки, и обозначаем концы этого интервала a2, b2;
6) вычисляем  ,
,
и так далее, пока не будет выполнено условие 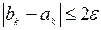 , – тогда приближенное значение корня
, – тогда приближенное значение корня 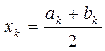 будет удовлетворять условию (6), т.е. решением уравнения будет число
будет удовлетворять условию (6), т.е. решением уравнения будет число 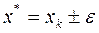 .
.
Последовательность {xk}, полученная методом деления отрезка пополам, сходится к точному решению х*, если функция f (x) непрерывна на [a, b].
Описание алгоритма метода.
1. Для k = 0 выполняем:
 . (7)
. (7)
2. Увеличиваем номер шага k := k + 1, выполняем вычисления:
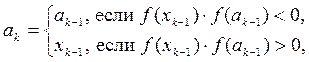 (8.1)
(8.1)
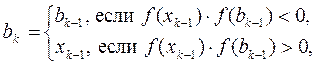 (8.2)
(8.2)
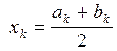 . (8.3)
. (8.3)
3. Проверяем условие
 . (9)
. (9)
Если условие не выполняется, переходим к пункту 2, если условие выполняется, то процесс закончен. Получаем ответ: 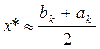 .
.
Дата: 2018-12-28, просмотров: 401.