3.1. Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений (СЛАУ) – это система уравнений вида:

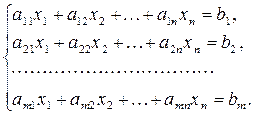
Здесь x₁, x₂, ….., x_n – неизвестные величины, a_ij, b_j  – заданные коэффициенты (i = 1, 2,…,m;  j = 1, 2, ….,n).

Решение системы – это такой набор чисел x₁*, x₂*, ….., x_n *, при подстановке которых во все уравнения системы уравнения становятся тождествами.

СЛАУ называется совместной, если у нее есть хотя бы одно решение, и несовместной, если ни одного решения у нее нет. СЛАУ называется определенной, если у нее есть решение и притом только одно.

Рассмотрим систему n уравнений с n неизвестными (m = n). Если обозначить матрицы:

;        ,

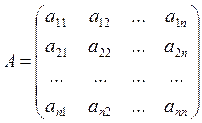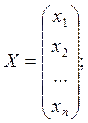
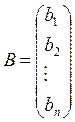то получим матричную форму СЛАУ: AX = В. Матрица А называется матрицей системы, матрица-столбец  В – столбцом свободных членов, а  Х – столбцом  неизвестных.

Требуется найти решение системы – столбец .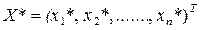

Известно, что если матрица системы А – невырожденная (ее определитель не равен нулю), то система имеет единственное решение. Точное решение системы Х* удается получить только для небольших размерностей n, если производить все вычисления без округлений (в простых дробях). В реальных задачах чаще получается приближенное решение системы.

3.2. Решение систем линейных уравнений методом Гаусса

Метод Гаусса решения СЛАУ – это метод исключения неизвестных. Решение методом Гаусса осуществляется в два этапа, которые называются «прямой ход» и «обратный ход».

На k-м шаге прямого хода (k = 1,…,n–1) осуществляется выбор ведущей строки и ведущего элемента, затем исключение неизвестной x_k из уравнений с номерами i > k. В результате прямого хода за (n –1) шагов матрица А приводится к верхнему треугольному виду и система приобретает вид:

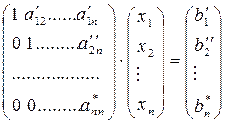
После этого легко найти неизвестные x_n, x_n-1,….,x₁  (обратный ход).

Различные схемы реализации метода Гаусса отличаются способом выбора ведущего элемента. Опишем одну из этих схем – схему единственного деления.

Для удобства вычислений будем использовать расширенную матрицу A |В, у которой первые n столбцов совпадают с матрицей А, а (n+1)-й столбец – это столбец В свободных членов системы:

.

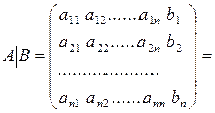
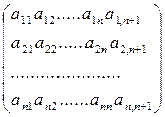Описание алгоритма метода.

Прямой ход. На каждом из шагов с номерами k = 1, …, n –1 выполняем следующие операции.

1) выбираем ведущую строку с номером k, ведущий элемент a_kk, и все элементы ведущей строки расширенной матрицы делим на число d_k = a_kk:

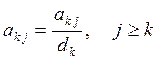;                             (10)

2) из каждой строки расширенной матрицы с номером i > k вычитаем ведущую строку, умноженную на число с _ik = a_ik, получая нули под ведущим элементом:

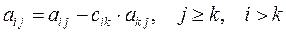;                       (11)

3) если  k = n – 1, то прямой ход закончен, а если нет, то увеличиваем номер шага и ведущей строки: k := k +1 и повторяем шаги 1), 2).

В результате прямого хода за (n–1) шагов система приводится к верхнему треугольному виду, например, система 4-го порядка приводится к виду:

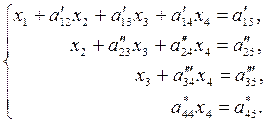
Полученная система эквивалентна исходной системе, т.е. имеет то же самое решение.

Обратный ход.  По формулам

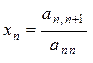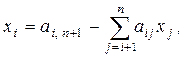;    i = n –1, n –2,…,1 (12)

находим решение системы x₁, x₂, ….., x_n.

Схема единственного деления реализации метода Гаусса может быть использована только в том случае, когда ведущие элементы всех шагов отличны от нуля.

3.3. Вычисление определителя матрицы с использованием метода Гаусса

     При решении системы n линейных алгебраических уравнений с n неизвестными методом Гаусса (n – 1) раз производится деление ведущей строки на ведущий элемент, при этом определитель матрицы системы тоже делится на это число. После приведения системы к верхнему треугольному виду определитель матрицы полученной системы равен произведению элементов главной диагонали: 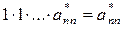. Если все ведущие элементы были отличны от нуля, тогда определитель матрицы исходной системы равен произведению всех ведущих элементов на число :

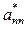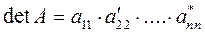                      (13)